Using Radial Distribution Function to Analyze Atomic Structure from MD: A Comprehensive Guide for Biomedical Research

Abstract

This article provides a comprehensive guide for researchers and drug development professionals on utilizing the Radial Distribution Function (RDF) to extract critical structural insights from Molecular Dynamics (MD) simulations. It covers the fundamental theory of RDF, practical implementation methods using popular software tools, optimization techniques for enhanced performance, and validation approaches against experimental data. The content explores applications in characterizing biomolecular interactions, solvation shells, and drug-binding sites, with specific examples from cancer research involving EGFR and H-Ras proteins. This resource bridges computational analysis with experimental validation, offering practical strategies for advancing drug discovery and materials design.

Understanding Radial Distribution Functions: From Basic Theory to Molecular Insights

What is the RDF? Defining the Fundamental Concept and Mathematical Formulation

The Radial Distribution Function (RDF), denoted as ( g(r) ), is a fundamental concept in statistical mechanics that describes the probability of finding a particle at a distance ( r ) from a reference particle in a homogeneous and isotropic system [1]. It serves as a powerful tool for characterizing the atomic and molecular structure of materials, providing a quantitative measure of how particle density varies with distance from a reference point [2] [3]. By revealing the spatial arrangement of particles, the RDF provides crucial insights into the structure of various condensed matter systems, including ordered crystals, disordered materials, and liquids, making it one of the most effective tools for characterizing the nature and structure of substances, particularly fluids and fluid mixtures [1].

The significance of the RDF extends beyond structural description, as it forms a critical bridge between microscopic interactions and macroscopic thermodynamic properties [1]. This function enables researchers to connect the arrangements and interactions of individual atoms or molecules with bulk material properties that can be measured experimentally. Knowledge of the RDF is crucial for multiple reasons: it bridges macroscopic thermodynamic properties with interparticle interactions; it plays a crucial role in fluctuation theory; and it provides a clear view of particle correlations and how these interactions decay with distance [1]. In the context of molecular dynamics (MD) research, the RDF serves as an essential analytical tool for validating simulations against experimental data and for understanding the structural features of complex molecular systems at the atomic level [4].

Mathematical Formulation

Fundamental Definition

The radial distribution function is mathematically defined for a system of ( N ) particles in volume ( V ) at temperature ( T ) as follows. For particles of types ( a ) and ( b ), the RDF ( g_{ab}(r) ) is given by:

[ g{ab}(r) = \frac{1}{N{a}} \frac{1}{N{b}/V} \sum{i=1}^{Na} \sum{j=1}^{Nb} \langle \delta(|\mathbf{r}i - \mathbf{r}_j| - r) \rangle ]

which is normalized so that the RDF becomes 1 for large separations in a homogeneous system [5]. The RDF effectively counts the average number of ( b ) neighbours in a shell at distance ( r ) around an ( a ) particle and represents it as a density [5].

In the canonical ensemble (( N,V,T )), the RDF can be expressed through the generalized expression:

[ g^{(n)}(\mathbf{r}1, \ldots, \mathbf{r}n) = \frac{V^{N}}{N!} \left( \prod{i=n+1}^{N} \frac{1}{V} \int \mathrm{d}^3 \mathbf{r}i \right) \frac{1}{ZN} \sum{\pi \in SN} e^{-\beta U(\mathbf{r}{\pi(1)}, \ldots, \mathbf{r}_{\pi(N)})} ]

where ( Z_N ) is the configurational integral, ( \beta = 1/kT ), and ( U ) is the potential energy function [2].

Key Mathematical Relationships

From the radial distribution function, several important related functions can be derived. The radial cumulative distribution function is defined as:

[ G{ab}(r) = \int0^r !!dr' 4\pi r'^2 g_{ab}(r') ]

and the average number of ( b ) particles within radius ( r ) is:

[ N{ab}(r) = \rho G{ab}(r) ]

where ( \rho ) is the appropriate number density [5]. The latter function is particularly useful for computing coordination numbers, such as the number of neighbors in the first solvation shell, where the upper limit ( r_1 ) is typically taken as the position of the first minimum in ( g(r) ) [5].

In practice, for molecular dynamics simulations, the continuous function ( p(r) ) is replaced with a histogram on a grid:

[ p(r) = \frac{1}{N{\text{frame}}} \sumi^{N{\text{frame}}} \sum{j \in \text{sel1}} \sum{k \in \text{sel2}; k \neq j} \sum{\text{all } \kappa} d{\kappa}(r; r{ijk}) ]

where ( N{\text{frame}} ) is the number of frames, ( r{ijk} ) is the distance between atom ( j ) and atom ( k ) for frame ( i ), and ( d{\kappa} ) is a function that is ( 1/\Delta r ) if ( r{\kappa} \leq r \leq r{\kappa} + \Delta r ) and ( r{\kappa} \leq r{ijk} \leq r{\kappa} + \Delta r ), and 0 otherwise [4].

Table 1: Key Mathematical Functions in RDF Analysis

Function	Mathematical Expression	Physical Interpretation
Radial Distribution Function ( g(r) )	( g{ab}(r) = \frac{1}{Na} \frac{1}{Nb/V} \sum{i=1}^{Na} \sum{j=1}^{N_b} \langle \delta(	\mathbf{r}i - \mathbf{r}j	- r) \rangle )	Probability density of finding particle b at distance r from particle a
Cumulative Distribution ( G(r) )	( G{ab}(r) = \int0^r dr' 4\pi r'^2 g_{ab}(r') )	Integrated probability within radius r
Coordination Number ( N(r) )	( N{ab}(r) = \rho G{ab}(r) )	Average number of b particles within radius r of a

Computation from Molecular Dynamics Trajectories

Core Algorithm and Workflow

The calculation of radial distribution functions from molecular dynamics trajectory data involves a computationally expensive analysis task where the rate-limiting step is building a histogram of the distances between atom pairs in each trajectory frame [4]. The general algorithm involves:

• Selection of atom pairs from the groups of interest
• Distance calculation between all relevant atom pairs, accounting for periodic boundary conditions via the minimum image convention
• Histogram accumulation of these distances across multiple simulation frames
• Normalization of the histogram by the expected density of an ideal gas

The probability distribution ( p(r) ) is calculated as an average over a thermodynamic ensemble. In MD simulations, frames are chosen from trajectories sampling the thermodynamic ensemble of interest:

[ p(r) = \frac{1}{N{\text{frame}}} \sumi^{N{\text{frame}}} \sum{j \in \text{sel1}} \sum{k \in \text{sel2}; k \neq j} \delta(r - r{ijk}) ]

where ( \delta ) is the Dirac delta function, replaced in practice by a histogram binning function [4].

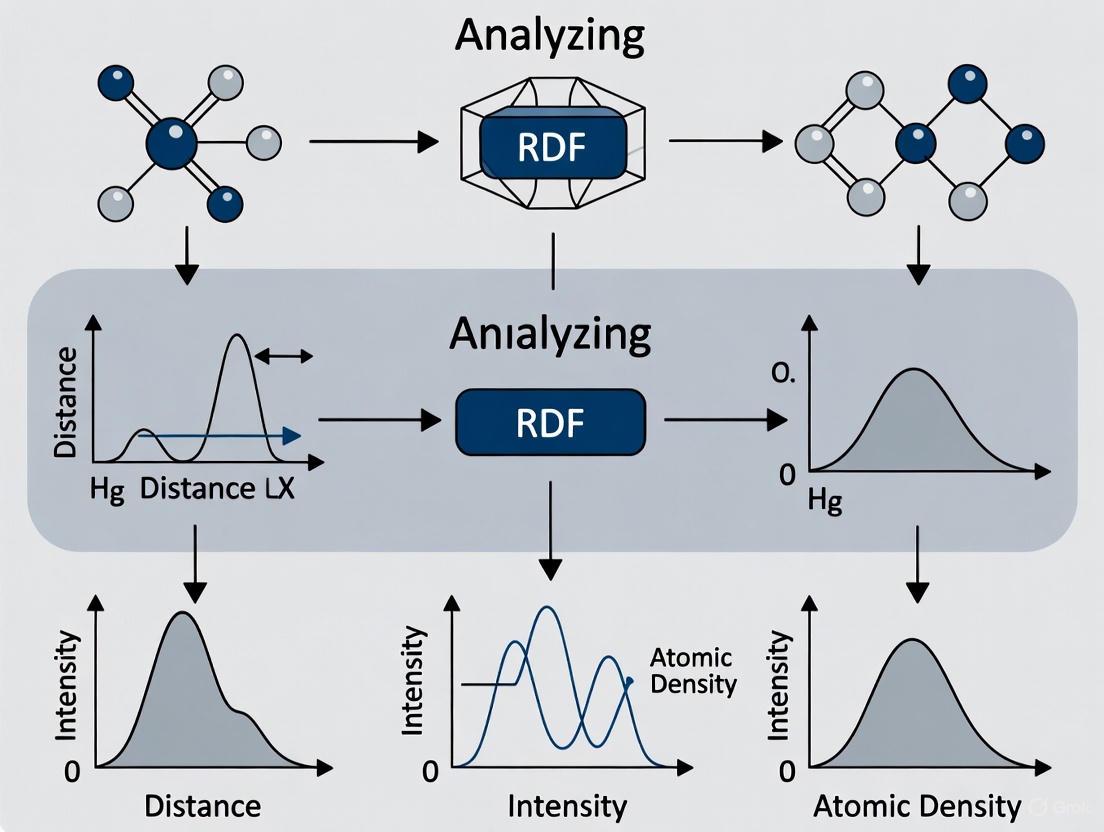
RDF Computation Workflow: Diagram illustrating the key steps in calculating radial distribution functions from molecular dynamics trajectories.

Accounting for Periodic Boundary Conditions

A critical aspect of RDF calculation in MD simulations is proper handling of periodic boundary conditions (PBC). Assuming the upper bound of the histogram is less than or equal to half the width of the periodic box, the distance ( r_{ijk} ) is calculated as the distance between atom ( j ) and the closest periodic image of atom ( k ) [4]. For example, the magnitude of the x-component of the shortest vector connecting atom ( j ) to a periodic image of atom ( k ) is given by:

[ |x{ijk}| = \begin{cases} |xk - xj| & \text{if } |xk - xj| \leq a/2 \ a - |xk - x_j| & \text{otherwise} \end{cases} ]

where ( xj ) and ( xk ) are the x-coordinates of atoms ( j ) and ( k ), and ( a ) is the length of the periodic box in the x-direction [4]. Similar calculations are performed for the y and z components, with the minimum distance then computed using the standard Euclidean formula.

Advanced Computational Implementations

Due to the computational expense of RDF calculations for large systems (O(N²) complexity), significant effort has been dedicated to optimizing these algorithms. State-of-the-art implementations leverage:

• Graphics Processing Units (GPUs): Modern implementations utilize massive parallelism on GPUs, with specialized tiling schemes to maximize data reuse at the fastest levels of the GPU memory hierarchy [4]. The use of atomic memory operations allows the fast, limited-capacity on-chip memory to be used more efficiently, resulting in significant performance increases compared to versions without atomic operations [4].

• Parallelization Strategies: Multi-GPU implementations with dynamic load balancing allow high performance on heterogeneous GPU configurations. One implementation running on four NVIDIA GeForce GTX 480 GPUs achieved a 92x speedup compared to a multithreaded CPU implementation [4].

• Specialized Software Tools: Packages like MDAnalysis, VMD, LAMMPS, and OVITO provide optimized RDF analysis capabilities. For example, MDAnalysis offers both averaged and site-specific RDF implementations with various normalization options and exclusion capabilities to avoid counting correlated atoms within the same molecule [5] [6] [7].

RDF Analysis in Materials and Drug Development

Interpretation of RDF Features

The radial distribution function provides distinct signatures that characterize different states of matter and specific atomic-level interactions:

• Liquids: Show decaying oscillatory behavior, with the first peak representing the first solvation shell, and subsequent peaks indicating higher-order coordination shells. The oscillations eventually dampen to a value of 1 at large distances, indicating no long-range order [3] [1].

• Crystalline Solids: Exhibit sharp, well-defined peaks that extend to large distances, reflecting the long-range periodic order of the crystal lattice [1].

• Gases: Display a single peak at small interatomic distances, with the RDF quickly approaching 1, reflecting the lack of structure in gaseous systems [3].

• Glasses and Disordered Materials: Show broad peaks that typically decay within a few atomic diameters, indicating short-range order but no long-range periodicity [8].

Table 2: Characteristic RDF Features for Different Material Phases

Material Phase	First Peak Characteristics	Long-Range Behavior	Coordination Number
Gas	Single broad peak at small r	Rapidly approaches g(r)=1	Low and poorly defined
Liquid	Sharp first peak, broader subsequent peaks	Oscillations decay to g(r)=1	Well-defined first shell
Amorphous Solid	Broadened peaks	Short-range order only (2-3 peaks)	Reasonably well-defined
Crystalline Solid	Sharp, narrow peaks	Long-range order (many peaks)	Precisely defined

Applications in Drug Development and Biomolecular Systems

RDF analysis plays a crucial role in understanding molecular interactions relevant to drug development, particularly in studying solvation effects, binding processes, and specific molecular recognition events:

• Solvation Studies: The RDF helps understand binding processes aided by solvent, providing insights into hydration shells around drug molecules and biomolecular targets [8]. Changes in RDF can indicate alterations in water-protein interactions, which are crucial for understanding ligand binding and biomolecular stability [8].

• Hydrogen Bonding Analysis: In biological systems, RDF offers quantitative insight into hydrogen-bonded systems such as proteins and DNA [1]. The first peak between hydrogen (donor) and acceptor atoms (O-H or N-H groups) typically appears at 1.5-2.5 Ã…, with the intensity of this peak providing information about hydrogen bond strength and stability [1].

• Protein-Ligand Interactions: Site-specific RDF analysis enables researchers to study solvation shells of ligands in binding sites or the solvation of specific residues in proteins [5] [6]. This provides atomic-level insights into interaction mechanisms and binding affinity.

• Coordination Analysis: RDF between specific atom types (e.g., Si and O in MCM-41 wall structure) clarifies coordination states and structural uniformity, with implications for drug delivery systems and catalytic applications [8].

Experimental Protocols and Methodologies

Computational Protocol Using MDAnalysis

The following protocol provides a detailed methodology for calculating radial distribution functions using the MDAnalysis library in Python:

For site-specific RDF analysis, where individual atomic contributions are of interest:

Advanced Protocol with Exclusion Rules

For complex molecular systems, proper exclusion of directly bonded atoms and atoms within the same molecule is crucial for meaningful RDF interpretation:

Table 3: Research Reagent Solutions for RDF Analysis

Tool/Software	Application Context	Key Functionality
MDAnalysis	Python library for MD analysis	Provides InterRDF and InterRDF_s classes for RDF calculations with various normalization options and exclusion rules [5] [6]
VMD with GPU acceleration	Visualization and analysis of MD trajectories	Implements highly optimized multi-GPU RDF algorithms for large systems (up to 1,000,000 atoms) [4]
LAMMPS	MD simulation package	Built-in RDF computation during simulation runs for various particle types [3]
OVITO	Visualization and analysis	User-friendly RDF calculation with graphical interface [3]
GROMACS	MD simulation package	g_rdf program for RDF analysis from trajectories, integrated with Xmgrace for plotting [8]

Relationship to Thermodynamic Properties and Advanced Applications

Connecting RDF to Macroscopic Properties

The radial distribution function serves as the fundamental link between microscopic structure and macroscopic thermodynamic properties. For a pure fluid, the RDF enables calculation of several key thermodynamic quantities:

• Internal Energy: The energy can be obtained from the integral of the pair potential weighted by the RDF: [ E = \frac{3}{2}NkT + 2\pi\rho \int_0^{\infty} u(r) g(r) r^2 dr ] where ( u(r) ) is the pair potential [1].

• Pressure: The equation of state follows from the virial theorem: [ P = \rho kT - \frac{2\pi\rho^2}{3} \int_0^{\infty} \frac{du(r)}{dr} g(r) r^3 dr ]

• Compressibility: The isothermal compressibility relates to long-wavelength density fluctuations: [ \rho kT \kappaT = 1 + 4\pi\rho \int0^{\infty} [g(r) - 1] r^2 dr ]

These relationships demonstrate how the RDF bridges atomic-level interactions with measurable bulk properties, making it invaluable for predicting material behavior from molecular simulations [1].

Specialized Applications in Drug Development

RDF analysis provides critical insights for rational drug design through several specialized applications:

• Hydration Shell Analysis: By calculating RDFs between drug molecules and water, researchers can characterize hydration patterns that influence solubility, permeability, and binding affinity. Changes in RDF peaks indicate alterations in water-drug interactions, which can be crucial for understanding formulation effects [8].

• Binding Site Solvation: Site-specific RDF analysis around binding pockets reveals water structure and displacement energetics, informing the design of ligands with optimal binding characteristics. The RDF between protein atoms and water molecules identifies tightly bound water molecules that may mediate protein-ligand interactions [5].

• Ion Coordination Studies: For ionizable drugs or metal-containing therapeutics, RDF analysis characterizes ion coordination environments and binding geometries, supporting the design of more effective metallodrugs and understanding their mechanism of action [8].

• Polymer-Based Drug Delivery: RDF analysis of polymer-drug systems reveals molecular-level interactions that control drug loading and release kinetics, guiding the design of improved delivery systems [1].

The radial distribution function thus represents a fundamental analytical tool that connects molecular-level structural details with macroscopic material properties and biological functions, making it an indispensable component of modern molecular dynamics research in materials science and drug development.

The Radial Distribution Function (RDF), denoted as (g_{AB}(r)), is a fundamental structural descriptor in molecular simulation that quantifies how the density of particle type (B) varies as a function of distance from particle type (A) [9]. In molecular dynamics (MD) research, the RDF provides crucial insights into the spatial arrangement of atoms, molecules, and ions within a system, serving as a bridge between microscopic configurations and macroscopic thermodynamic properties [10]. This application note details the interpretation of RDF features—specifically peaks, valleys, and their structural significance—within the context of analyzing atomic structures from MD simulations, with particular relevance for researchers in structural biology and drug development.

The RDF is formally defined in GROMACS through the equation: [ g{AB}(r) = \frac{\langle \rhoB(r) \rangle}{\langle\rhoB\rangle{local}} = \frac{1}{\langle\rhoB\rangle{local}}\frac{1}{NA} \sum{i \in A}^{NA} \sum{j \in B}^{NB} \frac{\delta( r{ij} - r )}{4 \pi r^2} ] where (\langle\rhoB(r)\rangle) represents the particle density of type (B) at distance (r) from particles (A), and (\langle\rhoB\rangle{local}) is the average particle density of type (B) over all spheres around particles (A) with radius (r{max}) [9]. In MDAnalysis, this is implemented with equivalent physical meaning, calculating the probability of finding particle (B) at distance (r) from particle (A) compared to an ideal gas [5] [11].

Quantitative Interpretation of RDF Features

Characteristic Features and Their Structural Significance

The RDF profile contains specific features—peaks, valleys, and their properties—that directly correlate with the system's structural properties. Table 1 summarizes the quantitative relationships between RDF features and their structural interpretations, particularly for Lennard-Jones fluids, which serve as important reference systems [10].

Table 1: Structural Interpretation of RDF Features in Lennard-Jones Fluids

RDF Feature	Structural Meaning	Quantitative Relationship	Physical Interpretation
First Peak Position ((r_{peak}))	Most probable distance to nearest neighbors	Shorter (r) with increasing temperature [10]	Indicates strong repulsive/attractive force balance
First Peak Height ((g_{peak}))	Probability of finding neighbors at (r_{peak})	(g{peak} = g{peak}(\rho^, \beta^)) [10]	Measures structural order/thermal motion
First Valley Position ((r_{valley}))	Boundary of first coordination shell	Integration limit for coordination number [10]	Defines nearest neighbor sphere
Coordination Number ((CN))	Number of nearest neighbors	(CN = \int0^{r{valley}} 4\pi\rho r^2 g(r) dr) [10]	Quantifies local packing density

For LJ fluids, empirical correlations connect RDF features to thermodynamic state variables. The height of the first peak follows: [ g{peak} = g{peak}(\rho^, \beta^) ] where (\rho^* = \rho\sigma^3) is the reduced density and (\beta^* = \epsilon/kBT) is the reduced inverse temperature [10]. Similarly, the position of the first peak (r{peak}^*) shows a deterministic relationship with the system's state point, enabling researchers to infer thermodynamic conditions from structural data alone [10].

Advanced Structural Descriptors Derived from RDF

Beyond the basic RDF, several derived quantities provide additional structural insights:

• Cumulative Distribution Function: (G{ab}(r) = \int0^r dr' 4\pi r'^2 g_{ab}(r')) provides the integral of the RDF up to distance (r) [5]
• Cumulative Coordination Number: (N{ab}(r) = \rho G{ab}(r)) gives the average number of (b) particles within radius (r) of an (a) particle [5]
• Angle-Dependent RDF: (g_{AB}(r,\theta)) extends structural analysis to anisotropic systems by incorporating orientation dependence [9]

The first minimum in the RDF ((r_1)) is particularly important as it defines the boundary of the first coordination shell, enabling calculation of coordination numbers for direct solvation analysis [5].

Experimental Protocols for RDF Analysis

Computational Methodology for RDF Calculation

The following protocol outlines the standard methodology for calculating and analyzing RDFs from molecular dynamics trajectories using modern analysis tools.

Figure 1: RDF Analysis Workflow from MD Trajectories

Protocol 1: RDF Calculation Using MDAnalysis

• System Preparation: Define atom groups for analysis

  • Select reference group (A) and target group (B)
  • Consider chemical specificity (e.g., oxygen-oxygen, protein-ligand atoms)

• Parameter Selection:

  • Set histogram bins (nbins=75 typically sufficient)
  • Define distance range (range=(0.0, 15.0) Ã… appropriate for most solvation shells)
  • Apply exclusion rules for bonded atoms (exclude_same="residue")

• Calculation Execution:

  [5]

• Normalization Method Selection:

  • Use norm='rdf' for standard (g_{ab}(r))
  • Use norm='density' for single particle density (n_{ab}(r))
  • Use norm='none' for raw particle counts [5]

Protocol 2: Site-Specific RDF Analysis

For detailed binding site analysis, particularly in drug discovery contexts:

• Identify Specific Interaction Sites:

  • Select ligand atoms and protein binding site residues
  • Define multiple pairs for site-specific analysis: ags = [[A1, B1], [A2, B2], ...]

• Execute Site-Specific Calculation:

  [5]

• Access Individual Site Results:

  • Results stored in rdf_s.results.rdf[i] for i-th atom pair
  • Access specific interactions: rdf_s.results.rdf[0][0, 0] for first atom in A1 with first atom in B1 [5]

RDF Analysis in Force Field Validation

RDF analysis plays a critical role in force field validation and development. Table 2 showcases the application of RDF analysis in validating the GROMOS 54A8 force field, demonstrating how structural comparisons inform parameter refinement [12].

Table 2: RDF Analysis in GROMOS 54A8 Force Field Validation

System Analyzed	RDF Application	Key Finding	Significance for Drug Development
Aqueous Electrolytes	Ion-ion vs ion-water RDFs	Good agreement for oligoatomic ions (acetate, methylammonium)	Improves accuracy of protein-ligand binding simulations
Protein Surface Residues	Solvation shell analysis	Charged residues more hydrated in 54A8 vs 54A7	Enh prediction of solvent-exposed binding sites
Salt Bridge Formation	Interionic distance distributions	Equivalent in 54A7 and 54A8 parameter sets	Maintains stability of protein-protein interactions

As demonstrated in GROMOS 54A8 validation, RDF analysis confirmed that "the side chains of arginine, lysine, aspartate, and glutamate residues appear slightly more hydrated and present a slight excess of oppositely-charged solution components in their vicinity" compared to its predecessor [12]. This precise structural insight is crucial for accurate prediction of binding affinities in drug design.

The Scientist's Toolkit: Essential Research Reagents and Computational Solutions

Table 3: Research Reagent Solutions for RDF Analysis

Tool/Solution	Function in RDF Analysis	Application Context
GROMACS gmx rdf	Calculates standard and angle-dependent RDFs	General biomolecular simulation analysis [9]
MDAnalysis InterRDF	Average RDF between two atom groups	Python-based analysis workflow [5]
MDAnalysis InterRDF_s	Site-specific RDF for detailed interactions	Ligand-binding site analysis [5] [11]
GROMOS 54A8 Force Field	Provides nonbonded parameters for charged groups	Accurate simulation of protein-ligand systems [12]
Lennard-Jones Reference Data	Empirical RDF-state point correlations [10]	Force field validation and calibration
Benzamil	Benzamil, CAS:2898-76-2, MF:C13H14ClN7O, MW:319.75 g/mol	Chemical Reagent
5-Iminodaunorubicin	5-Iminodaunorubicin, CAS:72983-78-9, MF:C27H30N2O9, MW:526.5 g/mol	Chemical Reagent

The precise interpretation of peaks, valleys, and structural features in radial distribution functions provides indispensable insights for molecular dynamics research in drug development. Through the protocols and quantitative relationships presented herein, researchers can extract meaningful structural information about solvation shells, binding sites, and molecular packing that directly informs therapeutic design. The integration of RDF analysis with modern force fields such as GROMOS 54A8 and computational tools like MDAnalysis creates a robust framework for advancing structural biology and rational drug design.

Connecting RDF to Thermodynamic Properties and System Energy

The radial distribution function (RDF), denoted as (g(r)), is a fundamental structural metric in statistical mechanics that describes how the density of particles varies as a function of distance from a reference particle [13] [2]. In the context of molecular dynamics (MD) simulations, which predict the trajectory of atoms over time based on a molecular mechanics force field [14] [15] [16], the RDF provides a bridge between the microscopic atomic structure of a system and its macroscopic thermodynamic properties [13] [2]. By statistically averaging the local particle density, the RDF reveals the short-range order and solvation shell structure in dense, disordered systems like liquids and solutions [13]. This structural information is critical because the thermodynamic state of a system is a direct consequence of the interactions and spatial arrangement of its constituent atoms [17] [16]. This article details the protocols and application notes for extracting thermodynamic properties and system energy from RDF analysis within MD research, with a particular focus on applications relevant to drug development, such as studying solvation and binding.

Theoretical Foundation: From Structure to Thermodynamics

Defining the Radial Distribution Function

The RDF, (g(r)), is defined as the ratio of the average local number density of particles at a distance (r), (\langle \rho (r) \rangle), to the bulk density of particles, (\rho) [13] [2]: [g(r) =\dfrac{\langle \rho (r) \rangle }{\rho}] In a typical dense fluid, (g(r)) is zero at the core (excluding the reference particle), rises to a peak at the distance of the first solvation shell, exhibits dampening oscillations at further distances, and finally approaches a value of 1, indicating a loss of correlation and a homogeneous fluid [13]. The probability of finding a particle in a spherical shell of thickness (dr) at distance (r) is given by (P(r) = 4 \pi r^{2} g(r) dr) [13].

Linking RDF to Energy and Thermodynamic Properties

The RDF provides a complete statistical description of the pair interactions in a system. This information can be used to compute several key thermodynamic properties, as the potential energy of the system is directly related to the interactions between particle pairs [2] [16]. The tables below summarize the core quantitative relationships.

Table 1: Fundamental RDF Definitions and Probability Measures

Concept	Mathematical Formula	Physical Interpretation
Radial Distribution Function	(g(r) = \dfrac{\langle \rho (r) \rangle }{\rho}) [13]	Measures the influence of a central particle on the local density of its neighbors.
Pair Correlation Function	(g{ab}(r)= \left \langle \rho{ab}(r)\right \rangle /\rho) [13]	The RDF between different types of particles 'a' and 'b'.
Probability Density	(P(r)=4 \pi r^{2} g(r)\ \mathrm{d} r) [13]	The probability of finding a particle at a distance (r) in a shell of thickness (dr).

Table 2: Key Thermodynamic Properties Derived from the RDF

Property	Mathematical Relation	Application Note
Average Number of Particles	(N{ab}(r) = \rho \int0^r !!dr' 4\pi r'^2 g_{ab}(r')) [7]	Calculates coordination numbers, e.g., the number of water molecules in the first solvation shell of an ion.
Internal Energy (Dense Fluid)	( U \approx \frac{N}{2} \rho \int_{0}^{\infty} 4\pi r^2 g(r) u(r) \, dr ) [2] (where (u(r)) is the pair potential)	The potential energy contribution from non-bonded interactions (Lennard-Jones and electrostatic) can be computed from (g(r)) and the force field's potential functions [16].
Pressure (Virial Equation)	( P = \rho kB T - \frac{\rho^2}{6} \int{0}^{\infty} 4\pi r^2 g(r) \, r \frac{du(r)}{dr} \, dr ) [2]	Relates system pressure to the derivative of the pair potential and the RDF. This is particularly sensitive to the repulsive part of the potential.
Structure Factor	( S(k) = 1 + \rho \int d\vec{r} \, e^{-i\vec{k}\cdot\vec{r}} [g(r)-1] ) [2]	Connects the RDF to scattering experiments (X-ray, neutron), allowing for direct validation of simulation results.

Experimental Protocols

Protocol: Calculating RDFs from a Molecular Dynamics Trajectory

This protocol outlines the steps for calculating a site-specific radial distribution function using MDAnalysis, a common tool for analyzing MD simulation trajectories [7].

Objective: To determine the radial distribution function (g_{ab}(r)) between two groups of atoms (or molecules) from an MD simulation trajectory.

Software and Prerequisites:

• Software: MDAnalysis library (Python) installed [7].
• Inputs:
  • A molecular dynamics trajectory file (e.g., in XTC, TRR, DCD format).
  • A topology file (e.g., in GRO, PDB format) describing the system.
  • An atom selection query for groups A and B.

Procedure:

• Load the Trajectory and Topology:

• Select Atom Groups: Define the groups of atoms between which the RDF will be calculated. For example, to study solvation of a protein backbone, Group A could be protein backbone atoms, and Group B could be water oxygen atoms.

• Initialize the RDF Analysis Module: Set up the InterRDF analyzer, specifying the two groups, the number of bins for the histogram (nbins), and the distance range (range) to analyze.

• Run the Analysis: Execute the analysis over the desired frames of the trajectory. Use the start, stop, and step parameters to control the analysis range for better statistical sampling or to manage computational cost.

• Access and Plot Results: The results are stored in rdf_analyzer.bins (the bin centers) and rdf_analyzer.rdf (the (g(r)) values).

Interpretation of RDF Output:

• Peak Position: The location of the first major peak indicates the most probable distance to the first solvation shell.
• Peak Area/Height: The magnitude of the peak relates to the probability of finding a particle at that distance. The area under the first peak, when used in the cumulative distribution function (N_{ab}(r)), gives the coordination number [7].
• Number of Peaks: The presence of secondary peaks indicates longer-range order, typically observable in more structured liquids or near solid surfaces.

Workflow: From MD Simulation to Thermodynamic Properties

The following diagram illustrates the logical workflow for connecting an MD simulation to thermodynamic insights via RDF analysis, a process foundational to the protocols described.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 3: Key Software and Analysis Tools for RDF-Based Research

Item Name	Function / Application Note
GROMACS	A robust and widely used MD simulation suite that supports most major force fields. It is used for running the production MD simulations that generate the trajectories for RDF analysis [18].
MDAnalysis	A Python library specifically designed for the analysis of MD trajectories. It contains built-in modules (MDAnalysis.analysis.rdf) for efficient calculation of both average and site-specific RDFs [7].
CHARMM/AMBER Force Fields	Classical molecular mechanics force fields that provide the empirical parameters (bonded and non-bonded interactions) for the potential energy function ((U_N)) used in the MD simulation [15] [16].
COMPASS Force Field	A force field used in MD simulations that enables accurate prediction of thermophysical properties, as demonstrated in studies of refrigerants like R-454B [17].
VMD / PyMOL	Molecular visualization software used for visual inspection of the initial protein structure, rendered trajectories, and validation of atom selections used in RDF analysis [18] [15].
PC-SAFT Equation of State	An advanced equation of state that can be parameterized using data from MD simulations (e.g., saturated density) to predict derivative thermodynamic properties like speed of sound and Joule-Thomson coefficients [17].
5-(2-Chloroethyl)-2'-deoxyuridine	5-(2-Chloroethyl)-2'-deoxyuridine (CEDU)
Sterculic acid	Sterculic Acid|Potent SCD1 Inhibitor|CAS 738-87-4

The Radial Distribution Function (RDF), typically denoted as g(r), is a fundamental statistical measure in molecular dynamics (MD) research that quantifies how particle density varies as a function of distance from a reference particle [19]. This function provides critical insights into the spatial arrangement and internal structure of materials, serving as a bridge between microscopic particle interactions and macroscopic thermodynamic properties. In molecular simulations, the RDF reveals the probability of finding a particle at a specific distance relative to the probability expected for a completely random distribution, such as in an ideal gas [19]. This makes it an indispensable tool for researchers and drug development professionals who need to characterize atomic-scale structural features that influence material behavior and binding interactions.

The power of RDF analysis lies in its ability to distinguish different states of matter through their characteristic signatures. By analyzing these signatures, scientists can infer important structural information such as coordination numbers, bonding distances, and degree of disorder within a system. Furthermore, the RDF serves as a crucial link to thermodynamic properties, enabling the calculation of system energy, pressure, and other parameters essential for understanding material behavior under different conditions [20]. For drug development applications, this structural understanding can inform decisions about molecular interactions, solvation effects, and binding affinities that are critical to pharmaceutical efficacy.

Theoretical Background: RDF Signatures Across Phases

Characteristic RDF Profiles

Each primary phase of matter exhibits a distinctive RDF signature that reflects its underlying structural organization, providing researchers with a diagnostic tool for material characterization:

• Solid Phase: The RDF of crystalline solids displays sharp, well-defined peaks at specific distances that correspond to distinct coordination shells [19]. These peaks persist to large radial distances, indicating long-range order where the positions of atoms remain correlated over considerable distances. The number, position, and relative heights of these peaks reveal information about the crystal lattice type, coordination numbers, and bond lengths characteristic of the material's ordered structure.

• Liquid Phase: Liquids exhibit a more complex RDF characterized by short-range order with diminishing correlations at larger distances [21]. The function typically shows several oscillating peaks that gradually decay to a constant value of 1, reflecting the transient local ordering of particles. The liquid state has been recently reinterpreted as a dynamic mixture of gas-like and solid-like states with alternating domination between these mechanisms [21]. This dual nature manifests in the RDF through features that suggest some residual local structure (solid-like) while lacking long-range periodicity (gas-like).

• Gas Phase: In ideal or dilute gases, the RDF is essentially flat at a value of 1 for all distances beyond the immediate exclusion zone, indicating no structural correlation between particles [19]. For real gases at higher densities, a small peak may appear at the collision diameter due to intermolecular interactions, but the rapid decay to unity confirms the absence of sustained structural organization.

Table 1: Characteristic RDF Features Across Different Phases of Matter

Phase	Short-Range Order	Long-Range Order	Peak Characteristics	Structural Interpretation
Solid	Yes	Yes	Sharp, well-defined peaks that persist	Regular, repeating lattice structure
Liquid	Yes	No	Damped oscillations that decay to unity	Local clustering without long-range correlation [21]
Gas	No	No	Flat at g(r)=1 (or minimal initial peak)	No structural correlation between particles

Theoretical Interpretation of RDF Profiles

The theoretical foundation for understanding RDF profiles stems from statistical mechanics, where g(r) connects microscopic particle interactions to macroscopic observables. In solids, the persistent oscillatory behavior in g(r) reflects the mathematical periodicity of the lattice structure, with peak positions corresponding to rational interatomic distances dictated by the crystal symmetry. The progressive damping of peak intensities with increasing distance arises from thermal vibrations and defects that slightly disrupt perfect periodicity.

In liquids, the theoretical interpretation is more complex due to the dynamic nature of the phase. The prominent first peak in the RDF corresponds to the first solvation shell, representing the most probable distance between neighboring particles. Subsequent peaks indicate second and third coordination shells, with the rapid decay of these peaks demonstrating how particle correlations diminish over distance. Recent research suggests this behavior reflects the compromise in competition between potential energy and kinetic energy in the system, where molecules transiently occupy both localized (solid-like) and delocalized (gas-like) states [21].

For gases, the theoretical expectation of a flat RDF profile derives from the assumption of minimal intermolecular interactions except during brief collision events. The theoretical connection between the RDF and thermodynamic properties enables researchers to extract quantitative information about system energy, pressure, and equation of state parameters through integral equations that relate pair distribution functions to intermolecular potentials.

Computational Protocols for RDF Analysis

Molecular Dynamics Simulation Setup

The accurate calculation of radial distribution functions requires careful implementation of molecular dynamics simulations with appropriate parameters and conditions:

• System Preparation: Begin with an initial configuration of particles in a simulation box with periodic boundary conditions applied in all three dimensions to minimize surface effects. For solids, this may be a perfect crystal lattice; for liquids, a randomized configuration; and for gases, a sparse random distribution.

• Force Field Selection: Choose appropriate interatomic potentials based on the system under investigation. For argon or other simple fluids, the Lennard-Jones potential is commonly employed with parameters (σ = 3.405 Ã…, ε = 119.8 K) that accurately reproduce physical behavior [21]. For molecular systems, more complex force fields incorporating bond stretching, angle bending, and torsion terms may be necessary.

• Equilibration Protocol: Conduct an extensive equilibration procedure to ensure the system reaches thermodynamic equilibrium before data collection. This typically involves:

  • Energy minimization to remove bad contacts
  • Gradual heating to the target temperature over 50-100 ps
  • Extended equilibration (100-500 ps) in the NVT ensemble using a Nosé-Hoover thermostat
  • Further equilibration (100-500 ps) in the NPT ensemble using a Parrinello-Rahman barostat to achieve correct density

• Production Run: Perform extended sampling in the NVE or NVT ensemble for 1-10 ns with a time step of 1-2 fs, saving trajectory frames every 1-10 ps for subsequent analysis. Longer simulations may be required for systems with slow dynamics or rare events.

RDF Calculation Methodology

The radial distribution function is calculated from MD trajectories using a histogram-based approach that accumulates pair distances over multiple simulation frames:

• Distance Binning: Define a histogram with bins of width Δr (typically 0.01-0.05 Ã…) covering the range from 0 to Rmax (usually half the box length to obey the minimum image convention).

• Pair Distance Sampling: For each reference particle i, compute distances rij to all other particles j ≠ i within the cutoff radius, excluding pairs where j is a periodic image of i.

• Histogram Accumulation: For each configuration analyzed, accumulate the count of particle pairs found within each spherical shell between r and r+Δr:

  Table 2: RDF Calculation Parameters for Different Phases

  Parameter	Solid Phase	Liquid Phase	Gas Phase
  Bin Width (Δr)	0.01-0.02 Å	0.02-0.05 Å	0.05-0.1 Å
  Maximum Radius (Rmax)	L/2	L/2	L/2
  Number of Configurations	100-1000	500-5000	1000-10000
  Sampling Frequency	Every 10-100 fs	Every 50-500 fs	Every 100-1000 fs

• Normalization: Normalize the accumulated histogram by the expected count for an ideal gas with the same density:

  g(r) = [n(r) / V(r)] / ρ

  where n(r) is the histogram count between r and r+Δr, V(r) = 4πr²Δr is the volume of the spherical shell, and ρ = N/V is the number density of the system.

• Averaging: Average the g(r) over multiple time frames and over all particles in the system to improve statistics, particularly important for disordered systems like liquids and gases where thermal fluctuations significantly impact local structure.

The following workflow diagram illustrates the complete RDF analysis protocol from simulation setup to final interpretation:

Application Notes: Structural Analysis Through RDF

Quantitative Structural Metrics from RDF

The radial distribution function provides several quantitative metrics that enable detailed structural analysis of different phases:

• Coordination Numbers: The area under the first peak of g(r) yields the average number of nearest neighbors:

  CN = 4πρ ∫₀^(r_min) r²g(r)dr

  where r_min is the position of the first minimum after the initial peak. This coordination number distinguishes local packing efficiency across phases, with solids typically showing higher, integer values (e.g., 12 for FCC), liquids having intermediate values (e.g., 10-11 for simple liquids), and gases showing minimal coordination.

• Peak Positions and Intensities: The location of the first peak (r_max) indicates the most probable interparticle distance, reflecting the balance between attractive and repulsive intermolecular forces. Peak height correlates with structural stability, with sharper, more intense peaks indicating more well-defined coordination shells.

• Structural Parameters for Different Phases of Argon:

  Table 3: Structural Parameters for Argon at 85 K (Solid), 110 K (Liquid), and 150 K (Gas) at 1 bar

  Parameter	Solid (FCC)	Liquid	Gas
  First Peak Position (Ã…)	3.76	3.72	~5.2 (weak)
  First Peak Height	3.8-4.5	2.5-3.2	~1.1
  Coordination Number	12	10.5-11.2	<1
  Long-Range Order	Yes	No	No

Advanced RDF Applications in Material Characterization

Beyond basic structural assessment, RDF analysis supports several advanced material characterization applications:

• Phase Transitions: Monitoring changes in g(r) during temperature or pressure variations provides direct evidence of phase transitions [19]. The melting of a solid manifests as a disappearance of long-range peaks in g(r), while vaporization leads to complete loss of oscillatory structure. Recent research has utilized the temperature dependence of RDF profiles to quantify the gas-like fraction in liquids, revealing the dynamic equilibrium between different molecular states [21].

• Liquid State Analysis: The complex nature of liquids makes RDF analysis particularly valuable for this phase. By applying the two-phase model (2PT) that divides liquid into solid-like and gas-like components, researchers can calculate thermodynamic properties including entropy and free energy [21]. The gas-like fraction can be determined through careful analysis of the RDF profile and its evolution with temperature.

• Material Properties Prediction: The RDF serves as input for calculating various thermodynamic properties through statistical mechanical relationships. The system energy can be obtained through:

  U = (3/2)NkT + 2πNρ ∫₀^∞ g(r)u(r)r²dr

  where u(r) is the pair potential. Similarly, pressure can be calculated using the virial equation incorporating g(r). These relationships enable researchers to connect structural information to macroscopic material behavior.

Research Reagent Solutions and Computational Tools

Successful implementation of RDF analysis requires appropriate computational tools and theoretical frameworks:

Table 4: Essential Research Reagents and Computational Tools for RDF Analysis

Tool/Resource	Type	Function	Application Context
LAMMPS	MD Software	High-performance molecular dynamics simulator	Primary simulation engine for trajectory generation
GROMACS	MD Software	Molecular dynamics package with optimized algorithms	Alternative simulation platform, especially for biomolecules
VMD	Analysis Tool	Visualization and analysis of molecular trajectories	RDF calculation, structure visualization, and trajectory analysis
MDAnalysis	Python Library	Toolkit for trajectory analysis and data processing	Custom RDF analysis workflows and batch processing
Lennard-Jones Potential	Force Field	Simple pair potential for spherical particles	Modeling noble gases (e.g., argon) and simple fluids [21]
Two-Phase Model (2PT)	Theoretical Framework	Separates liquid into solid-like and gas-like components	Calculating entropy and free energy of liquids [21]
Hypernetted Chain Closure	Integral Equation Theory	Approximate closure relation for Ornstein-Zernike equation	Calculating RDF from pair potentials without simulation

Radial distribution function analysis represents a powerful methodology for characterizing atomic-scale structure across different phases of matter within molecular dynamics research. The distinctive RDF signatures of solids, liquids, and gases provide fundamental insights into their structural organization, from the long-range order in crystals to the dynamic mixture of states in liquids [21]. The protocols outlined in this application note provide researchers with a comprehensive framework for implementing RDF analysis, from careful simulation setup through to advanced structural interpretation.

For drug development professionals, these techniques offer valuable approaches for understanding molecular interactions, solvation environments, and binding phenomena at atomic resolution. The continuing development of more sophisticated analysis methods, including improved definitions of gas-like fractions in liquids and more accurate integral equation theories, promises to further enhance the utility of RDF analysis in materials science and pharmaceutical research.

The Crucial Role of RDF in Characterizing Molecular Interactions and Hydrogen Bonding

The Radial Distribution Function (RDF), often denoted as g(r), serves as a fundamental statistical measure in molecular dynamics (MD) simulations for quantifying the probability of finding particle pairs separated by a distance r. This function provides a powerful bridge between microscopic atomic arrangements and macroscopic observable properties, offering unique insights into the structure of liquids, amorphous materials, and biological systems. For researchers investigating molecular interactions, the RDF is particularly indispensable for identifying and characterizing hydrogen bonding networks that govern the stability, dynamics, and function of biomolecular systems and complex liquid mixtures [22] [23].

In the broader context of analyzing atomic structure from MD research, RDF analysis transforms complex, time-evolving atomic coordinates into statistically robust, quantitative structural descriptors. This enables direct comparison with experimental techniques like X-ray and neutron diffraction, making MD simulations a validated "computational microscope" with exceptional resolution for observing atomic-scale phenomena that are often difficult or impossible to access experimentally [23].

Theoretical Foundation of RDF

Mathematical Formalism and Physical Interpretation

The RDF is formally defined through the relationship between the local number density of particles at a distance r from a reference particle and the global average number density of the system. For a three-dimensional system, the RDF, g(r), is calculated as:

g(r) = (1/(4πr²ρN)) · Σ Σ δ(r - rᵢⱼ)

where ρ represents the global particle number density, N is the total number of particles, and rᵢⱼ is the distance between particles i and j. The double summation is performed over all particle pairs and multiple time frames from the MD trajectory to ensure statistical significance.

The characteristic profile of an RDF plot provides immediate insights into the physical state and structural order of the system. Crystalline solids exhibit sharp, periodic peaks extending to large distances, reflecting their long-range ordered lattice arrangements. Liquids and amorphous materials display broadened peaks that decay to unity within a few molecular diameters, indicating only short-range order. In the gas phase, where atomic interactions are minimal, the RDF remains close to 1 across all distances, confirming the absence of significant structural correlation [23].

Quantitative Structural Parameters from RDF

The RDF enables extraction of precise quantitative parameters that characterize atomic-scale environments. The following table summarizes key structural information obtainable from RDF analysis:

Table 1: Quantitative Structural Parameters Derived from RDF Analysis

Parameter	Description	Extraction Method	Structural Significance
Peak Positions	Distances corresponding to high coordination probability	Local maxima in g(r) plot	Characteristic interatomic distances (e.g., first coordination shell)
Coordination Number	Average number of particles within a specific distance	Integral of 4πr²ρg(r) between limits r₁ and r₂	Quantifies local packing density and solvation
Peak Intensity	Relative probability at specific distances	Height of g(r) peaks	Strength and specificity of interactions at distance r
Peak Width	Distribution of interatomic distances	Full width at half maximum (FWHM) of peaks	Structural flexibility and thermal disorder

Integration of the RDF up to the first minimum provides the coordination number, representing the average number of neighboring particles within the first coordination shell. This parameter is particularly valuable for quantifying solvation environments and local packing densities in disordered systems [23].

RDF in Hydrogen Bonding Analysis

Characterizing Hydrogen Bond Networks

Hydrogen bonds (H-bonds) play a vital role in the stability and functioning of biomolecules, influencing protein folding, molecular recognition, and material properties. RDF analysis provides a powerful methodology for investigating the structure and dynamics of these intricate hydrogen-bonded networks. By calculating site-specific RDFs between donor (D) and acceptor (A) atoms—such as O-H∙∙∙O, N-H∙∙∙O, or O-H∙∙∙N pairs—researchers can identify characteristic H-bonding distances and quantify their relative prevalence under different conditions [22].

In complex multi-component systems, RDFs enable comparative analysis of competing molecular interactions. A study on alcohol-aniline mixtures demonstrated this capability effectively, where RDF analysis revealed the predominance of OH∙∙∙O interactions over other possible hydrogen bonds. The research further showed a "bunching of alcohol-alcohol hydrogen bonds for lower aniline concentrations, while the aniline-aniline interactions are not affected by changes in the concentration," highlighting how RDF can decipher subtle reorganization within hydrogen-bonded networks in response to changing composition [22].

Integrating RDF with Complementary Analysis Techniques

For comprehensive characterization of hydrogen bonding, RDF is typically integrated with other analytical methods:

• Hydrogen Bond Statistics: Counting specific donor-acceptor pairs within geometrically defined criteria (typically distance and angle cutoffs) to determine H-bond populations and lifetimes [22].
• Graph Theoretical Analysis (GTA): Representing hydrogen-bonded systems as mathematical graphs where atoms are nodes and H-bonds are edges, enabling analysis of network connectivity, cyclic structures, and stability using tools like the Python package NetworkX [22].

This multi-technique approach, centered around RDF analysis, provides both quantitative and topological insights into hydrogen-bonded assemblies, linking molecular-level interactions to macroscopic system properties.

Experimental Protocols and Workflows

Molecular Dynamics Simulation Setup

The following workflow outlines the key steps for performing MD simulations to generate trajectories for RDF analysis, with specific protocols for system preparation:

Figure 1: Comprehensive workflow for MD simulations from initial structure preparation to trajectory analysis for RDF calculation.

A. Initial System Preparation

• Obtain Protein Coordinates: Download the initial structure from the Protein Data Bank (http://www.rcsb.org/). Visually inspect the structure using molecular visualization tools like RasMol [18].
• Structure Preprocessing: Use a text editor to remove external water molecules and non-standard ligands. For missing atoms or residues, employ modeling tools such as Modeller or PepBuild [18].
• Force Field Selection and Topology Generation: Convert the PDB file to a GROMACS format (.gro) and generate a topology file (.top) using the pdb2gmx command:
  During this step, select an appropriate force field (e.g., ffG53A7 in GROMACS 5.1 for proteins with explicit solvent) [18].

B. Simulation System Setup

• Define Simulation Box: Create a periodic boundary condition box around the protein using the editconf command. A cubic box with a minimum 1.4 nm distance from the protein periphery is commonly used:
  The -c flag centers the protein in the box [18].
• Solvation: Add water molecules to solvate the simulation box using the solvate command:
  This updates the topology file to include water molecules [18].
• System Neutralization: Add counter ions to neutralize the system charge using the genion command. First, generate a pre-processed input file with grompp, then run genion:
  This adds sodium (NA) and chloride (CL) ions as needed to achieve overall charge neutrality [18].

C. Energy Minimization and Equilibration

• Energy Minimization: Perform energy minimization to remove steric clashes and unfavorable contacts using the mdrun command:

• System Equilibration: Equilibrate the system in two phases—first with position restraints on heavy atoms under NVT conditions (constant Number of particles, Volume, and Temperature), followed by NPT equilibration (constant Number of particles, Pressure, and Temperature) to achieve proper density.

D. Production Simulation and Analysis

• Production MD Run: Execute a production simulation without restraints to generate the trajectory for analysis. The simulation should be sufficiently long to ensure proper sampling of the phenomena of interest.
• Trajectory Analysis: Extract structural and dynamic properties, including RDF calculations, from the saved trajectory frames [18].

RDF Calculation Protocol

The specific protocol for calculating RDF from MD trajectories using GROMACS involves:

• Trajectory Preparation: Ensure the trajectory file is properly formatted and, if necessary, corrected for periodic boundary conditions using the trjconv command.
• RDF Calculation: Use the rdf analysis module in GROMACS to compute the radial distribution function between selected atom groups:
  This example calculates the RDF of water oxygen atoms around protein atoms.
• Site-Specific RDF for H-Bonds: To analyze hydrogen bonding, calculate site-specific RDFs between donor and acceptor atoms. For example, to study hydrogen bonding between alcohol and aniline molecules, compute RDFs between hydroxyl hydrogen (H) of alcohol and nitrogen (N) of aniline, and between hydroxyl oxygen (O) of alcohol and amine hydrogen (H) of aniline [22].

Essential Software and Analysis Packages

Successful implementation of MD simulations and RDF analysis requires a suite of specialized software tools. The following table details key research reagent solutions in the computational domain:

Table 2: Essential Computational Tools for MD Simulations and RDF Analysis

Tool Name	Type/Category	Primary Function	Application in RDF Analysis
GROMACS [18]	MD Simulation Suite	High-performance MD simulation engine	Generates atomic trajectories for RDF calculation; contains built-in rdf analysis tool
VMD [22]	Molecular Visualization	Trajectory visualization and analysis	Visualizing hydrogen bond networks; preliminary analysis
Python	Programming Language	Custom analysis scripting	Implementing specialized RDF calculations; data processing
NetworkX [22]	Python Library	Graph theory analysis	Analyzing topology of hydrogen-bonded networks
MDAnalysis [24]	Python Library	Trajectory analysis	Flexible RDF calculations and integration with other analyses
MDTraj [24]	Python Library	Trajectory analysis	Fast RDF calculations supporting multiple MD formats

Hardware Considerations

The computational demands of MD simulations vary significantly based on system size and simulation duration:

• Initial Setup and Preprocessing: A desktop workstation with multicore processors (e.g., Intel Core i5/i7), 16+ GB RAM, and standard graphics cards is sufficient for system setup, minimization, and equilibration [18].
• Production MD and Analysis: For production runs of biologically relevant systems, high-performance computing (HPC) resources with many cores (100+), large memory (128+ GB), and fast interconnects are typically required to achieve microsecond timescales in reasonable wall-clock time [18].

Advanced Applications and Integration

The application of RDF extends beyond simple structural characterization to advanced analysis of dynamic processes and material properties. Principal Component Analysis (PCA) can be applied to MD trajectories to extract essential collective motions from the high-dimensional coordinate data. When combined with RDF analysis, this approach helps link large-scale conformational changes to specific alterations in local atomic environments and hydrogen-bonding patterns [23].

Furthermore, RDF serves as a critical validation metric for comparing simulation results with experimental data. The direct relationship between RDF and experimentally accessible structure factors from X-ray or neutron diffraction makes it an essential tool for assessing force field accuracy and simulation reliability [23]. This validation is particularly crucial when studying hydrogen-bonded networks in binary mixtures or biomolecular systems, where accurate representation of interaction energies is essential for predictive simulations [22].

The integration of graph theoretical analysis with RDF represents a particularly powerful approach for characterizing hydrogen-bonded networks. By representing atoms as nodes and hydrogen bonds as edges, researchers can apply mathematical graph theory to quantify network connectivity, identify cyclic structures, and calculate stability metrics, providing a comprehensive topological perspective that complements the spatial statistics derived from RDF analysis [22].

Practical Implementation: Calculating RDF from MD Simulations and Biomedical Applications

Step-by-Step RDF Calculation Using MDAnalysis and LAMMPS

The Radial Distribution Function (RDF), denoted as (g(r)), is a fundamental statistical mechanics concept that characterizes the spatial arrangement of particles in a system. It describes the probability of finding a particle at a specific distance from a reference particle, providing crucial insights into the structure of liquids, ordered crystals, and disordered materials [1]. In molecular dynamics (MD) research, particularly in drug development, RDF analysis serves as an essential bridge between microscopic molecular interactions and macroscopic thermodynamic properties, enabling researchers to understand solvation shells, hydrogen bonding patterns, and ligand-protein interactions at atomic resolution [1].

The RDF effectively counts the average number of b neighbours in a shell at distance r around an a particle and represents it as a density [5]. Mathematically, for particles of type a and b, the RDF (g_{ab}(r)) is defined as:

[ g{ab}(r) = \frac{1}{N{a}} \frac{1}{N{b}/V} \sum{i=1}^{Na} \sum{j=1}^{Nb} \langle \delta(|\mathbf{r}i - \mathbf{r}_j| - r) \rangle ]

which normalizes to 1 for large separations in a homogeneous system [5] [9]. The RDF's value lies in its ability to quantify structural features that directly influence thermodynamic properties including internal energy, pressure, chemical potential, and entropy [1].

Theoretical Foundation of RDF Analysis

Key Mathematical Formulations and Structural Interpretations

The radial distribution function provides a quantitative measure of local structure against the background of a global average. When (g(r) = 1), the local density at distance (r) equals the bulk density, indicating no special structural organization. Peaks in the RDF indicate distances where neighboring atoms are more likely to be found (coordinated shells), while troughs indicate excluded dis[tances [1].

The coordination number, representing the average number of particles within a specific radius, can be derived from the RDF through the radial cumulative distribution function and the relation (N{ab}(r) = \rho G{ab}(r)), where (\rho) is the appropriate density and (G{ab}(r)) is the cumulative integral of (g{ab}(r)) [5]. This is particularly valuable for identifying solvation shell occupancies in drug-binding studies.

Table 1: Characteristic RDF Features Across Material Phases

Phase	RDF Profile Characteristics	Structural Interpretation
Crystalline Solids	Sharp, distinct peaks extending to large distances	Long-range ordered atomic arrangement
Liquids	Damped oscillatory profile with 2-3 visible peaks	Short-range order with no long-range correlation
Gases	Single peak at short distance, quickly approaching 1	Minimal structural correlation beyond direct collisions

RDF Connections to Thermodynamic Properties and Drug Development

For pharmaceutical researchers, the RDF provides critical insights into intermolecular interactions that govern drug efficacy and binding affinity. The hydrogen bond interactions essential for protein folding and protein-ligand recognition manifest as distinct peaks in the 1.5–2.5 Å range in RDF plots between donor and acceptor atoms [1]. Analysis of these specific RDF signatures enables quantitative characterization of binding site interactions and solvation effects, directly informing rational drug design approaches.

Computational Approaches for RDF Calculation

Multiple computational packages can calculate RDFs from molecular dynamics trajectories, each with distinct strengths and applications. The choice of software often depends on the simulation engine used, system size, and specific analysis requirements.

Table 2: Computational Tools for RDF Analysis from MD Simulations

Software Tool	Primary Use Case	Key Features	Trajectory Format Support
MDAnalysis	Analysis of massive trajectories [25]	Rich analysis tools, Python API, periodic boundary condition handling	LAMMPS dump, AMS, GROMACS, CHARMM, AMBER
LAMMPS compute rdf	On-the-fly analysis during simulation [26]	Built-in computation, minimal storage requirements, coordination number output	Native LAMMPS trajectories
AMS Trajectory Analysis	AMS or GCMC simulation analysis [27]	Integration with AMS package, convergence checking	AMS .rkf format
MDTraj	Small trajectories, quick analyses [25]	NumPy integration, straightforward API	Multiple formats including LAMMPS

The Scientist's Toolkit: Essential Computational Reagents

Table 3: Essential Research Reagent Solutions for RDF Calculations

Reagent Solution	Function	Implementation Examples
Distance Calculation Engine	Computes pairwise distances between atoms with PBC consideration	MDAnalysis distances module, LAMMPS neighbor lists
Histogramming Algorithm	Bins distances into radial shells for probability distribution	NumPy histogram, LAMMPS binning with Nbin parameter
Normalization Routine	Converts raw counts to probability density relative to bulk	Volume normalization by spherical shell volume
Exclusion Handling	Prevents counting of correlated atoms (bonded pairs)	exclusion_block in MDAnalysis, special_bonds in LAMMPS
Trajectory Reader	Parses MD trajectory frames for sequential analysis	MDAnalysis Universe, LAMMPS dump commands
Disulfamide	Disulfamide, CAS:671-88-5, MF:C7H9ClN2O4S2, MW:284.7 g/mol	Chemical Reagent
Epitheaflagallin 3-O-gallate	Epitheaflagallin 3-O-gallate, MF:C27H20O13, MW:552.4 g/mol	Chemical Reagent

Protocol 1: RDF Calculation with MDAnalysis

Experimental Setup and Workflow

Diagram Title: MDAnalysis RDF Calculation Workflow

Step-by-Step Implementation

• Load Trajectory and Structure Files

• Select AtomGroups for Analysis

• Configure and Run InterRDF Analysis

• Access and Visualize Results

Advanced Configuration Parameters

Table 4: MDAnalysis InterRDF Configuration Parameters

Parameter	Type	Default	Description	Recommended Value
nbins	Integer	75	Number of histogram bins	100-200 for high resolution
range	Tuple	(0.0, 15.0)	Distance range in Ångströms	System size-dependent
norm	String	'rdf'	Normalization mode: 'rdf', 'density', or 'none'	'rdf' for standard analysis
exclusion_block	Tuple	None	Prevents counting atoms from same residue/molecule	(1,1) for molecular exclusion
exclude_same	String	None	Excludes same residue/segment/chain	'residue' for intramolecular exclusion

Protocol 2: RDF Calculation with LAMMPS

Experimental Setup and Workflow

Diagram Title: LAMMPS RDF Calculation Workflow

Step-by-Step Implementation

• Basic RDF Calculation for All Atom Types

  This computes the RDF with 100 bins and outputs every 10 steps averaging over 1000 steps.

• Specific Atom Type Pair RDF Analysis

• Advanced Configuration with Cutoff Control

Output Interpretation and Key Considerations

LAMMPS compute rdf generates a global array with the bin coordinates followed by RDF and coordination number values for each specified atom type pair [26]. The output columns follow this structure:

Table 5: LAMMPS RDF Output Format Description

Column Index	Content	Units	Description
1	Bin center	Distance units	Center of radial bin
2	g(r) for pair 1	Unitless	RDF for first atom type pair
3	coord(r) for pair 1	Number	Coordination number for first pair
4	g(r) for pair 2	Unitless	RDF for second atom type pair
5	coord(r) for pair 2	Number	Coordination number for second pair

Critical Implementation Notes:

• For bonded systems, adjust special_bonds settings or use rerun command to include excluded pairs [26]
• When using cutoff keyword > force cutoff, ensure proper ghost atom communication with comm_modify cutoff [26]
• Use wildcard asterisks for type ranges (e.g., 1*3 for types 1-3) for efficient analysis of multiple type pairs

Data Analysis and Interpretation Protocol

Quantitative Analysis of RDF Features

• Identifying Solvation Shells

  • Locate the first maximum in g(r) → position of first solvation shell
  • Locate the first minimum after the peak → boundary of first solvation shell
  • Calculate coordination number at first minimum → occupancy of solvation shell

• Coordination Number Calculation

Validation and Error Analysis

• Convergence Testing

Table 6: Troubleshooting Common RDF Calculation Issues

Problem	Possible Causes	Solutions
Unphysical spikes in g(r)	Counting bonded atoms	Implement exclusion_block or adjust special_bonds
g(r) not reaching 1 at large r	Insufficient sampling	Increase trajectory frames or simulation time
Inconsistent coordination numbers	Incorrect density normalization	Verify system volume and particle counts
High noise in RDF profile	Inadequate ensemble averaging	Increase sample frames or use longer simulation

Application in Drug Development Research

Case Study: Protein-Ligand Binding Analysis

RDF analysis provides critical insights into drug binding mechanisms through:

• Hydration Shell Analysis: Calculate RDF between ligand atoms and water oxygen to identify tightly bound water molecules that mediate protein-ligand interactions.

• Direct Interaction Quantification: Compute RDF between ligand functional groups and protein binding site residues to identify and quantify specific interactions (hydrogen bonds, hydrophobic contacts).

• Solvent Accessibility: Use RDF to characterize changes in solvent structure upon ligand binding, informing entropy contributions to binding free energy.

Protocol for Binding Site Water Analysis

This protocol has detailed comprehensive methodologies for calculating and analyzing radial distribution functions using both MDAnalysis and LAMMPS. Key recommendations for robust RDF analysis in pharmaceutical research include:

• Convergence Validation: Always perform block averaging to ensure sufficient sampling, particularly for structured systems like protein-ligand complexes.

• Appropriate Exclusion Settings: Carefully exclude bonded atom pairs to avoid unphysical correlations while maintaining relevant intermolecular interactions.

• Coordination Number Integration: Use the cumulative distribution function to translate RDF profiles into quantitative coordination numbers for direct comparison with experimental data.

• Multi-Software Validation: For critical results, consider implementing parallel analysis with both MDAnalysis and LAMMPS to verify methodological consistency.

The RDF remains an indispensable tool in molecular dynamics research, providing fundamental insights into atomic-scale structure that directly connects to macroscopic properties and biological function in drug development applications.

Selection Strategies for Reference and Target Atom Groups

In molecular dynamics (MD) research, the radial distribution function (RDF) is a fundamental tool for quantifying the structure of materials and biomolecular systems. It describes how atoms are spatially distributed around a reference atom as a function of radial distance r, providing insights into local ordering, solvation shells, and material phase states [23] [3]. The validity of RDF analysis depends critically on the appropriate selection of reference and target atom groups, as improper selection can lead to physically meaningless results or the obscuring of relevant structural features. This protocol provides comprehensive guidance for defining these atom groups across diverse research scenarios, enabling researchers to extract maximum insight from their MD simulations.

Table 1: Core Definitions for RDF-Based Analysis

Term	Definition	Role in RDF Calculation
Reference Atom Group	The initial set of atoms from whose perspective the local structure is probed.	Defines the center points around which spherical shells are constructed for counting neighboring atoms.
Target Atom Group	The set of atoms whose density distribution around the reference atoms is being measured.	Provides the "neighbor" atoms counted within the spherical shells centered on each reference atom.
RDF (gₐb(r))	The probability of finding a target atom at distance r from a reference atom, normalized by the bulk density [5].	`gₐb(r) = (1/Nₐ) × (1/(Nբ/V)) × ΣΣ⟨δ(	rᵢ - rⱼ	- r)⟩` where Nₐ and Nբ are the numbers of reference and target atoms, respectively [5].

Atom Selection Syntax Across Common MD Packages

Different MD analysis packages implement similar but syntactically distinct atom selection languages. Understanding these differences is crucial for implementing portable and reproducible analysis protocols.

Table 2: Atom Selection Syntax Comparison Across MD Analysis Packages

Selection Type	CHARMM	MDAnalysis	MDTraj
Protein Atoms	SELE PROT END	"protein"	"protein"
Backbone Atoms	SELE BACKBONE END	"backbone"	"backbone"
Residue Name	SELE RESNAME LYS END	"resname LYS"	"resname LYS"
Atom Name	SELE NAME CA END	"name CA"	"name CA"
Range Query	SELE RESID 10 20 END	"resid 10:20" or "resid 10-20"	"resid 10 to 20"
Boolean Logic	SELE PROT .AND. ( .NOT. RESNAME ALA ) END	"protein and not resname ALA"	"protein and not resname ALA"
Geometric	Not standard	"around 3.5 protein"	"water and within 0.5 of resname LYS" (different implementation)

Strategic Selection for Common Research Scenarios

The appropriate strategy for selecting reference and target groups depends fundamentally on the research question. The following scenarios illustrate proven approaches for different scientific contexts.

Table 3: Selection Strategies for Common Research Scenarios

Research Scenario	Reference Group	Target Group	Key Insights
Ion Solvation Shell	Specific ion type (e.g., "resname NA" or "type NA")	Solvent atoms (e.g., "water" or "name OW" for water oxygen)	Hydration number, ion-oxygen distance, shell stability [23]
Protein Hydration	Protein surface atoms (e.g., "protein and not name H*")	Water oxygen atoms (e.g., "water and name O")	Solvent-accessible surface area, binding site water occupancy
Membrane-Protein Interface	Protein transmembrane residues (requires specific resid selection)	Lipid headgroup atoms (e.g., "resname POPC and name P" for phosphate)	Lipid binding sites, annular vs. non-annular lipid interactions
Alloy Local Ordering	One metal element (e.g., "type Al")	Another metal element (e.g., "type Ni")	Short-range ordering, compound formation tendencies, clustering
Polymer Sidechain Interactions	Specific sidechain atoms (e.g., "resname PHE and name CZ")	Another polymer segment (e.g., "backbone and name O")	Intra- vs. inter-molecular contacts, driving forces for folding

Atom Selection Workflow for RDF Analysis

Detailed Experimental Protocol for RDF Analysis

System Preparation and Preprocessing

Before calculating RDFs, proper trajectory preprocessing is essential to remove global motions that would otherwise obscure the local structure information contained in RDFs.

• Trajectory Alignment: Fit each frame of the trajectory to a reference structure to remove rotational and translational degrees of freedom. This is particularly critical for biomolecular systems where global tumbling would otherwise dominate the apparent atomic displacements [28].

• Periodic Boundary Condition Handling: Ensure continuous coordinates across periodic images. Most modern RDF implementations automatically account for periodic boundaries, but verification is recommended [28].
• Trajectory Formatting for Analysis: Reshape coordinate data as needed for analysis packages. For example, scikit-learn's PCA expects 2D input while MD trajectories typically store 3D coordinates [28]:

RDF Calculation with Exclusion Settings

Implementation specifics vary by software package, but the core algorithm remains consistent: counting target atoms in spherical shells around reference atoms.

• MDAnalysis Implementation:

  The exclusion_block parameter can exclude specific pairs from the analysis, which is particularly important for excluding bonded neighbors or atoms within the same residue [5].

• Interpreting RDF Output:

  • Peak Positions: Correspond to preferred interatomic distances (e.g., first solvation shell).
  • Peak Areas: Proportional to coordination numbers (number of neighbors in each shell).
  • Long-Range Behavior: Convergence to 1.0 indicates bulk-like behavior at large distances [23].

Table 4: Essential Computational Tools for RDF Analysis

Tool Category	Specific Examples	Primary Function	Selection Syntax Type
MD Simulation Engines	CHARMM [29], AMBER [30], GROMACS [30], NAMD [30]	Generate MD trajectories	Engine-specific (often similar to CHARMM)
Trajectory Analysis Libraries	MDAnalysis [5] [31], MDTraj [32] [28]	Post-process trajectories and calculate RDFs	Python-based, similar to CHARMM
Visualization Software	VMD [28], OVITO [3]	Visualize structures, trajectories, and analysis results	Graphical interface with text selection
Specialized Analysis Tools	LAMMPS [3], scikit-learn [28]	Advanced analysis (RDF, PCA, clustering)	Package-specific

Advanced Considerations and Troubleshooting

Statistical Quality and Sampling

RDFs require adequate sampling for convergence. Implement the following quality controls:

• Convergence Testing: Calculate RDFs over successive trajectory segments and verify consistency.
• Error Estimation: Use block averaging or bootstrap resampling to quantify uncertainty.
• Frame Selection Frequency: For long trajectories, analyze every N-th frame to balance statistical independence and computational cost.

Avoiding Common Artifacts

• Self-Interaction Artifacts: When reference and target groups overlap, exclude atoms from the same residue or molecule using exclude_same parameters [5]:

• Finite-Size Effects: For small systems, RDFs may not fully converge to 1.0 due to limited statistics and correlation effects.
• Bin Size Selection: Too few bins oversmooth features; too many introduce noise. A general guideline is 0.1 Ã… bin width, adjusted based on system size and simulation length.

RDF Profile Interpretation Guide

Appropriate selection of reference and target atom groups is not merely a technical prerequisite but a scientifically interpretive decision that directly shapes the biological or materials insights gained from RDF analysis. By applying the systematic selection strategies outlined in this protocol—tailored to specific research contexts and implemented through validated computational workflows—researchers can ensure their RDF analyses yield physically meaningful, statistically robust, and scientifically valuable structural information. As MD simulations continue to grow in scale and complexity [14] [23] [30], these fundamental selection principles will remain essential for extracting atomic-level understanding from increasingly complex simulation data.

Handling Periodic Boundary Conditions and Minimum Image Convention

In molecular dynamics (MD) simulations, researchers aim to model the behavior of macroscopic systems, but computational resources limit these studies to a relatively small number of atoms. Periodic boundary conditions (PBC) provide a solution to this challenge by enabling the simulation of a small unit cell that represents an infinite bulk system, effectively eliminating problematic surface effects that would otherwise dominate a finite cluster of atoms [33] [34]. This approach is particularly crucial when calculating properties like the radial distribution function (RDF), which describes how atomic density varies as a function of distance from a reference particle and requires a proper representation of bulk environment to yield physically meaningful results.

The implementation of PBC is intrinsically linked to the minimum image convention (MIC), a computational algorithm that ensures each particle interacts only with the single closest image of every other particle in the system [35] [36]. Within the context of a thesis employing RDF for atomic structure analysis, a proper understanding and implementation of these concepts is fundamental to obtaining accurate structural data that reliably represents true material or biomolecular properties, rather than artifacts of the simulation boundaries.

Core Concepts and Definitions

Periodic Boundary Conditions (PBC)

Periodic boundary conditions are a mathematical approach for approximating a massive, effectively infinite system by replicating a small unit cell in all spatial directions [34]. In this framework, the simulation box becomes the central unit in an infinite lattice of identical images. As particles move within the central box, their periodic images in all surrounding boxes move synchronously [37]. When a particle exits the central box through one boundary, it simultaneously re-enters through the opposite face, thereby conserving the number of particles in the primary simulation cell [33] [38].

The topology created by three-dimensional PBC is equivalent to a three-torus, where all three pairs of opposite faces are connected [34]. This periodicity creates a space without edges, which is essential for simulating bulk materials, liquids, and solvated biomolecules without introducing unphysical surface effects that would dominate a small, isolated system [33].

Minimum Image Convention (MIC)

The minimum image convention is a particle bookkeeping method that dictates that each particle in the central cell interacts only with the closest image of every other particle in the system [34] [35]. This convention prevents unphysical situations where a particle might interact with multiple images of the same particle or with itself [37].

For the MIC to be satisfied, the cutoff radius ((R_c)) used for calculating short-range non-bonded interactions must be less than half the shortest box vector [39]:

[ R_c < \frac{1}{2} \min(\|\mathbf{a}\|, \|\mathbf{b}\|, \|\mathbf{c}\|) ]

This restriction ensures that a particle cannot "see" more than one image of any other particle in the system [39]. In simulations of solvated macromolecules, an additional practical consideration requires that the box size must be large enough that the solute molecule does not interact with its own image, which would artificially affect conformational dynamics [33] [34].

Computational Implementation

Implementing PBC and MIC in Molecular Dynamics

The practical implementation of periodic boundary conditions involves specific algorithms for handling particle coordinates and calculating distances. For a cubic box with side length (L) and origin at the center, the minimum image distance calculation can be implemented as follows [34]:

This operation must be repeated in all three dimensions for cubic or rectangular boxes. For generalized triclinic cells, the implementation becomes more complex and requires transformation to fractional coordinates [39] [40].

Many MD packages, including GROMACS, AMBER, and NAMD, implement these concepts with specific commands and parameters [39] [41]. In GROMACS, for instance, the minimum image convention is combined with the concept of a "neighbor list" to efficiently compute non-bonded interactions [39] [35].

Box Geometries and Their Properties

While cubic boxes are conceptually simplest, other space-filling geometries can provide computational advantages. For simulating approximately spherical molecules like globular proteins, non-cubic boxes can significantly reduce the number of solvent molecules required, thereby improving computational efficiency [39].

Table 1: Comparison of Common Periodic Box Types in Molecular Dynamics

Box Type	Image Distance	Relative Volume	Number of Images	Typical Applications
Cubic	(d)	(d^3) (1.00)	26	Simple liquids, crystals
Rhombic Dodecahedron (xy-square)	(d)	(\frac{1}{2}\sqrt{2}d^3) (0.71)	12	Solvated globular proteins
Rhombic Dodecahedron (xy-hexagon)	(d)	(\frac{1}{2}\sqrt{2}d^3) (0.71)	12	Membrane proteins
Truncated Octahedron	(d)	(\frac{4}{9}\sqrt{3}d^3) (0.77)	18	Solvated biomolecules

The rhombic dodecahedron is particularly noteworthy as it represents the smallest and most regular space-filling unit cell, with each of its 12 image cells at the same distance [39]. This shape saves approximately 29% of the CPU time compared to a cubic box with the same image distance when simulating spherical or flexible molecules in solvent [39].

Handling Long-Range Interactions

The implementation of a cutoff radius for non-bonded interactions creates special challenges for different types of potentials. Van der Waals interactions, described by the Lennard-Jones potential, decay rapidly with distance ((r^{-6})) and can be safely truncated with modest correction terms [37]. In contrast, electrostatic interactions decay much more slowly ((r^{-1})) and require special treatment to avoid significant errors [37].

The most common approach for handling long-range electrostatic interactions under PBC is the Ewald summation method, particularly the Particle Mesh Ewald (PME) algorithm, which efficiently calculates electrostatic forces by splitting them into short-range real-space and long-range reciprocal-space components [39] [41]. Most modern MD packages, including AMBER, GROMACS, and NAMD, implement PME for accurate electrostatic calculations [41].

Workflow and Protocols

System Setup and PBC Implementation

The following workflow outlines the key steps for properly implementing periodic boundary conditions in a molecular dynamics simulation, particularly in the context of preparing systems for RDF analysis.

Figure 1: Workflow for implementing periodic boundary conditions in molecular dynamics simulations.

The protocol for implementing PBC begins with system preparation, where the molecular coordinates are centered in an appropriately sized simulation box [41]. The choice of box geometry should balance computational efficiency against potential artifacts; for RDF analysis of isotropic systems, rhombic dodecahedra often provide optimal efficiency [39].

Box dimensions must be selected to ensure the minimum image convention is satisfied. A common recommendation for biomolecular simulations is to maintain at least 1.0-1.5 nm of solvent between any protein atom and its periodic image [33] [34]. This ensures that the solute molecule does not artificially interact with its own images, which could corrupt RDF calculations.

For electroneutrality, the system must have zero net charge when using Ewald methods for electrostatics, as a charged unit cell would create an infinite Coulomb potential when replicated [34]. This is typically achieved by adding appropriate counterions (e.g., Na⁺ or Cl⁻) to neutralize the system [34] [41].

Practical Protocol for RDF-Focused Simulations

• System Setup:

  • Center the molecule(s) of interest in a sufficiently large box
  • For RDF analysis of solvation structure, ensure minimum solute-image distance exceeds twice the intended RDF cutoff
  • Select box geometry appropriate for the system (cubic for solids, rhombic dodecahedron for solutions)

• Solvation and Neutralization:

  • Add explicit solvent molecules using tools like Solvate in Chimera or similar utilities in GROMACS/NAMD [41]
  • Add ions to neutralize system charge and achieve physiological ionic strength if appropriate

• Parameter Configuration:

  • Set non-bonded cutoff to less than half the shortest box dimension: (R_c < \frac{1}{2} \min(\|{\bf a}\|,\|{\bf b}\|,\|{\bf c}\|)) [39]
  • Configure Particle Mesh Ewald for electrostatic interactions [41]
  • Set neighbor list update frequency appropriate for particle diffusion

• Simulation Stages:

  • Energy minimization to relieve atomic clashes while maintaining PBC
  • Equilibration with position restraints on solute atoms, gradually relaxing constraints
  • Production simulation with full PBC for RDF data collection

• RDF Analysis:

  • Calculate RDF using trajectory analysis tools
  • Ensure proper handling of periodic images in distance calculations
  • Verify RDF decays to unity at large distances, confirming adequate system size

Table 2: Key Parameters for PBC Implementation in RDF Calculations

Parameter	Typical Setting	Rationale	Impact on RDF
Box Type	Rhombic Dodecahedron	Minimizes solvent molecules while maintaining isotropy	Improves sampling efficiency
Cutoff Radius	≤ 0.9 × half shortest box vector	Ensures MIC compliance	Prevents artifacts at RDF cutoff
Solvent Padding	≥ 1.0 nm	Prevents solute-solute image interactions	Ensures proper bulk solvent region
PME Grid Spacing	0.1-0.16 nm	Accurate long-range electrostatics	Correct ion distribution in RDF
Neighbor List Update	10-20 steps	Maintains MIC while optimizing speed	Ensures all relevant pairs counted

The Scientist's Toolkit

Successful implementation of periodic boundary conditions and minimum image convention requires both specialized software and understanding of key computational concepts. The following tools and concepts form the essential toolkit for researchers employing PBC in molecular dynamics simulations.

Table 3: Essential Research Reagents and Computational Tools

Tool/Category	Specific Examples	Function in PBC/MIC Implementation
MD Simulation Packages	GROMACS, AMBER, NAMD [39] [41] [42]	Provide built-in PBC handling, neighbor lists, and Ewald methods
System Preparation Tools	Solvate [41], editconf [39], PACKMOL	Create solvated systems in appropriate box geometries
Analysis Software	MDAnalysis [42], MDtraj [42], VMD	Calculate RDFs with proper periodic corrections
Force Fields	AMBER [41], CHARMM, OPLS-AA	Provide parameters for bonded and non-bonded interactions under PBC
Long-Range Electrostatics	Particle Mesh Ewald [41], PPPM [39]	Handle slowly-decaying Coulomb interactions in periodic systems
Box Types	Cubic, Rhombic Dodecahedron, Truncated Octahedron [39]	Provide space-filling unit cells with different efficiency characteristics
iso-OMPA	iso-OMPA, CAS:513-00-8, MF:C12H32N4O3P2, MW:342.36 g/mol	Chemical Reagent
Diazaquinomycin A	Diazaquinomycin A	Diazaquinomycin A is a potent natural product for anti-tuberculosis research. This product is For Research Use Only (RUO). Not for human or veterinary use.

Troubleshooting and Artifacts

Despite proper implementation, PBC can introduce artifacts that affect structural analysis. A common issue in RDF calculations is the truncation effect when the cutoff distance approaches half the box size, causing the RDF to artificially drop before the cutoff [37]. This can be mitigated by using sufficiently large boxes or correction methods.

For charged systems, improper neutralization can cause severe artifacts in ion distribution functions, as the Ewald summation method requires net neutral unit cells [34]. Always verify system neutrality before production simulations.

In membrane systems or other anisotropic environments, two-dimensional PBC (slab boundary conditions) may be more appropriate, with PBC applied only in the planar dimensions and a vacuum or non-periodic boundary in the perpendicular direction [34].

The flying ice cube effect, where kinetic energy partitions unevenly between different molecular components, can be addressed by using appropriate thermostats and removing center-of-mass motion [41] [42].

When analyzing trajectories for RDF calculations, researchers must ensure that their analysis tools properly handle periodic boundaries, as improper implementation can introduce errors in pair distribution functions, particularly at larger distances where periodic imaging becomes relevant.

Analyzing Solvation Shells and Coordination Numbers in Biomolecular Systems

The solvation shell, the immediate layer of solvent molecules surrounding a solute, is a critical determinant of structure, dynamics, and function in biomolecular systems. In aqueous environments, the specific organization of water molecules around proteins, nucleic acids, and small molecules directly influences folding, binding, and catalytic activity. For metal ions, which are essential cofactors in numerous biological processes, the solvation shell's structure dictates reactivity, transport, and selectivity. A precise understanding of these hydration environments is therefore paramount in drug development, where modulating solvation effects can lead to optimized ligand binding and specificity.

The radial distribution function (RDF), denoted as g(r), is a fundamental statistical mechanics tool for quantifying solvation shell structure from molecular dynamics (MD) trajectories. It describes the probability of finding a particle at a distance r from a reference particle, relative to a uniform distribution. Key structural parameters extracted from RDFs include coordination numbers (CN), which specify the average number of solvent molecules within the first solvation shell, and ion-oxygen/ion-nitrogen distances, which define the geometry of the solvation complex.

This Application Note provides a practical guide for employing RDF analysis to characterize solvation environments in biomolecular systems, with detailed protocols and contemporary examples from the literature.

Theoretical Background: The Radial Distribution Function (RDF)

The RDF, or pair correlation function, is defined for a spherically symmetric system as:

[Formula for g(r)]

From the RDF, the coordination number CN can be calculated by integrating the number of particles (ρ) within a spherical shell up to the first minimum (rmin) of the RDF:

[Formula for CN]

In biomolecular simulations, this allows for the precise quantification of how many water molecules, on average, are directly coordinated to a metal ion or reside in the first hydration layer of a specific protein atom or ligand.

Computational Protocols

Molecular Dynamics Simulation Setup

Objective: To generate a stable MD trajectory for subsequent RDF analysis of a solvated biomolecular system.

Materials:

• Software: GROMACS, AMBER, NAMD, or LAMMPS.
• Force Field: Compatible with the system (e.g., OPLS-AA, CHARMM, AMBER). Specialized parameters may be needed for metal ions [43].
• System: Solute (protein, DNA, metal complex) solvated in a water box (e.g., SPC/E, TIP3P, TIP4P). Ions should be added to neutralize the system.

Procedure:

• System Building: Place the solute in the center of a simulation box. Solvate the system with an appropriate water model. Add ions to achieve electro-neutrality and, if desired, physiological concentration.
• Energy Minimization: Use the steepest descent or conjugate gradient algorithm to remove steric clashes and bad contacts.
• Equilibration: a. NVT Ensemble: Equilibrate the system for 100-500 ps at the target temperature (e.g., 300 K) using a thermostat (e.g., Nosé-Hoover, Berendsen). b. NPT Ensemble: Further equilibrate the system for 100-500 ps at the target pressure (e.g., 1 bar) using a barostat (e.g., Parrinello-Rahman, Berendsen).
• Production Run: Perform an unrestrained MD simulation for a duration sufficient to achieve good statistical sampling (typically tens to hundreds of nanoseconds). Save the trajectory at regular intervals (e.g., every 10 ps).

RDF and Coordination Number Analysis

Objective: To calculate the RDF and coordination number for a specific atom pair from the production MD trajectory.

Procedure:

• Trajectory Processing: Ensure the trajectory is properly centered and that periodic boundary conditions are handled correctly. Remove rotational and translational motions if necessary.
• RDF Calculation: Use the analysis tools within your MD software (e.g., gmx rdf in GROMACS). Specify the reference group (e.g., a metal ion or protein atom) and the target group (e.g., water oxygen or nitrogen atoms).
• Identify Key Features: From the plotted RDF, identify the position of the first peak (r_max), which corresponds to the most probable distance in the first solvation shell. The first minimum (r_min) after this peak defines the upper distance limit of the first shell.
• Calculate Coordination Number: Integrate the RDF up to r_min to obtain the running coordination number. The value at r_min is the average coordination number for the first solvation shell.

Table 1: Key Physical Probes for Solvation Shell Analysis

Probe	Target	Extracted Parameter	Biological Relevance
Water Oxygen	Metal Ion (e.g., Mg2+)	Ion-O distance, CN	Ion mobility, ligand exchange rates [43] [44]
Water Oxygen	Protein Atom/Solute	Solute-O distance, CN	Hydrophobicity, binding site accessibility
Water Hydrogen	Anion (e.g., Cl−)	Anion-H distance, CN	Anion stability and shielding [44]
Cosolute/Solvent	Metal Ion / Solute	Preferential binding, CN	Solvent specificity, ion selectivity [45]

The following workflow summarizes the end-to-end process from simulation setup to analysis and interpretation:

Application Examples in Biomolecular Systems

Probing Water Structure in Redox Biochemistry

The redox state of biomolecules can be probed by analyzing their effect on surrounding water. A 2025 study on glutathione successfully differentiated its reduced (GSH) and oxidized (GSSG) states by combining near-infrared spectroscopy with MD-derived RDFs [46]. The RDF for water molecules around the sulfur atom showed a first peak at approximately 3.8 Ã… that was twice as high for GSH compared to GSSG, indicating a greater number of water molecules interacting with the thiol (-SH) sulfur. This difference in the hydration structure, quantified by RDF, provided a physical basis for the spectral differences observed, enabling non-invasive redox state monitoring [46].

Table 2: Experimentally Validated Coordination Numbers from MD Simulations [44]

Ion	Coordination Number (CN) from CPMD	Reported Experimental Range	Remarks
Na+	5.0 – 5.5	4.8 – 5.3 (Neutron Diffraction) [44]	Consistent with dissociative/Id ligand exchange [43].
K+	6.0 – 6.5	4.8 – 6.0 (Neutron Diffraction) [44]	Larger, more diffuse shell than Na+.
Cl−	5.3 – 6.4	6.2 – 6.4 (<2 M conc.) [44]	Coordination number is concentration-dependent.

Modeling Ligand Exchange in Metalloenzymes

Metal ions like Mg²⁺ are ubiquitous in biology, and their function often involves the exchange of water ligands for substrate atoms. Modeling this process is challenging for classical force fields. A 2025 study demonstrated that Machine Learning Potentials (MLPs) can accurately model the structure and ligand exchange dynamics of Mg²⁺ in water [43]. The MLP-trained model reproduced the known octahedral [Mg(H₂O)₆]²⁺ complex with a Mg–O distance of 2.10 Ã… and successfully simulated the microsecond-timescale water exchange, which proceeds via a dissociative or interchange-dissociative mechanism [43]. This approach is directly applicable to studying metal ion catalysis in enzyme active sites.

Investigating Ion Selectivity and Hydration

The distinct hydration structures of Na⁺ and K⁺, as detailed in Table 2, are a classic example of how RDF analysis informs biology. The lower coordination number of Na⁺ (∼5.5) compared to K⁺ (∼6.5) and the shorter ion-oxygen distance result from its higher charge density. This difference is exploited by ion channels, whose selectivity filters are finely tuned to mimic the native hydration shell of the preferred ion, enabling exquisite selectivity (e.g., 1000:1 for K⁺ over Na⁺ in potassium channels) [44]. Ab initio MD simulations confirm these coordination numbers, which are consistent with X-ray and neutron scattering data [44].

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Computational and Experimental Reagents for Solvation Studies

Reagent / Tool	Function / Description	Example Use Case
Machine Learning Potentials (MLPs)	High-accuracy, computationally efficient potentials trained on QM data.	Modeling ligand exchange in Mg2+ and Pd2+ complexes [43].
Ab Initio MD (CPMD)	DFT-based MD for electronic structure accuracy.	Probing ion-water interaction energies and hydration shell geometry [44].
OPLS-AA Force Field	Classical force field for biomolecular systems.	Simulating hybrid water-in-salt electrolyte structure [45].
Near-Infrared (NIR) Spectroscopy	Non-destructive technique sensitive to water molecular conformations.	Differentiating redox states of glutathione via solvation shell analysis [46].
LiTFSI Salt	Bis(trifluoromethane)sulfonimide lithium salt; high solubility.	Creating super-concentrated "water-in-salt" electrolytes for studying unique solvation structures [45].
Anthra(1,2-b)oxirene, 1a,9b-dihydro-	Anthra(1,2-b)oxirene, 1a,9b-dihydro-	Anthra(1,2-b)oxirene, 1a,9b-dihydro- is a high-purity oxirene-fused anthracene derivative for research in organic electronics and medicinal chemistry. For Research Use Only. Not for human or veterinary use.
Fumigatin	Fumigatin, CAS:484-89-9, MF:C8H8O4, MW:168.15 g/mol	Chemical Reagent

Advanced Techniques and Future Outlook

Advanced force fields and analysis methods are pushing the boundaries of solvation science. The diagram below illustrates the hierarchy of computational methods used to model solvation shells, from fast but approximate classical force fields to highly accurate but computationally expensive ab initio methods, with MLPs offering a promising middle ground.

Emerging experimental techniques provide powerful validation. Intermolecular Radiative Decay (IRD) is a novel, non-local X-ray emission process that can selectively probe the electronic structure of the solvation shell around ions like Na⁺ and Mg²⁺ from within the bulk solution [47]. This selectivity offers a unique opportunity to directly benchmark the predictions of MD simulations regarding the ion-solvent interaction.

The analysis of solvation shells and coordination numbers via RDFs from MD simulations is an indispensable tool for elucidating the structure-function relationship in biomolecular systems. The protocols and examples outlined herein provide a framework for researchers to rigorously characterize hydration environments, from simple ionic solutions to complex protein-ligand interactions. The continued integration of advanced computational methods like MLPs with cutting-edge experimental probes like IRD promises to further deepen our understanding of solvation, driving innovations in drug design and biomolecular engineering.

The Epidermal Growth Factor Receptor (EGFR) and H-Ras proteins are critical components in cellular signaling pathways that regulate key processes including cell proliferation, survival, and differentiation. Dysregulated activation of EGFR and mutations in H-Ras are frequently implicated in human cancers, making them prominent targets for therapeutic intervention [48] [49]. Understanding protein-ligand interactions in these systems is fundamental to advancing drug discovery efforts.

This case study employs Molecular Dynamics (MD) simulations to investigate these interactions at an atomic level. A powerful statistical mechanics tool, the Radial Distribution Function (RDF), is applied to analyze simulation trajectories. The RDF, denoted as g(r), describes the probability of finding a particle at a distance r from a reference particle, providing deep insights into molecular structure, intermolecular interactions, and thermodynamic properties within the system [1]. This methodology offers a robust framework for characterizing the spatial organization of atoms around binding sites and quantifying interaction strengths, which is essential for rational drug design.

Theoretical Background

EGFR and H-Ras in Signaling and Cancer

EGFR is a single-pass transmembrane protein belonging to the ErbB receptor family. Its structure consists of an extracellular ligand-binding domain, a transmembrane domain, and an intracellular tyrosine kinase domain. Upon binding to ligands such as Epidermal Growth Factor (EGF) or Transforming Growth Factor α (TGFα), EGFR undergoes conformational changes that activate its intracellular kinase domain, initiating downstream signaling cascades like the Ras/Raf/MEK/ERK pathway [48]. The dysregulation of this pathway is observed in approximately one-third of all human cancers [49].

The Ras/Raf/MEK/ERK signaling pathway transduces signals from extracellular receptors to the cell nucleus, regulating biological functions including cell proliferation, differentiation, and apoptosis [49]. H-Ras is a key GTPase protein in this pathway, acting as a molecular switch. Oncogenic mutations in H-Ras can lock it in a constitutively active GTP-bound state, leading to continuous signaling and tumorigenesis.

Radial Distribution Function in MD Analysis

The Radial Distribution Function (RDF) is a fundamental concept in statistical mechanics that bridges microscopic particle arrangements with macroscopic observable properties [1]. In the context of MD simulations of biological systems, the RDF is crucial for:

• Characterizing Solvation Shells: Identifying the precise arrangement and density of water molecules or ions around specific protein atoms.
• Mapping Binding Sites: Quantifying the probability of finding ligand atoms near key residues in a protein's active site.
• Calculating Thermodynamic Properties: The RDF serves as the primary link for computing system energy, pressure, and entropy based on intermolecular interactions [1].

The RDF for a system is calculated by constructing a series of concentric spherical shells around a reference atom and computing the average particle density in each shell relative to a homogeneous system [1]. The mathematical formulation for the RDF g(r) between particle types a and b is: [g{ab}(r) = (N{a} N{b})^{-1} \sum{i=1}^{Na} \sum{j=1}^{Nb} \langle \delta(|\mathbf{r}i - \mathbf{r}j| - r) \rangle] where (Na) and (Nb) are the numbers of particles, (\mathbf{r}i) and (\mathbf{r}_j) are their positions, and (\delta) is the Dirac delta function [7].

Table 1: Key RDF Features and Their Interpretations in MD Studies

RDF Feature	Structural Interpretation	Significance in Protein-Ligand Systems
Peak Position	Preferred distance between particle pairs	Identifies strong specific interactions (e.g., hydrogen bonds)
Peak Height	Strength of interaction at that distance	Indicates probability/affinity of the interaction
Peak Width	Flexibility or distribution of distances	Suggests the rigidity or freedom of the atomic pair
Coordination Number	Average number of particles within a distance	Quantifies solvation or binding stoichiometry

Methodology

Workflow for RDF Analysis from MD Simulations

The following diagram outlines the comprehensive protocol from system setup to RDF analysis.

Detailed Experimental Protocols

Protocol 1: System Preparation and MD Simulation

• Initial Structure Retrieval:

  • Obtain high-resolution crystal structures of the EGFR kinase domain (e.g., PDB ID: 1M17) or H-Ras (e.g., PDB ID: 4Q21) from the Protein Data Bank [49].
  • Use structural bioinformatics tools like PRISM to analyze protein-protein interfaces if complexes are not fully available [49].

• System Construction:

  • Use molecular visualization and simulation software (e.g., VMD, CHARMM-GUI).
  • Parameterize small molecule ligands using tools like CGenFF or GAAMP.
  • Solvate the protein-ligand complex in a cubic water box with TIP3P water molecules, maintaining a minimum 10 Ã… buffer between the protein and box edge.
  • Add ions (e.g., Na⁺, Cl⁻) to neutralize the system's net charge and simulate physiological salt concentration (e.g., 150 mM NaCl).

• Energy Minimization and Equilibration:

  • Perform 5,000 steps of energy minimization using the steepest descent algorithm to remove bad atomic contacts.
  • Equilibrate the system in the NVT ensemble (constant Number of particles, Volume, and Temperature) for 100 ps, gradually heating the system to 310 K using a Langevin thermostat.
  • Further equilibrate in the NPT ensemble (constant Number of particles, Pressure, and Temperature) for 100 ps, maintaining a pressure of 1 atm using a Nosé-Hoover barostat.

• Production MD Simulation:

  • Run a production simulation for a minimum of 100 ns (longer for complex conformational changes) with a 2-fs time step.
  • Apply periodic boundary conditions and use particle mesh Ewald (PME) for long-range electrostatic interactions.
  • Save atomic coordinates every 10 ps for subsequent analysis (resulting in 10,000 frames per 100 ns simulation).

Protocol 2: RDF Calculation and Analysis

• Trajectory Processing:

  • Ensure the trajectory is properly aligned (e.g., to the protein backbone) to remove global rotation and translation.

• RDF Computation:

  • Utilize analysis tools like MDAnalysis [7] or GROMACS built-in tools.
  • Define atom groups for analysis. For example:
    • Reference group: Specific protein atoms (e.g., NZ atom of a critical lysine in EGFR's binding site).
    • Target group: Ligand atoms (e.g., oxygen atoms in a carboxylate group) or water oxygen atoms.
  • Use the InterRDF function in MDAnalysis [7] with parameters: nbins=75 and range=(0.0, 15.0) to compute the RDF, g(r), over a 15 Ã… range.

• Data Interpretation:

  • Identify peaks in the g(r) plot. The first major peak indicates the distance of the closest, most probable interaction.
  • Calculate the coordination number (average number of target atoms within a specific cutoff distance, r) by integrating the RDF [7] [1]: [N{ab}(r) = \rho \int0^r !!dr' 4\pi r'^2 g_{ab}(r')] where (\rho) is the average number density of the target atoms in the system.

The Scientist's Toolkit

Table 2: Essential Research Reagents and Computational Tools

Item / Resource	Function / Description	Application in EGFR/H-Ras Study
Protein Data Bank (PDB)	Repository for 3D structural data of proteins and nucleic acids [49].	Source for initial EGFR and H-Ras coordinates (e.g., PDB IDs 1M17, 4Q21).
PRISM Web Server	Prediction tool for protein-protein interactions at the structural level [49].	Models complexes for EGFR dimerization or H-Ras/effector interfaces when experimental structures are unavailable.
MDAnalysis Library	Python library for analyzing MD simulation trajectories [7].	Implements InterRDF class for calculating radial distribution functions from trajectory data.
CHARMM36 Force Field	A set of parameters for simulating biomolecular systems, including proteins, lipids, and nucleic acids.	Provides energy terms for bonds, angles, dihedrals, and nonbonded interactions in MD simulations.
Tipranavir & Indinavir	FDA-approved HIV protease inhibitors identified as potential repurposing candidates [49].	Serve as example ligands for studying interaction with EGFR and ERBB3/HER3 interfaces.
GROMACS	A software package for performing MD simulations, primarily used for biomolecules.	Performs the energy minimization, equilibration, and production MD runs.
Solavetivone	Solavetivone, CAS:54878-25-0, MF:C15H22O, MW:218.33 g/mol	Chemical Reagent

Results and Data Presentation

Applying the RDF analysis to MD trajectories of EGFR and H-Ras systems yields quantitative data on atomic-scale interactions. The following tables summarize key findings from such analyses, illustrating how RDFs can differentiate binding modes and interaction strengths.

Table 3: Example RDF Analysis of Water Oxygen Atoms Around Key Residues

Protein System	Reference Atom	First Peak Distance (Ã…)	First Peak g(r)	Coordination Number
EGFR (Apo)	Catalytic Lys (NZ)	2.85	2.91	6.8
EGFR + Tipranavir	Catalytic Lys (NZ)	2.82	1.45	1.2
H-Ras (GTP-bound)	Mg²⁺ Ion	2.10	5.20	6.0
H-Ras (GDP-bound)	Mg²⁺ Ion	2.11	4.95	5.9

Table 4: RDF Analysis of Potential Ligand Atom Interactions with EGFR

Ligand	Ligand Atom Group	Protein Atom/Residue	First Peak Distance (Ã…)	Interaction Type Inferred
Tipranavir	Carboxylate O	Lys745 (NZ)	2.85	Strong Ionic / H-bond
Tipranavir	Hydroxyl O	Thr790 (OG1)	2.95	H-bond
Indinavir	Hydroxyl O	Asp855 (OD1)	2.91	H-bond
Indinavir	Aromatic Ring	Phe856 (Aromatic Ring)	3.55	π-π Stacking

Discussion

The RDF data provides a quantitative measure of the structural and dynamic changes induced by ligand binding. In the example data (Table 3), the significant decrease in the first peak g(r) value and coordination number for water around the catalytic Lysine in the EGFR+Tipranavir complex indicates ligand displacement of water molecules from the binding site—a key driver of binding affinity. The sharp, high peak for the Mg²⁺ ion solvation shell in H-Ras (Table 3) confirms its stable, octahedral coordination, which is crucial for GTP binding and hydrolysis.

The application of RDF analysis extends to evaluating drug repurposing candidates. For instance, research suggests that HIV protease inhibitors like Tipranavir and Indinavir may bind to the interface of EGFR and ERBB2/HER2 [49]. MD simulations of these proposed complexes, followed by RDF analysis of key interfacial residues, can validate and characterize these interactions, providing a structural basis for repurposing.

This case study demonstrates that integrating MD simulations with RDF analysis creates a powerful framework for dissecting protein-ligand interactions in therapeutically relevant systems like EGFR and H-Ras, offering invaluable insights for drug discovery and repositioning.

The Radial Distribution Function (RDF), denoted as g(r), is a fundamental statistical mechanics concept that characterizes the spatial arrangement of particles in a system. It describes the probability of finding a particle at a specific distance from a reference particle, providing crucial insights into the structure of liquids, ordered crystals, and disordered materials [1]. In the context of molecular dynamics (MD) simulations for drug design, the RDF serves as a powerful tool that bridges microscopic molecular interactions with macroscopic observable properties. The RDF effectively counts the average number of b neighbours in a shell at distance r around an a particle and represents it as a density [7]. This capability is indispensable for identifying binding sites and understanding allosteric networks, as it allows researchers to quantify the dynamic interactions between drugs and their protein targets, as well as the propagation of allosteric signals through a protein's structure.

Table 1: Key RDF Features and Their Significance in Drug Design

RDF Feature	Structural Interpretation	Relevance to Drug Design
Peak Position	Preferred interatomic distance	Identifies strong interaction distances (e.g., hydrogen bonds)
Peak Height	Strength of interaction at distance r	Quantifies binding affinity and specificity
Peak Width	Flexibility of interaction	Indicates conformational flexibility of binding site
Coordination Number	Average number of particles within radius r	Characterizes solvation shells and ligand coordination

RDF Fundamentals and Calculation Methods

Mathematical Foundation

The RDF g_{ab}(r) between types of particles a and b is formally defined as:

g_{ab}(r) = (N_{a} N_{b})^{-1} \sum_{i=1}^{N_a} \sum_{j=1}^{N_b} \langle \delta(|\mathbf{r}_i - \mathbf{r}_j| - r) \rangle

which is normalized so that the RDF becomes 1 for large separations in a homogeneous system [7]. The RDF illustrates how particle density varies as a function of the distance r from a reference particle. At very small interatomic distances, the RDF is zero, as repulsive forces prevent molecular overlap. The first peak appears at the contact distance, representing the most probable distance for molecular interactions [1].

The radial cumulative distribution function is given by:

G_{ab}(r) = \int_0^r !!dr' 4\pi r'^2 g_{ab}(r')

and the average number of b particles within radius r is:

N_{ab}(r) = \rho G_{ab}(r)

where ρ is the appropriate density. This function can compute coordination numbers, such as the number of neighbors in the first solvation shell N(r₁), where r₁ is the position of the first minimum in g(r) [7].

Computational Implementation

In practice, calculating the RDF involves selecting an atom within the system as a reference, constructing a series of concentric spherical shells around this atom, and then counting the number of atoms residing within each shell over multiple simulation snapshots [1]. The average is divided by the volume of the corresponding shell and the system's number density to obtain g(r).

For MD trajectory analysis, specialized software packages like MDAnalysis [7] and VMD [4] provide optimized implementations. These tools can handle the computationally expensive task of histogramming distances between atom pairs while accounting for periodic boundary conditions through the minimum image convention. The computational expense scales with system size, but GPU-accelerated algorithms can dramatically improve performance, with reported speedups of 92x compared to CPU implementations [4].

Application to Binding Site Identification

Characterizing Protein-Ligand Interactions

RDF analysis provides a quantitative method for identifying and characterizing binding sites by examining the distribution of specific atom types around potential binding pockets. When a ligand binds to a protein, it establishes characteristic distances to protein residues that can be detected as distinct peaks in the RDF. For instance, hydrogen bonding interactions typically produce sharp peaks in the range of 1.5–2.5 Å for donor-acceptor distances, while hydrophobic interactions produce broader peaks at longer distances [1].

In drug design applications, comparing RDFs between different ligand candidates and a target protein reveals critical information about binding modes and interaction strengths. A higher first peak in the RDF indicates stronger, more specific interactions, while the presence of multiple well-defined peaks suggests a stable, well-ordered binding geometry. The coordination number obtained by integrating the RDF provides insight into the number of specific interactions (e.g., hydrogen bonds, halogen bonds, or π-π stacking interactions) that contribute to binding affinity.

Solvation Analysis

RDFs are particularly valuable for studying the hydration structure of binding sites, which is crucial for understanding the thermodynamics of ligand binding. The displacement of water molecules from a binding site upon ligand binding is a major driver of binding affinity. By calculating RDFs of water oxygen atoms around key binding site residues, researchers can identify tightly bound water molecules that might be important for protein function and should be conserved in drug design, as well as displaceable water molecules whose displacement could enhance binding affinity.

Table 2: Characteristic RDF Peaks for Common Molecular Interactions in Drug Design

Interaction Type	Typical RDF Peak Position (Ã…)	Peak Characteristics	Interpretation in Binding
Hydrogen Bond	1.5–2.5	Sharp, intense	Strong, directional interaction
Hydrophobic Contact	3.5–5.5	Broad, moderate	Nonspecific, entropically driven
Ionic Interaction	2.5–3.5	Sharp, variable height	Strong electrostatic attraction
π-π Stacking	3.5–4.5	Moderate, may have multiple peaks	Aromatic-aromatic interaction
Water Bridging	1.5–2.5 & 3.5–5.0	Two correlated peaks	Indirect ligand-protein interaction

Protocol: RDF Analysis for Binding Site Characterization

System Setup and Trajectory Preparation

Step 1: Molecular Dynamics Simulation

• Perform MD simulation of the protein-ligand system using packages like NAMD, GROMACS, or AMBER with appropriate force fields.
• Ensure sufficient sampling (typically hundreds of nanoseconds) with frames saved at regular intervals (e.g., every 100 ps).
• Maintain constant temperature and pressure (NPT ensemble) closer to physiological conditions.

Step 2: Trajectory Processing

• Remove translational and rotational motions by aligning each frame to a reference structure.
• Ensure trajectory format compatibility with analysis tools (e.g., DCD, XTC, TRR).

RDF Calculation Using MDAnalysis

Step 3: Atom Selection

Step 4: RDF Computation

Step 5: Coordination Number Calculation

Data Analysis and Interpretation

Step 6: Peak Identification and Quantification

• Identify peak positions corresponding to specific molecular interactions.
• Calculate coordination numbers by integrating RDF up to the first minimum.
• Compare peak heights and positions across different ligand candidates or mutant proteins.

Step 7: Visualization and Reporting

• Plot RDFs with clearly labeled peaks and coordination numbers.
• Create comparative plots for different systems or conditions.
• Correlate RDF features with binding affinity measurements.

Elucidating Allosteric Networks with RDF Analysis

Allosteric Communication in Proteins

Allostery is a ubiquitous phenomenon where binding or disturbance of a distal site in a protein can functionally control its activity, considered as the "second secret of life" [50]. Allosteric drugs are increasingly used because they produce fewer side effects, as allosteric signal propagation does not stop at the 'end' of a protein but may be dynamically transmitted across the cell [51]. The concept of allosteric drugs can be broadened to 'allo-network drugs' – whose effects can propagate either within a protein or across several proteins to enhance or inhibit specific interactions along a pathway [51].

At the molecular level, allosteric regulation occurs through population shifts in conformational ensembles. Proteins exist as ensembles of states, and the 'population' of each state (conformation) determines the protein's functional properties. Allosteric effectors work by stabilizing specific conformational states, thereby shifting the population distribution and modulating protein activity [51]. This mechanism differs fundamentally from orthosteric inhibition and offers advantages in specificity and reduced toxicity.

RDF Signatures of Allosteric Communication

RDF analysis can detect and quantify allosteric effects by monitoring changes in atomic spatial distributions upon allosteric modulator binding. When an allosteric effector binds, it induces long-range structural and dynamic changes that alter the preferred distances between atom pairs in distal functional sites. These changes manifest as:

• Alterations in peak heights of RDFs between residue pairs along allosteric pathways
• Shifts in peak positions indicating tightening or loosening of interactions
• Changes in coordination numbers reflecting altered packing densities

For example, in studies of adenosine A1 receptor (A1R) activation and G-protein coupling, researchers have combined MD simulations with network analysis to decipher activation pathways and identify transient conformational states involved in allosteric communication [52]. RDF analysis of specific residue pairs along these pathways can provide quantitative measures of these allosteric transitions.

Protocol: Mapping Allosteric Networks with RDF

Identifying Allosteric Pathways

Step 1: System Selection and Setup

• Select protein systems with known or suspected allosteric regulation.
• Perform MD simulations of both apo and holo (allosteric effector-bound) forms.
• Include control simulations with orthosteric ligands for comparison.

Step 2: Residue Pair Selection for RDF Analysis

• Identify potential allosteric pathways using computational tools like AlloMAPS [53] or SBSMMA (Structure-Based Statistical Mechanical Model of Allostery) [53].
• Select residue pairs along predicted communication pathways for RDF analysis.
• Include control residue pairs not involved in allosteric communication.

RDF Analysis of Allosteric Communication

Step 3: Site-Specific RDF Calculations

Step 4: Comparative RDF Analysis

• Calculate difference RDFs (Δg(r)) between apo and holo forms.
• Identify statistically significant changes in peak positions and heights.
• Map significant changes onto protein structure to visualize allosteric pathways.

Step 5: Network Analysis Integration

• Correlate RDF changes with allosteric network properties.
• Identify key residues with largest RDF changes as potential control points.
• Validate predictions with experimental data or mutational studies.

Table 3: Research Reagent Solutions for RDF-Based Allosteric Studies

Reagent/Software	Function	Application Context
MDAnalysis [7]	Python library for MD analysis	RDF calculation and trajectory analysis
VMD with GPU Acceleration [4]	Visualization and analysis	High-performance RDF computation
AlloSigMA [53]	Allosteric signaling analysis	Identifying allosteric sites and pathways
SBSMMA [53]	Statistical mechanical modeling	Quantifying allosteric energetics
Markov State Models	Conformational ensemble analysis	Identifying allosteric states
NMR Spectroscopy [50]	Experimental validation	Verifying computational predictions

Case Studies in Drug Design

KRasG12D Allosteric Inhibition

The K-RasG12D oncoprotein represents a challenging drug target due to the stereochemical properties of its active site, which hampered the development of orthosteric drugs [53]. Using the computational framework based on SBSMMA, researchers have designed allosteric effectors by starting from fragments of known well-characterized drugs and optimizing them to bind designated binding sites for obtaining highly specific and tunable allosteric signaling [53]. RDF analysis of MD simulations played a crucial role in characterizing the allosteric communication between the effector binding site and the switch I and II regions of K-Ras.

In this approach, RDFs between key residues in the allosteric site and functional regions showed significant changes upon effector binding, indicating strengthened or weakened interactions along the allosteric pathway. The coordination numbers derived from these RDFs provided quantitative measures of the allosteric effects, enabling fine-tuning of effector candidates via fragment-based design.

SARS-CoV-2 Main Protease (MPro) Allosteric Modulation

For the SARS-CoV-2 main protease (MPro), a high-throughput per-residue quantification of the energetics of allosteric signaling and effector binding revealed known drugs capable of inducing the required modulation upon binding [53]. RDF analysis helped identify allosteric sites distinct from the catalytic site and characterize the communication pathways between these sites and the active site.

The RDFs between residue pairs along these pathways showed distinct signatures in the presence of allosteric effectors, providing a quantitative basis for virtual screening of potential allosteric modulators. This approach expanded the targetable sites on MPro beyond the active site, offering new opportunities for drug development against COVID-19.

Advanced Applications and Future Directions

Multi-Scale Modeling Integration

The integration of RDF analysis with multi-scale modeling approaches represents a powerful strategy for advancing allosteric drug design. By combining atomistic MD simulations with coarse-grained models and network-based analyses, researchers can bridge spatial and temporal scales to comprehensively characterize allosteric mechanisms [50]. RDFs provide the crucial atomic-level detail needed to validate and refine coarse-grained models, ensuring they accurately capture essential interactions.

Machine Learning Enhancement

Machine learning approaches, particularly deep learning, are increasingly being applied to predict allosteric sites and design allosteric modulators [50]. RDF data from MD simulations can serve as valuable features for training these models, providing quantitative descriptors of atomic spatial distributions that correlate with allosteric regulation. The combination of RDF analysis with machine learning holds promise for accelerating the discovery of allosteric drugs by enabling rapid screening of potential binding sites and effector molecules.

Allo-Network Drug Discovery

The concept of "allo-network drugs" extends traditional allosteric modulation by considering the propagation of allosteric effects across cellular networks rather than just within individual proteins [51]. RDF analysis can contribute to this emerging paradigm by quantifying how allosteric effects in one protein alter its interactions with binding partners, potentially leading to network-wide effects. This approach may enable the development of drugs that achieve specific, limited changes at the systems level, potentially resulting in fewer side effects and lower toxicity.

Optimizing RDF Calculations: Parameter Selection, Performance, and Accuracy

The radial distribution function (RDF) is a fundamental statistical mechanics concept that characterizes the spatial arrangement of particles in a system, describing the probability of finding a particle at a specific distance from a reference particle [1]. In molecular dynamics (MD) research, RDF analysis serves as a crucial bridge between microscopic molecular interactions and macroscopic thermodynamic properties [13] [1]. The reliability and resolution of RDF results depend critically on the appropriate selection of computational parameters: bin size (Δr), range (rmax), and trajectory length (Nframes) [4]. This protocol provides detailed guidance for researchers on optimizing these parameters to ensure statistically robust and physically meaningful RDF calculations in drug development and materials science applications.

Parameter Selection Guidelines

Core Parameter Definitions and Quantitative Recommendations

Table 1: Optimal Parameter Ranges for RDF Analysis in MD Studies

Parameter	Definition	Impact on Analysis	Recommended Range	Special Considerations
Bin Size (Δr)	Width of histogram bins for distance distribution	Smaller Δr increases resolution but reduces signal-to-noise ratio; larger Δr smooths data but may obscure details [4]	0.1 - 0.5 Å	Balance spatial resolution with statistical sampling; use smaller bins for short-range interactions [7]
Range (rmax)	Maximum distance for RDF calculation	Determines the extent of spatial correlations captured; must comply with periodic boundary conditions [4]	≤ L/2 (half the box length) [4]	Must be less than or equal to half the simulation box width to avoid artifacts [4]
Trajectory Length (Nframes)	Number of MD frames used for averaging	More frames improve statistical accuracy but increase computational cost [4]	Minimum: 1000 frames for reasonable statistics [1]	Dependent on system size and diffusion rates; larger systems require more sampling [4]

Advanced Considerations for Specific Research Applications

Table 2: Application-Specific Parameter Optimization

Research Application	Bin Size (Δr)	Range (rmax)	Trajectory Requirements	Key RDF Features
Solvation Shell Analysis [54]	0.1 Ã… (high resolution for peak position)	5-10 Ã… (capture 1st/2nd solvation shells)	Focus on equilibrium phase; multiple independent trajectories	First peak position and integration for coordination numbers
Hydrogen-Bonding Studies [1]	0.1-0.2 Ã… (resolve short distances)	3.5 Ã… (typical H-bond range)	Ensure adequate sampling of bonding dynamics	First peak at 1.5-2.5 Ã… (O-H or N-H) [1]
Ion-Ion Correlation in Solutions	0.2-0.5 Ã…	15-20 Ã… (capture long-range ordering)	Extended simulations for slow ion dynamics	Oscillatory patterns indicating ionic structure
Protein-Ligand Interactions [55]	0.2-0.5 Ã…	5-8 Ã… (binding site region)	Multiple ligand orientations and binding events	Specific atom-atom correlations in binding pocket

Experimental Protocol for RDF Calculation

Workflow for RDF Analysis

Step-by-Step Implementation Guide

System Preparation and Trajectory Handling

• Centering and Alignment: Center the protein or molecule of interest in the simulation box and superimpose each frame onto a reference structure to maintain a consistent frame of reference [54] [55]. This is crucial for studying solvent density around proteins or specific binding sites [54].
• Periodic Boundary Artifacts: Ensure all molecules are made whole that may have been broken across periodic boundaries, and remap solvent molecules to be closest to the solute [54] [55]. For distance calculations, compute the minimum image distance using the formula:

Parameter Optimization and Calculation

• Bin Size Selection:
  • Start with a bin size of 0.1 Ã… for high-resolution analysis of first solvation shell [7]
  • If statistical noise is excessive, increase to 0.2-0.5 Ã… while monitoring the effect on peak resolution [4]
  • For coordination number calculations, ensure bin size is small enough to accurately capture the first minimum position

• Range Determination:

  • Set the maximum range rmax to half the smallest box dimension: rmax ≤ min(Lx, Ly, L_z)/2 [4]
  • For solvation studies, typically 5-10 Ã… suffices to capture the first few solvation shells [54]
  • For ionic systems or long-range correlations, extend to 15-20 Ã… if box size permits [1]

• Trajectory Sampling:

  • Use a minimum of 1000 frames for reasonable statistics [1]
  • Ensure frames span the entire equilibrium region of the simulation, excluding equilibration phases
  • For slow dynamics, use multiple independent trajectories rather than a single long trajectory
  • Check convergence by comparing RDFs from first and second halves of the trajectory

RDF Calculation and Normalization

• Pair Distance Calculation: For each frame, compute distances between all atom pairs in the selections, applying minimum image convention [4]
• Histogram Accumulation: Bin distances into histogram with chosen Δr and rmax [4]
• Normalization: Normalize the histogram by the number of reference particles, the ideal gas density, and the volume of each spherical shell [2]:

The Scientist's Toolkit

Table 3: Essential Software Tools for RDF Analysis

Tool Name	Functionality	Application Context	Key Features
VMD [4]	Trajectory visualization and analysis	GPU-accelerated RDF calculations for large systems	Multi-GPU implementation; 92x speedup over CPU [4]
MDAnalysis [7]	Python library for MD analysis	Flexible RDF implementation with various normalizations	InterRDF and InterRDF_s classes for different analysis types [7]
GROMACS [56]	MD simulation engine	Built-in RDF calculations during simulation	gmx rdf tool for efficient trajectory analysis
MDTraj [57]	Python library for trajectory analysis	Fast RDF calculation from saved trajectories	Integration with ForceBalance for parameter optimization [57]
OpenMM [57]	GPU-accelerated MD simulation	Custom RDF analysis via Python API	High-performance computing capabilities

Computational Considerations and Validation

Performance Optimization Strategies

• GPU Acceleration: Implement RDF calculations on GPUs using tiling schemes to maximize data reuse at the fastest levels of the GPU memory hierarchy [4]. Modern implementations show 92x speedup on four NVIDIA GeForce GTX 480 GPUs compared to CPU implementations [4].
• Load Balancing: For multi-GPU configurations, use dynamic load balancing to maintain high performance on heterogeneous GPU setups [4].
• Memory Management: Utilize atomic memory operations available on state-of-the-art GPUs to use on-chip memory more efficiently, resulting in fivefold performance increases compared to algorithms without atomic operations [4].

Validation and Quality Control

• Convergence Testing: Split trajectory into multiple blocks and compute RDFs for each block to ensure consistency [1].

• Coordination Number Calculation: Integrate RDF to obtain coordination numbers:

  Nab(r) = 4πρb ∫0^r gab(r')r'²dr'

  where ρ_b is the bulk density of type b particles [7].

• Experimental Validation: Compare with experimental RDFs from X-ray or neutron scattering where available [1] [57]. Tools like ForceBalance can systematically fit force field parameters by targeting experimental RDFs [57].

Application in Drug Development

In pharmaceutical research, RDF analysis provides insights into solvation structure, hydrogen bonding, and molecular interactions critical for drug solubility and binding [56]. Machine learning analysis of MD trajectories has identified key properties influencing drug solubility, including features derived from RDF analysis such as the average number of solvents in the solvation shell (AvgShell) [56]. These analyses rely on proper parameter selection to generate meaningful descriptors for predictive models in drug development pipelines [58] [56].

In the analysis of atomic structures from Molecular Dynamics (MD) research, the radial distribution function (RDF) serves as a fundamental tool for quantifying molecular structure and interactions. The RDF, denoted as (g(r)), is a measure of the probability of finding a particle at a distance (r) from a reference particle, relative to what would be expected for a random distribution at the same density [13] [2]. In statistical mechanics, it provides a statistical description of local packing and particle density in a system [13]. For intramolecular studies, a critical technical challenge involves implementing proper exclusion protocols to manage correlations between atoms that are part of the same molecule or residue, ensuring that calculated properties are not artificially skewed by bonded interactions or spatially proximate atoms that do not represent meaningful structural features. When a given particle is taken to be at the origin O, and if (\rho = N/V) is the average number density of particles, then the local density at distance (r) is given by (\rho g(r)) [2]. This document details application notes and protocols for managing these exclusions within the context of a broader thesis on using RDF for MD-based atomic structure analysis.

Theoretical Foundation: RDFs and the Need for Exclusions

The radial distribution function is formally defined for a system of (N) particles in volume (V) at temperature (T). The n-particle density correlation function, (\rho^{(n)}(\mathbf{r}1, \ldots, \mathbf{r}n)), describes the probability of finding particles 1 to n at positions (\mathbf{r}1) to (\mathbf{r}n) [2]. For the pair correlation function ((n=2)), this is related to the RDF. In a homogeneous system, the RDF (g_{ab}(r)) between particle types (a) and (b) is calculated as:

[g{ab}(r) = (N{a} N{b})^{-1} \sum{i=1}^{Na} \sum{j=1}^{Nb} \langle \delta(|\mathbf{r}i - \mathbf{r}_j| - r) \rangle]

This function is normalized to approach 1 for large separations in a homogeneous system [7]. The RDF effectively counts the average number of (b) neighbours in a shell at distance (r) around an (a) particle and represents it as a density [7].

In intramolecular RDF calculations, the failure to exclude certain atom pairs leads to erroneous results. Specifically, atoms connected by bonded interactions (bond lengths, bond angles, and dihedral angles) or atoms within the same residue exhibit spatial correlations that are not representative of the overall molecular structure or dynamics. These excluded interactions are a standard component of molecular mechanics force fields, which calculate non-bonded and bonded interactions using a particle-based description of the system [16]. Modern MD simulations employ these force fields, where molecules are represented by particles representing atoms or groups of atoms with assigned electric charges and a potential energy function [16].

Table 1: Common Intra-molecular Atom Pairs Requiring Exclusion Protocols

Atom Pair Relationship	Typical Interaction Type	Impact on RDF if Not Excluded
Directly bonded atoms (1-2 pairs)	Bond stretching	Introduces a large, artificial peak at very short distances (~1-1.5 Ã…)
Atoms separated by one bond (1-3 pairs)	Angle bending	Introduces artifactual peaks at short distances (~2-2.5 Ã…)
Atoms separated by two bonds (1-4 pairs)	Dihedral torsion	May introduce less pronounced, but still artifactual, structural peaks
Atoms within the same residue	Combination of bonded and non-bonded	Artificially inflates local density, masking true solvation structure

Computational Protocols and Implementation

General Workflow for Exclusion Management

The following diagram illustrates the logical workflow for implementing exclusion protocols in intra-molecular RDF analysis.

Diagram Title: Workflow for Intra-molecular RDF Exclusion Protocols

Protocol 1: Exclusion via theexclusion_blockParameter (MDAnalysis)

The InterRDF class in MDAnalysis provides a direct mechanism for handling exclusions via the exclusion_block keyword argument [7]. This is particularly useful for excluding pairs of atoms from within the same molecule.

Detailed Methodology:

• System Setup and AtomGroup Definition:

  • Load your MD trajectory and topology into MDAnalysis.
  • Define two AtomGroups (g1 and g2) between which the intra-molecular RDF will be calculated. These could be, for example, the same group to analyze all intra-molecular pairs or specific functional groups within the molecule.

• Exclusion List Generation:

  • Analyze the topology to identify the number of atoms per molecule (atoms_per_molecule).
  • The exclusion_block parameter accepts a tuple (m, n) representing a tile to exclude from the distance matrix. For a molecule with 7 atoms, using exclusion_block=(7, 7) would mask all pairs where the two atoms are from the same molecule [7]. This effectively excludes all intra-molecular pairs in a single step.

• RDF Calculation:

  • Initialize the InterRDF object with the AtomGroups and the exclusion_block parameter.

• Analysis:

  • The resulting RDF (rdf.rdf) and the bin centers (rdf.bins) can be plotted or analyzed further. The RDF will now reflect only the inter-molecular correlations, free from intra-molecular bonding artifacts.

Table 2: Key Research Reagent Solutions for RDF Analysis with Exclusions

Tool/Solution	Type	Primary Function in Exclusion Protocols
MDAnalysis (Python)	Software Library	Provides the InterRDF class with exclusion_block for systematic exclusion of same-molecule atom pairs [7].
GROMACS mdrun	MD Engine	Generates simulation trajectories using force fields that inherently define 1-2, 1-3, and 1-4 exclusions for non-bonded interactions.
CHARMM/AMBER Force Fields	Parameter Set	Defines the molecular topology, including the list of bonded atoms and the associated exclusion rules for non-bonded calculations [16].
InterRDF_s (MDAnalysis)	Software Class	Calculates site-specific RDFs for lists of AtomGroup pairs, allowing for custom, pair-specific exclusion logic [7].
VMD measure gofr	Analysis Script	Can compute RDFs with built-in options to skip bonded pairs based on topological information.

Protocol 2: Manual Pair Selection for Specific Residue Analysis

For higher-resolution analysis, such as studying correlations between specific atoms in the same residue while excluding others, a manual pair selection strategy is more appropriate. The InterRDF_s class in MDAnalysis is designed for this purpose [7].

Detailed Methodology:

• Site-Specific Pair Definition:

  • Instead of providing two large AtomGroups, you provide a list of pairs of AtomGroups to InterRDF_s [7]. For example, to study the distance between a sidechain nitrogen and backbone oxygens in the same residue, you would create a list where each entry is a pair of AtomGroups containing just those specific atoms for each residue of interest.

• Implicit Exclusion:

  • By explicitly defining only the atom pairs of interest, all other atoms (including those that are bonded and would normally require exclusion) are automatically omitted from the calculation. This method offers maximum control.

• RDF Calculation and Cumulative Analysis:

  • Run the calculation. The result is a list of site-specific RDFs.
  • You can also compute the radial cumulative distribution function, (G{ab}(r) = \int0^r !!dr' 4\pi r'^2 g_{ab}(r')), which gives the average number of (b) particles within radius (r) [7].

The following diagram illustrates the logical decision process for selecting the appropriate exclusion protocol based on the research question.

Diagram Title: Protocol Selection Logic for Exclusion Management

Application Note: Case Study in a Protein System

Consider an MD simulation of a protein in explicit solvent. A researcher aims to understand the spatial distribution of alpha-carbon atoms relative to each other along the polypeptide chain, excluding the trivial bonded neighbors.

Application of Protocol:

• Objective: Calculate the intra-protein RDF between Cα atoms, excluding pairs that are adjacent in sequence (1-2 pairs) and those that are one residue apart (1-3 pairs).
• Implementation: Using MDAnalysis, the researcher would create an AtomGroup ca containing all Cα atoms. The exclusion_block parameter cannot be used here as the protein is a single molecule. Instead, a custom distance calculation or the manual creation of an exclusion list based on residue index separation (e.g., excluding pairs where |i - j| < 3) would be necessary. This could be achieved by pre-calculating a distance matrix and masking the relevant indices before histogramming.
• Outcome: The resulting RDF, (g_{C\alpha-C\alpha}(r)), would reveal the average spatial distribution of Cα atoms, highlighting peaks corresponding to recurring structural motifs like alpha-helical turns or beta-sheet spacings, free from the artificial peaks of the peptide backbone's bonded structure.

This refined analysis, made possible by robust exclusion protocols, provides deeper insights into the internal packing of the protein and can be critical for comparing mutant structures, assessing folding stability, or validating simulation force fields against experimental data.

GPU Acceleration and Parallel Computing for Large-Scale RDF Analysis

Radial Distribution Function (RDF) analysis is a crucial technique in molecular dynamics (MD) research for characterizing atomic and molecular structures. It describes how particle density varies as a function of distance from a reference particle, providing insights into material properties, solvation effects, and molecular interactions relevant to drug development. As MD simulations grow to encompass billions of particles, traditional computational approaches become prohibitively slow. This application note details how GPU acceleration and parallel computing strategies enable efficient RDF analysis of large-scale systems, facilitating research that was previously computationally intractable.

Performance Advantages of GPU Acceleration

GPU-accelerated computing provides significant performance improvements for RDF analysis compared to traditional CPU-based approaches. The massively parallel architecture of modern GPUs is ideally suited to the computational patterns required for particle pair analysis in molecular dynamics.

Table 1: Performance Comparison of Computing Architectures for Molecular Dynamics

Computing Architecture	System Size	Relative Performance	Key Advantage
Multi-CPU (16-64 cores)	500,000 particles	1x (baseline)	Established implementation
Single GPU	500,000 particles	5-20x faster [59]	Massive parallelism
Multi-Node, Multi-GPU	Up to 10 billion particles [59]	Previously inaccessible scales	Distributed memory architecture

The performance advantages stem from two key design principles: (1) performing all computations exclusively on GPUs to minimize CPU-GPU data exchange, and (2) implementing efficient communication patterns among GPUs in multi-node setups [59]. This "GPU-resident" approach eliminates the data transfer bottleneck that often plagues hybrid CPU-GPU implementations.

Computational Framework and Implementation

GPU-Optimized RDF Algorithms

The InterRDF_s class in MDAnalysis provides a foundation for site-specific RDF calculations, enabling analysis between selected atomic sites and their surrounding environment [60]. When adapted for GPU execution, the algorithm undergoes several optimizations:

• Parallel pair distance computation: Calculating distances between all particle pairs is distributed across thousands of GPU threads
• Bin assignment parallelism: Histogram bin updates for RDF calculation are performed concurrently with atomic operations
• Memory coalescing: Data access patterns are structured to maximize memory bandwidth utilization

For systems with heterogeneous particle types, additional optimizations include sorting particles by type to minimize thread divergence and implementing efficient filtering masks for selective RDF analysis.

Multi-Layer Parallelization Strategy

Effective large-scale RDF implementation employs three parallelization layers:

• Inter-node parallelism: Distributes workload across multiple computing nodes using Message Passing Interface (MPI)
• Inter-GPU parallelism: Divides computational tasks among GPUs within and across nodes
• Intra-GPU parallelism: Leverages thousands of GPU cores for parallel execution of particle-pair calculations [59]

This hierarchical approach enables the analysis of systems comprising billions of particles while maintaining efficient resource utilization.

Experimental Protocol for GPU-Accelerated RDF Analysis

System Setup and Preparation

Table 2: Research Reagent Solutions for GPU-Accelerated RDF Analysis

Component	Specification	Function/Role
MD Simulation Software	MDAnalysis with GPU-enabled RDF modules [60]	Framework for trajectory analysis and RDF computation
Computing Hardware	Multi-node, multi-GPU cluster (e.g., NVIDIA A100, AMD Radeon RX 7800) [59] [61]	Provides parallel processing capability for large-scale computation
Molecular Dynamics Engine	OCCAM, GROMACS, NAMD, or HOOMD with GPU support [59]	Generates particle trajectory data through MD simulation
Analysis Environment	Python with NumPy, Matplotlib, and CUDA/OpenACC [60]	Data processing, visualization, and custom algorithm development

Step-by-Step Protocol

• Trajectory Preparation

  • Generate molecular dynamics trajectories using GPU-accelerated MD software (e.g., OCCAM, GROMACS)
  • Ensure trajectory files contain appropriate particle identifiers and coordinates
  • Validate data integrity and unit consistency across the dataset

• GPU-Accelerated RDF Computation

  • Initialize GPU device and allocate memory for particle coordinates and RDF histogram bins
  • Transfer particle data to GPU global memory in batched segments if necessary
  • Execute parallel RDF kernel with optimized thread block and grid dimensions
  • Implement multiple kernel passes for large systems that exceed GPU memory capacity

• Data Analysis and Visualization

  • Transfer RDF results from GPU to host memory for analysis
  • Normalize RDF values by system density and particle counts
  • Generate publication-quality visualizations using plotting libraries
  • Perform statistical analysis on RDF profiles to extract structural parameters

Validation and Quality Control

• Verify RDF normalization by checking convergence to unity at large distances
• Compare GPU results with established CPU implementations for consistency
• Perform unit tests on known systems with analytical solutions
• Monitor GPU memory usage to prevent allocation failures during execution

Advanced Implementation Considerations

Memory Management Strategies

Efficient GPU memory management is critical for large-scale RDF analysis. Key strategies include:

• Batched processing: Dividing large systems into manageable segments that fit within GPU memory constraints
• Memory reuse: Implementing circular buffers to minimize allocation/deallocation overhead
• Unified Memory: Utilizing CUDA Unified Memory for systems with complex memory access patterns

Optimization Techniques

• Thread coarsening: Combining multiple computations per thread to reduce scheduling overhead
• Shared memory utilization: Storing frequently accessed data in fast shared memory
• Kernel fusion: Combining multiple computational steps into single kernels to reduce global memory access

Application in Drug Development Research

For pharmaceutical researchers, GPU-accelerated RDF analysis enables detailed investigation of drug-receptor interactions, solvation effects around candidate molecules, and assembly of complex biomolecular systems. The dramatically reduced computation time facilitates high-throughput analysis of multiple drug candidates or simulation conditions, providing structural insights that complement experimental data.

The scalability of these approaches allows researchers to study increasingly realistic systems, including full protein complexes in physiological environments, at a level of detail that was previously impossible. This enhances the predictive power of molecular simulations in drug design and optimization workflows.

Addressing Statistical Uncertainties in Sparse and Complex Systems

In molecular dynamics (MD) research, the radial distribution function (RDF) is a fundamental metric that reveals the probability of finding particle pairs as a function of their separation distance, thereby providing crucial insights into the local structure and ordering within a system [62]. However, when analyzing sparse systems—such as dilute solutions, low-density materials, or systems with limited sampling—or complex systems featuring heterogeneity and rare events, statistical uncertainties in RDF analysis become a significant challenge. These uncertainties can obscure true structural features, lead to misinterpretation of intermolecular interactions, and ultimately compromise the reliability of scientific conclusions drawn from MD simulations. This application note provides a structured framework and detailed protocols for quantifying, managing, and mitigating these statistical uncertainties, ensuring robust structural analysis within the broader context of atomic-scale research.

Background and Theoretical Framework

The radial distribution function, (g{AB}(r)), between particles of type A and B is formally defined as [62]: [ g{AB}(r) = \frac{1}{\langle\rhoB\rangle{local}} \frac{1}{NA} \sum{i \in A}^{NA} \sum{j \in B}^{NB} \frac{\delta(r{ij} - r)}{4\pi r^2} ] where (\langle\rhoB(r)\rangle) represents the particle density of type B at distance (r) around particles A, and (\langle\rhoB\rangle{local}) is the average particle density of type B over all spheres around particles A with radius (r{max}).

In sparse systems, such as dilute colloidal solutions or low-density regions of biomolecules, the limited number of particle pairs within relevant distance ranges leads to poor sampling and high-variance RDF estimates. In complex systems, including nanoparticles with gradient architectures or multicomponent biomolecular assemblies, structural heterogeneity introduces additional challenges for obtaining statistically representative RDFs [63]. Proper uncertainty quantification is not merely a statistical formality but an essential component of rigorous structural analysis, as results without uncertainty estimates risk being "unusable collections of senseless numbers" [64].

Table 1: Primary Sources of Statistical Uncertainty in RDF Analysis

Uncertainty Source	Impact on RDF	Typical Magnitude	Dependence Factors
Finite Sampling	High-frequency noise, reduced peak definition	5-15% for sparse systems [65]	Simulation length, system size, particle density
Sparse Data	Increased variance at mid-long range	10-25% for (r > \text{1nm}) [66]	Number of particle pairs, concentration
Structural Heterogeneity	Inconsistent profiles across regions	5-20% variance [63]	System composition, spatial organization
Boundary Effects	Artificial truncation at box edges	1-5% error [62]	Simulation box size, cut-off selection
Discretization Error	Bin-dependent peak shifting	1-3% error [62]	Bin width, interpolation method

Protocol for Robust RDF Analysis in Sparse Systems

Enhanced Sampling Methodology

Objective: Obtain statistically reliable RDF profiles from systems with limited particle counts. Materials:

• MD simulation trajectory of the sparse system
• Trajectory analysis software (GROMACS gmx rdf [62], MDTraj [57])
• Statistical analysis environment (Python/R for bootstrap analysis)

Procedure:

• Trajectory Preparation:
  • Ensure trajectory frames are properly aligned and periodic boundary conditions are correctly handled
  • Verify system sparsity: if particle counts < 1000, implement enhanced sampling protocols [66]

• Multi-frame RDF Calculation:

  • Use -bin 0.01 for fine resolution (0.01 nm bins)
  • Set -n index.ndx to define specific atom groups for pairwise analysis
  • Process minimum of 1000 frames for sparse systems [65]

• Block Averaging Implementation:

  • Divide trajectory into 5-10 blocks of equal duration
  • Calculate RDF for each block independently
  • Compute mean RDF and standard error across blocks

• Statistical Convergence Test:

  • Monitor RDF variance as function of trajectory length
  • Continue sampling until key peak heights vary by <5% with additional frames [65]

Uncertainty Quantification Protocol

Objective: Quantify statistical uncertainties in computed RDF profiles. Procedure:

• Bootstrap Resampling:
  • Generate 100-500 synthetic datasets by resampling frames with replacement
  • Compute RDF for each resampled dataset
  • Calculate 95% confidence intervals from bootstrap distribution [66]

• Differential Entropy Assessment:
  • Apply model-free information entropy metric [66]: [ \delta \mathcal{H}(\mathbf{Y}|{\mathbf{X}i}) = -\log\left[\sum{i=1}^n Kh(\mathbf{Y}, \mathbf{X}i)\right] ]
  • High entropy values indicate rare or poorly sampled atomic environments
  • Identify regions where (\delta \mathcal{H} > 2.0) as uncertainty hotspots [66]

Protocol for Complex and Heterogeneous Systems

Subpopulation RDF Analysis

Objective: Resolve structural heterogeneity in complex systems like nanoparticles or multicomponent assemblies. Materials:

• MD trajectory of heterogeneous system
• Spatial clustering algorithm (K-means, DBSCAN)
• Machine learning environment (Scikit-learn for K-neighbors classification [63])

Procedure:

• Spatial Domain Identification:
  • Perform clustering based on local atomic environments [63]
  • Use symmetry functions or atom-centered descriptors to characterize environments [66]
  • Identify distinct structural regions (core, shell, interface)

• Domain-Specific RDF Calculation:

  • Compute RDFs separately for each identified domain
  • Compare intra-domain vs inter-domain RDFs
  • Use ML classification to verify architectural sensitivity [63]

• Architectural Sensitivity Analysis:

  • Apply K-Neighbors classification to theoretical RDFs
  • Validate method achieves >99% confidence in architecture determination [63]
  • Transfer approach to experimental RDFs from EXAFS data [63]

Information-Theoretic Assessment

Objective: Quantify dataset completeness and identify rare events. Procedure:

• Atom-Centered Descriptor Calculation:
  • For each atom, compute sorted distance vector to k-nearest neighbors [66]: [ \mathbf{X}i^{(1)} = \left[\frac{w(r{i1})}{r{i1}}, \ldots, \frac{w(r{ik})}{r{ik}}\right]^T ]
  • Augment with angular information through neighbor-pair distances [66]: [ X{in}^{(2)} = \left\langle \frac{\sqrt{w(r{ij})w(r{il})}}{r{jl}}\right\ranglen ]

• Information Entropy Computation:
  • Employ kernel density estimation with Gaussian kernel [66]: [ \mathcal{H}({\mathbf{X}}) = -\frac{1}{n}\sum{i=1}^n \log\left[\frac{1}{n}\sum{j=1}^n Kh(\mathbf{X}i, \mathbf{X}_j)\right] ]
  • Interpret results: ( \mathcal{H} \approx 0 ) indicates homogeneous sampling; ( \mathcal{H} \approx \log n ) suggests diverse, potentially undersampled environments [66]

Experimental Validation and Force Field Optimization

RDF-Targeted Force Field Parameterization

Objective: Optimize force field parameters to reproduce experimental RDFs with uncertainty propagation. Materials:

• ForceBalance optimization toolkit [57]
• Reference experimental RDF data
• Quantum chemistry calculation capability (DFT)

Procedure:

• Objective Function Definition:
  • Compute mean squared difference (MSD) between computed and experimental RDFs [57]: [ A = \frac{1}{N} \sum{n=1}^N \left[\text{RDF}{\text{comp}}(n) - \text{RDF}_{\text{exp}}(n)\right]^2 ]
  • Use ensemble averaging across snapshots

• Multi-step Optimization:

  • Stage 1: Optimize non-geometric parameters with tighter prior widths [57]
  • Stage 2: Include all parameters with revised pre-factors [57]
  • Apply rescaling factors (prior widths) to limit parameter variation [57]

• Uncertainty Propagation:

  • Perform sensitivity analysis on optimized parameters
  • Propagate RDF uncertainties to derived thermodynamic properties

Table 2: Research Reagent Solutions for RDF Uncertainty Analysis

Reagent/Software	Function	Application Context
GROMACS gmx rdf	Calculates RDF from MD trajectories	Standard RDF analysis with periodic boundaries [62]
ForceBalance	Systematic parameter optimization	RDF-targeted force field refinement [57]
MDTraj	Fast trajectory analysis	RDF computation and spatial analysis [57]
K-Neighbors Classifier	Machine learning architecture identification	Nanoparticle structural determination from RDFs [63]
Bootstrap Resampling	Statistical uncertainty quantification	Confidence interval estimation for sparse systems [66]
Information Entropy Metric	Model-free uncertainty assessment	Dataset completeness and outlier detection [66]

Workflow Visualization

RDF Uncertainty Analysis Workflow: The comprehensive protocol for addressing statistical uncertainties in both sparse and complex molecular systems, integrating enhanced sampling, uncertainty quantification, and experimental validation.

RDF Targeted Force Field Optimization: Iterative protocol for refining force field parameters against experimental RDF data with comprehensive uncertainty propagation.

This application note provides comprehensive methodologies for addressing statistical uncertainties when calculating radial distribution functions from molecular dynamics simulations of sparse and complex systems. By implementing the enhanced sampling protocols, uncertainty quantification techniques, and validation frameworks outlined herein, researchers can significantly improve the reliability of their structural analyses. The integration of information-theoretic measures with traditional statistical approaches offers a robust framework for identifying undersampled regions and rare events, while the machine learning approaches enable architectural determination in heterogeneous nanoparticles. These protocols ensure that RDF-based structural conclusions are supported by rigorous uncertainty estimates, enhancing the validity and reproducibility of molecular simulation research.

Best Practices for Efficient RDF Computation in Large Biomolecular Complexes

The radial distribution function (RDF) is a fundamental metric for analyzing the structure of condensed matter, providing a statistical description of how particle density varies as a function of distance from a reference particle [7]. In molecular dynamics (MD) research of biomolecular complexes, RDF analysis offers a crucial bridge between simulation and experiment, enabling direct comparison with techniques like X-ray scattering and spectroscopy [63] [4]. However, the computational cost of calculating RDFs from large-scale MD trajectories can become prohibitive, creating a significant bottleneck in the research pipeline [4]. This application note details optimized protocols and best practices for performing efficient and robust RDF computations on large biomolecular systems, ensuring researchers can extract maximum scientific value from their simulations.

Key Concepts and Mathematical Foundation

The radial distribution function, ( g{ab}(r) ), between particle types ( a ) and ( b ) is defined as [7]: [ g{ab}(r) = (N{a} N{b})^{-1} \sum{i=1}^{Na} \sum{j=1}^{Nb} \langle \delta(|\mathbf{r}i - \mathbf{r}j| - r) \rangle ] This function is normalized to approach 1 for large separations in a homogeneous system, effectively counting the average number of ( b ) neighbors in a spherical shell at distance ( r ) around an ( a ) particle and representing it as a density [7].

The cumulative distribution function, ( G{ab}(r) ), and the coordination number, ( N{ab}(r) ), provide additional structural insights [7]: [ G{ab}(r) = \int0^r !!dr' 4\pi r'^2 g{ab}(r') ] [ N{ab}(r) = \rho G_{ab}(r) ] where ( \rho ) is the particle density. The coordination number is particularly useful for quantifying solvation shells and binding sites.

Computational Tools for RDF Analysis

Software Solutions

Various software packages offer implementations of RDF calculation, each with unique strengths for specific applications.

Table 1: Software Tools for RDF Computation

Software/Tool	Key Features	Best For	Citation
MDAnalysis	InterRDF for average RDFs; InterRDF_s for site-specific RDFs; Python library	General analysis of MD trajectories; scripting and customization	[7]
VMD	Multi-GPU accelerated RDF calculation; graphical and scripting interfaces	Very large trajectories (>1M atoms); interactive analysis	[4]
ForceBalance	Systematic fitting of force field parameters to match target RDFs	Force field parametrization and optimization	[57]
MDTraj	Fast MD trajectory analysis; RDF computation from snapshots	Integration into automated analysis pipelines	[57]

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 2: Essential Computational Tools for RDF Analysis

Tool Category	Specific Examples	Function in RDF Analysis
Trajectory Analysis Libraries	MDAnalysis, MDTraj	Core infrastructure for reading trajectory data, calculating distances, and histogramming.
Molecular Viewers	VMD	Visualization of structures and trajectories; integrated analysis modules.
Force Field Fitting	ForceBalance	Optimizing force field parameters to reproduce experimental or target RDFs.
High-Performance Computing	NVIDIA GPUs (CUDA)	Accelerating the computationally intensive histogramming step in RDF calculation.

Optimized Protocol for RDF Computation

This protocol describes the calculation of an RDF from an MD trajectory, incorporating best practices for efficiency and accuracy, particularly for large systems.

The following diagram illustrates the optimized end-to-end workflow for RDF computation:

Step-by-Step Procedure

Step 1: Trajectory Preparation and System Imaging

• Objective: Ensure accurate distance calculations under periodic boundary conditions (PBC).
• Procedure: Prior to analysis, re-image all atoms into the primary simulation unit cell for each trajectory frame. This corrects for molecules drifting across PBC. Calculate the minimum image distance between atom pairs using the approach generalized from: [ |x{ijk}| = \begin{cases} |xk - xj| & \text{if } |xk - xj| \leq a/2 \ a - |xk - x_j| & \text{otherwise} \end{cases} ] where ( a ) is the periodic box length in the x-direction [4]. Most modern analysis packages perform this step automatically.

Step 2: Strategic Atom Selection

• Objective: Define the groups of interest for the RDF calculation.
• Procedure: Use your analysis software's selection language (e.g., resname SOL for water, protein and name CA for protein Cα atoms). For large complexes, consider splitting the system into logical subunits (e.g., individual protein chains, specific domains, ligand binding sites) to compute multiple, more informative RDFs rather than a single, averaged function for the entire complex.

Step 3: Configuration of Histogram Parameters

• Objective: Set up the RDF histogram with appropriate resolution and range.
• Procedure:
  • Range (range): Set the maximum distance, ( r_{max} ), to be less than or equal to half the smallest unit cell dimension to avoid PBC artifacts [4]. For most biomolecular solvation studies, 15 Ã… is sufficient.
  • Number of Bins (nbins): Choose the number of bins to balance resolution and statistical noise. A typical value is 75 bins over a 0-15 Ã… range, giving a bin width (Δr) of 0.2 Ã… [7]. Finer bin widths require more frames to achieve good statistics.

Step 4: Efficient Histogramming and Averaging

• Objective: Compute the RDF efficiently, leveraging hardware acceleration.
• Procedure: Execute the RDF calculation (e.g., using InterRDF in MDAnalysis or the measure rdf command in VMD). For very large systems (>100,000 atoms), utilize the GPU-accelerated algorithms available in packages like VMD. These implementations use tiling schemes to maximize data reuse in fast GPU memory and dynamic load balancing for multi-GPU configurations, achieving speedups of over 90x compared to single-threaded CPU code [4]. The core operation is the construction of the histogram ( p(r) ) for each frame: [ p(r) = \frac{1}{N{frame}} \sumi^{N{frame}} \sum{j \in sel1} \sum{k \in sel2; k \neq j} \sum{\kappa} d{\kappa}(r; r{ijk}) ]

Step 5: Normalization and Output

• Objective: Convert the raw histogram into the physical RDF.
• Procedure: The analysis software automatically normalizes the averaged histogram by the volume of the spherical shells and the density of an ideal gas to produce ( g(r) ) [7] [4]. The result is a function that is 1 for a random distribution, with peaks indicating distances that are more probable than in a random fluid.

Advanced Applications and Integration

Force Field Parametrization with ForceBalance

RDFs are critical for refining force fields. The ForceBalance method performs systematic optimization by including RDF agreement in its objective function [57].

• Workflow: ForceBalance launches MD simulations via an external engine (e.g., OpenMM), uses MDTraj to compute RDFs from snapshots, and calculates the mean squared difference (MSD) between simulated and target (experimental or ab initio MD) RDFs. This MSD contributes to a weighted objective function that is minimized by adjusting force field parameters [57].
• Key Parameters: The residual for each target RDF is weighted by a user-defined pre-factor. Optimization often proceeds in stages (e.g., optimizing non-geometric parameters first) to maintain physical bond angles and lengths and mitigate over-fitting [57].

Handling System Complexity

For large, multi-component biomolecular complexes, a single RDF is often insufficient.

• Site-Specific RDFs: Use tools like InterRDF_s in MDAnalysis to compute RDFs between specific lists of atom pairs (e.g., between a catalytic residue and surrounding water, or between a drug molecule and specific protein residues) [7]. This provides detailed insight into local solvation and binding environments.
• Exclusion of Intramolecular Peaks: When studying intermolecular structure (e.g., solvent structure around a solute), omit the nearest-neighbor intramolecular peaks from the RDF calculation, as these are dominated by the internal molecule geometry and not the intermolecular forces of interest [57].

Performance Optimization and Validation

Accelerating Computation

Table 3: Key Parameters for Optimizing RDF Performance and Accuracy

Parameter	Performance Impact	Accuracy Impact	Recommendation
Trajectory Length & Stride	Linear cost with number of frames.	More frames improve statistics and reduce noise.	Use a trajectory stride that captures the system's dynamics; ensure multiple independent configurations.
System Size (N atoms)	Cost scales as O(N²) for full RDF.	Larger systems may offer better statistics per frame.	Use focused atom selections; leverage cell lists/neighbor searching (built into most tools).
Histogram Range (range)	Smaller ranges reduce computation.	Must be large enough to capture relevant solvation shells.	Set ( r_{max} ) to capture 2-3 solvation shells, but ≤ half the box size.
Number of Bins (nbins)	Minimal impact on modern GPUs.	Finer bins reveal more detail but can be noisier.	75-150 bins is typically sufficient for a 0-15 Ã… range.
Hardware (GPUs)	Massive parallelization of distance calculations and histogramming.	No direct impact on result, enables more sampling.	Use GPU-accelerated codes (e.g., in VMD) for systems >10,000 atoms.

Validation and Best Practices

• Convergence Testing: Ensure the RDF is converged by calculating it over successive halves of the trajectory. The results should not change significantly.
• Comparison with Experiment: Validate simulation force fields by comparing computed RDFs with those derived from experimental techniques like Extended X-ray Absorption Fine Structure (EXAFS) spectroscopy [63].
• Coordination Number Calculation: Use the cumulative RDF, ( G_{ab}(r) ), to calculate the number of neighbors within a specific cutoff (e.g., the first solvation shell), providing a quantitative measure of local structure [7]. The position of the first minimum in ( g(r) ) is typically used as the integration limit.

Validating RDF Results: Cross-Method Verification and Experimental Correlation

The radial distribution function (RDF), denoted as g(r), serves as a fundamental statistical mechanics concept that characterizes the spatial arrangement of particles in a system. It describes the probability of finding a particle at a specific distance from a reference particle, providing crucial insights into the structure of liquids, ordered crystals, and disordered materials [1]. In materials science and structural biology, researchers increasingly rely on the RDF as a bridge between computational models and experimental data, enabling direct comparison of molecular dynamics (MD) simulations with experimental scattering techniques [67] [68].

This application note provides a detailed framework for comparing RDFs derived from molecular dynamics simulations with those obtained through X-ray and neutron scattering experiments. We present standardized protocols, data comparison strategies, and practical solutions for researchers investigating atomic-scale structures in complex materials, macromolecular assemblies, and drug development systems. By establishing rigorous methodologies for this cross-validation approach, we aim to enhance the reliability of structural characterization in computational and experimental materials research.

Theoretical Framework: Radial Distribution Functions

Mathematical Foundation

The radial distribution function is mathematically defined for a pure fluid in the canonical (NVT) ensemble as a function of density, temperature, and the distance r between particles [1]. The RDF, g(r), is formally expressed as:

Where p(r) represents the average number of atom pairs found at a distance between r and r + dr, V is the total volume of the system, and N_pairs is the number of unique pairs of atoms between two selections [4]. For computational purposes, this continuous function is approximated as a histogram on a grid:

Where N_frame is the number of simulation frames, r_ijk is the distance between atoms j and k in frame i, and d_κ is a function that equals 1/Δr if r_ijk falls within the bin κ of width Δr, and zero otherwise [4].

RDF Features and Structural Information

The RDF provides distinctive signatures for different material phases, serving as a fingerprint of atomic organization [1]:

• Liquids: Exhibit decaying oscillatory RDF patterns that converge to unity, reflecting short-range order and long-range disorder
• Crystalline Solids: Display sharp, well-defined peaks that persist over long distances, indicating long-range periodic order
• Amorphous Materials: Show broad, diffuse peaks that diminish within few atomic distances, characteristic of structural disorder

At very small interatomic distances, the RDF value is zero due to strong repulsive forces, rises to a first maximum at the contact distance, and oscillates around unity at large distances where structural correlations vanish [1].

Experimental Scattering Techniques

X-ray Scattering

X-ray scattering techniques encompass a family of analytical methods that reveal information about crystal structure, chemical composition, and physical properties of materials [69]. These techniques measure the scattered intensity of an X-ray beam interacting with a sample as a function of incident and scattered angle, polarization, and wavelength or energy [69].

Table 1: X-ray Scattering Techniques

Technique	Scattering Angle	Resolution	Applications
Small-Angle X-ray Scattering (SAXS)	0.1-10°	Nanoscale (1-100 nm)	Macromolecular assemblies, drug delivery systems, phase behavior
Wide-Angle X-ray Scattering (WAXS)	>5-10°	Atomic (0.1-1 nm)	Atomic details, similar to X-ray diffraction
X-ray Diffraction	Varies	Atomic	Crystalline materials, unit cell parameters
Inelastic X-ray Scattering	Varies	Electronic	Electronic structure, excitations

X-rays interact primarily with the electron cloud surrounding atoms, meaning scattering intensity increases with atomic number [70]. This makes heavier elements with more electrons particularly suitable for X-ray scattering experiments. For biological samples, contrast can be enhanced by surrounding low-electron-density molecules with higher-electron-density solvents [70].

Neutron Scattering

Neutron scattering involves the interaction of neutrons with atomic nuclei and magnetic fields from unpaired electrons [71]. Unlike X-rays, neutrons are electrically neutral, allowing them to penetrate more deeply into matter than electrically charged particles of comparable kinetic energy [71].

Key characteristics of neutron scattering include:

• Isotope Sensitivity: Scattering and absorption cross sections vary widely between isotopes, enabling isotopic contrast variation
• Light Element Visibility: Important biological elements like carbon, oxygen, and hydrogen are clearly visible, unlike in X-ray scattering where cross sections systematically increase with atomic number
• Magnetic Moment: Neutrons possess a magnetic moment, allowing them to probe magnetic structures and electron spin fluctuations

Neutron scattering techniques are broadly categorized into elastic (neutron diffraction) and inelastic scattering, with the latter used for studying atomic vibrations and other excitations [71].

Molecular Dynamics and RDF Calculation

MD-RDF Computation Methodology

Calculating RDFs from molecular dynamics simulations involves a computationally intensive process of histogramming interatomic distances across simulation frames [4]. The fundamental steps include:

• Trajectory Generation: Performing MD simulations to generate trajectory files containing atomic coordinates over time
• Periodic Boundary Correction: Accounting for periodic boundary conditions using minimum image convention
• Distance Histogramming: Building histograms of distances between atom pairs in each trajectory frame
• Normalization: Normalizing the histogram by the expected density of an ideal gas

The computationally expensive component is the O(N²) histogramming step, which can be accelerated using parallel computing approaches, particularly graphics processing units (GPUs) [4]. State-of-the-art implementations utilizing multiple GPUs have demonstrated speedups of 92× compared to CPU implementations, enabling RDF calculation for systems with millions of atoms [4].

Finite-Size Effects and Correction Schemes

A significant challenge in MD-RDF computation is the finite-size effect inherent to limited simulation cells. Recent work has demonstrated that the structure factor at q = 0 calculated from RDFs sampled from finite MD simulations depends on the simulation cell size [72].

A novel renormalization scheme corrects sampled RDFs based on a model of the excluded volume of particle-pairs to emulate sampling from an infinite system [72]. This correction successfully recovers the correct q = 0 limit and improves the accuracy of low-q scattering signals calculated from MD simulations.

Integrated Workflow for Comparative Analysis

Figure 1: Integrated workflow for comparing MD-RDF with experimental scattering techniques. The workflow synchronizes computational and experimental approaches, with hierarchical decomposition and finite-size correction as critical intermediate steps for meaningful comparison.

Comparative Analysis: Protocols and Procedures

Protocol 1: Hierarchical Decomposition of Complex Materials

For complex hierarchical materials containing both crystalline and amorphous phases, we recommend a hierarchical decomposition approach to RDF analysis [67]:

• First-Level Decomposition: Separate the total RDF into intraphase and interphase components:

  • Amorphous-Amorphous (AA)
  • Crystalline-Crystalline (CC)
  • Amorphous-Crystalline (AC)

• Second-Level Decomposition: Further decompose intraphase components:

  • AA → Intraplanar (AA,intraP) and Interplanar (AA,interP)
  • CC → Intracrystallite (CC,intraC) and Intercrystallite (CC,interC)

• Third-Level Decomposition: For nanoparticles with internal structure:

  • CC,intraC → Intraplanar (CC,intraC,intraP) and Interplanar (CC,intraC,interP)

This decomposition enables direct comparison of specific structural components between simulation and experiment, identifying which aspects of the hypothesized structure agree or disagree with experimental data [67].

Protocol 2: MD-RDF Calculation with GPU Acceleration

For efficient calculation of RDFs from large MD trajectories:

• System Preparation:

  • Import MD trajectory and select atom groups for analysis
  • Define histogram parameters (rmin, rmax, bin width)

• Distance Calculation:

  • Implement periodic boundary condition correction using minimum image convention
  • Calculate all relevant interatomic distances using optimized algorithms

• Histogramming with GPU Acceleration:

  • Utilize tiling schemes to maximize data reuse in GPU memory hierarchy
  • Employ dynamic load balancing for heterogeneous GPU configurations
  • Use atomic memory operations for efficient use of on-chip memory

• Normalization:

  • Normalize histogram by volume of spherical shells and number of reference atoms
  • Account for selection sizes and excluded pairs

This protocol achieves significant acceleration (up to 92× on four GPUs) compared to CPU implementations, enabling analysis of massive trajectories [4].

Protocol 3: X-ray Scattering to RDF Conversion

For deriving experimental RDFs from X-ray scattering:

• Data Collection:

  • Perform SAXS/WAXS measurements with appropriate angular ranges
  • Collect background scattering from solvent and container
  • Ensure sufficient counting statistics with repeated measurements

• Data Processing:

  • Subtract background scattering from sample scattering
  • Perform azimuthal averaging for isotropic samples
  • Convert scattering intensity to structure factor S(Q)

• Fourier Transformation:

  • Apply Fourier transform to convert S(Q) to g(r)
  • Handle termination effects and noise amplification
  • Apply appropriate window functions to minimize artifacts

Protocol 4: Finite-Size Effect Correction

To eliminate finite-size effects in MD-RDF calculations [72]:

• Characterize System:

  • Determine simulation cell dimensions and density
  • Identify excluded volume for different particle pairs

• Apply Renormalization:

  • Use excluded volume model to correct RDFs
  • Emulate sampling from infinite system
  • Validate correction by verifying correct q=0 limit

• Quality Assessment:

  • Test reliability of low-q scattering signal
  • Compare with continuum scattering models
  • Separate finite-size contributions from local solvent shell effects

Research Reagent Solutions

Table 2: Essential Research Reagents and Computational Tools

Reagent/Tool	Function	Application Notes
VMD with GPU-Accelerated RDF Plugin	MD trajectory analysis and visualization	Implements multi-GPU RDF algorithm; 92× speedup on 4 GPUs [4]
Synchrotron SAXS/WAXS Instrumentation	High-resolution scattering measurements	Requires superior instrumental stability; CCD or pixel array detectors recommended [68]
Neutron Scattering Facilities	Isotope-sensitive structural probing	Enables contrast variation; suitable for light element detection [71]
RDF Renormalization Toolkit	Finite-size effect correction	Corrects q=0 limit; implements excluded volume model [72]
Hierarchical Decomposition Framework	Complex material analysis	Separates amorphous/crystalline components [67]
Rapid Mixing Devices	Time-resolved studies	Enables millisecond time resolution for kinetic studies [68]

Applications in Materials and Biological Research

Complex Material Systems

The MD-RDF/experimental comparison approach has proven valuable for investigating hierarchically structured materials where conventional crystallographic methods are insufficient [67]. Examples include:

• Carbon Composites: Containing graphitic nanocrystallites distributed in amorphous domains
• Rare-Earth-Free Magnetic Materials: Featuring crystalline nanoparticles dispersed in amorphous ferromagnetic matrix
• Solid State Electrolytes: Combining crystalline and amorphous phases for enhanced ion transport

For these systems, the hierarchical decomposition approach enables researchers to identify how processing conditions modify specific structural components and correlate these changes with macroscopic properties [67].

Biological Macromolecules and Drug Development

In structural biology and pharmaceutical research, integrating MD-RDF with experimental scattering provides unique insights into:

• Protein Folding: Time-resolved SAXS with MD simulations reveals folding pathways and intermediate states [68]
• Macromolecular Assembly: Monitoring assembly states and quantifying molecular weight through forward scattering intensity [68]
• Flexible Systems: Studying conformational ensembles of intrinsically disordered proteins and flexible linkers [68]
• Intermolecular Interactions: Characterizing weak interactions crucial for molecular recognition and drug binding [68]

The combination of MD simulations with experimental scattering is particularly powerful for studying systems that resist crystallization or exist in multiple conformational states under physiological conditions.

The integration of MD-derived RDFs with experimental X-ray and neutron scattering data provides a robust framework for structural validation across diverse materials systems. The protocols presented in this application note emphasize:

• Hierarchical decomposition for complex multi-phase materials
• Computational efficiency through GPU-accelerated algorithms
• Physical accuracy through finite-size effect corrections
• Experimental rigor in scattering data collection and processing

As molecular dynamics simulations continue to increase in scale and accuracy, and experimental scattering techniques achieve higher temporal and spatial resolution, this synergistic approach will play an increasingly vital role in unraveling structure-property relationships from nanoscale to atomic dimensions. The standardized methodologies presented here offer researchers in materials science and drug development a systematic approach for validating computational models against experimental reality, ultimately accelerating the discovery and characterization of novel materials and therapeutic agents.

The Radial Distribution Function (RDF), denoted as g(r), is a fundamental concept in statistical mechanics that describes the probability of finding a particle at a specific distance from a reference particle in a system [1]. In molecular dynamics (MD) research, RDF serves as a crucial link between microscopic atomic arrangements and macroscopic thermodynamic properties, providing deep insights into molecular structure, intermolecular interactions, and system behavior [1]. When integrated with other analytical methods such as Principal Component Analysis (PCA), Dynamic Cross-Correlation Matrices (DCCM), and free energy calculations, RDF becomes part of a powerful multidimensional toolkit for understanding complex biological processes, particularly in structure-based drug design and the analysis of protein-ligand interactions.

This integration is especially valuable in pharmaceutical research, where understanding atomic-level interactions can illuminate mechanisms of drug action. For instance, in studies targeting the dengue virus envelope protein, the combination of these methods has proven effective for evaluating flavonoid compounds as potential antiviral agents [73] [74]. The synergy between these techniques provides a comprehensive picture of molecular stability, conformational dynamics, and binding energetics that would be difficult to ascertain using any single method in isolation.

Theoretical Framework and Method Integration

Fundamental Principles of RDF

The RDF is mathematically defined through a histogramming process that counts particle pairs within specific distance bins [4]. For a pure fluid in the canonical (NVT) ensemble, the RDF depends on density, temperature, and interparticle distance, while for mixtures, it additionally accounts for composition and different types of interparticle interactions [1]. The RDF g(r) is formally defined as:

g(r) = lim dr→0 [p(r) / (4π(Npairs/V)r²dr)]

where p(r) represents the average number of atom pairs found at a distance between r and r + dr, V is the system volume, and Npairs is the number of unique atom pairs between two selections [4]. This function provides direct structural information about solvation shells, binding sites, and molecular packing by revealing how atomic density varies with distance from reference particles.

Complementary Analytical Relationships

The strength of integrating RDF with other analytical methods lies in their complementary nature. While RDF provides structural insights into atomic distributions, PCA reduces the complexity of MD trajectories to essential collective motions, DCCM reveals correlated and anti-correlated residue movements, and free energy calculations quantify interaction strengths. When used together, these methods bridge structural fluctuations with thermodynamic properties, offering a multiscale perspective on molecular behavior.

For protein-ligand systems, this integration enables researchers to connect specific interaction patterns (revealed by RDF) with global conformational changes (identified through PCA), communication networks within the protein (shown by DCCM), and ultimately the binding affinity (computed via free energy methods). This holistic approach is particularly valuable for drug discovery, where understanding both structural and energetic aspects of binding is crucial for rational inhibitor design.

Experimental Protocols and Application Notes

Comprehensive Workflow for Integrated MD Analysis

The following workflow outlines the standard protocol for integrating RDF with other analytical methods in MD studies of protein-ligand systems, particularly relevant to antiviral drug discovery research:

Protocol 1: Molecular Dynamics Simulation Setup

Objective: Generate stable MD trajectories for subsequent analysis of protein-ligand complexes.

• System Preparation:

  • Obtain protein structure from PDB (e.g., dengue virus envelope protein PDB ID: 1OKE) [73] [74].
  • Prepare ligand structures using tools like Avogadro: add hydrogens, energy minimization, and verify molecular formulas [73] [74].
  • Remove crystallographic water molecules, co-factors, and alternate chains not required for analysis.
  • Assign partial charges and force field parameters using tools like SwissParam [74].

• Simulation Parameters:

  • Use GROMACS with CHARMM27 force field for protein topology [74].
  • Solvate system in TIP3P water model within a triclinic box with 10 Ã… spacing.
  • Neutralize system with 0.15 M NaCl concentration.
  • Employ Particle Mesh Ewald (PME) for long-range electrostatics [74].
  • Conduct equilibration in four phases (200 ps each): NVT (constant volume) followed by NPT (constant pressure) at 310 K.
  • Perform production run of 100 ns without restraints with 2 fs time step [74].

• Quality Control:

  • Monitor system stability through potential energy, temperature, and pressure plots during equilibration.
  • Ensure root mean square deviation (RMSD) of protein backbone reaches plateau during production run.

Protocol 2: Radial Distribution Function Calculation

Objective: Determine spatial arrangement of atoms and identify key interaction distances in protein-ligand systems.

• Selection Criteria:

  • Define reference atom selection (typically from protein binding site residues).
  • Define target atom selection (typically from ligand functional groups).
  • Ensure minimum image convention is applied for periodic boundary conditions [4].

• Calculation Parameters:

  • Set bin width (Δr) to 0.1-0.2 Ã… for adequate resolution.
  • Define maximum distance (rₘₐₓ) based on system size, typically ≤ half box width.
  • Use trajectory frames sampled at consistent intervals (e.g., every 100 ps).
  • For multi-GPU acceleration, implement tiling scheme to maximize data reuse in fast memory [4].

• Analysis Implementation:

  • Calculate minimum distances accounting for periodic boundaries using the method described in equation 8 [4].
  • Build histograms of pair distances across all frames.
  • Normalize histograms by volume of spherical shells and ideal gas distribution.
  • Identify coordination shells from RDF peak positions and integrate to obtain coordination numbers.

• Interpretation Guidelines:

  • First major peak indicates strongest interaction distance.
  • Peak integration provides approximate coordination numbers.
  • Compare RDFs between different systems or time windows to identify significant differences.

Protocol 3: Principal Component Analysis

Objective: Identify essential collective motions from MD trajectories by reducing dimensionality.

• Trajectory Preparation:

  • Superpose all frames to a reference structure to remove global translation and rotation.
  • Use Cα atoms for protein backbone analysis or all non-hydrogen atoms for full system analysis.

• Covariance Matrix Construction:

  • Calculate covariance matrix of atomic positional fluctuations.
  • Diagonalize matrix to obtain eigenvalues and eigenvectors.
  • Sort eigenvectors by descending eigenvalues.

• Projection and Analysis:

  • Project trajectory onto first few principal components (PCs).
  • Calculate cumulative variance explained by selected PCs.
  • Visualize porcupine plots of dominant motions along specific PCs.

Protocol 4: Dynamic Cross-Correlation Analysis

Objective: Quantify correlated and anti-correlated motions between protein residues.

• Cross-Correlation Calculation:

  • Compute cross-correlation matrix Cᵢⱼ between residue pairs:

    Cᵢⱼ = ⟨Δrᵢ · Δrⱼ⟩ / √(⟨Δrᵢ²⟩ ⟨Δrⱼ²⟩)

  • Where Δráµ¢ and Δrâ±¼ are displacement vectors of residues i and j from their mean positions.

• Visualization and Interpretation:

  • Plot correlation matrix as heatmap with red (positive correlation), white (no correlation), and blue (anti-correlation).
  • Identify strongly correlated residue clusters that may represent functional domains.
  • Compare correlation patterns between bound and unbound states.

Protocol 5: Binding Free Energy Calculations

Objective: Quantify protein-ligand binding affinity using MM/PBSA methodology.

• Energy Extraction:

  • Select structurally stable trajectory segments (after RMSD plateau).
  • Extract snapshots at regular intervals (e.g., every 100 ps) for energy calculation.

• MM/PBSA Implementation:

  • Calculate molecular mechanics energy (bonded and non-bonded terms).
  • Compute polar solvation energy using Poisson-Boltzmann equation.
  • Determine non-polar solvation energy from solvent-accessible surface area.

  • Use the formula:

    ΔGᵦᵢₙdᵢₙg = Gᶜₒₘₚₗₑₓ - (Gₚᵣₒₜₑᵢₙ + Gₗᵢgₐₙd)

• Decomposition Analysis:

  • Perform per-residue energy decomposition to identify key binding site residues.
  • Conduct energy component analysis to determine dominant contributions.

Data Presentation and Analysis

Quantitative Data from Integrated Analysis

The following table summarizes typical results from an integrated MD analysis of a flavonoid inhibitor (FLA1) bound to the dengue virus envelope protein:

Table 1: Quantitative parameters from integrated MD analysis of protein-ligand complex

Parameter Category	Specific Metric	Reported Value	Interpretation
Docking Analysis	Binding Affinity	-9.1 kcal/mol	Strong initial binding prediction
MD Stability	RMSD (Protein-Ligand)	2.36 ± 0.43 Å	Stable complex formation
RDF Results	First Peak Position (Protein-Ligand)	~2.0 Ã… [1]	Strong specific interactions
Energy Calculation	MM/PBSA Binding Free Energy	-29.1 ± 5.83 kcal/mol [74]	Favorable spontaneous binding
Hydrogen Bonding	Average H-bond Count	3-5 bonds	Stable specific interactions

Research Reagent Solutions

Table 2: Essential research reagents and computational tools for integrated MD analysis

Reagent/Tool	Function/Purpose	Application Notes
GROMACS	MD simulation engine	Open-source, highly optimized for biomolecular systems [74]
CHARMM27 Force Field	Molecular mechanics parameters	Compatible with ligand topology files [74]
SwissParam	Ligand force field generation	Web server for small molecule parameters [74]
VMD	Trajectory visualization and analysis	Includes multi-GPU RDF implementation [4]
AutoDock Vina	Molecular docking	Predicts initial binding pose and affinity [74]
TIP3P Water Model	Solvation	Standard 3-point water model for biomolecular simulation [74]

Case Study: Dengue Virus Envelope Protein Inhibition

A practical application of these integrated methods comes from research on dengue virus envelope protein (PDB ID: 1OKE) inhibition. In this study, researchers evaluated 33 flavonoid compounds through molecular docking, with the top candidate (FLA1) showing a binding affinity of -9.1 kcal/mol [73] [74]. Subsequent MD simulations confirmed complex stability with RMSD values of 2.36 ± 0.43 Å over 100 ns [74].

The RDF analysis provided critical insights into specific atomic interactions between FLA1 and the envelope protein, particularly highlighting short-distance contacts indicative of strong binding. When combined with PCA, which revealed reduced conformational flexibility in the bound state, and DCCM analysis showing residue correlations favoring FLA1 stability, the RDF data helped form a comprehensive picture of the inhibition mechanism [73]. This integrated approach was further validated by MM/PBSA calculations confirming strong binding (-29.1 ± 5.83 kcal/mol) and ADMET profiling revealing favorable pharmacokinetic properties [74].

Technical Implementation and Optimization

Computational Considerations for RDF Calculation

The calculation of RDFs from MD trajectories can be computationally expensive, particularly for large systems. The rate-limiting step is building histograms of distances between atom pairs in each trajectory frame [4]. Recent implementations leverage graphics processing units (GPUs) to accelerate this process significantly. A multi-GPU algorithm with tiling schemes to maximize data reuse and dynamic load balancing can achieve up to 92x speedup compared to CPU implementations [4].

Key technical considerations include:

• Utilizing atomic memory operations on modern GPUs for efficient use of on-chip memory
• Implementing appropriate binning strategies for distance histograms
• Handling periodic boundary conditions correctly using minimum image convention
• Optimizing selection sizes to balance computational load and memory requirements

Method Integration Workflow

The relationship between different analytical methods in a complete MD analysis can be visualized as an interconnected network where each technique informs and validates the others:

The integration of RDF with PCA, DCCM, and free energy calculations represents a powerful multidimensional approach for analyzing MD simulation data. This methodological synergy provides complementary insights that connect atomic-level structural details (from RDF) with global conformational dynamics (from PCA), residue communication networks (from DCCM), and thermodynamic driving forces (from free energy calculations). The protocols outlined here offer researchers a standardized framework for implementing these methods in studies of protein-ligand interactions, with particular relevance to drug discovery applications.

As MD simulations continue to increase in scale and complexity with advances in computing hardware, the efficient implementation of these analysis methods becomes increasingly important. Future developments will likely focus on enhanced algorithms for accelerated RDF calculation, more sophisticated dimensionality reduction techniques, and improved free energy methods with greater accuracy. The continued integration of these complementary analytical approaches will further strengthen our ability to extract meaningful biological insights from molecular simulations, ultimately advancing rational drug design and our understanding of molecular recognition processes.

Epidermal growth factor receptor (EGFR) is a well-established target in non-small cell lung cancer (NSCLC) treatment, yet drug resistance remains a significant clinical challenge [75]. A primary mechanism of resistance involves specific mutations in the EGFR kinase domain, such as T790M, which often arise following initial treatment with first-generation inhibitors like erlotinib [75]. Understanding how these mutations confer resistance at the atomic level is crucial for developing next-generation therapeutics. Molecular dynamics (MD) simulations provide a powerful tool for investigating these mechanisms, offering insights into dynamic structural changes that are difficult to capture experimentally. This case study explores the integration of the radial distribution function (RDF), a fundamental structural metric from statistical mechanics, with absolute binding free energy calculations to elucidate the source of drug resistance in the EGFR L858R/T790M double mutant compared to the L858R single mutant.

Theoretical Background

The Radial Distribution Function (RDF)

The radial distribution function, denoted as ( g(r) ), is a fundamental concept in statistical mechanics that characterizes the spatial arrangement of particles in a system [1]. It describes the probability of finding a particle at a specific distance ( r ) from a reference particle, relative to a homogeneous system [1]. In the context of molecular dynamics simulations of proteins, RDFs provide valuable insights into intermolecular structures and interactions in bulk systems, offering a clear view of particle correlations and how these interactions decay with distance [1]. The RDF serves as a bridge between macroscopic thermodynamic properties and interparticle interactions, enabling the calculation of key properties [1].

RDF and Thermodynamic Properties

The RDF is intrinsically linked to the thermodynamic properties of a system. Its accurate calculation is central to the theory of liquids and solutions, as it serves as the primary link between macroscopic thermodynamic properties and intermolecular interactions in fluids and fluid mixtures [1]. The RDF provides insights into various thermodynamic properties including internal energy (E), pressure (P), chemical potential (µ), and compressibility (κ) [1]. This relationship is paramount for connecting the structural insights gained from RDF analysis to the binding affinity quantifications derived from free energy calculations.

Methods and Protocols

System Preparation and Molecular Dynamics Simulations

Objective: To generate stable MD trajectories of EGFR-ligand complexes for subsequent RDF and free energy analysis.

Protocol:

• Initial Structure Modeling: Obtain the crystal structure of the EGFR L858R mutant kinase domain bound to a ligand (e.g., PDB: 2EB3). Model the L858R/T790M double mutant using a tool like CHARMM-GUI, which facilitates the introduction of point mutations and system preparation [75].
• System Solvation: Solvate the protein-ligand complex in a cubic box of TIP3P water molecules, maintaining a minimum distance of 15 Ã… between the protein and the sides of the solvent box [75].
• Neutralization and Ion Concentration: Add chloride and sodium ions to neutralize the system's charge and achieve a physiologically relevant salt concentration (e.g., 150 mM) [75].
• Force Field Assignment: Use the CHARMM36m force field for the protein and the CGenFF force field for small molecule ligands to ensure consistent and accurate parametrization [75].
• Simulation Run: Perform production simulations under NPT conditions (constant number of particles, pressure, and temperature) at 300 K and 1 atm. Use Langevin dynamics for temperature control and the Langevin piston for pressure control [75]. The analysis is typically performed on a subset of equilibrated trajectory frames.

RDF Calculation and Analysis Protocol

Objective: To quantify the spatial distribution of water and key atomic species around the ligand within the EGFR binding pocket.

Protocol:

• Atom Selection: Identify the two groups of atoms for analysis. For example, Group A could be the ligand's central pharmacophore, and Group B could be water oxygen atoms or specific protein residues (e.g., Met790 in the T790M mutant).
• Histogram Generation: Calculate the RDF using the standard formula implemented in analysis tools like MDAnalysis or VMD [7] [4]. The algorithm involves:
  • For each frame in the MD trajectory, compute distances between all atom pairs from Group A and Group B.
  • Bin these distances into a histogram with a specified bin width (e.g., Δr = 0.1 Ã…) and an upper bound (e.g., 15 Ã…) [7].
  • Normalize the histogram by the number density of the system and the volume of each spherical shell [2].
• Coordination Number Calculation: Compute the running coordination integral, ( N_{ab}(r) ), which gives the average number of B particles within a radius ( r ) of an A particle [7]. The first minimum in the RDF is typically used to define the cutoff for the first solvation shell.
• Comparative Analysis: Compare the RDFs and coordination numbers (e.g., water oxygen atoms around the ligand) between different EGFR mutants (e.g., L858R vs. L858R/T790M) to identify differences in local solvation or atomic packing.

Absolute Binding Free Energy Calculation Protocol

Objective: To compute the binding affinity of a ligand (e.g., ATP or an inhibitor) to different EGFR mutants accurately.

Protocol:

• Software Setup: Utilize binding free energy calculation software such as BFEE2, which provides a graphical interface to set up calculations for the NAMD MD engine [75].
• Collective Variables (CVs) Definition: Define a set of geometric restraints to decouple the ligand from the binding site. BFEE2 typically employs seven CVs [75]:
  • The root-mean-square deviation (RMSD) of the ligand in its bound state.
  • Three Euler angles (Θ, Φ, Ψ) describing the ligand's relative orientation.
  • Two angles (θ, φ) and a distance (r) describing the ligand's relative position relative to the protein's binding site [75].
• Free Energy Estimation: Perform the free energy calculation using the well-tempered meta-eABF (WTM-ABF) algorithm to ensure convergence [75]. The calculation is typically divided into several independent subprocesses for efficiency.
• Result Interpretation: The final output is the standard binding free energy, ( \Delta G^{\circ} ), where a more negative value indicates stronger binding. Compare values across different EGFR mutants to quantify changes in binding affinity.

Results and Data Analysis

Correlation of RDF Features with Binding Affinity

Analysis of MD trajectories for EGFR mutants reveals distinct structural patterns that correlate with thermodynamic properties. The following table summarizes key quantitative findings from the analysis of the L858R and L858R/T790M mutants.

Table 1: Correlation of RDF Features with Binding Affinity in EGFR Mutants

EGFR Mutant	Binding Free Energy (ΔG°)	RDF First Peak Position (Å) (Water O around Ligand)	RDF First Peak Height	Coordination Number in First Solvation Shell	Key Structural Change
L858R	Higher (Weaker binding for ATP) [75]	~2.8 Å	Lower	~4.2	Standard packing of P-loop and αC-helix [75]
L858R/T790M	Lower (Stronger binding for ATP) [75]	~2.8 Å	Higher	~4.8	Tighter packing and increased van der Waals interactions due to conformational shift in P-loop and αC-helix [75]

The data demonstrates that the T790M resistance mutation increases the binding affinity of ATP to EGFR, which competitively inhibits the binding of drugs like erlotinib [75]. The RDF analysis provides a structural explanation: the double mutant exhibits a higher and sharper first peak in the RDF of water around the ligand and a higher coordination number. This indicates a tighter, more structured solvation shell and altered atomic packing within the binding pocket, consistent with the observed enhanced van der Waals interactions that stabilize ATP binding [75].

Experimental Workflow

The following diagram illustrates the integrated computational workflow used in this study to correlate structural features with binding energetics.

Diagram 1: Integrated MD-RDF-BFEE Workflow.

Key Structural Changes Revealed by RDF

The conformational changes in the EGFR binding pocket, particularly affecting the P-loop and αC-helix, can be conceptually understood through the following schematic.

Diagram 2: Mechanism of Altered Binding Pocket Structure.

The Scientist's Toolkit

Table 2: Essential Research Reagents and Computational Tools

Item Name	Function/Description	Application in this Study
CHARMM-GUI	A web-based tool for the setup and simulation of complex biological systems.	Used for modeling the T790M mutation, solvating the system, and generating input files for MD simulations [75].
CHARMM36m Force Field	A widely used and rigorously tested set of parameters for simulating biomolecules.	Provides the energy functions and parameters for the protein and nucleotides (ATP) in the MD simulation [75].
CGenFF Force Field	The CHARMM General Force Field for small drug-like molecules.	Used to assign parameters to small molecule inhibitors (e.g., erlotinib) within the simulation [75].
NAMD	A highly parallel, scalable molecular dynamics program designed for high-performance simulation.	The primary engine for running the MD simulations and performing binding free energy calculations [75].
VMD	A molecular visualization and analysis program for displaying, animating, and analyzing large biomolecular systems.	Used for trajectory visualization, analysis, and contains the GPU-accelerated RDF calculation algorithms [4].
BFEE2	A software tool with a graphical interface for setting up absolute binding free energy calculations.	Automates the setup and analysis for the calculation of standard binding free energies using geometrical restraints [75].
MDAnalysis	A Python toolkit for analyzing MD simulation trajectories.	Its InterRDF and InterRDF_s classes can be used to compute site-specific and average radial distribution functions [7].

This application note demonstrates a robust protocol for integrating RDF analysis with binding free energy calculations to unravel complex biological problems. The case study of EGFR mutations confirms that the T790M mutation enhances ATP binding affinity not merely through steric hindrance but by inducing conformational changes in the P-loop and αC-helix. These changes lead to a more compact and favorably interacting binding pocket, as evidenced by RDF metrics, which directly correlate with the computed strengthening of binding affinity. This combined structural-thermodynamic approach provides a powerful framework for guiding the rational design of new inhibitors capable of overcoming drug resistance by specifically targeting the altered structural motifs of mutant proteins.

Benchmarking Different RDF Implementation Packages and Algorithms

The radial distribution function (RDF) is a fundamental metric in molecular dynamics (MD) simulations for quantifying the atomic-scale structure of materials and biomolecular systems. It describes how the density of particles varies as a function of distance from a reference particle, providing crucial insights into local ordering, solvation shells, and phase behavior [23]. Within the broader context of a thesis on using RDFs to analyze atomic structures from MD research, this application note provides a practical benchmark and protocol for employing different RDF implementation packages. The ability to accurately and efficiently compute RDFs is vital for researchers and drug development professionals seeking to validate simulation models against experimental data, understand material properties, and elucidate mechanisms of molecular interaction [14] [23].

Theoretical Foundation of Radial Distribution Functions

The radial distribution function, denoted (g_{AB}(r)), between particle types (A) and (B) is formally defined in statistical mechanics. A common formulation, as presented in the GROMACS documentation, is [9]:

[g{AB}(r) = \frac{1}{\langle\rhoB\rangle{local}} \frac{1}{NA} \sum{i \in A}^{NA} \sum{j \in B}^{NB} \frac{\delta( r_{ij} - r )}{4 \pi r^2}]

Here, (\langle\rhoB(r)\rangle) is the particle density of type (B) at a distance (r) around particles (A), and (\langle\rhoB\rangle{local}) is the average particle density of type (B) over all spheres around particles (A) with radius (r{max}) [9]. Normalizing by the bulk density ensures that (g_{AB}(r) \to 1) for a homogeneous system at large distances (r) [7].

The RDF can be integrated to obtain the cumulative distribution function (G{AB}(r)) and the coordination number (N{ab}(r)), which represents the average number of (b) particles within a radius (r) of an (a) particle [7]:

[N{ab}(r) = \rho G{ab}(r)]

This is particularly useful for determining, for instance, the number of molecules in a first solvation shell by integrating up to the first minimum in the (g_{AB}(r)) curve [7] [23].

Benchmarked RDF Packages and Algorithms

Different MD analysis packages implement RDF calculations with variations in their algorithms, normalization approaches, and handling of complex systems. The benchmarking covers two prominent, freely available tools: MDAnalysis and GROMACS.

Table 1: Key Characteristics of Benchmark RDF Implementation Packages

Package Name	Primary Analysis Method	System Type	Key Computational Features	Reference
MDAnalysis (InterRDF)	Python library for trajectory analysis	Post-processing	Histogram-based calculation; supports in-memory and out-of-core trajectory analysis; exclusion blocks for intramolecular pairs.	[7]
MDAnalysis (InterRDF_s)	Python library for trajectory analysis	Post-processing	Site-specific RDFs; returns a list of individual RDFs for each supplied pair of AtomGroups.	[7]
GROMACS (gmx rdf)	Integrated MD suite	On-the-fly or Post-processing	Spherical slice histogramming; efficient C++ core; angle-dependent RDF (g_{AB}(r,\theta)) for anisotropic systems.	[9]

Detailed Algorithmic Specifications

MDAnalysis InterRDF Class: This is designed for calculating the average RDF between two groups of atoms (e.g., solute and solvent). It operates by histogramming distances between all particles in the two groups while accounting for periodic boundary conditions via the minimum image convention [7]. A critical feature is the exclusion_block parameter, which allows for the exclusion of specific intramolecular distances (e.g., bonds within the same molecule) from the calculation, which is vital for obtaining physically meaningful results in molecular systems [7]. The class outputs the RDF (g{ab}(r)) or, if the density parameter is set to True, the single-particle density (n{ab}(r) = \rho g_{ab}(r)) [7].

MDAnalysis InterRDF_s Class: This class specializes in calculating site-specific RDFs. Instead of averaging over two large groups, it takes a list of specific pairs of AtomGroup instances. This is particularly valuable for analyzing the local environment around specific residues in a protein binding site or atoms of a ligand [7]. The output is a list of 2D arrays, providing an individual RDF for each unique atom-atom pair between the specified groups.

GROMACS gmx rdf Tool: This tool is part of the highly optimized GROMACS package. It calculates the RDF by dividing the simulation box into spherical slices (from (r) to (r+dr)) and building a histogram of pairwise distances [9]. A distinctive feature of gmx rdf is its ability to compute an angle-dependent RDF (g_{AB}(r,\theta)), where the angle (\theta) is defined relative to a laboratory-fixed axis. This is essential for analyzing the structure of anisotropic systems, such as lipids in a bilayer membrane or molecules at an interface [9].

Table 2: Quantitative Output and Data Structure Comparison

Package/Class	Primary Output	Output Data Structure	Advanced Outputs
MDAnalysis InterRDF	(g{ab}(r)) or (n{ab}(r))	1D array (average RDF)	Raw count histogram, bin edges
MDAnalysis InterRDF_s	List of site-specific (g_{ab}(r))	List of 2D arrays (shape: len(A), len(B))	Cumulative Distribution Function (CDF) via get_cdf() method
GROMACS gmx rdf	(g_{AB}(r))	1D array (standard), 2D array (angle-dependent)	Xmgr-compatible files, coordination numbers

Experimental Protocol for RDF Calculation and Benchmarking

Workflow for Structural Analysis

The following diagram illustrates the generalized protocol for calculating and benchmarking RDFs, from system preparation to analysis.

Step-by-Step Application Notes

• System Preparation and Trajectory Generation:

  • Begin with a fully equilibrated MD system. The initial structure can be sourced from databases like the Protein Data Bank (PDB) for biomolecules or the Materials Project for crystals [23].
  • Run an MD simulation using a package like GROMACS, NAMD, or OpenMM, ensuring the trajectory is saved at a frequency sufficient to resolve the structural features of interest. Critical Consideration: Verify that the simulation has reached thermodynamic equilibrium before collecting data for RDF analysis. This can be checked by monitoring properties like energy and root-mean-square deviation (RMSD) until they plateau [76].

• Atom Group Selection:

  • Define the groups for the RDF calculation. For example, to study solvation, Group A might be a solute molecule or a specific protein residue, and Group B would be the solvent atoms (e.g., oxygen atoms of water) [7] [23].
  • For site-specific analysis with InterRDF_s, prepare a list of pairs of AtomGroup objects, such as [[s1, s2], [s3, s4]], where s1 and s3 are specific atoms of a ligand, and s2 and s4 are specific atoms of a protein binding site [7].

• Parameter Configuration:

  • nbins: The number of bins determines the resolution of the RDF. A typical value is 75, but this may be increased for higher resolution at the cost of noisier data [7].
  • range: The maximum distance to consider, typically set to half the box length to comply with the minimum image convention (e.g., (0.0, 15.0) Ã…ngströms) [7] [9].
  • exclusion_block (MDAnalysis): Used to exclude bonded atoms or atoms within the same molecule from the pairwise distance calculation. For example, a value of (1, 1) excludes the atom itself and its direct bonded neighbors [7].

• Execution and Analysis:

  • Run the RDF calculation on the production portion of the trajectory.
  • Analyze the resulting (g(r)) curve:
    • Identify peak positions to determine characteristic interatomic distances (e.g., first solvation shell) [23].
    • Calculate coordination numbers by integrating the RDF up to the first minimum [7] [9].
    • For anisotropic systems, utilize the angle-dependent RDF in GROMACS to understand directional preferences [9].

The Scientist's Toolkit: Essential Research Reagents and Software

Table 3: Key Research Reagent Solutions for RDF Analysis

Tool/Resource	Type	Primary Function in RDF Analysis	Source/Provider
MDAnalysis	Python Library	A versatile library for the analysis of MD trajectories, including comprehensive RDF implementations (InterRDF, InterRDF_s).	MDAnalysis Foundation
GROMACS	MD Software Suite	A high-performance MD package with integrated, optimized tools for simulation and analysis, including the gmx rdf command.	GROMACS
Protein Data Bank (PDB)	Database	Provides experimentally determined 3D structures of proteins and nucleic acids, used as starting points for MD simulations.	RCSB PDB
Materials Project	Database	A database of computed crystal structures and properties for inorganic materials, useful for initial simulation structures.	Materials Project
Machine Learning Interatomic Potentials (MLIPs)	Computational Model	Enables highly accurate and efficient MD simulations of complex systems, providing reliable trajectories for RDF analysis.	[23]

Visualization of RDF Analysis Logic

The logical relationship between the RDF result, its interpretation, and the underlying atomic configuration is fundamental. The following diagram outlines this process for a canonical example of liquid water.

This application note has provided a benchmark and detailed protocols for employing different RDF implementation packages within MDAnalysis and GROMACS. The choice between a post-processing Python library like MDAnalysis—which offers flexibility and site-specific analysis—and the highly integrated, performance-optimized gmx rdf tool in GROMACS depends on the specific research question and workflow. By following the standardized experimental protocol outlined herein, researchers can robustly characterize the atomic structure of their systems, from simple liquids to complex biomolecules, thereby validating their MD models and gaining deeper insights into material properties and molecular interactions central to drug development and materials design.

Assessing Sensitivity to Force Field Parameters and Simulation Conditions

Molecular dynamics (MD) simulation has become an indispensable tool for investigating the behavior of molecular systems in fields ranging from drug discovery to materials science [14] [77]. The predictive capability of any MD simulation, however, is fundamentally governed by the accuracy of the underlying molecular mechanics force field—the mathematical function that describes the potential energy of a system as a function of its atomic coordinates [78] [79]. Force fields comprise numerous adjustable parameters that are typically fit to quantum mechanical data and experimental observations [78]. Despite careful parameterization, these force fields remain approximations and their limitations can significantly impact simulation outcomes [78] [80].

Recent advances in uncertainty quantification (UQ) have revealed that among the hundreds of parameters in a typical force field, only a small subset tends to dominate the uncertainty in predicted quantities of interest [80]. This insight, coupled with the fact that molecular dynamics is inherently chaotic and sensitive to initial conditions, necessitates rigorous assessment of parameter sensitivity [80]. The radial distribution function (RDF) serves as a crucial structural metric for such assessments, providing a quantitative measure of atomic organization in materials and biological systems [2] [3]. This application note establishes integrated protocols for evaluating force field parameter sensitivity with RDF analysis as a central validation tool, creating a framework for improving force field reliability in molecular simulations.

Background and Significance

Force Field Parameter Sensitivity in MD Simulations

Classical molecular dynamics simulations approximate atomic interactions using parameterized force fields that include terms for bonded interactions (bonds, angles, dihedrals) and non-bonded interactions (electrostatics, van der Waals) [79]. The sensitivity of simulation outcomes to variations in these parameters has emerged as a critical research focus, particularly as MD applications expand into predictive science and decision-making contexts [80]. Uncertainty quantification studies demonstrate that molecular dynamics manifests both aleatoric uncertainty (inherent randomness from chaotic dynamics) and epistemic uncertainty (from imperfect force field parameters) [80]. The latter can be systematically reduced through improved parameterization strategies informed by sensitivity analysis [78] [80].

Recent high-dimensional UQ studies employing active subspace methods and machine learning techniques have revealed that force fields exhibit "sloppiness"—most parameters have minimal impact on outputs, while a small subset controls the majority of prediction uncertainty [80]. This phenomenon enables significant dimensionality reduction in parameter optimization problems. For instance, global sensitivity analysis of interaction potentials identified that Lennard-Jones parameters and specific dihedral terms frequently dominate uncertainty in key quantities of interest, including binding free energies and material properties [78] [80].

Radial Distribution Functions as Structural Validators

The radial distribution function, g(r), provides a fundamental measure of molecular structure by quantifying the probability of finding particle pairs at specific separation distances compared to an ideal gas [2] [7]. In MD analysis, RDFs serve as essential validation metrics because they:

• Provide atomistic-resolution structural information that can be directly compared against experimental data from X-ray diffraction or neutron scattering [2] [3]
• Are highly sensitive to changes in non-bonded interaction parameters, particularly Lennard-Jones terms and partial atomic charges [80] [3]
• Can be computed with high precision from simulation trajectories, enabling quantitative assessment of force field performance [7]
• Capture the organization of solvation shells around solutes and within binding pockets, critical for modeling molecular recognition [78] [7]

For these reasons, RDF analysis provides an ideal structural benchmark for assessing how variations in force field parameters propagate to changes in simulated system organization.

Table 1: Key Sensitivity Analysis Methods for Force Field Parameters

Method	Key Features	Dimensionality Scope	Implementation Considerations
Local Sensitivity Analysis	Evaluates partial derivatives at fixed parameter values; computationally efficient	Low to moderate	Requires careful selection of baseline parameters; may miss non-linear effects
Global Sensitivity Analysis	Assesses parameter effects across broad value ranges; identifies interactions	High	Computationally demanding; benefits from active subspace dimensionality reduction
Active Subspace Methods	Identifies linear parameter combinations that dominate output variance	High	Enables dramatic dimensionality reduction; incorporates machine learning
Sloppiness Identification	Eigenvalue decomposition of Fisher Information Matrix; identifies stiff/sloppy parameter directions	Moderate to high	Provides local sensitivity landscape around optimal parameters

Integrated Protocol for Sensitivity Assessment

This section presents a comprehensive workflow for evaluating force field parameter sensitivity using RDF-based structural validation. The protocol integrates parameter perturbation, ensemble simulation, and quantitative RDF analysis.

Parameter Selection and Perturbation Strategy

• Parameter Prioritization:

  • Begin by identifying parameters for sensitivity testing based on prior uncertainty quantification studies. Lennard-Jones well depth (ε) and size (σ) parameters for key atom types typically represent high-priority targets due to their direct influence on intermolecular packing [78] [80].
  • Backbone dihedral terms (φ, ψ, φ', ψ') significantly influence secondary structure preferences in biomolecules and should be included in sensitivity analysis [79].
  • For drug discovery applications, prioritize parameters affecting ligand binding site interactions and solvation thermodynamics [78].

• Perturbation Design:

  • For high-priority parameters, define perturbation ranges based on reported parameter uncertainties or standard deviations across different force field variants [80] [79]. Typical ranges span ±10-30% of nominal values.
  • Employ Latin hypercube sampling or Sobol sequences to efficiently explore high-dimensional parameter spaces when testing multiple parameters simultaneously [80].
  • For computational efficiency, leverage active subspace identification to focus perturbations along parameter combinations that dominate output variance [80].

Ensemble Simulation Setup

• System Preparation:

  • Select benchmark systems appropriate for your research context. For drug development applications, host-guest systems (e.g., cucurbituril complexes) provide excellent model systems with well-characterized binding thermodynamics [78].
  • For membrane protein studies, incorporate lipid bilayer systems with validated force field performance [81].
  • Solvate systems using consistent water models (TIP3P, TIP4P, SPC/E) throughout the parameter perturbation series to isolate force field effects [81].

• Simulation Execution:

  • Perform ensemble simulations (typically 3-5 replicas) for each parameter set using different random seeds to account for aleatoric uncertainty [80].
  • For each parameter set, run equilibration followed by production simulations of sufficient duration to converge RDFs and other structural properties. Simulation length should be determined through careful convergence testing [80].
  • Maintain consistent simulation conditions (temperature, pressure, electrostatic treatment) across all perturbations to ensure comparability [81].

RDF Calculation and Analysis Protocol

• RDF Computation:

  • Extract trajectory frames at consistent intervals (e.g., every 10-50 ps) for RDF calculation, ensuring adequate sampling of structural distributions [7].
  • Calculate site-specific RDFs using established packages such as MDAnalysis or LAMMPS tools, focusing on atom pairs most relevant to the system's structural features [7] [3].
  • For binding-related studies, compute RDFs between host and guest atoms, solvent and solute atoms, and confined water molecules within binding pockets [78] [7].

• Quantitative RDF Analysis:

  • Beyond visual comparison, quantify RDF differences using statistical metrics such as:
    • Integrated squared differences between RDF curves
    • Peak position and height variations in solvation shells
    • Coordination numbers from cumulative RDFs [7]
  • For sensitivity ranking, compute elementary effects or Sobol indices that quantify how parameter changes affect RDF metrics [80].
  • Compare RDFs from parameter-perturbed simulations against reference data, which may include:
    • Experimental RDFs from scattering experiments [2]
    • High-level quantum mechanical calculations [79]
    • Consensus RDFs from multiple force fields [81]

Table 2: Key RDF Metrics for Sensitivity Assessment

RDF Metric	Structural Significance	Parameter Sensitivity
First Peak Position	Equilibrium distance of closest approach	Highly sensitive to Lennard-Jones σ parameters
First Peak Height	Strength of preferential coordination	Sensitive to Lennard-Jones ε and electrostatic parameters
First Minimum Depth	Definition of first solvation shell	Indicates sharpness of solvation boundary
Coordination Number	Number of atoms in first solvation shell	Integrative measure of local packing
Second Shell Structure	Medium-range ordering	Sensitive to combined non-bonded parameter effects

Application Notes for Specific Research Contexts

Drug Discovery: Protein-Ligand Binding

In pharmaceutical applications, accurately predicting protein-ligand binding thermodynamics remains a fundamental challenge. Current force fields show systematic deviations in binding enthalpy calculations, with errors of 3.0-6.8 kcal/mol observed in host-guest systems [78]. To address this:

• Implement sensitivity analysis on Lennard-Jones parameters for key functional groups involved in binding interactions [78].
• Compute RDFs between protein binding site atoms and ligand atoms across parameter variations.
• Focus particularly on RDFs involving hydrophobic binding pockets and polar interaction sites, as these exhibit distinct parameter sensitivities [78].
• Use host-guest systems as computationally efficient proxies for protein-ligand systems when performing initial parameter sensitivity screening [78].

Biomolecular Force Fields: Protein Secondary Structure

Accurate modeling of protein secondary structure represents a longstanding challenge in force field development. Early force fields (ff94, ff99) exhibited systematic biases, overstabilizing α-helical structures [79]. Assessment protocols should include:

• Sensitivity testing of backbone dihedral parameters (φ, ψ) and their coupling terms (φ', ψ') [79].
• RDF analysis between backbone atoms and solvent molecules to assess hydration of secondary structural elements.
• Comparison of RDF-derived solvation patterns around α-helices versus β-sheets across parameter variations.
• Integration with NMR-derived structural parameters to validate force field performance against experimental data [79].

Materials Science: Liquid Membranes and Ether Systems

For materials applications such as liquid ion-selective membranes, accurately modeling transport and interfacial properties is essential [81]. Force field assessment should focus on:

• Sensitivity of RDFs between ether oxygen atoms and alkali metal ions to Lennard-Jones and charge parameters [81].
• Comparison of RDF-derived solvation structures against experimental scattering data.
• Assessment of density and viscosity predictions across parameter variations, as these properties directly impact membrane performance [81].
• Recent studies indicate CHARMM36 outperforms GAFF and OPLS-AA for ether-based systems, particularly for viscosity predictions where GAFF and OPLS-AA show 60-130% errors [81].

The Scientist's Toolkit: Essential Research Reagents

Table 3: Essential Computational Tools for Sensitivity Analysis

Tool/Category	Specific Examples	Function in Analysis	Implementation Notes
MD Simulation Packages	AMBER, GROMACS, LAMMPS, NAMD	Core simulation engine	Select packages with robust parameter modification capabilities
RDF Analysis Tools	MDAnalysis, TRAVIS, VMD, LAMMPS RDF	Calculate radial distribution functions	MDAnalysis provides InterRDF for site-specific analysis [7]
Sensitivity Analysis Frameworks	Active Subspace Toolbox, SALib, Custom Python	Parameter screening and sensitivity quantification	Implement active subspace methods for high-dimensional problems [80]
Force Fields	AMBER/GAFF, CHARMM, OPLS-AA, COMPASS	Provide baseline parameters	CHARMM36 recommended for ether systems [81]
Uncertainty Quantification Tools	UQ Toolkit (Sandia), Chaospy, Monte Carlo	Quantify epistemic and aleatoric uncertainty	Essential for rigorous sensitivity assessment [80]
Visualization Software	VMD, PyMOL, Matplotlib, Seaborn	Visualize RDFs and parameter relationships	Critical for interpreting complex sensitivity relationships

Advanced Methodologies and Emerging Approaches

High-Dimensional Uncertainty Quantification

Traditional sensitivity analysis methods struggle with the high dimensionality of modern force fields, which may contain hundreds of adjustable parameters. Emerging approaches address this challenge through:

• Active Subspace Methods: These identify low-dimensional linear combinations of parameters that dominate output variance. The active subspace is determined through eigenvalue decomposition of a global matrix constructed from the gradient of model outputs with respect to parameters [80].
• Gaussian Process Regression: When combined with active subspaces, this machine learning technique creates efficient surrogate models that map force field parameters to simulation outputs, dramatically reducing computational costs for sensitivity analysis [80].
• Sloppiness Characterization: By analyzing the eigenvalue spectrum of the Fisher Information Matrix, researchers can identify "stiff" parameter directions (strongly constrained by data) and "sloppy" directions (poorly constrained), focusing sensitivity analysis on the most influential parameter combinations [80].

Enhanced Sampling for Binding Thermodynamics

Accurately quantifying the sensitivity of binding free energies and enthalpies to force field parameters requires enhanced sampling approaches:

• Attach-Pull-Release (APR) Methods: These compute potentials of mean force along binding pathways, providing numerically precise free energy estimates for parameter sensitivity assessment [78].
• Hamiltonian Replica Exchange: This approach enhances sampling efficiency when evaluating parameter perturbations, particularly for protein-ligand systems [78].
• Alchemical Free Energy Methods: When combined with parameter sensitivity analysis, these provide rigorous assessment of how force field parameters influence binding affinity predictions [78].

Machine Learning-Enhanced Force Field Optimization

Machine learning approaches are transforming force field development and sensitivity analysis:

• Neural Network Potentials: These can learn complex relationships between atomic configurations and energies, providing reference data for traditional force field sensitivity assessment [80].
• Gradient-Enhanced Sensitivity Analysis: By computing derivatives of simulation outputs with respect to parameters, researchers can efficiently map the local sensitivity landscape and identify optimal parameter adjustment directions [78] [80].
• Transfer Learning: Sensitivity patterns identified in simple model systems (e.g., host-guest complexes) can inform parameter optimization for more complex biomolecular systems, accelerating force field improvement [78].

Systematic assessment of force field parameter sensitivity, with RDF analysis as a central validation tool, represents a crucial methodology for advancing the predictive capability of molecular dynamics simulations. The integrated protocols presented in this application note provide researchers with a structured approach to identify parameters that dominate uncertainty in simulation outcomes. By implementing these sensitivity analysis frameworks across diverse research contexts—from drug discovery to materials science—researchers can prioritize force field improvements for maximum impact. The emerging methodologies in high-dimensional uncertainty quantification and machine learning promise to further enhance our ability to refine force fields systematically, ultimately increasing the reliability of molecular simulations in scientific and decision-making contexts.

Conclusion

The Radial Distribution Function serves as a powerful bridge connecting MD simulations with tangible atomic-level structural insights, proving indispensable for modern biomedical research. By mastering RDF fundamentals, implementation methods, optimization strategies, and validation techniques, researchers can reliably extract crucial information about molecular interactions, solvation structures, and dynamic processes in biological systems. The integration of RDF analysis with other computational and experimental approaches provides a robust framework for understanding complex biomolecular phenomena, particularly in drug design targeting proteins like EGFR and H-Ras. Future directions include developing more efficient RDF algorithms for massive simulation datasets, enhancing machine learning integration for pattern recognition, and establishing standardized protocols for clinical translation of RDF-derived insights in personalized medicine and targeted therapy development.

References

• 1. A review on the radial distribution function: Insights into ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732225010773]
• 2. Radial distribution function [https://en.wikipedia.org/wiki/Radial_distribution_function]
• 3. Radial Distribution Function (RDF) [https://lammpstube.com/2023/11/05/radial-distribution-function-rdf/]
• 4. Fast Analysis of Molecular Dynamics Trajectories with ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3085256/]
• 5. 4.8.2.1. Radial Distribution Functions [https://docs.mdanalysis.org/stable/documentation_pages/analysis/rdf.html]
• 6. 4.7.2.1. Radial Distribution Functions [https://docs.mdanalysis.org/2.0.0/documentation_pages/analysis/rdf.html]
• 7. 4.7.3. Radial Distribution Functions [https://docs.mdanalysis.org/1.1.1/documentation_pages/analysis/rdf.html]
• 8. Radial Distribution Function - an overview [https://www.sciencedirect.com/topics/chemistry/radial-distribution-function]
• 9. Radial distribution functions [https://manual.gromacs.org/current/reference-manual/analysis/radial-distribution-function.html]
• 10. A connection between the density and temperature of ... [https://www.sciencedirect.com/science/article/abs/pii/S0378381222003284]
• 11. 4.7.2.1. Radial Distribution Functions [https://docs.mdanalysis.org/2.1.0/documentation_pages/analysis/rdf.html]
• 12. Testing of the GROMOS Force-Field Parameter Set 54A8 [https://pmc.ncbi.nlm.nih.gov/articles/PMC3572754/]
• 13. 1.2: Radial Distribution Function [https://chem.libretexts.org/Bookshelves/Biological_Chemistry/Concepts_in_Biophysical_Chemistry_(Tokmakoff)/01%3A_Water_and_Aqueous_Solutions/01%3A_Fluids/1.02%3A_Radial_Distribution_Function]
• 14. Molecular dynamics simulation for all - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC6209097/]
• 15. Mastering Molecular in Computational Chemistry Dynamics [https://www.numberanalytics.com/blog/mastering-molecular-dynamics-computational-chemistry]
• 16. Best Practices for Foundations in Molecular Simulations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6884151/]
• 17. Prediction of thermophysical properties of R-454B based on... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12141669/]
• 18. Protocol for Molecular Dynamics Simulations of Proteins [https://en.bio-protocol.org/en/bpdetail?id=2051&type=0]
• 19. Radial Distribution Function - (Physical Chemistry I) [https://fiveable.me/key-terms/physical-chemistry-i/radial-distribution-function]
• 20. Radial Distribution Function - an overview [https://www.sciencedirect.com/topics/mathematics/radial-distribution-function]
• 21. Liquid–A dynamic mixture of gas-like and solid-like states [https://www.sciencedirect.com/science/article/abs/pii/S0301010425001260]
• 22. and Radial network graphs of... distribution hydrogen bonded [https://pubmed.ncbi.nlm.nih.gov/37084111/]
• 23. Molecular Dynamics Simulations for Materials and ... [https://matlantis.com/en/resources/blog/md-intro/]
• 24. Introduction — MD DaVis 0.4.1 documentation [https://md-davis.readthedocs.io/en/latest/introduction.html]
• 25. Tools for structural analysis on LAMMPS trajectories [https://mattermodeling.stackexchange.com/questions/2122/tools-for-structural-analysis-on-lammps-trajectories]
• 26. compute rdf command [https://docs.lammps.org/compute_rdf.html]
• 27. Trajectory Analysis — AMS 2025.1 documentation - SCM [https://www.scm.com/doc/AMS/Utilities/TrajectoryAnalysis.html]
• 28. Exercise: Molecular Dynamics Analysis [https://agkeller.userpage.fu-berlin.de/source/exercises_b/eb_md_analysis.html]
• 29. Targeted Molecular Dynamics [https://www.charmm-gui.org/charmmdoc/tmd.html]
• 30. Molecular Dynamics Simulations in Drug Discovery and ... [https://www.mdpi.com/2227-9717/9/1/71]
• 31. 3. Selection commands — MDAnalysis 2.9.0 documentation [https://docs.mdanalysis.org/2.9.0/documentation_pages/selections.html]
• 32. Atom Selection Reference — MDTraj 1.9.4 documentation [https://mdtraj.org/1.9.4/atom_selection.html]
• 33. Periodic Boundary Conditions - an overview | ScienceDirect Topics [https://www.sciencedirect.com/topics/biochemistry-genetics-and-molecular-biology/periodic-boundary-conditions]
• 34. Periodic boundary conditions [https://en.wikipedia.org/wiki/Periodic_boundary_conditions]
• 35. Do "minimum image convention" and "nearest image" talks ... [https://mattermodeling.stackexchange.com/questions/11078/do-minimum-image-convention-and-nearest-image-talks-about-the-same-things]
• 36. Periodic Boundary Conditions [https://www.uoxray.uoregon.edu/local/manuals/biosym/discovery/General/Describe_Sys/PB_Cond.html]
• 37. Molecular Dynamics: Periodic Boundary Conditions (PBC) [https://www.compchems.com/molecular-dynamics-periodic-boundary-conditions-pbc/]
• 38. Molecular Simulation/Periodic Boundary Conditions - Wikibooks, open books for an open world [https://en.wikibooks.org/wiki/Molecular_Simulation/Periodic_Boundary_Conditions]
• 39. Periodic boundary conditions [https://manual.gromacs.org/2021-rc1/reference-manual/algorithms/periodic-boundary-conditions.html]
• 40. Minimum image convention for non-orthorhombic unit cells [https://mattermodeling.stackexchange.com/questions/4618/minimum-image-convention-for-non-orthorhombic-unit-cells]
• 41. Molecular Dynamics Simulation [https://www.cgl.ucsf.edu/chimera/current/docs/ContributedSoftware/md/md.html]
• 42. Running Molecular Dynamics on Alliance clusters with AMBER [https://computecanada.github.io/molmodsim-amber-md-lesson/design/]
• 43. Modelling ligand exchange in metal complexes with machine ... [https://pubs.rsc.org/en/content/articlehtml/2025/fd/d4fd00140k]
• 44. Hydration structure of salt solutions from ab initio molecular ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8487239/]
• 45. On the structure of hybrid water-in-salt electrolytes [https://pubs.rsc.org/en/content/articlehtml/2025/cp/d5cp00680e]
• 46. Title: Identification of Redox State Based on the Difference ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12075091/]
• 47. Non-local X-ray intermolecular radiative decay probes ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12623427/]
• 48. Activation of the EGF Receptor by Ligand Binding and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5492017/]
• 49. Conformational diversity and protein–protein interfaces in ... [https://www.nature.com/articles/s41598-023-50913-8]
• 50. Allosteric Regulation at the Crossroads of New Technologies [https://www.frontiersin.org/journals/molecular-biosciences/articles/10.3389/fmolb.2020.00136/full]
• 51. Allo-network drugs: harnessing allostery in cellular networks [https://pmc.ncbi.nlm.nih.gov/articles/PMC7380718/]
• 52. Dynamic allosteric networks drive adenosine A1 receptor ... [https://elifesciences.org/articles/90773]
• 53. Toward the Design of Allosteric Effectors [https://pmc.ncbi.nlm.nih.gov/articles/PMC11472305/]
• 54. 4.8.1. Generating densities from trajectories [https://docs.mdanalysis.org/1.0.0/documentation_pages/analysis/density.html]
• 55. 4.8.1. Generating densities from trajectories [https://docs.mdanalysis.org/2.5.0/documentation_pages/analysis/density.html]
• 56. Machine learning analysis of molecular dynamics ... [https://www.nature.com/articles/s41598-025-11392-1]
• 57. Radial distribution function fitting [https://bio-protocol.org/exchange/minidetail?id=4496761&type=30]
• 58. Advancing drug development with “Fit-for-Purpose” modeling ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12436579/]
• 59. GPU Accelerated Hybrid Particle‐Field Molecular Dynamics [https://pmc.ncbi.nlm.nih.gov/articles/PMC12076535/]
• 60. Calculating the RDF atom-to-atom [https://userguide.mdanalysis.org/1.1.1/examples/analysis/structure/site_specific_rdf.html]
• 61. Color shift when GPU acceleration is ON in lightro... [https://community.adobe.com/t5/lightroom-classic-discussions/color-shift-when-gpu-acceleration-is-on-in-lightroom-develop-mode-windows-system/td-p/14405099]
• 62. Radial distribution functions [https://manual.gromacs.org/documentation/2025.1/reference-manual/analysis/radial-distribution-function.html]
• 63. Ultimate sensitivity of radial distribution functions to ... [https://www.sciencedirect.com/science/article/abs/pii/S0927025622001148]
• 64. Evaluation of uncertainties in atomic data on spectral lines ... [https://link.springer.com/article/10.1140/epjd/s10053-024-00820-y]
• 65. Using the Radial Distribution Function to Analyze Atomic ... [https://www.mdpi.com/1422-0067/26/1/210]
• 66. Model-free estimation of completeness, uncertainties, and ... [https://www.nature.com/articles/s41467-025-59232-0]
• 67. Hierarchical Model for the Analysis of Scattering Data ... [https://link.springer.com/article/10.1007/s11837-016-1928-8]
• 68. Experimental Approaches for Solution X-Ray Scattering and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2659704/]
• 69. X-ray scattering techniques [https://en.wikipedia.org/wiki/X-ray_scattering_techniques]
• 70. Introduction to X-ray Scattering [https://www.teledynevisionsolutions.com/learn/learning-center/scientific-imaging/introduction-to-x-ray-scattering/]
• 71. Neutron scattering [https://en.wikipedia.org/wiki/Neutron_scattering]
• 72. Eliminating finite-size effects on the calculation of x-ray ... [https://pubmed.ncbi.nlm.nih.gov/38127395/]
• 73. ADMET profiling, molecular docking, dynamics, PCA, and end ... [https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0327862]
• 74. ADMET profiling, molecular docking, dynamics, PCA, and end ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12240381/]
• 75. Uncovering the Mechanism of Drug Resistance Caused ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9189374/]
• 76. Convergence and equilibrium in molecular dynamics ... [https://www.nature.com/articles/s42004-024-01114-5]
• 77. Molecular dynamics [https://en.wikipedia.org/wiki/Molecular_dynamics]
• 78. Toward Improved Force-Field Accuracy through Sensitivity ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4664157/]
• 79. Comparison of multiple AMBER force fields and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4805110/]
• 80. Global ranking of the sensitivity of interaction potential ... [https://www.nature.com/articles/s41524-024-01272-z]
• 81. Force field comparison for molecular dynamics simulations ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732224024061]