Configurational Entropy in Intermolecular Interactions: From Theory to Application in Drug Design

Abstract

This article provides a comprehensive analysis of the critical role configurational entropy plays in governing intermolecular interactions, with a specific focus on biomedical and pharmaceutical applications. It explores the fundamental thermodynamic principles that define configurational entropy and its relationship to binding free energy. The scope extends to contemporary computational and experimental methodologies for its quantification, strategies to overcome ubiquitous challenges such as enthalpy-entropy compensation, and validation through case studies in successful drug optimization. Tailored for researchers, scientists, and drug development professionals, this review synthesizes foundational knowledge with cutting-edge applications to guide the rational design of high-affinity molecular binders.

The Thermodynamic Pillar: Defining Configurational Entropy and Its Role in Binding Free Energy

This technical guide explores the fundamental roles of enthalpy and entropy in driving molecular interactions, with a specific focus on the critical contribution of configurational entropy in biomolecular binding processes. For researchers in drug development, understanding this delicate balance is paramount for overcoming challenges such as enthalpy-entropy compensation and for designing high-affinity therapeutic compounds. This whitepaper synthesizes current research findings, presents quantitative data on entropy changes, details experimental methodologies for its measurement, and provides visual tools for conceptualizing these complex thermodynamic relationships.

Core Thermodynamic Principles

The Gibbs free energy change (ΔG) dictates the spontaneity of molecular binding events and is described by the fundamental equation:

ΔG = ΔH - TΔS

Where ΔH is the change in enthalpy, T is the absolute temperature, and ΔS is the change in the total entropy of the system. A negative ΔG indicates a favorable reaction. The total entropy change (ΔS_system) comprises both solvent entropy and the configurational entropy of the solute molecules themselves [1]. Configurational entropy is the portion of a system's entropy related to the number of discrete representative positions or conformations its constituent particles can adopt [2].

For a system, the configurational entropy can be calculated using the Gibbs entropy formula: S = -kB * Σ(Pn * ln Pn) where kB is the Boltzmann constant and P_n is the probability of the system being in state n out of W possible states [2].

The Critical Role of Configurational Entropy in Biomolecular Binding

Traditionally, the driving force for non-covalent binding was attributed predominantly to favorable enthalpy changes (ΔH) and solvent entropy gains. However, recent experimental and computational studies demonstrate that the loss of configurational entropy upon binding is a major and often unfavorable term that must be overcome [1] [3].

When a receptor and ligand bind, their motions become restricted, leading to a significant loss of configurational entropy. This entropy penalty can be of similar magnitude to the solvent entropy contribution and thus critically influences the overall binding affinity [1]. For example, in protein-ligand binding, this entropy loss can contribute a free energy penalty on the order of 14 kcal mol⁻¹, a substantial value on the scale of typical binding free energies [3]. The table below summarizes key quantitative findings from recent research.

Table 1: Quantified Configurational Entropy Changes in Protein Interactions

Protein/Complex System	Key Finding on Configurational Entropy	Magnitude / Impact
General Protein Binding	Total configurational entropy change (ΔS_conf) is a central constituent of the free energy change (ΔG) [1].	Similar magnitude to solvent entropy contribution [1].
Tsg101 / PTAP Peptide Binding	First-order MIE approximation of entropy change (neglecting correlations) [3].	Free energy penalty of 14 kcal mol⁻¹ (12 from protein, 2 from ligand) [3].
Ubiquitin Complexes (e.g., 1S1Q, 1YD8)	Unfavorable entropy change from internal degrees of freedom without coupling terms (-TΔS_1D) [1].	Ranges from 44.0 to 527.4 kJ mol⁻¹ per partner, showing system-dependent variability [1].
Protein-Ligand Binding	Change in pairwise correlation is a major contributor to the total computed change in configurational entropy [3].	Major contribution to overall entropy loss [3].

Decomposing Configurational Entropy: Insights from Mutual Information Expansion

The Mutual Information Expansion (MIE) provides a powerful, systematic framework for dissecting the total configurational entropy into contributions from individual molecular degrees of freedom and their correlations [3]. The second-order MIE approximation is given by:

S ≈ S^(2) = Σ Si - Σ Iij

where Si is the entropy of the i-th degree of freedom, and Iij is the mutual information between coordinates i and j, which accounts for both linear and nonlinear correlations [3].

Applying this analytical framework reveals that contrary to traditional assumptions, coupling terms between internal and external degrees of freedom contribute significantly to the overall configurational entropy change upon binding [1]. This decomposition is vital for a precise understanding of binding thermodynamics.

Experimental and Computational Protocols

Molecular Dynamics (MD) with MIE/MIST Analysis

This protocol is used to calculate configurational entropy changes from atomistic simulations [1] [3].

• System Preparation: Construct the all-atom model of the free binding partners and their bound complex using a molecular modeling suite. Solvate the systems in an explicit water box and add ions to neutralize the charge.
• Equilibration: Run a series of MD simulations, first relaxing the solvent and ions, then the entire system, under NPT (constant Number of particles, Pressure, and Temperature) conditions to achieve stable temperature, density, and potential energy.
• Production Simulation: Perform microsecond-long MD simulations for each state (free and bound) to ensure adequate sampling of conformational space. Multiple independent replicates (MMDS) are recommended to improve statistical reliability [3].
• Trajectory Analysis in BAT Coordinates: Convert the Cartesian coordinates from the MD trajectories into internal Bond-Angle-Torsion (BAT) coordinates.
• Entropy Calculation: Apply the Maximum Information Spanning Tree (MIST) algorithm or the second-order MIE approximation to the BAT coordinate trajectories. This yields the total configurational entropy and its decomposition into uncoupled and coupling terms for each state [1].
• Calculate Change: The configurational entropy change of binding (ΔS_conf) is the difference between the entropy of the complex and the sum of the entropies of the isolated partners.

NMR Spectroscopy-Based Estimation

This method uses experimental data to estimate changes in molecular flexibility.

• Sample Preparation: Prepare isotopically labeled samples of the free protein and the protein-ligand complex.
• NMR Data Collection: Conduct NMR relaxation experiments (e.g., measuring T1, T2, and NOE) to determine generalized order parameters (S²) for backbone N-H bond vectors.
• Entropy Estimation: Relate the order parameters to conformational entropy using a model, such as the "diffusion-in-a-cone" model. The entropy is inversely related to the order parameter (higher S² indicates less motion and lower entropy) [3].
• Limitation: This approach typically provides an estimate based on internal degrees of freedom only and may not account for all correlation effects [1] [3].

Table 2: Key Research Reagent Solutions for Configurational Entropy Studies

Item / Resource	Function / Application
Molecular Dynamics Software (e.g., GROMACS, AMBER, NAMD)	Performs all-atom simulations to generate conformational ensembles of molecules and complexes.
MIE/MIST Analysis Code (e.g., custom parallel implementations)	Computes configurational entropy and its components from MD simulation trajectories [1].
Isotopically Labeled Proteins (¹⁵N, ¹³C)	Essential for NMR relaxation experiments to measure dynamics and order parameters.
High-Performance Computing (HPC) Cluster	Provides the computational power required for microsecond-scale MD simulations and subsequent entropy analysis.
Force Fields (e.g., CHARMM, AMBER)	Defines the potential energy functions and parameters governing interatomic interactions in MD simulations.

Implications for Drug Discovery and Development

The insights from configurational entropy research directly impact rational drug design.

• Overcoming Enthalpy-Entropy Compensation: This common phenomenon, where optimizing favorable enthalpy leads to a compensating loss of entropy (or vice versa), is a major hurdle. A detailed understanding of entropy contributions can guide strategies to mitigate this effect [1].
• Identifying "Entropy Hotspots": MIE analysis can pinpoint specific molecular degrees of freedom (e.g., key torsional angles) that lose the most entropy upon binding. This information can be used to design ligands that pre-organize into the bioactive conformation, reducing the entropic penalty paid upon binding.
• Stabilizing Specific Protein Dynamics: In some cases, a ligand might increase the flexibility (and thus entropy) of the receptor in specific modes, which can be a mechanism for high-affinity binding [3]. Targeting such dynamics is a sophisticated design strategy.
• Amorphous Pharmaceutical Formulations: The high configurational entropy of amorphous drugs compared to their crystalline counterparts is a key factor in their enhanced solubility. However, this same property provides the thermodynamic driving force for recrystallization, which is a primary stability challenge. Understanding this balance is critical for formulating stable amorphous solid dispersions [4].

Configurational entropy is a fundamental thermodynamic property originating from the disorder inherent in the spatial and energetic degrees of freedom of molecules. In biomolecular interactions, particularly noncovalent binding events, the change in configurational entropy constitutes a central component of the free energy change, profoundly influencing binding affinity and specificity. Despite its significance, configurational entropy remains challenging to quantify experimentally or computationally. This whitepaper provides an in-depth examination of configurational entropy's theoretical foundations, presents advanced computational methodologies for its dissection, and discusses its critical implications for rational drug design, where overcoming enthalpy-entropy compensation is a pivotal challenge.

Configurational entropy is the component of total entropy that arises specifically from the number of distinct spatial arrangements accessible to a molecule's atoms, excluding contributions from solvent molecules [1]. In the context of noncovalent interactions between biomacromolecules—processes fundamental to transcription, translation, and cell signaling—the change in configurational entropy (ΔS_conf) upon binding represents a substantial contribution to the overall Gibbs free energy change (ΔG) [1].

Traditional assumptions held that configurational entropy change was negligible compared to solvent entropy changes in biomolecular interactions. However, experimental evidence now demonstrates that configurational entropy contributions in proteins can be of similar magnitude to solvent entropy contributions, potentially exerting a strong influence on interaction thermodynamics [1]. This recognition has significant applied implications, as deeper insight into configurational entropy and the physical principles governing its response to biomolecular dynamics could substantially improve computational drug design by helping to overcome persistent enthalpy/entropy compensation effects [1].

The theoretical framework for configurational entropy derives from the quasi-classical entropy integral. For a single molecule or complex, configurational entropy can be expressed as [1]: $$S_{config} = -R \int \rho(\vec{q}) \ln [h^{3N} J(\vec{q}) \rho(\vec{q})] d\vec{q} + R \ln (8\pi^2 V^\circ)$$ Where R is the universal gas constant, h is Planck's constant, N is the number of atoms, ρ is the classical phase-space probability density function, $\vec{q}$ represents spatial degrees of freedom, J($\vec{q}$) denotes the Jacobian of the chosen internal coordinates, and V° is the standard concentration volume.

Theoretical Framework and Decomposition

Molecular Degrees of Freedom

The configurational entropy of a biomolecule can be conceptually and mathematically decomposed into contributions from different classes of molecular degrees of freedom:

• Internal degrees of freedom: These include bond stretching, angle bending, and torsional rotations, typically described in Bond-Angle-Torsion (BAT) coordinates or anchored Cartesian coordinates [1].
• External (rigid body) degrees of freedom: These comprise rotational and translational motions of the molecule as a whole [1].
• Coupling terms: These account for correlations and mutual information between internal and external degrees of freedom [1].

A comprehensive framework for this decomposition employs Mutual Information Expansion (MIE) in its analytical form, which enables dissection of the configurational entropy change of binding into contributions from molecular internal and external degrees of freedom while accounting for all coupled and uncoupled contributions [1].

Entropy Decomposition Framework

The following diagram illustrates the analytical framework for decomposing configurational entropy into its constituent components, accounting for couplings between different degrees of freedom:

Contrary to commonly accepted assumptions, different coupling terms contribute significantly to the overall configurational entropy change in protein binding processes [1]. While the magnitude of individual terms may be largely unpredictable a priori, the total configurational entropy change can often be approximated by rescaling the sum of uncoupled contributions from internal degrees of freedom only, providing theoretical support for NMR-based approaches to configurational entropy change estimation [1].

Computational Methodologies and Protocols

Maximum Information Spanning Tree (MIST) Algorithm

The Maximum Information Spanning Tree (MIST) algorithm represents a sophisticated approach for configurational entropy calculation from molecular dynamics simulations [1]. This method, which can be considered a variant of Mutual Information Expansion (MIE), enables efficient approximation of the high-dimensional integrals required for entropy computation.

Protocol Implementation:

• Trajectory Generation: Perform microsecond-level classical molecular dynamics simulations of both isolated binding partners and their binary complexes [1].
• Coordinate Transformation: Convert Cartesian coordinates to internal coordinates (typically BAT coordinates) to separate internal and external degrees of freedom [1].
• Probability Density Estimation: Compute marginal and joint probability distributions for all degrees of freedom from simulation trajectories.
• Mutual Information Calculation: Determine mutual information between all pairs of degrees of freedom.
• Spanning Tree Construction: Build the maximum information spanning tree that connects all degrees of freedom while maximizing total mutual information.
• Entropy Computation: Calculate configurational entropy using the MIST approximation, which decomposes the total entropy into individual and pairwise correlated contributions.

Recent parallel implementations of the MIST algorithm have enabled comprehensive numerical analysis of individual contributions to configurational entropy change across extensive sets of protein binding processes [1].

Dynamic Disorder in Molecular Crystals

Beyond biomolecules in solution, computational approaches also address dynamic disorder in molecular crystals, where molecular segments or entire molecules exhibit large-amplitude motions [5]. These methods sample potential energy surfaces to model atomic displacements related to disorder and quantify contributions of internal dynamics to macroscopic material properties.

Computational Workflow for Dynamic Disorder Analysis:

• Potential Energy Surface Mapping: Identify flat potential energy basins related to dynamic degrees of freedom using quantum chemical calculations [5].
• Anharmonicity Assessment: Evaluate the extent of anharmonicity in dynamic degrees of freedom through potential energy profile analysis along libration modes [5].
• Thermodynamic Integration: Incorporate anharmonic models (e.g., hindered rotor models) into quasi-harmonic treatment of thermodynamic properties [5].
• Property Prediction: Calculate contributions of dynamic disorder to entropy, volatility, solubility, and other material properties [5].

For caged molecules with rotational disorder, such as adamantane and diamantane derivatives, this approach has revealed significant additional entropy contributions due to dynamic disorder originating from phonon anharmonicity [5].

Quantitative Analysis of Configurational Entropy

Protein Binding Entropy Changes

Computational studies on extensive sets of protein complexes have quantified the magnitude of configurational entropy changes and their components in biological binding processes. The table below summarizes representative data from molecular dynamics simulations of protein binding processes, highlighting the significant variation in entropy contributions across different systems:

Table 1: Configurational Entropy Changes in Protein Binding Processes

Protein System	PDB Code	Uncoupled Internal Entropy Change (-TΔS_1D)	Total Atoms in Complex	Key Findings
Tsg101/Ubiquitin	1S1Q	190.0 kJ/mol (Tsg101)	2,240	Different coupling terms contribute significantly to total entropy change
gGGA3 Gat/Ubiquitin	1YD8	44.0 kJ/mol (gGGA3)	1,709	Magnitude of individual terms largely unpredictable a priori
Subtilisin/Ovomucoid	1R0R	527.4 kJ/mol (Subtilisin)	2,931	Total entropy change approximatable by rescaling uncoupled internal contributions
Uracil-DNA Glycosylase/Inhibitor	1UGH	-65.7 kJ/mol (Glycosylase)	3,121	Supports NMR-based entropy estimation approaches

The data reveal several important patterns. First, the magnitude of uncoupled internal entropy changes varies substantially across different protein systems, ranging from strongly favorable to slightly unfavorable contributions. Second, the data demonstrate that different coupling terms contribute significantly to the overall configurational entropy change, contrary to commonly accepted assumptions in the field. Finally, despite the complexity of these contributions, the total configurational entropy change can often be approximated by rescaling the sum of uncoupled contributions from internal degrees of freedom, providing support for experimental NMR-based approaches to configurational entropy estimation [1].

Dynamic Disorder Entropy Contributions

In molecular crystals, computational studies have quantified the entropy contributions from dynamic disorder, particularly in systems exhibiting rotational freedom or large-amplitude motions:

Table 2: Entropy Contributions from Dynamic Disorder in Molecular Crystals

Material Class	Representative Compound	Energy Barrier for Rotation	Entropy Contribution from Dynamic Disorder	Experimental Manifestation
Caged Hydrocarbons	Diamantane	4-8 kJ/mol	Significant additional contributions beyond harmonic model	Plastic crystal behavior, barocaloric effects
Pharmaceutical Compounds	Various APIs	System-dependent	Affects solubility, stability, and polymorphism	Altered dissolution rates, phase transformations
Organic Semiconductors	Various OSCs	System-dependent	Influences charge carrier mobility	Temperature-dependent conductivity

For diamantane, calculations show rotational energy barriers of 4-8 kJ/mol, which are comparable to thermal energy at ambient conditions (≈2.5 kJ/mol), justifying the need for explicitly anharmonic models. The additional entropy contributions from dynamic disorder in such systems significantly impact material properties including volatility, solubility, and charge transport characteristics [5].

Research Reagent Solutions Toolkit

The computational analysis of configurational entropy requires specialized software tools and theoretical frameworks. The following table details essential "research reagents" for investigating configurational entropy in molecular systems:

Table 3: Essential Computational Tools for Configurational Entropy Research

Tool/Algorithm	Type	Primary Function	Key Applications
Maximum Information Spanning Tree (MIST)	Algorithm	Approximates configurational entropy from molecular dynamics trajectories	Protein binding entropy changes, allosteric regulation studies
Mutual Information Expansion (MIE)	Theoretical Framework	Decomposes entropy into correlated and uncoupled contributions	Entropy component analysis, coupling term quantification
Molecular Dynamics Simulations	Computational Method	Generates conformational ensembles for entropy calculation	Biomolecular dynamics, binding free energy calculations
Hindered Rotor Model	Theoretical Model	Treats anharmonic rotational degrees of freedom	Dynamic disorder in molecular crystals, plastic crystal behavior
Bond-Angle-Torsion (BAT) Coordinates	Coordinate System	Separates internal and external degrees of freedom	Entropy decomposition, internal coordinate analysis
YM-344031	YM-344031, MF:C29H31FN4O3, MW:502.6 g/mol	Chemical Reagent	Bench Chemicals
Aminohexylgeldanamycin hydrochloride	Aminohexylgeldanamycin hydrochloride, MF:C34H53ClN4O8, MW:681.3 g/mol	Chemical Reagent	Bench Chemicals

These computational tools enable researchers to move beyond simplistic harmonic approximations and address the complex, anharmonic nature of molecular motions that contribute to configurational entropy in both biomolecular systems and molecular materials.

Implications for Intermolecular Interactions Research

Drug Design and Discovery

In rational drug design, accurate accounting of configurational entropy changes upon binding is crucial for predicting binding affinities and optimizing lead compounds. The recognition that configurational entropy can be similar in magnitude to solvent entropy contributions necessitates more sophisticated computational approaches that properly account for entropy changes in both binding partners [1].

The decomposition of configurational entropy into internal, external, and coupling components provides insights for structure-based drug design. For instance, strategies that restrict flexible moieties in drug candidates may reduce unfavorable entropy losses upon binding, while targeting rigid regions of protein binding sites may minimize entropy penalties.

Material Science Applications

Beyond biomolecular interactions, understanding and controlling configurational entropy has important implications for material design:

• Barocaloric materials: Caged molecules with rotational disorder exhibit significant entropy changes under pressure, enabling solid-state cooling applications [5].
• Pharmaceutical solids: Dynamic disorder in active pharmaceutical ingredients affects solubility, stability, and bioavailability, with metastable disordered forms often exhibiting enhanced dissolution rates [5].
• Organic semiconductors: Configurational entropy influences charge transport properties through its effect on molecular dynamics and disorder in the solid state [5].

Configurational entropy, originating from the disorder in molecular degrees of freedom, represents a fundamental thermodynamic property with far-reaching implications across biochemistry, drug discovery, and materials science. Advanced computational frameworks that decompose configurational entropy into internal, external, and coupling components provide crucial insights into the molecular determinants of entropy changes in binding processes and phase behaviors.

The integration of sophisticated algorithms like MIST with molecular dynamics simulations has enabled quantitative analysis of configurational entropy contributions across diverse systems, from protein-protein interactions to dynamically disordered molecular crystals. These approaches reveal the significant role of correlation terms often neglected in simplified treatments and provide a more complete picture of the entropy changes driving molecular recognition and assembly.

As computational methodologies continue to advance, incorporating increasingly accurate treatments of anharmonicity and dynamic disorder, our ability to predict and manipulate configurational entropy will further enhance rational design in pharmaceutical development and materials engineering. The integration of these computational insights with experimental approaches promises to unlock new opportunities for controlling molecular interactions through entropy engineering.

The binding affinity and spontaneity of intermolecular interactions, a cornerstone in drug discovery and molecular biology, are governed by the delicate balance of enthalpic and entropic forces as defined by the Gibbs free energy equation, ΔG = ΔH - TΔS. While often overshadowed by the more intuitive concept of enthalpy, the loss of configurational entropy (ΔSconf) of a ligand upon binding to its protein target frequently constitutes the primary thermodynamic barrier to association. This in-depth technical guide explores the central, and often decisive, role of ΔSconf in spontaneous binding. We elucidate the theoretical underpinnings, detail advanced computational and experimental methodologies for its quantification, and present quantitative data from seminal studies. Framed within the context of a broader thesis on the role of configurational entropy in intermolecular interactions research, this review provides researchers and drug development professionals with the foundational knowledge and practical protocols necessary to navigate and leverage this critical thermodynamic parameter.

Molecular recognition, the specific and reversible binding between a protein and a ligand, is fundamental to virtually all biological processes, from enzyme catalysis to cellular signaling [6]. The formation of a protein-ligand complex is a spontaneous process only if the associated change in Gibbs free energy (ΔG) is negative. The Gibbs free energy equation, ΔG = ΔH - TΔS, elegantly partitions this energy into its constituent drivers: the change in enthalpy (ΔH), representing the net strength of molecular interactions, and the change in entropy (TΔS), representing the net change in system disorder, scaled by temperature [7]. A deep understanding of this equation is paramount for rational drug design, where the goal is to engineer ligands that achieve a highly negative ΔG.

The entropic term, -TΔS, is multifaceted. The total entropy change upon binding, ΔS_total, is a composite of several contributions:

• Configurational Entropy (ΔS_conf): The loss of rotational and translational freedom of the ligand upon moving from a 3D solution to a confined binding pocket, coupled with a reduction in the conformational flexibility of both the ligand and the protein.
• Solvation Entropy (ΔS_solv): The change in the entropy of the water molecules surrounding the binding partners, often a major favorable driving force due to the release of ordered water molecules from the interface into the bulk solvent [8].

This guide focuses on ΔSconf, a quantity that is almost always unfavorable for binding (i.e., ΔSconf < 0) as the ligand loses degrees of freedom. Overcoming this large entropic penalty is a key challenge. In many cases, a sufficiently favorable, negative ΔH (e.g., from strong electrostatic or van der Waals interactions) or a highly favorable, positive ΔSsolv (from the hydrophobic effect) compensates for the configurational entropy loss. In certain systems, however, binding is entropy-driven, where a small ΔH is overcome by a large, favorable ΔSsolv, resulting in a negative ΔG [9] [6]. The following sections dissect the mechanisms, calculations, and experimental implications of this critical parameter.

Theoretical Framework: Deconstructing Configurational Entropy

The Statistical Mechanical Perspective

From a statistical mechanics viewpoint, entropy is a measure of the number of microscopic states, or microstates, accessible to a system. Configurational entropy is directly related to the probability distribution of a molecule's conformations. For a discrete set of states, it can be expressed as ( S{conf} = -kB \sum pi \ln pi ), where ( kB ) is Boltzmann's constant and ( pi ) is the probability of the system being in microstate i [10]. Upon binding, the diversity of accessible conformational states for the ligand and sometimes the protein active site is drastically reduced, leading to a significant decrease in Sconf and thus a negative ΔSconf.

The Thermodynamic Cycle and Absolute Binding Free Energy

The "double-decoupling method" provides a rigorous statistical mechanical framework for calculating absolute binding free energies (ΔG_bind) and decomposing them into entropic and enthalpic components [9]. This alchemical approach uses a thermodynamic cycle to avoid simulating the physical association process. The ligand is first decoupled from bulk solvent, followed by being coupled into the protein binding site in a series of non-physical steps. The absolute binding free energy is calculated as:

ΔGbind = ΔGgas→complex + ΔG_gas→gas - ΔG_gas→water [9]

Here, ΔG_gas→gas* is the free energy cost of restraining the ligand's position and orientation in the gas phase, which directly relates to the loss of its external (translational and rotational) entropy. The entropic component TΔS can be obtained from the temperature dependence of the free energy using the relationship ΔS = -(∂ΔG/∂T) [9].

Table 1: Key Entropic Contributions in Protein-Ligand Binding

Entropic Component	Typical Sign upon Binding	Physical Interpretation
Ligand Translational Entropy	Unfavorable (Negative ΔS)	Loss of 3D translational freedom in solution.
Ligand Rotational Entropy	Unfavorable (Negative ΔS)	Loss of rotational freedom in solution.
Ligand Conformational Entropy	Unfavorable (Negative ΔS)	Reduction in the number of accessible bond rotations and angles.
Protein Conformational Entropy	Unfavorable (Negative ΔS)	Reduction in the flexibility of the protein's side chains or backbone upon ligand binding.
Solvent Reorganization Entropy	Favorable (Positive ΔS)	Gain in entropy from the release of ordered water molecules from the binding pocket and ligand surface into the bulk solvent.

The diagram below illustrates the thermodynamic cycle and key entropy changes involved in the double-decoupling method for calculating absolute binding free energy.

Computational Protocols for Quantifying ΔS_conf

Accurately calculating configurational entropy is a significant challenge in computational chemistry. Below are detailed protocols for two prominent methods.

The Double-Decoupling Method (DDM) with MD Simulations

The DDM, also known as alchemical free energy simulation, is considered a gold standard for calculating absolute binding free energies and their entropic components [9].

Detailed Protocol:

• System Preparation: Obtain the atomic coordinates of the protein-ligand complex from a database like the PDB. Parametrize the ligand using tools like antechamber (GAFF force field) and the protein/water using a standard force field (e.g., AMBER, CHARMM). Solvate the complex in a water box (e.g., TIP3P) and add ions to neutralize the system.

• Equilibration: Perform energy minimization to remove steric clashes. Heat the system to the target temperature (e.g., 300 K) and equilibrate first with positional restraints on heavy atoms, followed by a full unrestrained equilibration run under constant pressure (NPT ensemble).

• Production MD for Bound State: Run a long-scale (e.g., >100 ns) molecular dynamics simulation of the fully solvated complex in the NPT ensemble. Save snapshots at regular intervals (e.g., 100 ps) for analysis.

• Alchemical Transformation - Decoupling from Water:

  • The ligand in a water box is gradually decoupled from its environment. Its interactions with water are "turned off" in a series of windows (e.g., λ = 0.0, 0.1, ..., 1.0).
  • At each λ window, perform extensive sampling (MD/MC) to calculate the free energy change (ΔG_gas→water) using methods like Thermodynamic Integration (TI) or Free Energy Perturbation (FEP).

• Alchemical Transformation - Coupling to Protein:

  • The ligand, now in the gas phase, is gradually coupled into the protein binding site. Its interactions with the protein and any bound waters are "turned on" across similar λ windows.
  • Critical Step: Apply harmonic restraints to the ligand's center of mass to prevent it from drifting away from the binding site when its interactions are weak. The free energy cost of applying these restraints (ΔG_gas→gas*) is calculated analytically and accounts for the loss of translational and rotational entropy [9].
  • Calculate the free energy change (ΔG_gas*→complex) for this leg.

• Entropy Calculation:

  • To extract the total binding entropy (TΔS), repeat the entire DDM process at multiple temperatures (e.g., 290 K, 300 K, 310 K).
  • Use finite differences to compute the derivative: ΔSbind = - (ΔGbind(T2) - ΔG_bind(T1)) / (T2 - T1) [9].

The MM/GBSA Method and Normal Mode Analysis

MM/GBSA (Molecular Mechanics/Generalized Born Surface Area) is a more efficient, but less rigorous, end-point method that estimates binding free energy from snapshots of an MD simulation of the complex.

Detailed Protocol:

• Generate Trajectory: Run an MD simulation of the protein-ligand complex, as described in Steps 1-3 of the DDM protocol.

• Post-Processing and Truncation:

  • Extract hundreds or thousands of snapshots from the stable part of the trajectory.
  • To make entropy calculation feasible, truncate the system. A common strategy is to include only the ligand and all protein residues within a certain cutoff (e.g., 8-16 Ã…) from the ligand's center of mass [11]. A more advanced method involves creating a single, connected component that preserves the biological interface.

• Calculate Energy Components:

  • For each snapshot, the gas-phase energy (ΔE_MM) is calculated using molecular mechanics force fields.
  • The solvation free energy (ΔGsolv) is decomposed into polar (ΔGpol) and non-polar (ΔG_nonpol) components. The polar term is computed by solving the Generalized Born (GB) equation, while the non-polar term is often estimated from the solvent-accessible surface area (SASA).

• Entropy Calculation with Normal Mode Analysis (NMA):

  • Perform NMA on a subset of snapshots (or an average structure) from the truncated system.
  • NMA calculates the vibrational frequencies of the system, from which the configurational entropy (quasiharmonic approximation) is derived using statistical mechanics formulae.
  • Note: This calculation is computationally expensive and is often the bottleneck. Studies show that a significant reduction in the number of snapshots used for NMA may not drastically affect accuracy but can greatly lower computation time [11].

• Final Binding Free Energy Calculation:

  • The final estimate is an average over all snapshots: ΔGbind = ΔEMM + ΔGsolv - TΔSconf

Table 2: Comparison of Computational Methods for ΔS_conf Calculation

Method	Theoretical Basis	Advantages	Disadvantages	Typical Application
Double-Decoupling Method (DDM)	Statistical Mechanics / Alchemical Pathway	High theoretical rigor; Can decompose entropy explicitly; Gold standard for absolute ΔG.	Extremely computationally expensive; Convergence can be slow (error ≥2 kcal/mol [9]); Complex setup.	Detailed mechanistic studies of high-affinity drug candidates.
MM/GBSA with NMA	End-point / Empirical Solvation	Much faster than DDM; Provides energy decomposition; Suitable for larger systems.	Relies on quasiharmonic approximation, which can be inaccurate; Sensitive to truncation method; Less rigorous.	High-throughput virtual screening and binding pose ranking.
k-th Nearest Neighbor (kNN)	Information Theory / Density Estimation	Can provide absolute entropy from MD ensembles; Accounts for correlated motions.	Requires high-dimensional sampling; Can be sensitive to parameters.	Analyzing conformational entropy in protein folding and flexibility.

Case Studies and Quantitative Data

HIV-1 Protease Inhibitors: A Tale of Two Thermodynamics

A classic example highlighting the role of entropy is the binding of inhibitors to HIV-1 protease. Calculations using the DDM revealed stark contrasts:

• Nelfinavir (NFV): Binding is entropy-driven. The calculated ΔG_bind was in general agreement with experiment, showing a large favorable entropy change. This was attributed to a very favorable desolvation entropy (release of water from the hydrophobic binding site) that overwhelmingly compensated for the configurational entropy loss [9].
• Amprenavir (APV): Binding is driven by both enthalpy and entropy. The entropy change, while still favorable, was much less so than for Nelfinavir. The decomposition showed that Amprenavir binding benefited more from strong electrostatic interactions with the protein (enthalpy) [9].

Table 3: Experimental and Calculated Binding Energetics for HIV-1 Protease Inhibitors

Ligand	Experimental ΔG_bind (kcal/mol)	Calculated ΔG_bind (kcal/mol)	Driving Force	Key Entropic Insight from Calculation
Nelfinavir (NFV)	~ -12.5 [9]	~ -12 to -16 [9]	Primarily Entropy	Large favorable desolvation entropy dominates.
Amprenavir (APV)	~ -13.4 [9]	~ -13 to -17 [9]	Enthalpy & Entropy	Less favorable total entropy than NFV; stronger electrostatic enthalpy.

The Critical Role of Solvent Entropy

Beyond the configurational entropy of the solute, the entropy of the solvent water is a powerful driving force. Research applying the Asakura-Oosawa theory to protein folding and binding demonstrates that the translational entropy (TE) of water can be the dominant contributor to the free energy change [8]. When two hydrophobic surfaces on a protein and ligand come together, the excluded volumes for water molecules overlap. This overlap increases the total volume available for the translational movement of water molecules in the system, leading to a gain in their entropy and a consequent decrease in the system's free energy. This effect is particularly potent in biological systems due to the small size of water molecules and the complex geometries of binding interfaces, which can create large overlapping excluded volumes [8].

The following diagram visualizes the competing entropy changes that determine the spontaneity of a binding event, highlighting the critical, often decisive, role of solvent entropy.

Table 4: Key Research Tools for Investigating Configurational Entropy

Tool / Resource	Type	Primary Function	Application in ΔS_conf Research
AMBER	Software Suite	Molecular Dynamics Simulation	Performs MD equilibration/production runs for DDM and MM/GBSA; includes modules for alchemical free energy calculations (e.g., TI).
GROMACS	Software Suite	Molecular Dynamics Simulation	High-performance MD engine used to generate trajectories for subsequent entropy analysis with MM/GBSA or other methods.
Normal Mode Analysis (NMA)	Computational Algorithm	Entropy Calculation	Calculates the vibrational entropy of a molecular system from a set of snapshots; often integrated into MM/GBSA workflows.
Isothermal Titration Calorimetry (ITC)	Experimental Instrument	Measuring Binding Thermodynamics	Directly measures the ΔG, ΔH, and TΔS of binding in a single experiment, providing experimental validation for computational predictions.
Linear Interaction Energy (LIE)	Computational Method	Binding Affinity Estimation	A simpler, semi-empirical method to estimate ΔG_bind; less direct for entropy decomposition but useful for screening.
GBNSR6 Model	Implicit Solvent Model	Solvation Free Energy Calculation	A specific Generalized Born (GB) model used in MM/GBSA to compute the polar solvation component (ΔG_pol) efficiently and accurately [11].

Configurational entropy loss, ΔSconf, is a fundamental and unavoidable thermodynamic tax levied on every intermolecular binding event. Its significant unfavorable contribution means that spontaneous binding is always a story of compensation, whether through strong, specific enthalpic interactions or through the powerful, omnipresent drive of solvent entropy gain. For researchers and drug developers, moving beyond a simplistic focus on ligand-receptor interactions to embrace a holistic view that includes water and flexibility is no longer optional. The advanced computational protocols detailed here, such as the double-decoupling method and MM/GBSA, provide the means to quantify these effects. Integrating these insights into the rational design pipeline—for instance, by designing ligands that minimize conformational entropy loss through pre-organization or that optimally leverage hydrophobic desolvation—holds the key to developing the next generation of high-affinity, selective therapeutic agents. As a central theme in intermolecular interactions research, mastering the implications of ΔSconf is essential for translating structural knowledge into functional prediction and control.

Configurational entropy (Sconf) is a fundamental thermodynamic property that quantifies the disorder associated with the spatial arrangement of molecules in a material. This in-depth technical guide examines the role of Sconf across three physical states—crystalline, amorphous, and super-cooled liquids—with particular emphasis on its implications for intermolecular interactions research, especially in pharmaceutical and materials science applications. The crystalline state exhibits minimal configurational entropy due to its highly ordered, periodic structure. In contrast, amorphous solids and super-cooled liquids possess significantly higher Sconf, influencing their stability, molecular mobility, and functional properties. This whitepaper synthesizes current theoretical frameworks, experimental methodologies, and computational approaches for quantifying Sconf, providing researchers with practical tools for investigating its critical role in processes ranging from protein-ligand binding to the stabilization of amorphous drug formulations.

Configurational entropy is a measure of the number of accessible molecular arrangements, or microstates, available to a system due to its molecular configuration [10]. In the context of intermolecular interactions research, it provides a crucial link between molecular structure, dynamics, and thermodynamic stability. Unlike thermal entropy, which arises from the distribution of energy, configurational entropy stems from the diversity of spatial arrangements a molecule can adopt.

The formal definition of the configurational entropy for a single molecule or complex can be derived from the quasi-classical entropy integral [1]: [ S{config} = R \ln(8\pi^2 V^\circ) - R \int \rho(\vec{q}{int}) \ln [h^{3N} J(\vec{q}{int}) \rho(\vec{q}{int})] d\vec{q}{int} ] where R is the universal gas constant, (V^\circ) is the standard volume, ( \rho(\vec{q}{int}) ) is the probability density function, (J(\vec{q}_{int})) is the Jacobian of the internal coordinates, and h is Planck's constant.

In molecular systems, S_conf arises from various internal degrees of freedom, including bond rotations, vibrations, and large-scale conformational changes [10]. Its accurate estimation remains challenging due to the complexity of high-dimensional phase spaces and the necessity to account for correlated motions. Recent advances in computational methodologies, such as the application of the k-th nearest neighbour algorithm and force covariance techniques, have significantly improved our ability to extract absolute entropy values from dynamic ensembles [10].

Theoretical Foundations

Thermodynamic Relationships

The configurational entropy represents the difference in entropy between amorphous and crystalline states [12]: [ S{conf}(T) = S{amorph}(T) - S_{crystal}(T) ]

This relationship forms the basis for experimental determination of Sconf through calorimetric measurements. The corresponding configurational enthalpy and Gibbs free energy are defined as [12]: [ H{conf}(T) = H{amorph}(T) - H{crystal}(T) ] [ G{conf}(T) = H{conf}(T) - TS_{conf}(T) ]

These configurational properties can be calculated from their relationship with heat capacity: [ H{conf} = \Delta Hm + \int{Tm}^{T} C{p}^{conf} dT ] [ S{conf} = \Delta Sm + \int{Tm}^{T} \frac{C{p}^{conf}}{T} dT ] where ( \Delta Hm ) and ( \Delta Sm ) are the enthalpy and entropy of melting, respectively, and ( C_{p}^{conf} ) is the configurational heat capacity, defined as the difference between amorphous and crystalline heat capacities [12].

The Kauzmann Paradox and Glass Transition

The temperature dependence of configurational entropy reveals fundamental aspects of material behavior. If a super-cooled liquid maintained equilibrium below the glass transition temperature (Tg), its entropy would eventually fall below that of the crystalline state at the Kauzmann temperature (TK), violating thermodynamic laws [12]. This paradox is resolved by the glass transition, where the system falls out of equilibrium, preventing the entropy catastrophe.

The relationship between temperature and thermodynamic properties for different states is visualized below:

Figure 1: Thermodynamic relationship between states. At Tg, the super-cooled liquid falls out of equilibrium, forming a glass and avoiding the entropy catastrophe at TK.

Configurational Entropy Across Physical States

Crystalline State

In crystalline materials, molecules are arranged in a periodic, repeating lattice structure with minimal disorder. The configurational entropy approaches zero for perfect crystals, as only one microstate (or a very limited number of equivalent arrangements) is accessible. Any residual entropy in crystals typically arises from:

• Point defects: Vacancies, substitutions, or interstitial atoms
• Dislocations: Line defects disrupting the perfect lattice
• Polymorphism: Different crystalline packing arrangements

The highly constrained nature of crystalline materials makes them valuable reference states for calculating configurational entropy differences.

Amorphous State

Amorphous solids (glasses) possess significant configurational entropy frozen in below T_g. Unlike crystals, amorphous materials lack long-range order, with molecules trapped in a multitude of configurations. Key characteristics include:

• Non-equilibrium state: Glasses are metastable and undergo relaxation toward lower energy states over time
• Frozen disorder: The configurational entropy is largely immobilized below T_g
• Relaxation behavior: Physical aging occurs as the material slowly relaxes, reducing enthalpy and entropy without crystallization [12]

The high S_conf of amorphous materials contributes to their enhanced solubility and dissolution rates compared to crystalline counterparts, which is particularly valuable in pharmaceutical applications for poorly soluble drugs [12].

Super-Cooled Liquid State

Super-cooled liquids exist in a metastable equilibrium between the melting point (Tm) and glass transition temperature (Tg). They exhibit unique characteristics:

• High molecular mobility: Viscosity is significantly lower than in the glassy state (typically 10^(-3) - 10^(12) Pa·s) [12]
• Temperature-dependent Sconf: Configurational entropy decreases as temperature approaches Tg
• Cooperatively rearranging regions (CRR): According to Adam-Gibbs theory, the liquid consists of regions that rearrange cooperatively, with CRR size increasing as S_conf decreases [12]

Super-cooled liquids are crucial for understanding the glass formation process and crystallization tendencies of materials.

Table 1: Comparative Analysis of Configurational Entropy in Different Physical States

Property	Crystalline State	Amorphous State	Super-Cooled Liquid
Structural Order	Long-range periodic order	Short-range order only	Short-range order only
S_conf Magnitude	Minimal (approaches 0)	High (frozen below T_g)	High (temperature-dependent)
Molecular Mobility	Limited to vibrations/rotations	Very low below T_g	High (decreasing with cooling)
Thermodynamic State	Equilibrium	Non-equilibrium, metastable	Metastable equilibrium
Stability	Thermodynamically stable	Physically unstable	Kinetically stabilized
Experimental Access	Direct calorimetry	Calorimetry relative to crystal	Calorimetry, computational methods

Quantitative Data and Methodologies

Experimental Determination

Calorimetric Methods

Differential scanning calorimetry (DSC) provides the primary experimental approach for determining configurational entropy. The methodology involves [12]:

• Measure heat capacities: Determine C_p for both crystalline and amorphous forms across the temperature range of interest
• Calculate C_p^conf: Compute the difference between amorphous and crystalline heat capacities
• Integrate from melting point: [ S{conf}(T) = \Delta Sm + \int{Tm}^{T} \frac{C{p}^{conf}}{T} dT ] where ( \Delta Sm = \frac{\Delta Hm}{Tm} ) is the melting entropy

The configurational heat capacity (Cp^conf) follows a hyperbolic temperature dependence above Tg [12]: [ Cp^{conf} = \frac{K}{T} = Cp^{conf}(Tg) \frac{Tg}{T} ]

Table 2: Experimental Parameters for Configurational Entropy Determination

Parameter	Symbol	Measurement Technique	Critical Considerations
Glass Transition Temperature	T_g	DSC (midpoint of transition)	Heating rate dependence
Melting Temperature	T_m	DSC (onset of endotherm)	Purity effects
Enthalpy of Melting	ΔH_m	DSC (area under endotherm)	Reference standard calibration
Configurational Heat Capacity	C_p^conf	DSC (modulated mode preferred)	Accurate baseline determination
Heat Capacity Change at T_g	ΔC_p	DSC (step change height)	Distinguish from relaxation effects

Protocol: Calorimetric Determination of S_conf

Materials and Equipment:

• Differential scanning calorimeter with temperature modulation capability
• Hermetic pans for sample encapsulation
• Standard reference materials (e.g., indium, sapphire) for calibration
• 5-10 mg of crystalline and amorphous samples

Procedure:

• Calibrate DSC instrument for temperature and enthalpy using certified standards
• Load crystalline sample and perform temperature scan from 50°C below to 50°C above T_m at 10°C/min
• Measure heat capacity using modulated DSC with ±0.5°C amplitude and 60s period
• Quench cool the melt to form amorphous material (rate > 50°C/min)
• Scan amorphous sample using identical conditions to measure C_p of glass and super-cooled liquid
• Calculate Cp^conf as the difference between amorphous and crystalline Cp values
• Integrate Cp^conf/T from Tm to temperature of interest to obtain S_conf(T)

Data Analysis: [ S{conf}(T) = \frac{\Delta Hm}{Tm} + \int{Tm}^{T} \frac{Cp^{amorph}(T) - C_p^{crystal}(T)}{T} dT ]

Computational Approaches

Molecular Dynamics Simulations

Molecular dynamics (MD) simulations provide atomic-level insights into configurational entropy by sampling the accessible phase space of molecular systems [10]. Key methodologies include:

• k-th Nearest Neighbour (kNN) Algorithm: A statistical approach for estimating entropy by quantifying distances between data points in high-dimensional spaces [10]
• Mutual Information Expansion (MIE): Accounts for correlations between different degrees of freedom when calculating configurational entropy [10] [1]
• Maximum Information Spanning Tree (MIST): Advanced MIE variant that efficiently captures essential correlations in biomolecular systems [1]

These methods have been particularly valuable for dissecting the configurational entropy change of protein binding into contributions from molecular internal and external degrees of freedom [1].

Protocol: Configurational Entropy from MD Simulations

System Preparation:

• Construct molecular system with appropriate force field parameters
• Solvate in explicit water molecules using periodic boundary conditions
• Energy minimize and equilibrate using NPT ensemble (1 atm, temperature of interest)

Production Simulation:

• Run MD simulation for sufficient duration to sample relevant configurations (typically 100 ns - 1 μs)
• Save trajectories at appropriate intervals (10-100 ps) for entropy analysis
• Monitor convergence of entropy estimates with simulation time

Entropy Calculation (kNN Method):

• Define relevant degrees of freedom (torsional angles, translational, rotational)
• Calculate distances between configurations in the high-dimensional space
• Apply kNN algorithm to estimate probability densities: [ S \approx \frac{1}{N} \sum{i=1}^{N} \log \rho(\vec{x}i) + constant ]
• Account for correlated motions using MIE or MIST frameworks

The following diagram illustrates the workflow for computational determination of configurational entropy:

Figure 2: Computational workflow for S_conf calculation from MD simulations.

Applications in Intermolecular Interactions Research

Pharmaceutical Sciences

Configurational entropy plays a crucial role in amorphous drug formulation and stabilization. Key applications include:

• Solubility Enhancement: The higher free energy of amorphous systems ((G{conf} = H{conf} - TS_{conf})) increases solubility and dissolution rates [12]
• Physical Stability Prediction: Sconf influences molecular mobility through the Adam-Gibbs equation: [ \tau = \tau0 \exp\left(\frac{B}{TS_{conf}}\right) ] where Ï„ is the structural relaxation time [12]
• Crystallization Inhibition: Polymers in solid dispersions reduce molecular mobility partly by decreasing S_conf

The relationship between configurational entropy and molecular mobility explains why storage below Tg enhances stability but doesn't guarantee prevention of crystallization, as molecular motions still occur below Tg [12].

Biomolecular Interactions

In protein-ligand binding and protein-protein interactions, configurational entropy change is a central constituent of the free energy change [1]. Recent studies demonstrate that:

• Configurational entropy contribution can be of similar magnitude as solvent entropy contribution [1]
• Different coupling terms between internal and external degrees of freedom contribute significantly to overall configurational entropy change [1]
• NMR-based approaches for configurational entropy change estimation are supported by the finding that total entropy change can be approximated by rescaling the sum of uncoupled contributions from internal degrees of freedom [1]

These insights significantly impact computational drug design by helping overcome enthalpy/entropy compensation effects [1].

Advanced Materials

Phase-change materials (PCMs) represent another application where configurational entropy plays a critical role. In materials like antimony (Sb) and its alloys, liquid-state anomalies and fragility of super-cooled liquids influence their switching capabilities between amorphous and crystalline states [13]. The relationship between viscosity (η) and configurational entropy follows the Adam-Gibbs equation: [ \eta = \eta0 \exp\left(\frac{D}{TS{conf}}\right) ] where high fragility (strong temperature dependence of viscosity) correlates with unique crystallization behavior in PCMs [13].

Table 3: Research Reagent Solutions for Configurational Entropy Studies

Reagent/Material	Function	Application Context
Molecular Dynamics Software (GROMACS, AMBER, NAMD)	Simulates molecular trajectories for entropy calculation	Computational estimation of S_conf from simulated ensembles
Differential Scanning Calorimeter	Measures heat capacity differences between states	Experimental determination of S_conf via calorimetry
Hermetic Sealing pans	Encapsulates samples during thermal analysis	Prevents moisture loss/absorption during DSC measurements
Neural Network Potentials	Machine-learned interatomic potentials	Accelerated MD simulations with near-quantum accuracy (e.g., for antimony studies [13])
kNN Algorithm Software	Implements k-th nearest neighbor entropy estimation	Computational entropy from high-dimensional data
MIST Implementation	Calculates mutual information expansion terms	Captures correlated motions in entropy calculations of biomolecules [1]

Configurational entropy serves as a fundamental bridge between molecular structure, dynamics, and thermodynamic stability across crystalline, amorphous, and super-cooled liquid states. Its quantification through both experimental calorimetric methods and advanced computational approaches provides critical insights for intermolecular interactions research. In pharmaceutical sciences, understanding S_conf enables rational design of amorphous drug formulations with optimized stability and performance. In biomolecular interactions, it reveals the intricate balance between enthalpy and entropy that governs binding affinity. For advanced materials like phase-change systems, configurational entropy helps explain unusual liquid-state properties and crystallization behavior. As computational methodologies continue to advance, particularly through machine-learned potentials and efficient entropy estimation algorithms, our ability to probe and manipulate configurational entropy will further expand, enabling new breakthroughs in materials design and drug development.

Configurational entropy (Sconf), the excess entropy of the amorphous state over the crystalline state, is a pivotal thermodynamic parameter governing the behavior of amorphous pharmaceuticals. It sits at a critical intersection, simultaneously driving the enhanced solubility and dissolution properties that make amorphous forms attractive, while also influencing the molecular mobility that can lead to physical instability and recrystallization. This whitepaper delineates the dual role of Sconf, examining its quantification through calorimetric methods, its direct incorporation into stability models via the Adam-Gibbs equation, and its complex interplay with kinetic factors. For researchers and drug development professionals, a deep understanding of S_conf is not merely an academic exercise but a practical necessity for navigating the trade-offs between bioavailability and stability in amorphous solid dispersions, ultimately enabling a more rational design of robust, high-performance drug products.

In the realm of pharmaceutical sciences, the amorphous state of a drug substance offers a powerful strategy to overcome the solubility limitations of crystalline materials, which constitute a significant portion of modern drug pipelines. The amorphous form is characterized by a disordered, non-crystalline molecular arrangement, resulting in a state of higher energy. This elevated energy state manifests as excess thermodynamic properties, including configurational enthalpy (Hconf), Gibbs free energy (Gconf), and critically, configurational entropy (Sconf). Sconf is formally defined as the difference in entropy between the amorphous and the crystalline states of a compound (Sconf = Samorph - S_crystal) [12]. This parameter is more than a simple descriptor; it is a fundamental property involved in both the thermodynamic driving forces and the kinetic processes that dictate the stability and performance of amorphous pharmaceuticals.

The central challenge in formulating amorphous drugs lies in managing the inherent instability that accompanies their desirable solubility enhancement. The same high energy that favors rapid dissolution also provides a potent thermodynamic driving force for recrystallization, a process that negates the solubility advantage. The stability of the amorphous state is therefore not guaranteed, and its prediction remains a complex challenge. Historically, research has oscillated between emphasizing kinetic parameters, such as molecular mobility, and thermodynamic parameters, such as the free energy difference, as the primary predictors of stability. Emerging from this discourse is the recognition that Sconf is a key bridging parameter, integral to both the thermodynamic and kinetic perspectives [14] [12]. Its role in the Adam-Gibbs theory directly links the configurational state of the system to its molecular mobility, making it a essential quantity for a holistic understanding of amorphous behavior. This whitepaper explores this critical balance, detailing how Sconf influences the solubility-stability paradox and providing methodologies for its quantification and application in rational formulation design.

Theoretical Foundations: The Dual Role of S_conf

S_conf is a critical parameter because it is not merely a static measure of disorder; it actively participates in the key processes that define the fate of an amorphous pharmaceutical. Its influence is twofold, governing both the "why" of recrystallization (thermodynamics) and the "how fast" (kinetics).

Thermodynamic Driving Force

The enhanced apparent solubility and dissolution rate of an amorphous drug are direct consequences of its elevated Gibbs free energy. The configurational free energy (Gconf) is calculated from the configurational enthalpy and entropy as shown in the equation below, which also provides the method for determining Hconf and S_conf from experimental heat capacity data [12]:

Where:

and ΔS_m = ΔH_m / T_m.

The larger the value of Gconf, the greater the thermodynamic driving force for dissolution. However, this same driving force also makes recrystallization thermodynamically favorable. The configurational entropy (Sconf) is a major component of this energy landscape. A high Sconf contributes to a high Gconf, which is beneficial for solubility but detrimental to physical stability, as the system will seek to reduce this excess energy by reverting to the crystalline state [12].

Kinetic Involvement and the Adam-Gibbs Theory

While thermodynamics dictates the direction of change, kinetics controls the rate. The molecular mobility of an amorphous system, often expressed as its reciprocal, the relaxation time (Ï„), is a key kinetic factor determining the rate of crystallization. The most common theory linking thermodynamics to kinetics is the Adam-Gibbs (AG) theory, which introduces the concept of cooperatively rearranging regions (CRRs). The AG theory posits that molecular rearrangement occurs in coordinated regions, and the size of these regions is determined by the configurational entropy. The central equation is:

where Ï„_0 and C are constants [14] [12].

Upon cooling, the Sconf decreases, causing the size of the CRRs to increase. This increasing cooperativity slows down molecular motion. The AG equation demonstrates that Sconf is not just a thermodynamic quantity but is the fundamental link between the thermodynamic state of the system and its molecular mobility. A system with low Sconf will have higher molecular mobility (shorter Ï„), making it more susceptible to crystallization, even if the thermodynamic driving force is significant [12]. This dual role makes Sconf a critical parameter for any comprehensive stability assessment.

Quantitative Analysis: Correlating S_conf with Stability and Mobility

Empirical studies across multiple drug compounds have quantitatively established the significant, and sometimes dominant, role of S_conf in predicting amorphous stability. Moving beyond case studies to larger sample sets provides robust evidence for its utility.

Table 1: Correlation of Thermodynamic and Kinetic Parameters with Physical Stability (n=12 drugs)

Parameter Category	Specific Parameter	Correlation with Stability (r²)	Key Finding
Kinetic	Relaxation Time (Ï„) below Tg	No correlation	Stability predictions based on relaxation time alone may be inadequate [14].
Kinetic	Fragility Index below Tg	No correlation	Fragility values spanned 8.9 to 21.3, but did not correlate with stability [14].
Thermodynamic	Configurational Entropy (S_conf) above Tg	0.685 (Strongest correlation)	S_conf exhibited the strongest correlation with observed physical stability [14].
Thermodynamic	Configurational Enthalpy (H_conf) above Tg	Reasonable correlation	Correlated with stability, but weaker than S_conf [14].

A study investigating 12 amorphous drugs found that below the glass transition temperature (Tg), traditional kinetic parameters like relaxation time and fragility index showed no correlation with the observed physical stability. In contrast, thermodynamic parameters, particularly the configurational entropy, demonstrated a much stronger relationship with stability above Tg [14]. This challenges the conventional wisdom that molecular mobility is the sole dominant factor and highlights the necessity of incorporating thermodynamic measurements.

Further supporting this, a study of five structurally diverse compounds (ritonavir, ABT-229, fenofibrate, sucrose, and acetaminophen) revealed that the crystallization tendency under non-isothermal conditions was most closely related to the entropic barrier to crystallization and the molecular mobility. The entropic barrier is inversely related to the probability that molecules are in the proper orientation for crystallization. For instance, ritonavir, which did not crystallize, possessed the highest entropic barrier, while acetaminophen and sucrose, which crystallized readily, had the lowest entropic barriers. This indicates that even with a significant thermodynamic driving force for crystallization, a high entropic barrier can impart stability by making the molecular alignment required for nucleation less probable [15].

Table 2: Ranking of Factors Influencing Crystallization Tendency in Five Model Compounds [15]

Compound	Crystallization Observed?	Configurational Free Energy (G_c) Driving Force	Entropic Barrier to Crystallization	Molecular Mobility (1/Ï„)
Ritonavir	No	Highest	Highest	Lowest
Acetaminophen	Yes	Medium	Lowest	Highest
Fenofibrate	Yes	Medium	Medium	Medium
Sucrose	Yes	Low	Lowest	Medium
ABT-229	Yes	Lowest	Medium	Low

Experimental Protocols and Methodologies

The accurate determination of S_conf is foundational to its application. The primary methodology relies on calorimetric measurements to obtain the heat capacity data required for the calculations outlined in Section 2.1.

Determination of Configurational Heat Capacity (Cp_conf)

Objective: To measure the heat capacities of the crystalline and amorphous forms of a drug substance as a function of temperature. Instrumentation: Modulated Temperature Differential Scanning Calorimetry (MTDSC) is the preferred technique due to its ability to separate reversing and non-reversing thermal events. Procedure:

• Calibration: Calibrate the DSC instrument for temperature and heat capacity using standard references (e.g., sapphire).
• Sample Preparation:
  • Crystalline Sample: Use the pure, stable crystalline form of the drug. Gently grind if necessary to ensure good thermal contact.
  • Amorphous Sample: Prepare the amorphous form directly in a DSC pan. This can be achieved by melting the crystalline sample and subsequently quenching it rapidly (e.g., with liquid nitrogen) to prevent recrystallization.
• Measurement:
  • For both crystalline and amorphous samples, perform MTDSC scans from a temperature well below the glass transition (Tg) to above the melting point (Tm) at a controlled heating rate (e.g., 1-2 K/min).
  • Ensure the modulation amplitude and period are appropriately set to obtain clear reversing heat flow signals.
• Data Analysis:
  • Extract the reversing heat capacity (Cp) as a function of temperature for both the amorphous (Cpamorph) and crystalline (Cpcrystal) forms.
  • The configurational heat capacity is calculated as: Cp_conf = Cp_amorph - Cp_crystal [12]. It is critical to note that Cp_conf is not the same as the heat capacity change (ΔCp) at the glass transition.

Calculation of Configurational Entropy (S_conf)

Objective: To compute the configurational entropy (Sconf) from the melting parameters and the measured Cpconf. Data Requirements: Enthalpy of fusion (ΔHm), Melting temperature (Tm), and the Cp_conf values from the previous protocol. Procedure:

• Obtain Fusion Parameters: From a standard DSC scan of the crystalline material, determine the melting enthalpy (ΔHm) and melting temperature (Tm). Calculate the melting entropy: ΔS_m = ΔH_m / T_m.
• Integrate Cp_conf: Using the data from the MTDSC experiments, perform the integrations as per the equations in Section 2.1:
  • H_conf(T) = ΔH_m + ∫_{T_m}^{T} Cp_conf dT
  • S_conf(T) = ΔS_m + ∫_{T_m}^{T} (Cp_conf / T) dT
• Consider Temperature Dependence: Note that above Tg, the configurational heat capacity may not be constant. Its temperature dependence has been described by a hyperbolic relation: Cp_conf(T) = Cp_conf(Tg) * (Tg / T) [12]. The choice of model for Cpconf above Tg can influence the accuracy of the calculated Sconf at temperatures far from Tm.

The following workflow diagram illustrates the experimental and computational pathway for determining S_conf and its application in stability assessment:

Figure 1: Experimental Workflow for Determining Configurational Entropy. This diagram outlines the key steps from sample preparation to the application of S_conf in stability prediction.

The Scientist's Toolkit: Essential Reagents and Materials

The experimental determination of S_conf and the formulation of stable amorphous systems require a specific set of reagents and analytical tools. The following table details key materials used in this field.

Table 3: Research Reagent Solutions for Amorphous Pharmaceutical Studies

Category	Item / Technique	Function / Purpose
Model Compounds	Ritonavir, Fenofibrate, Acetaminophen, Sucrose, Indomethacin	Structurally diverse model drugs for studying crystallization behavior and validating thermodynamic models [15] [12].
Polymeric Carriers	KOLIONA64 (KVA64), KOLIV17ONA17 (K17PF), HPMCAS, Eudragit EPO	Polymers used to form amorphous solid dispersions (ASDs) to enhance physical stability by increasing Tg and providing kinetic stabilization [16].
Primary Analytical Instrument	Modulated Temperature DSC (MTDSC)	Measures heat capacity (Cp) of amorphous and crystalline forms as a function of temperature, which is the primary data source for calculating Sconf, Hconf, and Tg [15] [12].
Theoretical Models	Adam-Gibbs (AG) Equation, Vogel-Tammann-Fulcher (VTF) Equation	Used to calculate molecular relaxation times (Ï„) by incorporating S_conf, linking thermodynamic state to kinetic stability [14] [12].
Solubility/Miscibility Modeling	Flory-Huggins (FH) Theory, PC-SAFT, Hansen Solubility Parameters	Predicts the miscibility and phase behavior of API-polymer blends, which is critical for designing stable ASDs [16].
Fmoc-NMe-Val-Val-Dil-Dap-OH	Fmoc-NMe-Val-Val-Dil-Dap-OH, MF:C45H66N4O9, MW:807.0 g/mol	Chemical Reagent
VUF11418	VUF11418, MF:C25H31I2N, MW:599.3 g/mol	Chemical Reagent

Integrated Stability Framework: Bridging Thermodynamics and Kinetics

The evidence clearly indicates that a singular focus on either thermodynamics or kinetics is insufficient for predicting the physical stability of amorphous pharmaceuticals. An effective framework must integrate both. The following diagram synthesizes the interplay of the key factors discussed, with S_conf at its core.

Figure 2: The Dual Role of S_conf in Amorphous Pharmaceuticals. This framework illustrates how a high S_conf simultaneously drives beneficial solubility and, through its effect on mobility, can enhance stability, while also creating a thermodynamic instability.

This framework reveals the critical balance. A high S_conf is a double-edged sword:

• On one hand, it increases the thermodynamic driving force for crystallization, which is detrimental to stability.
• On the other hand, according to the Adam-Gibbs theory, a high S_conf acts to reduce molecular mobility, which is beneficial for stability.

The overall stability of a specific amorphous drug will depend on which of these opposing influences is dominant. For instance, a compound like ritonavir possesses a high Sconf, which results in a high entropic barrier to crystallization and low mobility, making it inherently stable despite a large thermodynamic driving force [15]. This integrated view explains why a parameter like Sconf, which sits at the nexus of these competing effects, shows a stronger correlation with stability than kinetic parameters alone.

Configurational entropy is a fundamental property that critically influences the delicate balance between solubility and stability in amorphous pharmaceuticals. The empirical data demonstrates that Sconf can be a more robust predictor of physical stability than kinetic parameters like relaxation time. Its unique position, embedded in both the thermodynamic equations that define the driving force for crystallization and the Adam-Gibbs equation that governs molecular mobility, makes it an indispensable parameter for rational formulation design. For researchers aiming to develop viable amorphous drug products, the experimental protocols for determining Sconf, combined with the integrated stability framework, provide a powerful approach to navigate the inherent challenges. Moving forward, the continued integration of S_conf into predictive models and formulation strategies will be essential for unlocking the full potential of amorphous systems to deliver poorly soluble drugs, thereby accelerating the development of critical new therapies.

Quantifying Disorder: Computational and Experimental Methods for Measuring S_conf

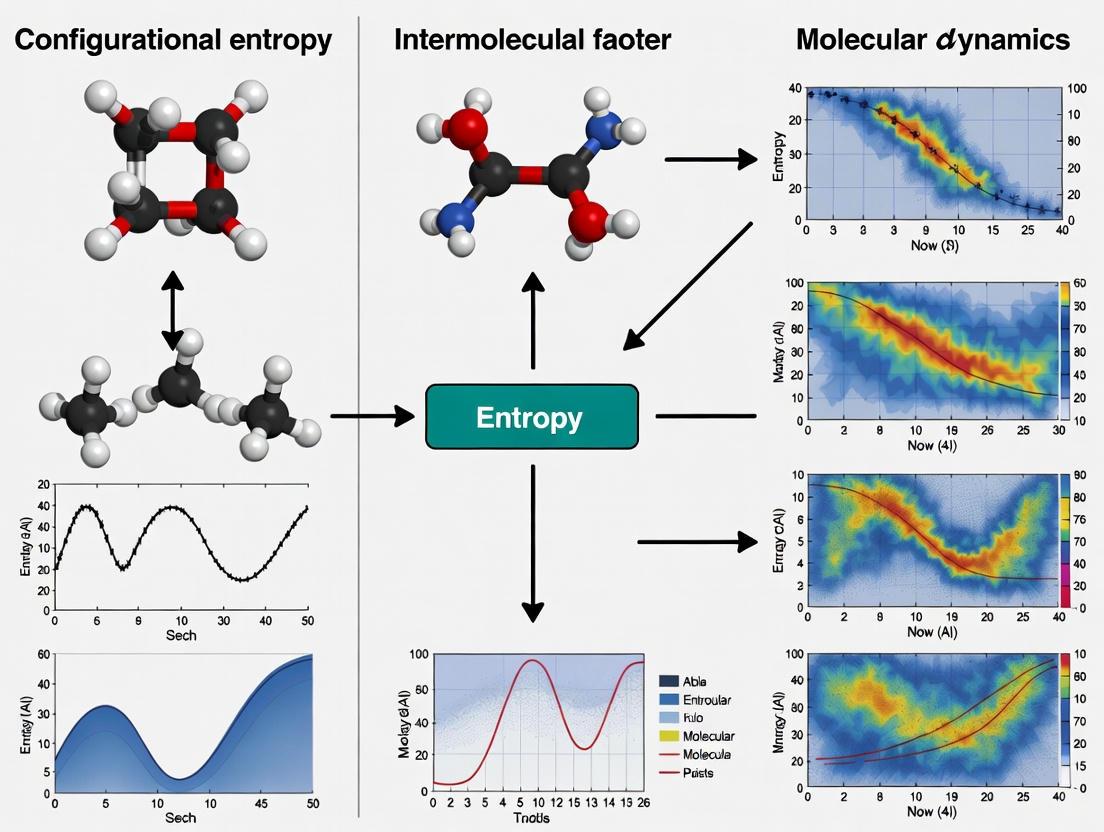
Configurational entropy, a measure of the number of ways a molecular system can arrange its structure while maintaining the same energy, plays a fundamental role in governing intermolecular interactions. In molecular dynamics (MD) simulations, the calculation of entropy from trajectory data remains one of the most challenging yet crucial aspects for predicting binding affinities, protein stability, and drug-receptor interactions. The trajectory of a MD simulation—a time-series of atomic positions and velocities—encodes the information about the system's exploration of its conformational landscape, from which entropy can be derived [17]. Unlike enthalpy, which can be directly computed from instantaneous coordinates, entropy quantification requires statistical mechanical treatment of the entire trajectory to assess the probability of visited states [18]. This technical guide provides an in-depth examination of trajectory analysis methodologies for entropy calculation, framed within the critical context of understanding configurational entropy's role in intermolecular interactions research for drug development.

Theoretical Foundation: Configurational Entropy in Intermolecular Interactions

The Role of Entropy in Biomolecular Recognition

Intermolecular interactions, particularly in drug binding, are governed by the balance between enthalpy (direct molecular interactions) and entropy (disorder and freedom). While enthalpy contributions from hydrogen bonds, electrostatic, and van der Waals interactions are more intuitively understood, the configurational entropy component of binding free energy represents a critical determinant that can dominate the binding affinity [18]. When a ligand binds to its receptor, the system typically loses configurational entropy due to restricted motion, which opposes binding. However, this loss can be offset by the release of ordered water molecules (solvent entropy gain) and by pre-organization of the binding partners [18]. Neglecting entropy in binding free energy calculations can lead to severely violated thermodynamic principles and inaccurate predictions [18].

The Computational Challenge of Entropy

The fundamental challenge in calculating entropy from MD trajectories lies in the accurate characterization of the system's phase space volume exploration. For a biomolecular system with thousands of atoms, the conformational space is astronomically large, and typical MD simulations (nanoseconds to microseconds) sample only a minuscule fraction of it [17]. Additionally, unlike solids with defined reference states or gases with simple statistical distributions, liquids and biomolecules exhibit complex interplay between strong interatomic interactions and dynamic disorder, making entropy particularly difficult to compute [19]. This has historically led to the perception that entropy cannot be accurately determined from MD simulations, prompting the development of various alternative strategies [19].

Methodologies for Entropy Calculation from MD Trajectories

End-State Methods and the Entropy Challenge

End-state methods, such as MM/PBSA and MM/GBSA, are widely used for binding free energy calculations in drug discovery. These methods estimate the free energy difference between bound and unbound states using the thermodynamic cycle shown in Figure 1, with entropy included as a separate term in the equation [18]:

ΔGbinding (solvated) = ΔGsolvated, complex - (ΔGsolvated, receptor + ΔGsolvated, ligand)

Where each ΔG term is calculated as: ΔGtotal (solvated) = Egas, phase + (ΔGsolvation - T × Ssolute)

In this formulation, the entropy (S) must be explicitly calculated, which presents the primary computational challenge [18].

Figure 1. Entropy Calculation Workflow. Decision flow for selecting and implementing primary entropy calculation methods from MD trajectories.

Normal Mode Analysis (NMA)

Normal Mode Analysis calculates vibrational entropy by approximating the potential energy surface as harmonic around a local minimum. The method involves [18]:

• Energy Minimization: Bringing the system to the nearest local energy minimum using algorithms like steepest descent, conjugate gradient, or Newton-Raphson methods.
• Hessian Matrix Construction: Calculating the matrix of second derivatives of potential energy with respect to atomic coordinates, either through analytical derivatives or finite differences.
• Diagonalization: Mass-weighting the Hessian to form the dynamical matrix and diagonalizing it to obtain eigenvalues (vibrational frequencies) and eigenvectors (atomic displacement patterns).

The entropy is then calculated from the vibrational frequencies using standard statistical mechanical formulas. Although NMA provides valuable insights, it suffers from several limitations: high computational cost that scales approximately as (3N)³ where N is the number of atoms, assumption of harmonicity that fails for flexible molecules at higher temperatures, and challenges in adequately accounting for solvent effects [18].

Quasi-Harmonic Analysis (QHA)

Quasi-Harmonic Analysis addresses some NMA limitations by approximating the potential energy surface as harmonic based on the fluctuations observed throughout an MD trajectory rather than at a single minimum [18]. The methodology involves:

• Covariance Matrix Calculation: Constructing the mass-weighted covariance matrix of atomic positional fluctuations from the trajectory.
• Diagonalization: Obtaining eigenvalues of the covariance matrix that represent the principal modes of motion.
• Frequency Estimation: Treating these eigenvalues as equivalent to harmonic frequencies for entropy calculation.

While QHA is less computationally intensive than NMA for the analysis phase, it requires extensive trajectory sampling to accurately estimate the covariance matrix, increasing the initial simulation burden [18].

Zentropy Theory: A Novel Approach

A recent breakthrough methodology integrates zentropy theory with MD simulations to enable rapid entropy calculation from a single trajectory [19]. This approach addresses the configurational entropy challenge by:

• Local Configuration Identification: Analyzing the MD trajectory to identify and classify local structural configurations and atomic distributions.
• Probability Calculation: Determining the probabilities of these local configurations within the trajectory.
• Multiscale Entropy Summation: Calculating total entropy as a sum of configurational, vibrational, and thermal electronic components across multiple scales.

The zentropy approach has demonstrated remarkable accuracy in predicting entropies and melting points for complex systems like fluoride and chloride molten salts, showing excellent agreement with experimental data [19]. This method offers significant computational advantages, requiring smaller supercells and fewer temperature points compared to traditional methods like SLUSCHI (Solid and Liquid in Ultra Small Coexistence with Hovering Interfaces) [19].

Comparative Analysis of Methods

Table 1: Quantitative Comparison of Entropy Calculation Methods

Method	Computational Scaling	Accuracy Limitations	Best Use Cases	Key Requirements
Normal Mode Analysis (NMA)	(3N)³ for diagonalization	Fails for anharmonic systems; harmonic approximation	Small systems (<500 atoms); local minima	Well-minimized structure; harmonic assumption
Quasi-Harmonic Analysis (QHA)	N² for covariance matrix	Requires extensive sampling; quasi-harmonic approximation	Larger systems with good sampling	Long trajectories; converged fluctuations
Zentropy Theory	Varies with configuration space	Depends on local structure identification	Complex liquids; phase transitions	Single trajectory; local configuration analysis
MM/PBSA/GBSA	Linear with number of frames	Neglects certain entropy contributions; implicit solvent	Binding affinity screening; relative comparisons	Ensemble of snapshots; implicit solvent model

Experimental Protocols and Implementation

Protocol for NMA-Based Entropy Calculation

Software Requirements: AMBER, GROMACS, or NAMD with NMA capabilities [18]

Step-by-Step Procedure:

• Trajectory Preprocessing:

  • Extract frames from MD trajectory at appropriate intervals (e.g., every 100ps)
  • Remove rotational and translational motions through alignment
  • Ensure trajectory covers relevant conformational space

• Energy Minimization:

  • Apply steepest descent algorithm for initial minimization (1000-5000 steps)
  • Switch to conjugate gradient for precise convergence (5000-10000 steps)
  • Use convergence criteria of 0.1 kcal/mol/Ã… for gradient

• Hessian Matrix Calculation:

  • Compute second derivatives using finite differences (displacements of 0.01Ã…)
  • Apply mass-weighting to construct dynamical matrix
  • For large systems, use iterative methods for partial diagonalization

• Entropy Calculation:

  • Diagonalize dynamical matrix to obtain vibrational frequencies
  • Apply quantum harmonic oscillator formula for entropy: Svib = kB Σ [ (hνi/kBT) / (e^(hνi/kBT) - 1) - ln(1 - e^(-hνi/kBT)) ]
  • Sum contributions from all non-zero frequencies

Validation Steps:

• Check for negative frequencies (indicative of insufficient minimization)
• Verify convergence with different minimization protocols
• Compare with experimental data when available

Protocol for Zentropy-Based Entropy Calculation

Software Requirements: Custom implementation as described by Hong and Liu [19]

Step-by-Step Procedure:

• Trajectory Analysis:

  • Run AIMD or classical MD simulation with appropriate ensemble (NPT recommended)
  • Sample configurations at regular intervals (e.g., every 100fs)
  • Identify local structural configurations using neighbor analysis

• Configuration Probability Calculation:

  • Classify local atomic environments using Voronoi tessellation or coordination number analysis
  • Calculate occurrence probabilities P_i for each local configuration type
  • Compute configurational entropy: Sconfig = -kB Σ Pi ln Pi

• Vibrational Entropy Calculation:

  • Calculate vibrational density of states from velocity autocorrelation function
  • Integrate with proper quantum correction for vibrational entropy

• Total Entropy Computation:

  • Sum configurational, vibrational, and electronic entropy components
  • Apply multiscale zentropy theory formulation [19]

Validation Steps:

• Verify probability convergence with trajectory length
• Test sensitivity to local configuration definition
• Compare with known thermodynamic data for reference systems

Table 2: Research Reagent Solutions for Entropy Calculations

Tool/Resource	Type	Function in Entropy Analysis	Implementation Considerations
AMS Trajectory Analysis [20]	Software Suite	Radial distribution functions, mean square displacement, ionic conductivity	Supports KFF trajectory files; automated range processing
FastMDAnalysis [21]	Python Package	Automated analysis of RMSD, RMSF, Rg, H-bonding, PCA	Reduces scripting overhead by >90%; unified interface
Desmond [22]	MD Engine	Production of MD trajectories with OPLS forcefield	Triplicate simulations recommended for statistical significance
Zentropy Code [19]	Theoretical Framework	Configurational entropy from single MD trajectory	Requires local structure identification algorithms
AMBER [18]	MD Suite	Normal mode analysis with steepest descent/conjugate gradient minimization	Computational cost scales cubically with system size
ROWAN [23]	Commercial Platform	Machine learning-accelerated property predictions	Proprietary neural network potentials (Egret-1, AIMNet2)

Case Studies in Intermolecular Interactions Research

SARS-CoV-2 Spike Protein Variant Analysis

In studies of SARS-CoV-2 spike protein binding to hACE2, MD simulations with entropy calculations revealed how mutations affect binding affinity. For the B.1.617 variant (Delta), triplicate 500ns simulations of wild-type and mutant (E484Q, L452R, and double mutant) structures provided insights into enhanced binding mechanisms [22]. The E484Q mutation was found to disrupt a conserved salt bridge with Lys31 of hACE2, while L452R introduced a charged patch enabling increased electrostatic attraction [22]. MM-GBSA calculations incorporating entropy contributions explained the variant's higher transmissibility and immune escape capability.

Butanol Isomers and Intermolecular Interactions

Systematic studies on alkyl and phenyl substituted butanol isomers combined XRD, FTIR, BDS, and MD simulations to understand hydrogen bonding patterns and molecular dynamics [24]. The research demonstrated clear differences in dynamic and static properties between primary and secondary alcohols, including variations in H-bond strength, distribution, dissociation enthalpy, glass transition temperature, and Kirkwood factor [24]. These findings highlight how subtle structural changes affect configurational entropy and intermolecular interaction networks.

Molten Salt Thermodynamics

The zentropy approach demonstrated remarkable accuracy in predicting entropies, enthalpies, and melting points of 25 binary and ternary fluoride and chloride molten salts [19]. By analyzing probabilities of local structural configurations from AIMD trajectories, researchers achieved rapid computation of entropy in both solids and liquids—addressing a long-standing challenge in computational thermodynamics [19]. The method's success with complex ionic systems suggests promising applications for biomolecular binding entropy calculations.

Advanced Applications and Future Directions

Machine Learning Accelerated Entropy Calculations

Emerging platforms like Rowan Scientific's Egret-1 neural network potentials match or exceed quantum-mechanics-based simulation accuracy while running orders-of-magnitude faster [23]. Such approaches enable high-throughput entropy calculations previously impractical with conventional methods. Similarly, graph neural network models have been developed to predict melting points across diverse materials, demonstrating ML's potential in entropy-related property prediction [19].

Probing Environmental Effects on Molecular Rotation

Advanced experimental techniques now enable real-time tracking of laser-driven rotational dynamics of single molecules affected by neighboring atoms, providing unprecedented insights into environmental effects on molecular rotation [25]. Studies of Nâ‚‚-Ar dimers using coincident Coulomb explosion imaging have visualized how neighboring atoms hinder molecular rotation, suppressing alignment and accelerating decay of rotational coherence [25]. These findings provide quantitative benchmarks for validating entropy calculations from MD simulations.

Automated Analysis Workflows

Tools like FastMDAnalysis represent a movement toward standardized, reproducible analysis pipelines that encapsulate complex trajectory analysis into unified frameworks [21]. In a case study analyzing 100ns simulation of Bovine Pancreatic Trypsin Inhibitor, the software performed comprehensive conformational analysis (RMSD, RMSF, Rg, H-bonding, SASA, secondary structure, PCA, and clustering) in under 5 minutes with a single command [21]. Such automation makes sophisticated entropy calculations accessible to non-specialists and enhances reproducibility.

This whitepaper provides an in-depth technical examination of Mutual Information Expansion (MIE) and the Maximum Information Spanning Tree (MIST) algorithm, advanced computational frameworks essential for quantifying configurational entropy in biomolecular systems. Within intermolecular interactions research, particularly in computational drug discovery, accurately calculating entropy changes resulting from processes like protein binding remains a significant challenge. These frameworks enable the decomposition of entropy into individual contributions from various molecular degrees of freedom, offering critical insights that traditional methods often overlook. This guide details their mathematical foundations, provides actionable protocols for their application, and demonstrates their critical role in elucidating the thermodynamic drivers of molecular recognition and binding, thereby empowering researchers to make more informed decisions in therapeutic development.

In biomolecular processes, the configurational entropy of a solute is a fundamental component of the total free energy. For noncovalent binding events, the associated change in configurational entropy, ΔS, can substantially influence the binding affinity [1]. Traditional assumptions held that configurational entropy was negligible compared to solvent entropy effects; however, experimental and computational studies have confirmed that its contribution is significant and can be on a similar scale to entropy changes in the solvent [1] [26]. The central challenge is that configurational entropy depends on the complete joint probability density function over all the solute's internal coordinates. Intuitively, greater correlation among conformational degrees of freedom implies less freedom to explore configurational space, resulting in lower entropy [26].

Information theory, pioneered by Claude Shannon, provides the tools to dissect this complex problem. The key quantity is Mutual Information (MI), which measures the mutual dependence between two random variables. In units of bits or nats, it quantifies the amount of information obtained about one variable by observing the other [27]. For two discrete random variables X and Y, MI is defined as:

where ( P{(X,Y)} ) is the joint probability distribution, and ( PX ) and ( P_Y ) are the marginal distributions [27]. A fundamental property is that ( I(X;Y) = 0 ) if and only if X and Y are independent. Within the context of molecular conformations, MI provides a direct way to quantify correlations between different internal coordinates, such as torsional angles.

Mathematical Foundations of MIE and MIST

Mutual Information Expansion (MIE)

The Mutual Information Expansion offers a rigorous framework to break down the total configurational entropy of a system with N degrees of freedom into a sum of terms of successively higher orders. The expansion disentangles the contributions from individual variables (first-order), pairs of variables (second-order), triplets (third-order), and so forth.

The total entropy ( S ) for the full set of variables ( {X1, X2, ..., X_N} ) is given by the MIE as follows [26]:

In this expression:

• ( \sum S(X_i) ) is the sum of the first-order entropies, which would be the total entropy if all degrees of freedom were independent.
• ( \sum I(Xi;Xj) ) is the sum of the pairwise mutual information terms, correcting for the correlations between all pairs of variables.
• The higher-order terms (e.g., ( I(Xi;Xj;X_k) )) further correct for correlations among three or more variables simultaneously.

The MIE elegantly captures the intuitive notion that correlation reduces the total configurational entropy relative to the sum of individual entropies. Calculating all terms in this series becomes computationally intractable for large biomolecules; therefore, the expansion is often truncated at the second or third order.

Maximum Information Spanning Tree (MIST) Approximation

The Maximum Information Spanning Tree (MIST) algorithm provides a powerful and efficient alternative to the full MIE. Instead of trying to compute all possible higher-order correlations, MIST constructs a tree structure that captures the most significant pairwise correlations among the variables.

The MIST approximation for the total entropy is given by [1] [26]:

where ( T ) represents the set of edges in the maximum information spanning tree. This tree is built by selecting the ( N-1 ) pairwise mutual information terms that are the largest, thereby forming a connected, acyclic graph that includes all variables. The MIST framework effectively captures the strongest correlations in the system while remaining computationally feasible for large-scale studies, such as analyzing entropy changes in protein-protein binding [1].

Table 1: Key Formulations of Entropy in MIE and MIST Frameworks

Framework	Mathematical Formulation	Core Principle	Computational Cost
Full Configurational Entropy	( S = -k_B \int \rho(\vec{q}) \ln \rho(\vec{q}) d\vec{q} ) [26]	Directly integrates over the full joint probability density.	Prohibitively high for large molecules.
Mutual Information Expansion (MIE)	( S{\text{full}} = S1 + S_{\text{full}}^{\text{corr}} ) [26]	Decomposes entropy into a series of terms of increasing correlation order.	Intractable for high-order terms.
Maximum Information Spanning Tree (MIST)	( S{\text{MIST}} = \sum S(Xi) - \sum{(i,j) \in T} I(Xi;X_j) ) [1] [26]	Approximates entropy using a tree of the strongest pairwise correlations.	Feasible and efficient for biomolecules.

Quantitative Analysis of Entropy Components

Recent large-scale molecular dynamics studies applying MIE and MIST to protein binding have yielded critical quantitative insights into the components of configurational entropy change (ΔS). These analyses often partition the degrees of freedom into external (rigid body rotations and translations) and internal (torsional angles, etc.) sets, further dissecting the coupling between them.

Research confirms that different coupling terms contribute significantly to the overall configurational entropy change, contrary to historical assumptions that they could be neglected [1]. For instance, in a study of various protein complexes, the uncoupled entropy change from internal degrees of freedom (ΔS₁𝒟) varied widely, as shown in Table 2. This suggests that the magnitude of individual terms is largely unpredictable a priori and requires detailed computation [1].

Furthermore, analysis of proteins like Bovine Pancreatic Trypsin Inhibitor (BPTI) reveals that changes in correlation entropy can either balance or reinforce changes in first-order entropy, and that main-chain torsions are significant contributors to changes in protein configurational entropy [26]. This underscores the importance of capturing correlations for a correct thermodynamic picture.

Table 2: Sample Uncoupled Internal Entropy Changes Upon Protein Complex Formation [1]

Protein / Binding Partner	PDB Code of Complex	Uncoupled Entropy Change (-TΔS₁𝒟) (kJ mol⁻¹)
Tsg101 protein	1S1Q	190.0
Ubiquitin	1S1Q	248.3
gGGA3 Gat domain	1YD8	44.0
Ubiquitin	1YD8	420.4
Subtilisin Carlsberg	1R0R	527.4
Ovomucoid	1R0R	106.6
Uracil–DNA glycosylase	1UGH	-65.7

Experimental and Computational Protocols

Workflow for Configurational Entropy Calculation

The following diagram illustrates the standard computational workflow for applying MIE/MIST to calculate the configurational entropy change of a binding process.

Detailed Methodology for Host-Guest Binding Analysis

The protocol below, adapted from a study on a host-guest system, provides a detailed template for calculating binding entropy changes [26].

• System Preparation: For the binding of host (A) and guest (B) to form complex (AB), model the molecules with appropriate protonation states and force fields (e.g., GAFF/AM1-BCC). Solvate the systems in a suitable box of solvent molecules (e.g., chloroform or water) and add necessary counter-ions to achieve neutrality.

• Molecular Dynamics (MD) Simulation:

  • Simulation Engine: Use a package like AMBER, GROMACS, or NAMD.
  • Equilibration: First, minimize the system's energy. Then, gradually heat it to the target temperature (e.g., 300 K) under constant volume (NVT) conditions, followed by equilibration under constant pressure (NPT, e.g., 1 atm).
  • Production Run: Perform multiple, long, independent production simulations (microsecond to millisecond scale, depending on system size) in the NPT ensemble to ensure adequate sampling of conformational space. Save trajectory frames at regular intervals (e.g., every 1-100 ps).

• Trajectory Analysis and Feature Selection:

  • For the Unbound Host (A): Extract the time series of all soft internal degrees of freedom (e.g., 8 key torsional angles) from the trajectory. Stiff degrees of freedom (bonds, angles) can be ignored as their entropy change is minimal.
  • For the Bound Complex (AB): Extract the same soft torsions of the host plus the 6 degrees of freedom defining the relative position and orientation of the guest relative to the host.

• Entropy Calculation via MIST/MIE:

  • Probability Density Estimation: From the trajectory data, estimate the 1D and 2D marginal probability distributions ( p(qi) ) and ( p(qi, q_j) ) for all selected degrees of freedom. Kernel Density Estimation (KDE) or histogramming can be used.
  • Compute Entropy Components: Calculate the first-order entropy terms, ( S(Xi) = -kB \langle \ln p(qi) \rangle ), and the pairwise mutual information terms, ( I(Xi;X_j) ), for all variable pairs.
  • Apply MIST: Identify the maximum information spanning tree from the matrix of pairwise mutual information values. Compute the total entropy for each state (free host and complex) using the MIST approximation formula.
  • Calculate Binding Entropy Change: The change in configurational entropy on binding is given by:
    where the ( -k_B \ln(8\pi^2/C^\circ) ) term accounts for the loss of translational and rotational entropy upon forming the complex from the free guest, and ( C^\circ ) is the standard concentration [26].

The Scientist's Toolkit: Essential Research Reagents and Computational Solutions

Table 3: Key Software, Tools, and Their Functions in MIE/MIST Analysis

Tool / Reagent	Type	Primary Function in Analysis
AMBER, GROMACS, NAMD	MD Simulation Software	Generates the classical molecular dynamics trajectories from which conformational distributions are sampled.
Maximum Information Spanning Tree (MIST) Algorithm	Computational Algorithm	Approximates the total configurational entropy by selecting the tree of strongest pairwise correlations.
Mutual Information Expansion (MIE)	Mathematical Framework	Provides the theoretical basis for decomposing total entropy into contributions from individual degrees of freedom and their correlations.
Kernel Density Estimation (KDE)	Statistical Method	Non-parametrically estimates the continuous probability distributions of conformational variables from discrete trajectory data.
Bond-Angle-Torsion (BAT) Coordinates	Internal Coordinate System	Defines the molecular conformation; the Jacobian of the transformation to these coordinates is required for entropy calculations [1].
Generalized AMBER Force Field (GAFF)	Molecular Force Field	Defines the potential energy function, including bond, angle, torsion, and nonbonded interaction parameters, for the MD simulation [26].
JTP-117968	JTP-117968, MF:C31H31F3N2O2, MW:520.6 g/mol	Chemical Reagent
Rapamycin-13C,d3	Rapamycin-13C,d3, MF:C51H79NO13, MW:918.2 g/mol	Chemical Reagent

Applications in Intermolecular Interactions and Drug Discovery

The application of MIE and MIST has profoundly impacted the understanding of intermolecular interactions, especially in structure-based drug design.

• Quantifying Entropy in Protein Binding: These frameworks allow for a complete dissection of the entropy change upon protein-protein or protein-ligand binding. Studies on diverse protein complexes show that coupling terms between internal and external degrees of freedom are significant and that the total configurational entropy change can be approximated by rescaling the sum of uncoupled internal contributions [1]. This finding provides theoretical support for NMR-based methods that estimate entropy changes from order parameters.

• Overcoming Enthalpy-Entropy Compensation: A major challenge in drug design is enthalpy-entropy compensation, where optimizing favorable enthalpy (e.g., stronger hydrogen bonds) often leads to a compensating loss of entropy (reduced flexibility). By providing a detailed, residue-level map of entropy changes, MIE/MIST analyses offer deeper insight into the basic physical principles governing this balance, enabling more rational design of high-affinity ligands [1].

• Informing NMR Data Interpretation: NMR relaxation measurements provide insights into molecular dynamics, often interpreted in terms of entropy. MIE/MIST analyses have demonstrated that changes in correlation are important determinants of entropy changes in biologically relevant processes [26]. This indicates that interpreting NMR data without considering correlation effects could lead to incomplete or misleading conclusions.

Mutual Information Expansion and the Maximum Information Spanning Tree algorithm represent a powerful paradigm shift in how researchers quantify and deconstruct configurational entropy. By moving beyond simplistic, uncoupled models, these frameworks reveal the intricate and significant roles that correlations among molecular degrees of freedom play in driving the thermodynamics of intermolecular interactions. As computational power continues to grow and these methods become more integrated with machine learning techniques, their role in revolutionizing rational drug design and our fundamental understanding of biomolecular function is poised to expand dramatically, enabling the more efficient and accurate discovery of novel therapeutic candidates [28].

The k-th Nearest Neighbor (kNN) method stands as one of the most fundamental and intuitively appealing algorithms in machine learning, with applications spanning economic forecasting, disease diagnosis, and materials science [29] [30]. Its foundational premise is elegant in its simplicity: similar data points tend to reside near one another within the feature space. However, as scientific inquiry increasingly ventures into high-dimensional domains—from genomics with thousands of gene expressions to materials science exploring complex compositional spaces—this foundational algorithm confronts profound challenges collectively known as the "curse of dimensionality" [31]. In high-dimensional spaces, conventional distance metrics like Euclidean distance become less meaningful as the contrast between nearest and farthest neighbors diminishes significantly, thereby diluting the discriminative power essential for kNN's operation [29] [31].

Compounding this issue is kNN's nature as a "lazy learner," which stores all training data and performs predictions at runtime by scanning this entire dataset. This approach results in substantial computational costs, particularly for large-scale datasets common in contemporary research [32]. Furthermore, high-dimensional data frequently contains numerous non-informative or noisy features that can mislead traditional distance calculations and degrade classification performance [29]. These challenges become especially pertinent in molecular research, where accurately quantifying configurational entropy—a critical determinant of free energies in processes like protein-folding, noncovalent association, and conformational change—demands sophisticated analytical approaches capable of capturing complex, many-body correlations in high-dimensional spaces [33].

This technical guide provides a comprehensive examination of advanced kNN methodologies specifically engineered to overcome these dimensional barriers, with particular emphasis on their applicability to research concerning configurational entropy and intermolecular interactions. By synthesizing cutting-edge algorithmic innovations with practical implementation frameworks, we aim to equip researchers with the tools necessary to harness kNN's potential even in the most challenging high-dimensional research contexts.

Algorithmic Innovations for High-Dimensional Spaces

Space Partitioning and Indexing Strategies

Traditional space partitioning structures like k-d trees and ball-trees have demonstrated effectiveness in organizing data for efficient neighbor searches in low-dimensional settings. However, their performance substantially degrades as dimensionality increases because most of the search space must be explored needlessly [34]. This limitation has spurred the development of more sophisticated indexing methodologies tailored for high-dimensional environments.

Telescope Indexing (tik-NN) represents a significant advancement by employing a sequence of indices that progressively refine the search space. This approach partitions data into groups of points similarly distanced from a reference point within a B+ tree structure, effectively limiting the search scope for any kNN query. The methodology establishes that this limited search space can be efficiently explored by any indexing techniques applicable to the entire dataset. Empirical evaluations demonstrate that tik-NN achieves notable speedup compared to naive, k-d tree, and ball-tree based kNN approaches, along with other state-of-the-art approximate kNN search methods in high-dimensional data [34].

Table 1: Comparative Analysis of Space Partitioning Methods for kNN

Method	Core Mechanism	Dimensionality Strength	Key Limitations
k-d Tree [31]	Binary partitioning using hyperplanes perpendicular to coordinate axes	Low-dimensional spaces (< 20 dimensions)	Performance degrades rapidly with increasing dimensions; suffers from curse of dimensionality
Ball-tree [31]	Hypersphere-based partitioning using triangle inequality for pruning	Moderate-dimensional spaces	Query performance highly dependent on data structure; affected by curse of dimensionality
Telescope Indexing (tik-NN) [34]	B+ tree structure grouping points by distance to reference points	High-dimensional spaces	Requires determination of optimal number of partitions and reference points
VP-tree & MVP-tree [31]	Distance-based partitioning using vantage points	High-dimensional spaces	Performance depends on selection of effective vantage points

Clustering-Based Approaches

Clustering methodologies offer a powerful alternative to traditional space partitioning by grouping similar data trajectories before performing nearest neighbor searches. The Clustering-based KNN Regression for Longitudinal Data (CKNNRLD) algorithm exemplifies this approach by first clustering data using the K-means for longitudinal data (KML) algorithm, then searching for nearest neighbors within the relevant cluster rather than across the entire dataset [32].

This strategy demonstrates particular efficacy for longitudinal studies requiring flexible methodologies for predicting response trajectories based on time-dependent and time-independent covariates. According to simulation findings, CKNNRLD implementation "took less time compared to using the KNN implementation (for N > 100)" and "predicted the longitudinal responses more accurately and precisely than the equivalent algorithm" [32]. In specific scenarios with N = 2000, T = 5, D = 2, C = 4, E = 1, and R = 1, CKNNRLD execution time was approximately 3.7 times faster than typical KNN execution time [32].

The fundamental advantage of clustering-based approaches lies in their ability to reduce the computational burden by structuring the search space. Since the KNN method "needs all of the training data to identify the nearest neighbors, it tends to operate slowly as the number of individuals in longitudinal research increases (for N > 500)" [32]. By restricting searches to relevant clusters, CKNNRLD and similar algorithms significantly enhance computational efficiency while maintaining, and often improving, prediction accuracy.

Feature Sampling and Ensemble Methods

The presence of numerous noisy or non-informative features in high-dimensional data presents a substantial challenge for kNN classification, as these features dilute and potentially mislead correct information [29]. Random k Conditional Nearest Neighbor (RkCNN) addresses this limitation by aggregating multiple kCNN classifiers, each constructed from a randomly sampled feature subset [29].

The RkCNN algorithm operates through a sophisticated workflow:

• Generate multiple random feature subsets from the complete feature space
• Calculate a separation score (BV/WV) for each subset to quantify its informativeness
• Sort feature subsets by their separation scores in descending order
• Construct kCNN models on the top-performing subsets
• Compute weights for each classifier based on relative separation scores
• Aggregate class probability estimates using weighted averaging

This approach incorporates a critical quality control mechanism by disregarding results from feature subset spaces with relatively low separation scores, thus minimizing the incorporation of noisy information. The method has demonstrated particular promise in gene expression datasets, where the curse of dimensionality frequently renders distance-based information less effective [29].

Distance Metric Innovations

Conventional distance metrics like Euclidean distance often become less discriminative in high-dimensional spaces. In response, researchers have developed specialized distance measures to enhance kNN's performance in challenging dimensional environments. The Hassanat distance metric has demonstrated particular efficacy, achieving the highest average accuracy (83.62%) in comparative studies of KNN variants for disease prediction, followed by ensemble approach KNN (82.34%) [30].

The fundamental advantage of Hassanat distance lies in its ability to maintain discriminative power even when features exhibit different scales or distributions—a common scenario in high-dimensional scientific data. Similarly, generalized mean distance calculations and vector creations for the nearest neighbors of each different class have shown promise in addressing the limitations of unbiased weight attributions and enhancing accuracy through local mean vector calculations [30].

Table 2: Advanced kNN Variants for High-Dimensional Spaces

Variant	Core Innovation	Performance Advantage	Applicable Domains
CKNNRLD [32]	Clustering of longitudinal data before neighbor search	3.7x faster execution for N=2000; improved prediction accuracy	Longitudinal medical studies, spirometry data, repeated measures
RkCNN [29]	Ensemble of kCNN classifiers on random feature subsets	Improved classification performance on gene expression data	Genomics, high-dimensional biological data
tik-NN [34]	Telescope indexing with B+ tree structure	Significant speedup over tree-based approaches in high dimensions	Large-scale high-dimensional datasets
Hassanat KNN [30]	Novel distance metric maintaining discriminative power	83.62% average accuracy across disease datasets	Medical diagnosis, pattern recognition
Fuzzy KNN [30]	Membership assignment and fuzzy sets	Handles uncertainty in class boundaries	Noisy data, overlapping classes

Methodological Protocols for kNN in Entropy Research

Configurational Entropy Estimation Using Nearest-Neighbor Methods

The estimation of configurational entropy represents a longstanding computational challenge in molecular research, with traditional approaches like the quasi-harmonic approximation often proving inadequate when probability distributions deviate significantly from Gaussian assumptions, particularly in multimodal systems [33]. The nearest-neighbor (NN) method of entropy estimation, introduced by Hnizdo et al., provides a powerful nonparametric alternative that utilizes k-th nearest neighbor estimators of entropy [33].

These estimators possess crucial mathematical properties: they are asymptotically unbiased and asymptotically consistent (exhibiting asymptotically vanishing variance), ensuring accuracy for any probability distribution given sufficient molecular simulation data and computational resources [33]. The NN method excels in its efficient utilization of available simulation data, enabling accurate entropy estimations for fairly high-dimensional systems. However, it nevertheless confronts the "curse of dimensionality," as convergence and computational complexity eventually become intractable with increasing dimensionality [33].

The Mutual Information Expansion (MIE) framework offers a systematic approach to addressing this dimensional challenge by expanding the entropy of a multidimensional system in mutual information terms of increasing order m that capture m-body correlations among molecular coordinates [33]. A truncation of the MIE provides a well-characterized approximation to the full joint entropy that includes correlations up to a specified order. The combination of the systematic dimension-reduction approximations of MIE with the power of the NN method creates a synergistic approach that delivers both computational efficiency and estimation accuracy [33].

Experimental Protocol: kNN for Molecular Entropy Calculation

Objective: To compute the configurational entropy of internal rotation for a molecule with multiple dihedral degrees of freedom (e.g., the R,S stereoisomer of tartaric acid with 7 internal-rotation degrees of freedom) using the combined MIE and nearest-neighbor approach.

Materials and Data Requirements:

• Molecular dynamics simulation trajectories sampling all relevant dihedral angles
• Sufficient sampling to achieve convergence (typically 10^5-10^7 frames depending on system complexity)
• Computational resources for distance calculations between high-dimensional configurations

Step-by-Step Procedure:

• Data Preparation:

  • Extract all dihedral angles from molecular dynamics trajectories
  • Format data as an n × d matrix, where n is the number of observations and d is the number of dihedral degrees of freedom
  • Apply periodic boundary conditions to ensure angular continuity

• Mutual Information Expansion Setup:

  • Define the full joint system S(1,...,s) representing all dihedral angles
  • Compute lower-dimensional marginal entropies S(i), S(i,j), S(i,j,k) for all combinations
  • Calculate mutual information terms using the relationship: I(i,j) = S(i) + S(j) - S(i,j)

• Nearest-Neighbor Entropy Estimation:

  • For each entropy term in the MIE, implement the k-th nearest neighbor estimator
  • Select an appropriate k value (typically k=3-5) to balance bias and variance
  • Compute the entropy using the NN estimator formula for each subsystem

• MIE Truncation and Final Calculation:

  • Assemble MIE terms according to the expansion: S(1,...,s) = Σ(-1)^(m+1) * T_m(1,...,s)
  • Evaluate convergence with increasing expansion order
  • Truncate at the optimal order (typically 2nd or 3rd order) based on computational constraints and accuracy requirements

Validation and Quality Control:

• Compare results with alternative methods when available
• Assess sampling adequacy through block averaging or bootstrap resampling
• Verify internal consistency through redundancy analysis in mutual information terms

This protocol leverages the strengths of both MIE and NN methods: the systematic dimension-reduction approximation of MIE and the nonparametric, adaptive binning of the NN approach, which proves particularly valuable for higher-order correlations where data sparsity challenges histogram-based methods [33].

Performance Analysis and Comparative Evaluation

Quantitative Assessment of kNN Variants

Rigorous performance evaluation is essential for selecting appropriate kNN methodologies for high-dimensional applications. Comprehensive benchmarking across diverse datasets reveals distinct performance characteristics among advanced kNN variants.

Table 3: Performance Comparison of kNN Variants Across Multiple Domains

Algorithm	Accuracy (%)	Precision	Recall	Computational Efficiency	Dimensional Robustness
Classic KNN [30]	64.22-76.84	Moderate	Moderate	Low	Poor
Hassanat KNN [30]	83.62	High	High	Moderate	Good
Ensemble KNN [30]	82.34	High	High	Moderate	Good
CKNNRLD [32]	N/A (Regression)	N/A	N/A	High (3.7x speedup)	Excellent for longitudinal data
RkCNN [29]	High (Gene data)	High	High	Moderate	Excellent
Fuzzy KNN [30]	75.91	Moderate-High	Moderate-High	Moderate	Good

The performance differentials observed across these variants underscore the importance of selecting algorithms tailored to specific data characteristics and research objectives. For instance, while Hassanat KNN demonstrates superior overall accuracy in disease prediction contexts, CKNNRLD offers exceptional computational efficiency for longitudinal studies where temporal correlations are present [32] [30].

Case Study: kNN in High-Dimensional Alloy Design

The application of kNN methodologies to high-dimensional materials science problems illustrates their utility in complex research domains. In multi-principal element alloys (MPEAs), researchers confront the challenge of visualizing and optimizing composition-property relationships in high-dimensional design spaces where conventional approaches fail [35].

Advanced visualization techniques like the Uniform Manifold Approximation and Projection (UMAP) have been employed to project entire barycentric design spaces to 2D, enabling researchers to intuitively comprehend chemistry-property relationships that would otherwise remain opaque in high-dimensional space [35]. These projected spaces can then inform kNN-based classification and regression tasks, facilitating alloy discovery and optimization.

The synergy between dimensionality reduction techniques like UMAP and enhanced kNN algorithms creates a powerful framework for navigating complex design spaces. This approach demonstrates how kNN methodologies can integrate into broader research pipelines to overcome dimensional barriers in scientific exploration.

The Scientist's Toolkit: Essential Research Reagents

Table 4: Essential Computational Tools for High-Dimensional kNN Research

Tool/Algorithm	Function	Application Context
Longitudinal k-means (KML) [32]	Clustering of trajectory data	Preprocessing step for CKNNRLD in longitudinal studies
Mutual Information Expansion [33]	Systematic entropy approximation	Configurational entropy calculation from molecular simulations
Hassanat Distance Metric [30]	Enhanced similarity measurement	kNN classification with improved discriminative power
UMAP Projection [35]	Dimensionality reduction	Visualization and analysis of high-dimensional design spaces
Separation Score (BV/WV) [29]	Feature subset quality assessment	Classifier weighting in RkCNN ensemble methods
k-th NN Entropy Estimator [33]	Nonparametric entropy estimation	Configurational entropy from limited molecular simulation data
AL-438	AL-438, MF:C23H25NO2, MW:347.4 g/mol	Chemical Reagent
VUF14862	VUF14862, MF:C26H32N4O2, MW:432.6 g/mol	Chemical Reagent

The k-th Nearest Neighbor method continues to evolve as an indispensable tool for high-dimensional data analysis in scientific research, particularly in domains requiring precise quantification of configurational entropy for understanding intermolecular interactions. Through strategic innovations in space partitioning, clustering, ensemble methods, and distance metrics, researchers have substantially mitigated the curse of dimensionality that traditionally limited kNN's applicability in high-dimensional spaces.

The integration of mutual information expansion with nearest-neighbor entropy estimation represents a particularly promising direction for molecular research, enabling accurate quantification of configurational entropy even for complex, multimodal distributions [33]. Similarly, specialized kNN variants like CKNNRLD offer robust solutions for longitudinal data analysis, achieving both improved accuracy and substantial computational efficiency gains [32].

As scientific data continues to increase in both dimensionality and volume, further innovation in kNN methodologies will be essential. Promising research directions include the development of hybrid approaches combining kNN with deep learning architectures, adaptive algorithms that dynamically optimize their parameters based on data characteristics, and enhanced implementations leveraging parallel and distributed computing frameworks. Through continued methodological refinement, kNN will maintain its position as a cornerstone algorithm for extracting meaningful insights from the high-dimensional data that increasingly defines the frontiers of scientific discovery.

Configurational entropy is a central, yet historically underexplored, component of the Gibbs free energy change in noncovalent biomolecular interactions, including protein folding, protein-ligand binding, and self-assembly processes [1] [36]. Its quantification is crucial for a fundamental understanding of biological processes and for applied contexts like computational drug design, where it can help overcome the challenge of enthalpy-entropy compensation [1]. Configurational entropy originates from the solute degrees of freedom and represents the entropy change associated with the reduction of available configurations upon binding or folding [36]. Contrary to the traditional assumption that its contribution is negligible, recent experimental evidence demonstrates that it can be of a magnitude similar to the solvent entropy contribution, thus exerting a strong influence on the overall thermodynamics of interactions [1]. This whitepaper details the calorimetric methods, primarily Isothermal Titration Calorimetry (ITC), used to experimentally determine these critical configurational thermodynamic values.

Theoretical Foundations

Defining Configurational Thermodynamic Values

In the context of binding interactions, the overall change in Gibbs free energy ((ΔG)) is described by the fundamental equation: [ ΔG = ΔH - TΔS ] where (ΔH) is the change in enthalpy, (T) is the temperature, and (ΔS) is the change in total entropy [37].

The total entropy change ((ΔS)) can be conceptually partitioned into contributions from the solvent and the solute: [ ΔS = ΔS{solvent} + ΔS{solute} ] The solute entropy, (ΔS{solute}), is often equated with the configurational entropy, (ΔS{conf}), which stems from the restriction of translational, rotational, and internal degrees of freedom of the biomolecules upon forming a complex [1].

When comparing the amorphous and crystalline states of a drug substance, configurational properties represent the difference between the two states [4]: [ G{conf} = H{conf} - T S{conf} ] Here, (H{conf}) is the configurational enthalpy and (S{conf}) is the configurational entropy, defined as: [ H{conf}(T) = H{amorph}(T) - H{crystal}(T) ] [ S{conf}(T) = S{amorph}(T) - S_{crystal}(T) ] These values indicate the thermodynamic driving force for recrystallization and the associated solubility advantage of the amorphous form [4].

The Link Between Calorimetry and Configurational Entropy

Calorimetry, particularly ITC, measures the heat released or absorbed during a binding event, providing a direct experimental measurement of the enthalpy change, (ΔH) [37] [38]. In a single experiment, ITC can determine the binding affinity ((KA) or (KD)), stoichiometry ((n)), and enthalpy ((ΔH)) [37]. Once (ΔG) is derived from the binding affinity ((ΔG = -RT \ln K_A)) and (ΔH) is measured directly, the entropic component (TΔS) is resolved using the Gibbs free energy equation: [ TΔS = ΔH - ΔG ] This resolved entropy value includes the coveted configurational entropy change, albeit convolved with solvent and other effects [37] [38].

Experimental Methodologies

Core Principle of Isothermal Titration Calorimetry (ITC)

ITC operates by maintaining two cells—a sample cell and a reference cell—at an identical and constant temperature [39] [37]. The reference cell typically contains water or buffer, while the sample cell contains one of the binding partners (e.g., a protein). The other binding partner (e.g., a ligand) is titrated into the sample cell in a series of injections.

If binding occurs, heat is either absorbed or released, creating a temperature difference between the two cells. The instrument's feedback system applies power to a heater to compensate for this difference and return the cells to the same temperature. The primary observable is the difference in power ((ΔP)) required to maintain thermal equilibrium between the reference and sample cells, which is equal to the rate of energy released by the binding reaction (( \dot{E}_{REL} )) [39]. Integrating this power signal over time for each injection yields the total heat effect for that injection [37].

Detailed ITC Experimental Protocol

A robust ITC experiment requires careful planning and execution, as outlined below and summarized in Table 1.

1. Buffer Matching: The two binding partners must be in identical buffers to minimize heats of dilution that can obscure the heats of binding. Even small differences in pH, or the use of additives like DMSO or reducing agents, can cause significant background heats [37].

2. Sample Preparation:

• Concentration: Accurate determination of molar concentration is critical. Errors in the cell concentration affect stoichiometry, while errors in the syringe concentration directly translate to errors in the measured (K_D) and (ΔH) [37].
• Purity and Homogeneity: Protein aggregates can severely interfere with ITC data. Samples should be centrifuged or filtered before loading. Assessment of protein heterogeneity via light scattering or purification by size-exclusion chromatography is recommended [37].

3. Experimental Setup:

• The c-value (( c = n \cdot [M]{cell} / KD )) is a key parameter for experimental design. Ideally, the c-value should be between 10 and 100. This ensures the binding isotherm has a well-defined sigmoidal shape, allowing for accurate fitting of all parameters ((K_D), (n), (ΔH)) [37].
• Typical starting concentrations involve a 10- to 20-fold higher concentration of ligand in the syringe compared to the macromolecule in the cell [37].

4. Data Analysis: The integrated heat data from the titration is fitted to a suitable binding model (e.g., a single-site model). The nonlinear regression analysis directly yields the binding constant ((KA = 1/KD)), stoichiometry ((n)), and enthalpy ((ΔH)). The Gibbs free energy and entropy are then calculated as: [ ΔG = -RT \ln K_A ] [ ΔS = (ΔH - ΔG)/T ]

Table 1: Key Steps in an ITC Experiment

Step	Key Action	Purpose & Rationale
1. Buffer Preparation	Dialyze both molecules into the identical buffer.	To minimize heats of dilution that mask the binding signal.
2. Sample Loading	Load protein into cell (~300 µL); load ligand into syringe (~100-120 µL).	To ensure sufficient material for the experiment and complete cell filling.
3. c-value Optimization	Estimate (KD); adjust cell/syringe concentrations so that ( c = n \cdot [M]{cell} / K_D ) is 10-100.	To achieve a binding isotherm that allows accurate fitting of (K_D), (n), and (ΔH).
4. Titration	Perform a series of controlled injections of ligand into protein.	To measure the heat associated with binding as the binding sites are progressively filled.
5. Data Fitting	Fit integrated heat data to a binding model.	To extract the thermodynamic parameters (K_A), (n), and (ΔH).
6. Entropy Calculation	Calculate (ΔG) from (K_A), then (TΔS) from (ΔG) and (ΔH).	To resolve the entropic contribution, which includes configurational entropy.

The following workflow diagram illustrates the complete experimental and analytical process for an ITC experiment.

The Scientist's Toolkit: Essential Reagents and Materials

Table 2: Essential Research Reagents and Materials for ITC

Item	Function & Application
High-Purity Macromolecule	The protein or other large molecule whose binding is under study. Accurate concentration and the absence of aggregates are critical for reliable data.
High-Purity Ligand	The small molecule, drug candidate, or other binding partner titrated into the macromolecule. Must be in the exact same buffer as the macromolecule.
Perfectly Matched Buffer	The solvent for both binding partners. Serves as the chemical background; mismatches are a primary source of experimental error and heat artifacts.
Degassing Unit	Used to remove dissolved gases from samples and buffers. Prevents the formation of air bubbles in the calorimeter cells, which can cause erratic baseline drift.
Reducing Agents (e.g., TCEP)	Used to stabilize proteins by preventing disulfide bond formation. Should be kept at low concentrations (e.g., ≤ 1 mM) as they can cause baseline artifacts.
SJF-1521	SJF-1521, MF:C57H61ClFN7O9S, MW:1074.7 g/mol
ASN02563583	ASN02563583, MF:C25H24N4O3S, MW:460.5 g/mol

Data Interpretation and Advanced Analysis

Extracting and Interpreting Configurational Entropy

The entropy value (TΔS) obtained from an ITC experiment is a composite parameter. For a more nuanced interpretation, especially regarding configurational entropy, advanced analysis and complementary methods are required.

Entropy–Enthalpy Compensation: A common observation in biomolecular interactions is that favorable binding enthalpy ((ΔH < 0)) is often offset by unfavorable binding entropy ((TΔS < 0)), and vice versa. This phenomenon, known as entropy-enthalpy compensation, complicates drug optimization efforts [1]. A deep understanding of configurational entropy can help dissect this compensation. For instance, a highly rigid, pre-organized ligand might bind with a favorable enthalpy but a large unfavorable configurational entropy change due to its lack of flexibility. Conversely, a flexible ligand might pay a small configurational entropy penalty but also achieve less favorable enthalpic interactions.

Complementary Methods: Computational approaches, particularly molecular dynamics (MD) simulations coupled with methods like the mutual information expansion (MIE) or maximum information spanning tree (MIST), can decompose the total configurational entropy into contributions from internal (vibrational, torsional) and external (rotational, translational) degrees of freedom, as well as their coupling terms [1]. These studies show that different coupling terms can contribute significantly to the overall configurational entropy change, contrary to common simplifying assumptions [1]. Furthermore, combining ITC with other biophysical techniques like Thermal Diffusion Forced Rayleigh Scattering (TDFRS) can provide insights into changes in hydration layers—another significant source of entropy change upon binding [38].

Table 3: Thermodynamic Parameters from a Model ITC Experiment (Protein-Ligand Binding)

Parameter	Symbol	Value	Units	Interpretation
Dissociation Constant	(K_D)	0.1	µM	High binding affinity.
Gibbs Free Energy	(ΔG)	-40.5	kJ/mol	Binding is spontaneous.
Enthalpy	(ΔH)	-60.0	kJ/mol	Exothermic binding; suggests strong interactions (H-bonds, van der Waals).
Entropy	(TΔS)	-19.5	kJ/mol	Unfavorable; suggests a loss of flexibility/degrees of freedom (configurational entropy) and/or hydrophobic effects.

Calorimetric methods, with ITC at the forefront, provide an indispensable, label-free route for determining the full suite of thermodynamic parameters governing biomolecular interactions. By directly measuring binding enthalpy, ITC allows for the calculation of the entropic contribution, which contains the critical, albeit complex, signature of configurational entropy. A rigorous experimental approach, encompassing meticulous sample preparation and optimal instrument setup, is paramount for obtaining high-quality data. The interpretation of this data is vastly enriched when ITC is viewed not as a standalone technique, but as a central component of an integrated strategy that includes computational entropy decomposition and other biophysical methods. This combined approach is key to unlocking a deeper understanding of the role of configurational entropy in intermolecular interactions, thereby accelerating rational drug design and broadening our fundamental knowledge of biological processes.

Within the broader thesis on the role of configurational entropy in intermolecular interactions research, the integration of computational and experimental methods emerges as a paramount strategy for robust quantitative estimation. The central problem in modeling complex molecules, such as liquid crystals and biological macromolecules, is understanding the precise relationship between molecular structure and material properties or functions [40]. Configurational entropy, a key constituent of the free energy in noncovalent biomolecular interactions, remains notoriously difficult to measure experimentally or calculate from atomistic simulations, yet it can be of similar magnitude to solvent entropy and thus critically impact thermodynamics [1]. Recent advances in integrative structural biology demonstrate that combining biophysical experimental data with computational modeling can assist and enrich the interpretation of results, providing new detailed molecular understanding of dynamic systems that change conformation, bind partners, and perform reactions [41]. This in-depth technical guide outlines the core strategies, methodologies, and practical tools for effectively combining these approaches to gain unprecedented insights into molecular mechanisms, with a particular emphasis on estimating configurational entropy and its contribution to intermolecular interactions.

Core Strategic Approaches for Integration

The combination of experimental and computational methods can be implemented through several distinct strategic paradigms. The choice of strategy depends on the specific research question, the nature of the available experimental data, and the computational resources at hand.

The following table summarizes the four major strategies for integrating computational and experimental data:

Table 1: Core Strategies for Integrating Computational and Experimental Data

Strategy	Brief Description	Key Advantages	Common Software/Tools
Independent Approach	Experimental and computational protocols are performed independently, and their results are compared post-hoc [41].	Can reveal "unexpected" conformations; provides plausible physical pathways [41].	Molecular dynamics (MD) suites (GROMACS [41], CHARMM [41]), Monte Carlo (MC) simulations [41].
Guided Simulation (Restrained) Approach	Experimental data are incorporated as restraints to guide the conformational sampling during the simulation [41].	More efficient sampling of experimentally relevant conformations [41].	GROMACS [41], CHARMM [41], Xplor-NIH [41], Phaistos [41].
Search and Select (Reweighting) Approach	A large pool of conformations is generated computationally, then experimental data are used to select a sub-ensemble that fits the data [41].	Simplifies integration of multiple data types; initial pool can be re-used for new data [41].	ENSEMBLE [41], BME [41], MESMER [41], Flexible-meccano [41].
Guided Docking	Experimental data are used to define binding sites and guide the prediction of complex structures [41].	Ideal for studying biomolecular complexes and interactions [41].	HADDOCK [41], IDOCK [41], pyDockSAXS [41].

The Critical Role of Configurational Entropy

In the context of these integrative strategies, accurately capturing configurational entropy change (ΔS_conf) is a significant challenge and a key objective. This entropy stems from the solute degrees of freedom only and is a central component of the Gibbs free energy change (ΔG) in noncovalent binding processes, which governs the likelihood of interactions occurring [1]. The configurational entropy can be decomposed into contributions from molecular internal degrees of freedom (vibrations, rotations) and external, rigid body roto-translational degrees of freedom, along with often-ignored coupling terms between them [1]. The analytical framework for this decomposition relies on the mutual information expansion (MIE) and related maximum information spanning tree (MIST) approximations, which allow for a comprehensive numerical analysis of the individual contributions to the total entropy change upon binding [1]. Understanding these components is vital, as the flexibility of alkyl chains in molecules, for instance, can be regarded as a source of entropy to tune the delicate balance and stability of mesophases in liquid crystals [40].

Detailed Experimental and Computational Methodologies

This section provides detailed protocols for key experiments and the computational procedures used to integrate their data.

Key Experimental Techniques and Data Integration Protocols

Quantitative data from various biophysical techniques serve as critical inputs for computational integration. The following table outlines common techniques, their measurable variables, and how the data are incorporated into computational models.

Table 2: Key Experimental Techniques and Their Integration into Computational Models

Experimental Technique	Measured Biochemical/Biophysical Variables	Data Integration Method & Restraint Type
Nuclear Magnetic Resonance (NMR)	Distance restraints (e.g., from NOEs), chemical shifts, scalar couplings, residual dipolar couplings (RDCs) [41].	Used as distance/angle restraints in guided simulations or for filtering/selecting conformations in search-and-select approaches [41].
X-ray Crystallography	Electron density maps, dispersion patterns [41].	Used to compute a structural model compatible with the data via computational protocols [41]. Often a starting point for simulations.
Small-Angle X-ray Scattering (SAXS)	Low-resolution particle shape and size (pair distribution function) [41].	Can be incorporated into docking (e.g., pyDockSAXS [41]) or used to select ensembles that match the experimental scattering profile.
Single-Molecule Fluorescence / FRET	Distances and distance distributions between dye pairs, dynamics on micro- to millisecond timescales.	Distance distributions can be used as restraints in guided MD or to reweight conformational ensembles.
Isothermal Titration Calorimetry (ITC)	Binding affinity (K_d), enthalpy change (ΔH), stoichiometry (n).	The measured ΔG and ΔH can be used to calculate the experimental TΔS, providing a target for validating computed free energies and entropy contributions [1].

Computational Protocols for Entropy Estimation and Integration

Protocol 1: Guided Molecular Dynamics Simulation with Experimental Restraints

• System Setup: Obtain an initial atomic structure of the molecule or complex, often from crystallography or NMR. Solvate the structure in a water box, add necessary ions to neutralize the system, and define the force field parameters.
• Restraint Preparation: Convert the experimental data (see Table 2) into a mathematical form usable as an external potential. For example, NMR NOE-derived distances are often implemented as harmonic distance restraints.
• Energy Minimization: Perform an initial energy minimization to remove any steric clashes in the initial structure.
• Equilibration: Run short MD simulations in the NVT and NPT ensembles to equilibrate the temperature and density of the system.
• Production Run with Restraints: Execute a production MD simulation with the experimental restraints active. The total potential energy of the system now includes the force field terms plus the additional restraint energy terms, which guide the conformation to be consistent with the data [41].
• Analysis: Analyze the resulting trajectory to extract the ensemble of structures, dynamic properties, and other quantities of interest.

Protocol 2: Configurational Entropy Calculation using Mutual Information Expansion (MIE)

• Trajectory Generation: Perform extensive molecular dynamics (MD) simulations of the system (e.g., isolated binding partners and their complex) to sample the conformational space [1].
• Coordinate Transformation: Transform the Cartesian coordinates from the MD trajectory into internal coordinates (Bond-Angle-Torsion, or BAT coordinates) to separate internal and external degrees of freedom [1].
• Entropy Decomposition: Apply the mutual information expansion (MIE) framework to decompose the total configurational entropy into contributions from:
  • Uncorrelated internal degrees of freedom.
  • Uncorrelated external degrees of freedom.
  • Coupling (correlation) terms between internal and external degrees of freedom [1].
• Entropy Change Calculation: Calculate the entropy change upon binding (ΔSconf) as the difference between the configurational entropy of the complex and the sum of the entropies of the isolated partners. Rescaling the sum of uncoupled contributions from internal degrees of freedom can provide a good approximation of the total ΔSconf, supporting NMR-based estimation approaches [1].

Visualizing Workflows and Logical Relationships

The following diagrams, generated with Graphviz, illustrate the logical relationships and workflows described in this guide.

Integrative Analysis Workflow

Configurational Entropy in Binding

The Scientist's Toolkit: Research Reagent Solutions

This section details essential computational and experimental "reagents" required for successful integrative studies.

Table 3: Essential Research Reagents and Tools for Integrative Studies

Category	Item / Software / Resource	Primary Function in Integrative Research
Computational Sampling Engines	GROMACS [41], CHARMM [41], AMBER	Molecular dynamics simulation software for generating conformational ensembles and performing guided simulations with restraints.
Enhanced Sampling Algorithms	Replica Exchange MD (REMD), Metadynamics, Accelerated MD [41]	Computational methods to enhance the sampling of rare conformational events and free energy landscapes.
Ensemble Selection & Reweighting Tools	ENSEMBLE [41], BME [41], MESMER [41]	Programs that select or reweight a pool of conformations to generate an ensemble that best fits experimental data.
Integrative Modeling Platforms	Xplor-NIH [41], Phaistos [41], HADDOCK [41]	Software suites specifically designed to incorporate experimental data as restraints during structure calculation and docking.
Entropy Calculation Frameworks	MIST (Maximum Information Spanning Tree) [1], MIE (Mutual Information Expansion) [1]	Analytical frameworks and their implementations to dissect and calculate configurational entropy from MD trajectories.
Key Experimental Data Sources	NMR Spectrometers, ITC Calorimeters, SAXS Instruments, Mass Spectrometers	Instruments to generate primary experimental data on structure, dynamics, interactions, and thermodynamics for integration.
Adriforant hydrochloride	Adriforant hydrochloride, MF:C13H23ClN6, MW:298.81 g/mol	Chemical Reagent
CZY43	CZY43, MF:C42H53Cl2N5O3, MW:746.8 g/mol	Chemical Reagent

The integrative approach, which synergistically combines computational and experimental data, provides a powerful framework for achieving robust estimation of molecular properties, with a particular emphasis on the challenging quantification of configurational entropy. By moving beyond independent comparisons to guided simulations, search-and-select ensemble methods, and informed docking, researchers can significantly enrich the interpretation of their data. This yields detailed molecular models and a more profound understanding of the mechanisms underpinning intermolecular interactions. As computational power and experimental techniques continue to advance, these integrative strategies are poised to become the cornerstone of rational drug design and the exploration of complex biological processes, ultimately allowing for a more precise dissection of the energetic components, including the critical role of configurational entropy, that govern molecular recognition and function.

Overcoming Practical Challenges: Entropy-Enthalpy Compensation and Desolvation Penalties

Enthalpy-entropy compensation (EEC) is a widely observed phenomenon in thermodynamics where, for a series of related chemical or biological processes, more favorable (more negative) enthalpy changes are counterbalanced by less favorable (more negative) entropy changes, and vice versa. This compensatory behavior results in a relatively smaller variation in the overall Gibbs free energy (ΔG) than would be observed if either enthalpy (ΔH) or entropy (ΔS) acted independently [42]. The relationship is mathematically described by the Gibbs free energy equation: ΔG = ΔH - TΔS, where T is the absolute temperature. For a series of reactions or binding events, a linear relationship between ΔH and ΔS is often observed: ΔH = α + βΔS, where α is the intercept and β is the compensation temperature (Tc) [43] [42].

This compensation effect has profound implications across chemical, physical, and biological sciences. In the context of intermolecular interactions and drug development, understanding EEC is crucial because it influences binding affinity and specificity. The phenomenon is intimately connected to configurational entropy—the measure of disorder associated with the spatial arrangements and fluctuations of molecules [3] [10]. When a ligand binds to its receptor, restrictions in molecular motions lead to a loss of configurational entropy, which must be compensated by favorable enthalpy gains (typically through the formation of non-covalent interactions) to achieve tight binding [3] [44].

This technical guide explores the fundamental principles, computational methodologies, and experimental evidence for EEC, with particular emphasis on its relationship to configurational entropy in biomolecular interactions. We provide researchers and drug development professionals with a comprehensive framework for understanding, quantifying, and applying this ubiquitous trade-off in their work.

Theoretical Foundations

Historical Context and Key Concepts

The compensation effect was first systematically observed by F.H. Constable in 1925 for the catalytic dehydrogenation of primary alcohols [42]. Since then, it has been recognized under various names across different disciplines, including the isokinetic relationship (for kinetic processes) and isoequilibrium relationship (for thermodynamic processes) [42]. In biochemistry, EEC is often invoked to explain the relatively narrow range of binding affinities or folding stabilities observed despite significant variations in experimental conditions or molecular structures [43].

The compensation temperature (Tc) is a crucial parameter in EEC analysis. When the experimental temperature (T) equals Tc, all reactions in the series exhibit the same free energy change (ΔG) or rate constant [42]. This can be visualized as a common intersection point in a van't Hoff plot (for thermodynamics) or an Arrhenius plot (for kinetics) [42].

Statistical Mechanical Perspectives

From a statistical mechanical standpoint, EEC arises from the fundamental relationship between energy level distributions and thermodynamic functions. Preferential population of lower energy states simultaneously decreases both the mean energy (related to enthalpy) and the disorder (entropy) of the system [43]. This intrinsic connection explains why ΔH and ΔS often change in the same direction.

For complex, fluctuating systems like proteins, EEC may reflect the shape of the potential energy surface, the distribution of accessible energy states, or interactions between different system components [43]. However, it is essential to distinguish genuine compensatory behavior from statistical artifacts or constrained experimental conditions that can produce spurious correlations [43].

Relationship to Configurational Entropy

Configurational entropy quantifies the disorder associated with the spatial arrangements and internal degrees of freedom of molecules, including bond rotations, vibrations, and large-scale conformational changes [10]. In protein-ligand binding, significant losses in configurational entropy occur when flexible molecules become restrained upon complex formation [3]. These entropy losses must be offset by favorable enthalpy gains from newly formed molecular interactions, creating the classic EEC pattern [3] [44].

Table 1: Key Entropy Concepts in Biomolecular Interactions

Term	Definition	Role in Binding
Configurational Entropy	Disorder from molecular spatial arrangements and internal degrees of freedom [10]	Decreases upon binding due to restriction of motions [3]
Solvent Entropy	Disorder of water molecules surrounding biomolecules	Often increases upon binding if hydrophobic surfaces are buried
Vibrational Entropy	Disorder from atomic vibrations around equilibrium positions	Can increase or decrease depending on complex stiffness [3]
Mutual Information	Measure of correlation between different molecular motions [3]	Correlated motions can reduce total entropy loss [3]

Computational Methodologies

Molecular Dynamics Simulations

Molecular dynamics (MD) simulations provide atomic-level insights into molecular motions and enable quantification of entropy changes. By numerically solving Newton's equations of motion for all atoms over time, MD simulations generate trajectories that sample the accessible conformational space [10]. For accurate entropy calculations, these simulations must be sufficiently long to capture relevant motions, often requiring microsecond-scale sampling [3].

Mutual Information Expansion (MIE)

The MIE approach offers a systematic framework for computing configurational entropy from MD simulations by accounting for correlations between different degrees of freedom [3] [10]. The second-order MIE approximation, which considers correlations between all pairs of variables, is given by:

S ≈ S(2) = ΣSi - ΣIij

where Si is the entropy of individual degrees of freedom (e.g., torsion angles), and Iij is the mutual information between variables i and j [3]. The mutual information term Iij = Si + Sj - Sij accounts for both linear and nonlinear correlations [3]. This method has been successfully applied to protein-peptide binding, revealing significant contributions from correlated motions to the overall entropy change [3].

k-th Nearest Neighbor Algorithm

Recent advances in entropy estimation from MD simulations include the k-th nearest neighbor algorithm, which efficiently calculates entropy in high-dimensional spaces by quantifying distances between data points in the conformational space [10]. This method is particularly valuable for capturing complex, multimodal probability distributions that challenge simpler approaches like the quasiharmonic approximation [3] [10].

Diagram 1: Mutual Information Expansion (MIE) workflow for configurational entropy calculation from MD simulations.

Experimental Evidence and Protocols

Isothermal Titration Calorimetry (ITC)

ITC is the primary experimental technique for directly measuring the enthalpy change (ΔH) of binding interactions. By titrating one binding partner into another and measuring the heat released or absorbed, ITC provides complete thermodynamic profiles, including ΔG, ΔH, and TΔS (derived from ΔG = ΔH - TΔS) [3]. Modern automated ITC instruments can measure binding enthalpies with precision sufficient to detect EEC across a series of related compounds.

Protocol for ITC Experiments:

• Precisely dialyze both binding partners into identical buffer solutions to avoid heats of dilution from buffer mismatches
• Degas all solutions to prevent bubble formation in the instrument cell
• Load the cell with the macromolecule (typically 10-100 μM) and the syringe with the ligand (typically 10-20 times higher concentration)
• Set appropriate experimental parameters: temperature, reference power, stirring speed, injection number, volume, and spacing
• Perform control experiments by injecting ligand into buffer and subtract these background heats from the binding data
• Fit the integrated heat data to an appropriate binding model to obtain ΔH, binding constant (Ka), and stoichiometry (n)
• Calculate ΔG = -RTlnKa and TΔS = ΔH - ΔG

NMR Spectroscopy

Nuclear magnetic resonance (NMR) spectroscopy provides site-specific information about molecular motions through generalized order parameters (S²) [3]. These parameters, which range from 0 (completely disordered) to 1 (completely ordered), can be used to estimate changes in configurational entropy upon binding [3].

Protocol for NMR Order Parameter Analysis:

• Collect ¹⁵N relaxation data (T₁, Tâ‚‚, and NOE) for free and bound states of the protein
• Calculate order parameters S² for each residue using model-free analysis or reduced spectral density mapping
• Estimate entropy changes using relationships such as: ΔS = -kBΣ[(3/2)(1-S²) - (1/2)ln(3S²/2)] where the summation is over all bond vectors studied [3]
• Account for limitations including incomplete sampling of all bond vectors and assumptions about probability distributions [3]

Table 2: Quantitative Entropy Changes in Protein-Peptide Binding

System	Total ΔS (kcal mol⁻¹)	Tsg101 ΔS (kcal mol⁻¹)	Ligand ΔS (kcal mol⁻¹)	Method	Reference
Tsg101 UEV/PTAP peptide	-14.0	-12.0	-2.0	MIE/MD	[3]
Tsg101 (torsions only)	-12.0	-10.3	-1.7	MIE/MD	[3]
Tsg101 (angles only)	-1.5	-1.3	-0.2	MIE/MD	[3]
Tsg101 (bonds only)	-0.5	-0.4	-0.1	MIE/MD	[3]

Case Study: Tsg101 UEV Domain-PTAP Peptide Binding

Biological Significance

The UEV domain of the Tsg101 protein binds to the HIV-derived PTAP peptide, playing a crucial role in viral budding [3]. This interaction has been identified as a potential therapeutic target for HIV, making its thermodynamic characterization particularly relevant to drug discovery [3].

Configurational Entropy Analysis

A comprehensive MIE analysis of this system revealed a substantial configurational entropy penalty of -14 kcal mol⁻¹ upon binding [3]. This entropy loss was dominated by torsional degrees of freedom (-12 kcal mol⁻¹), with smaller contributions from angles (-1.5 kcal mol⁻¹) and bonds (-0.5 kcal mol⁻¹) [3]. Notably, the protein (Tsg101) contributed most significantly to the entropy loss (-12 kcal mol⁻¹), while the peptide contributed less (-2 kcal mol⁻¹) [3].

Role of Correlated Motions

The second-order MIE approximation demonstrated that changes in pairwise correlations—captured by the mutual information terms—made major contributions to the overall entropy change [3]. This highlights the importance of accounting for correlated motions in accurate entropy calculations and suggests that binding-induced changes in correlation patterns represent a fundamental aspect of EEC in biomolecular interactions.

Diagram 2: Enthalpy-entropy compensation in protein-ligand binding.

Critical Analysis and Artifact Identification

Statistical Artifacts in EEC

The compelling linearity of ΔH versus ΔS plots does not necessarily indicate genuine compensatory behavior. Several statistical artifacts can produce spurious EEC:

• Error Correlation: Since ΔS is calculated from ΔG and ΔH (ΔS = (ΔH - ΔG)/T), experimental errors in ΔH are directly propagated to ΔS [43]. When |ΔG| < |ΔH|, this error correlation almost guarantees a positive ΔH-ΔS relationship [43].

• Constrained ΔG Range: In biological systems, evolutionary pressures often confine ΔG values to a narrow functional window [43]. For example, protein-ligand binding affinities are typically limited to a biologically useful range, forcing ΔH and ΔS to compensate artificially [43].

Validation Tests

Krug et al. proposed a statistical test to distinguish genuine EEC from artifacts [43]. For a ΔH-ΔS correlation to be significant, the experimental temperature T should fall outside the 95% confidence interval of the compensation temperature Tc:

|T - Tc| > 1.96σ

where σ is the standard error of Tc from linear regression [43]. Application of this test to published protein data sets revealed that many purported examples of EEC could be explained by statistical artifacts rather than genuine compensatory behavior [43].

Evolutionary and Practical Implications

Evolutionary Adaptation

Recent research indicates that EEC plays a crucial role in protein evolution. Ancestral sequence reconstruction studies suggest that ancient proteins likely exhibited entropically favored, flexible binding modes, while modern proteins have evolved toward enthalpically driven specificity [44] [45]. This thermodynamic trade-off enables proteins to maintain optimal binding affinity despite environmental fluctuations, including temperature variations [44].

Drug Discovery Applications

In pharmaceutical research, understanding EEC is essential for rational drug design. The characteristic "flat" structure-activity relationships observed in many medicinal chemistry campaigns—where significant structural modifications produce minimal changes in binding affinity—often reflect EEC [43] [44]. By deliberately manipulating the enthalpy-entropy balance, researchers can optimize not only binding affinity but also drug properties such as specificity, solubility, and resistance profiles [44].

Table 3: Research Reagent Solutions for Thermodynamic Studies

Reagent/Resource	Function	Application Example
Isothermal Titration Calorimeter	Directly measures binding enthalpy	Determining ΔH for protein-ligand interactions [3]
High-Field NMR Spectrometer	Measures molecular motions via relaxation	Determining order parameters for entropy calculation [3]
Molecular Dynamics Software	Simulates molecular motions	Generating trajectories for entropy analysis [3] [10]
Stable Isotope-Labeled Proteins	Enables NMR studies of large proteins	Producing ¹⁵N, ¹³C-labeled proteins for dynamics studies [3]
Mutual Information Expansion Code	Computes entropy from correlations	Implementing MIE analysis on MD trajectories [3] [10]

Enthalpy-entropy compensation represents a fundamental trade-off in molecular interactions with far-reaching implications for understanding and manipulating biological processes. While statistical artifacts can produce spurious compensation patterns, genuine EEC provides insights into the intimate connection between energy and disorder in molecular systems. The integration of advanced computational methods like mutual information expansion with experimental techniques such as ITC and NMR has significantly enhanced our ability to quantify configurational entropy changes and unravel the thermodynamic drivers of biomolecular recognition.

For drug development professionals, a sophisticated understanding of EEC enables more rational optimization strategies that move beyond simple affinity measurements to consider the precise thermodynamic signatures of molecular interactions. As research in this field advances, the continuing integration of thermodynamic principles with structural and evolutionary biology promises to yield novel approaches for addressing challenging therapeutic targets.

The desolvation problem represents a fundamental challenge in molecular recognition, particularly in structure-based drug design. Binding affinity is determined by the delicate balance between the energetic gains from forming new intermolecular interactions and the penalties associated with stripping solvating water molecules from binding interfaces. This whitepaper examines how configurational entropy and solvation thermodynamics govern molecular interactions, drawing upon recent advances in computational and experimental biophysics. We provide a quantitative framework for understanding how hydrophobic desolvation, frustration of hydration, and conformational changes collectively influence binding equilibria, with direct implications for rational drug design and protein engineering.

Molecular binding in aqueous solution is most accurately conceptualized not as a simple association reaction, but as an exchange reaction in which some receptor-solvent and ligand-solvent interactions are lost to accommodate the gain of receptor-ligand interactions in the bound complex [46]. The binding free energy (ΔG) that determines the stability of the resulting complex is governed by the classic thermodynamic relationship: ΔG = ΔH - TΔS, where ΔH represents the enthalpy change and ΔS the entropy change associated with binding [47].

The desolvation problem arises because this free energy balance must account for the significant energetic costs of dehydrating binding surfaces. When two molecules form a complex, they must first strip away the hydrating water molecules to make direct contact. This process is energetically unfavorable if the lost water-solute interactions are stronger than the water-water interactions in bulk solution. Understanding this balance is crucial for predicting and optimizing molecular interactions in research applications ranging from drug discovery to protein engineering.

Theoretical Framework: Solvation, Entropy, and Binding

The Nature of the Desolvation Penalty

Desolvation penalties are particularly significant for polar atoms that form strong, directional interactions with water molecules. The transfer of such atoms from an aqueous environment to a protein binding pocket incurs a substantial free energy cost if the new interactions with the protein do not fully compensate for the lost water interactions [46]. This explains why adding polar groups to ligands does not always improve binding affinity, despite the potential for forming additional hydrogen bonds with the target protein [47].

The hydrophobic effect, which drives the association of nonpolar surfaces, is largely attributed to entropic gains when ordered water molecules are released from hydrophobic surfaces into the bulk solvent [48] [47]. However, experimental studies using isothermal titration calorimetry (ITC) have revealed that the hydrophobic effect can also have a significant enthalpic component [47], highlighting the complexity of solvation thermodynamics.

Configurational Entropy in Molecular Recognition

Configurational entropy quantifies the number of accessible molecular arrangements within a system and is a critical parameter in understanding thermodynamic properties, binding affinities, and structural dynamics [10]. Upon binding, both the protein and ligand typically experience a reduction in conformational flexibility, which represents an unfavorable entropic penalty that opposes binding.

However, this penalty can be mitigated through several mechanisms:

• Pre-organization: If the ligand is already somewhat pre-organized or rigid in its unbound state, the conformational change upon binding is smaller, resulting in a less significant entropy loss [47].
• Solvent entropy gain: The release of ordered water molecules from binding sites into bulk solvent can provide a compensating entropic gain that drives binding [47].
• Entropy redistribution: Proteins sometimes counterbalance unfavorable entropy decreases within binding pockets by redistributing dynamics to other regions of the protein structure [47].

Table 1: Thermodynamic Components of Molecular Recognition

Component	Typical Effect on Binding	Structural Origin
Enthalpy (ΔH)	Favorable (negative) when strong interactions form	Hydrogen bonds, van der Waals contacts, electrostatic interactions
Configurational Entropy (-TΔS)	Unfavorable (positive) due to restricted mobility	Loss of rotational, translational, and conformational freedom
Solvation Entropy	Can be favorable when ordered waters are released	Hydrophobic effect, displacement of tightly-bound waters
Desolvation Penalty	Unfavorable (positive) for polar groups	Energetic cost of dehydrating polar atoms before binding

Quantitative Studies and Experimental Evidence

Dissecting Cooperativity in Protein Folding

Studies on consensus ankyrin repeat proteins (CARPs) with nearly identical repeat sequences have enabled precise quantification of cooperativity by resolving stability into intrinsic and interfacial components [48]. Applying a one-dimensional Ising model to a series of constructs revealed that:

• Intrinsic folding is entropically disfavored, involving chain entropy decrease and backbone ordering
• Interfacial interaction is entropically favored and attends a decrease in heat capacity
• Hydrophobic desolvation occurs upon interfacial interaction, contributing significantly to cooperativity [48]

These findings suggest that helix formation and backbone ordering occurs upon intrinsic folding, whereas hydrophobic desolvation occurs during interfacial interaction, highlighting the distinct thermodynamic contributions to cooperative folding.

Configurational Entropy in HDAC2-Inhibitor Binding

Research on histone deacetylase 2 (HDAC2) inhibitors has demonstrated the significant role of configurational entropy in molecular recognition. Molecular dynamics simulations and entropy calculations for five HDAC2-inhibitor complexes revealed:

• Configurational entropic contributions ranged widely from 2.75 to 16.38 kcal/mol for the five inhibitors examined [49]
• For structurally similar carbamide ligands, the levels of entropic contribution were comparable
• For structurally unrelated ligands, entropic contributions differed significantly [49]

These findings exemplify the importance of assessing molecular dynamics and estimating entropic contributions when evaluating ligand binding mechanisms, as entropy can have different levels of impact on molecular recognition depending on the specific system.

Table 2: Experimental Measurements of Desolvation and Entropic Effects

System Studied	Experimental Method	Key Findings	Reference
Consensus ankyrin repeat proteins	Thermal & chemical denaturation with Ising model analysis	Interfacial interaction entropically favored with heat capacity decrease suggesting hydrophobic desolvation	[48]
HDAC2-inhibitor complexes	MD simulations with configurational entropy estimation	Entropic contributions range from 2.75-16.38 kcal/mol depending on ligand structure	[49]
Heteroaromatic stacking interactions	Grid Inhomogeneous Solvation Theory (GIST)	Good correlation between estimated desolvation penalty and experimental binding free energy	[50]
Hydration frustration	Alkane/water partition coefficients	Proximal polar atoms in binding sites can have frustrated hydration, affecting binding affinity	[46]

Methodologies for Quantifying Desolvation and Entropy

Computational Approaches

Grid Inhomogeneous Solvation Theory (GIST)

GIST enables a thermodynamic analysis of water molecules based on molecular dynamics trajectories using a grid-based approach [50]. This method calculates the solvation free energies of molecular fragments and complexes to estimate the desolvation penalty upon binding. In studies of heteroaromatics in complex with truncated amino acid side chains, GIST calculations have shown good correlation between the estimated desolvation penalty and experimental binding free energy [50].

The GIST methodology involves:

• Performing MD simulations of the solute in explicit solvent
• Discretizing the simulation space into a grid of voxels
• Calculating thermodynamic quantities for water molecules in each voxel
• Integrating these quantities to obtain total solvation free energies

Configurational Entropy Estimation

Several computational methods have been developed to estimate configurational entropy from molecular dynamics simulations:

• Quasi-harmonic approximation (QH): Estimates configurational entropy by building a Gaussian distribution of protein conformations [49]
• kth nearest neighbor method: A statistical approach for estimating entropy by quantifying distances between data points in high-dimensional spaces [10]
• Mutual information expansion (MIE): Accounts for correlations between different degrees of freedom when calculating configurational entropy [10]
• Multiscale cell correlation method: Decomposes total entropy into translational, rotational, and topographical components [10]

Diagram 1: Configurational Entropy Calculation Workflow. This diagram illustrates the computational workflow for estimating configurational entropy from molecular dynamics simulations using various methodological approaches.

Experimental Approaches

Partition Coefficient Measurements

Partition coefficients between water and nonpolar solvents provide experimental insights into solvation thermodynamics. While octanol/water partition coefficients (logP) are commonly used in drug discovery, they are less ideal for studying fundamental solvation properties because octanol can form hydrogen bonds with solutes [46].

Alkane/water partition coefficients (e.g., cyclohexane/water or hexadecane/water) provide better models for assessing hydrophobic effects and desolvation penalties because the saturated hydrocarbon lacks hydrogen bonding capability [46]. The difference between octanol/water and alkane/water partition coefficients (ΔlogP) quantifies a solute's capacity for hydrogen bonding [46].

Isothermal Titration Calorimetry (ITC)

ITC directly measures the enthalpy change (ΔH) upon binding and allows calculation of the entropic contribution (-TΔS) through the relationship -TΔS = ΔG - ΔH. ITC studies have revealed that the hydrophobic effect can have significant enthalpic components, challenging the traditional view that it is primarily entropy-driven [47].

The Scientist's Toolkit: Essential Research Reagents and Methods

Table 3: Research Reagent Solutions for Studying Desolvation and Entropy

Tool/Reagent	Function	Application Context
Consensus ankyrin repeat proteins (CARPs)	Minimalist protein system with nearly identical repeats	Quantifying cooperativity and resolving intrinsic vs. interfacial folding components [48]
Grid Inhomogeneous Solvation Theory (GIST)	Computational method for solvation thermodynamics	Estimating desolvation penalties for molecular complexes [50]
Alkane/water partition coefficients	Experimental measurement of solvation energy	Assessing hydrophobic effect and hydrogen bonding capacity [46]
Isothermal Titration Calorimetry (ITC)	Direct measurement of binding thermodynamics	Determining enthalpic and entropic contributions to binding [47]
Molecular Dynamics (MD) Simulations	Atomic-level sampling of molecular motions	Calculating configurational entropy and desolvation dynamics [49] [10]
Quasi-harmonic Approximation	Computational entropy estimation	Calculating configurational entropy from MD trajectories [49]
OB-1-d3	OB-1-d3, MF:C21H17N3O6, MW:410.4 g/mol	Chemical Reagent
ST-1006	ST-1006, MF:C16H20Cl2N6, MW:367.3 g/mol	Chemical Reagent

Practical Applications in Drug Design

Leveraging Hydration Frustration

Frustrated hydration occurs when two or more polar atoms in a binding site are positioned such that water molecules cannot simultaneously form ideal interactions with all of them due to unfavorable water-water interactions [46]. This phenomenon can be exploited in drug design by creating ligands with complementary polar groups that can simultaneously engage the frustrated polar atoms, as the energetic penalty for desolvation has already been paid by the binding site [46].

Managing the Desolvation Penalty

Strategic approaches to managing desolvation penalties in drug design include:

• Avoiding excessive polarity: Adding polar groups to surface-exposed regions of ligands may not improve binding due to high desolvation costs [47]
• Targeting frustrated hydration sites: These sites offer opportunities for forming multiple polar interactions with reduced desolvation penalty [46]
• Pre-organizing ligand conformation: Reducing the entropic penalty upon binding by designing ligands that already resemble the bound conformation [47]

Diagram 2: Desolvation-Aware Ligand Design Strategy. This diagram outlines a strategic approach to ligand design that accounts for the hydration state of binding sites to minimize desolvation penalties.

The desolvation problem represents a central challenge in molecular recognition that requires careful consideration of both interaction gains and solvation losses. Configurational entropy plays a crucial role in this balance, influencing binding affinity through its effects on molecular flexibility and solvent reorganization. Successful molecular design strategies must account for the complex interplay between enthalpic interactions, configurational entropy, and solvation thermodynamics.

Advances in computational methods, particularly molecular dynamics simulations with improved entropy estimation algorithms, coupled with experimental approaches using model systems and precise thermodynamic measurements, are providing increasingly sophisticated tools to quantify and manage the desolvation problem. By integrating these approaches, researchers can develop more effective strategies for optimizing molecular interactions in drug design, protein engineering, and molecular recognition research.

Configurational entropy represents a fundamental component of the free energy landscape governing intermolecular interactions, particularly in drug discovery. When a ligand binds to its biological target, it typically loses a significant degree of conformational, rotational, and translational freedom, resulting in an entropic penalty that opposes binding. Within the broader context of intermolecular interactions research, understanding and managing this entropic cost is paramount for designing high-affinity therapeutic compounds. Strategies aimed at pre-organizing ligands in their bio-active conformation and reducing rotational freedom directly address this challenge by minimizing the entropic penalty paid upon binding. This whitepaper examines advanced experimental and computational strategies for entropic optimization, providing researchers with methodologies to enhance binding affinity through rational manipulation of thermodynamic parameters.

Theoretical Foundation: Entropic Contributions to Binding Free Energy

The binding free energy (ΔG) is governed by the classical thermodynamic relationship ΔG = ΔH - TΔS, where ΔH represents the enthalpy change, T is the temperature, and ΔS represents the entropy change. The overall binding entropy change (ΔS_bind) comprises multiple components [51]:

• Configurational Entropy (ΔS_conf): The loss of conformational degrees of freedom for both ligand and protein upon binding.
• Solvation Entropy (ΔS_solv): Changes in solvent organization, including hydrophobic and polarization effects.
• Rotational/Translational Entropy (ΔS_rt): The loss of overall rotational and translational freedom.

The conformational entropy change is typically unfavorable (ΔSconf < 0), as the process of binding restricts molecular motion, while solvation entropy is usually favorable (ΔSsolv > 0) due to desolvation effects [51]. The art of entropic optimization lies in minimizing the unfavorable components while maximizing the favorable ones.

Table 1: Thermodynamic Components of Ligand Binding

Component	Typical Effect on Binding	Molecular Origin	Optimization Strategy
Configurational Entropy (ΔS_conf)	Unfavorable	Loss of ligand and protein flexibility	Ligand pre-organization; rigid scaffold design
Hydrophobic Entropy (ΔS_hphob)	Favorable	Release of ordered water molecules from hydrophobic surfaces	Maximizing non-polar surface area burial
Polarization Entropy (ΔS_pol)	Variable	Reorganization of polar groups and electrostatic interactions	Optimizing electrostatic complementarity
Rotational/Translational Entropy (ΔS_rt)	Unfavorable	Restriction of whole-body motions	Increasing effective molecular weight upon binding

Strategic Approach I: Ligand Pre-organization

Fundamental Principles and Design Considerations

Ligand pre-organization involves designing molecules that already exist predominantly in their receptor-bound conformation before binding occurs, thereby minimizing the entropic cost associated with restricting flexible degrees of freedom. This strategy effectively transfers the entropic penalty from the binding event to the synthetic design phase, resulting in enhanced binding affinity.

A compelling example comes from recent research on cucurbit[7]uril (CB[7]) complexes, where halogenated N-phenylpiperazine derivatives demonstrated how strategic fluorination can enforce pre-organization. The introduction of ortho-fluorine atoms promoted intramolecular C–H⋯F interactions that locked the ligand into a binding-competent conformation, significantly reducing the entropic penalty upon complexation [52]. This pre-organization effect was determined to be a major factor in the enhanced binding affinity observed for ortho-fluorinated compounds compared to their non-halogenated or para-substituted analogues.

Quantitative Analysis of Pre-organization Effects

Table 2: Thermodynamic Parameters for Halogenated N-phenylpiperazine Derivatives Binding to CB[7] [52]

Ligand Substituent	Position	ΔG (kcal/mol)	ΔH (kcal/mol)	-TΔS (kcal/mol)	Key Observation
F	ortho	-6.2	-4.8	-1.4	Optimal pre-organization via C–H⋯F
Cl	ortho	-5.9	-5.1	-0.8	Enhanced dispersion, moderate pre-organization
F	para	-5.5	-5.0	-0.5	Minimal pre-organization effect
Br	para	-5.8	-5.5	-0.3	Portal interaction, enthalpic driven
None	-	-5.2	-4.7	-0.5	Baseline flexibility

The data reveals that ortho-fluorination provides the most favorable binding free energy, primarily through a reduction in the entropic penalty (-TΔS term), consistent with the pre-organization hypothesis. In contrast, larger halogens at the para position enhance binding predominantly through enthalpic contributions, likely through interactions with the CB[7] portal.

Strategic Approach II: Reducing Rotational Freedom

Conformational Restriction Techniques

Reducing rotational freedom involves the introduction of structural constraints that limit the number of accessible low-energy conformations. Common approaches include:

• Macrocyclization: Creating cyclic structures that lock rotational bonds
• Steric Hindrance: Introducing bulky substituents that physically impede rotation
• Intramolecular Bridging: Adding covalent links between previously rotatable segments
• Ring Fusion: Incorporating rigid polycyclic systems

The thermodynamic benefit of these strategies was quantified in a study of 233 protein-ligand complexes, which revealed that "the ligand conformation in the bound state was significantly different from the most favorable conformation in solution" in most cases, and that "both entropic and enthalpic contributions to this free energy change are significant" [53]. This underscores the importance of properly evaluating the free energy consequences of conformational restriction.

Global Dynamic Effects on Protein Entropy

An often-overlooked aspect of entropy optimization involves effects on protein dynamics. Research on the arabinose-binding protein (ABP) demonstrated that ligand binding can cause "a global increase in the extent of protein dynamics on the pico- to nanosecond timescale" throughout the protein, with exception of binding site residues which showed restricted dynamics [54]. This global dynamic change constitutes a substantial favorable entropic contribution to binding, suggesting that some protein structures may be evolutionarily adapted to exploit dynamic changes to reduce the net entropic cost of binding.

Diagram 1: Conformational Entropy Penalty in Ligand Binding

Experimental Methodologies for Quantifying Entropic Contributions

Isothermal Titration Calorimetry (ITC) Protocol

ITC represents the gold standard for experimentally determining thermodynamic parameters of binding interactions, providing direct measurements of ΔG, ΔH, and TΔS.

Detailed Experimental Protocol [52]:

• Instrument Calibration: Perform electrical calibration and verification tests according to manufacturer specifications
• Sample Preparation:
  • Dissolve CB[7] in acetic acid-sodium acetate buffer (20 mM, pH 4.0) at concentrations of 0.25-4.0 mM
  • Prepare ligand solutions in identical buffer at concentrations of 1.25-30.0 mM
  • Degas all solutions for 10 minutes to eliminate air bubbles
• Titration Parameters:
  • Cell temperature: 25°C
  • Reference power: 5-10 μcal/sec
  • Stirring speed: 750 rpm
  • Injection sequence: 20 injections of 2 μL each with 120-second intervals
• Control Experiments: Perform blank titrations of ligand into buffer to quantify dilution heats
• Data Analysis: Fit raw data using appropriate binding models (e.g., one-site binding) in MicroCal PEAQ-ITC Analysis Software v1.41

Restraint Release (RR) Computational Approach

The RR approach provides a microscopic method for evaluating configurational entropy contributions by calculating the free energy associated with releasing harmonic restraints applied to the ligand.

Computational Protocol [51]:

• System Setup:
  • Obtain protein-ligand coordinates from Protein Data Bank
  • Add hydrogen atoms and water molecules using molecular modeling software (e.g., MOLARIS)
  • Determine ionization states of protein residues at physiological pH
• Equilibration:
  • Perform 2ps molecular dynamics at 300K with 0.5fs timesteps
  • Apply weak harmonic constraints (0.01 kcal mol⁻¹Å⁻²) to protein atoms beyond 18Ã… sphere
• Restraint Application:
  • Apply strong Cartesian restraints to ligand atoms in both bound and unbound states
  • Systematically vary restraint coordinates to identify minimization set
• Free Energy Calculation:
  • Use Free Energy Perturbation (FEP) to compute restraint release free energies
  • Calculate entropy differences between restrained and unrestrained states

Diagram 2: Restraint Release Method Thermodynamic Cycle

Crystallography and Structure Analysis

X-ray crystallography provides structural insights into pre-organization phenomena and binding modes.

Crystallization Protocol [52]:

• Complex Preparation: Dissolve CB[7] and ligand in appropriate buffer at elevated temperature
• Crystal Growth: Slowly cool solutions and allow slow evaporation over days to weeks
• Data Collection: Collect X-ray diffraction data at 100K using CuKα radiation (λ = 1.54 Ã…)
• Structure Solution: Solve structures using SHELXT and refine with SHELXL

Table 3: Key Research Reagents and Computational Tools for Entropic Studies

Item	Function/Application	Example Sources/Platforms
Cucurbit[7]uril (CB[7])	Model host system for studying supramolecular recognition	BLD Pharm [52]
Halogenated N-phenylpiperazine Derivatives	Guest molecules for investigating halogen effects on binding	Merck/Sigma Aldrich [52]
MicroCal PEAQ-ITC	Instrument for direct thermodynamic measurements	Malvern Panalytical [52]
MOLARIS/ENZYMIX	Software for molecular simulations and entropy calculations	University of Southern California [51]
Symmetry-Adapted Perturbation Theory (SAPT)	Computational method for energy decomposition	Various quantum chemistry packages [52]
Attach-Pull-Release (APR)	Free energy calculation method	University of Utah [52]

The strategic optimization of entropic contributions through ligand pre-organization and reduction of rotational freedom represents a powerful approach in rational drug design. The integration of experimental methodologies like ITC and XRD with advanced computational approaches such as the Restraint Release method and SAPT analysis provides researchers with a comprehensive toolkit for quantifying and manipulating these crucial thermodynamic parameters. As structural biology and computational methods continue to advance, the ability to precisely engineer entropic contributions will undoubtedly play an increasingly important role in the development of high-affinity therapeutic compounds, catalyst design, and molecular recognition systems. Future research directions will likely focus on more sophisticated dynamic pre-organization strategies that exploit global protein dynamics to further optimize the entropic costs of binding.

Water displacement and the hydrophobic effect represent fundamental drivers of molecular recognition and association in aqueous biological systems. The expulsion of solvent water from binding interfaces and nonpolar surfaces is a critical process governed by complex thermodynamic changes, particularly in configurational entropy. This technical review examines the intricate balance of enthalpic and entropic contributions to the free energy of binding, with emphasis on quantitative frameworks for predicting affinity and designing targeted interactions. Through integrated computational, spectroscopic, and thermodynamic approaches, researchers are unraveling how water molecules mediate biomolecular interactions—from protein-ligand binding to DNA-drug recognition—enabling more sophisticated manipulation of these forces in pharmaceutical development and materials science.

Biological processes occur in aqueous environments where water molecules function not merely as passive spectators but as active determinants of structure, affinity, and specificity. The hydrophobic effect—the tendency of nonpolar surfaces to associate in water—has long been recognized as a major driving force in biology, stabilizing structures ranging from protein cores to cellular membranes [55]. Traditional views emphasized the entropy gain resulting from water reorganization, but recent research reveals a more nuanced picture where both enthalpic and entropic contributions vary significantly with system characteristics and conditions.

The displacement of water molecules from binding sites during molecular recognition events represents a critical thermodynamic process with profound implications for configurational entropy. When a ligand binds to a protein or when two hydrophobic surfaces associate, high-energy water molecules are released from constrained positions into the bulk solvent, resulting in entropy gain that frequently drives the interaction free energy [56] [57]. Understanding the precise thermodynamics of these water networks has become a central focus in structural biology and drug design, enabling researchers to exploit water displacement for enhancing binding affinity and specificity.

Theoretical Framework: Thermodynamics of Water Displacement

The Hydrophobic Effect at Molecular Scales

The hydrophobic effect operates differently at molecular scales compared to macroscopic phase separation. For molecular binding, the free energy penalty of hydrating nonpolar surfaces drives association, with the magnitude of this penalty proportional to the buried surface area. Seminal molecular dynamics simulations quantified this relationship, demonstrating that the free energy of hydrophobic cluster formation is proportional to the loss in exposed molecular surface area with a constant of proportionality of 45 ± 6 cal/mol·Å² (or 24 cal/mol·Å² when converted to solvent-accessible surface area) [55]. This quantitative relationship provides a fundamental basis for predicting binding affinities in drug design.

The thermodynamic signature of the hydrophobic effect varies significantly with temperature and system characteristics. While classical descriptions emphasized entropy dominance at room temperature, contemporary research reveals more complex behavior:

• Cavity water encapsulated in hydrophobic binding sites can exist in thermodynamically unfavorable states, with free energy costs of displacement ranging from 0 to +37 kcal mol⁻¹ in model systems [56]
• Enthalpy-entropy compensation frequently occurs, where favorable entropy gains are partially offset by enthalpy costs, complicating simple predictions of binding favorability
• Non-classical hydrophobic effects with enthalpy-driven binding can emerge in confined spaces with specific hydration properties [56]

Configurational Entropy and Water Networks

Configurational entropy changes arising from water reorganization represent a crucial component of the binding free energy. When water molecules transition from constrained positions in binding sites to the bulk solvent, they gain rotational, translational, and vibrational freedom, resulting in entropy increases that drive spontaneous association. Recent studies quantify how hydrogen-bond network restructuring influences this entropy gain, with demonstrated free energy barrier reductions of 1-2 kcal·mol⁻¹ corresponding to order-of-magnitude enhancements in reaction rates [58].

The local hydrogen-bond architecture dramatically influences water reactivity and thermodynamics. Research comparing slab versus nanodroplet interfaces reveals that microscopic inhomogeneity in nanodroplets traps water in donor-acceptor dimer configurations, while more homogeneous H-bond networks at slab interfaces create distinct entropy profiles [58]. This quantified difference in solvation configurational entropy directly translates to measurable variations in chemical reactivity and binding affinity.

Table 1: Quantitative Measures of Hydrophobic Interactions and Water Displacement

Parameter	Value	System	Significance
Hydrophobic interaction energy	24 cal/mol·Å²	Methane clusters in water	Quantifies driving force for nonpolar surface burial [55]
Water displacement free energy cost	0 to +37 kcal mol⁻¹	Cucurbit[8]uril host-guest systems	Range of thermodynamic penalties for cavity water [56]
Entropy-driven barrier reduction	1-2 kcal·mol⁻¹	Slab vs. nanodroplet interfaces	Free energy change from H-bond network restructuring [58]
H-bonded vs. free O-H bond energy difference	0.74 kcal/mol	Air-water interface	Single-point energy difference at CCSD(T)/aug-cc-pV5Z level [58]

Experimental Evidence and Methodologies

Computational Approaches: Molecular Dynamics Simulations

Molecular dynamics (MD) simulations provide atomic-level insights into water behavior during binding events. The following protocol exemplifies approaches for quantifying hydrophobic interactions:

Protocol: Molecular Dynamics Analysis of Hydrophobic Cluster Formation [55]

• System Preparation: Create simulation boxes with 1-112 solute molecules (methane, butane, isobutylene, or benzene) in water-filled boxes of varying sizes (6,500 to 52,000 ų containing 204-1,726 water molecules)
• Simulation Parameters:
  • Ensemble: NVE (constant number of molecules, volume, and energy)
  • Duration: 1 ns at 298 K
  • Time step: 2 fs
  • Solvent model: Fully flexible three-centered water
  • Solute representation: All-atom with periodic boundary conditions
• Cluster Analysis:
  • Use Voronoi polyhedron method to determine atomic contacts and molecular surface areas
  • Calculate solvent-exposed and buried surface areas for clusters at each time step
  • Determine equilibrium constants for sequential solute addition to clusters
• Free Energy Calculation: Compute directly from distribution of cluster sizes observed in trajectories using the relationship ΔG = -RTlnK

This methodology enables direct quantification of the hydrophobic interaction from simulation data, revealing how intermittent cluster formation gives free energy proportional to buried molecular surface area.

Advanced Spectroscopic Techniques: Chiral Vibrational Sum Frequency Generation

Chiral vibrational sum frequency generation (chiral SFG) spectroscopy enables in situ probing of hydration structure changes during binding events. Recent applications to DNA-drug interactions demonstrate precise detection of water displacement from specific sites:

Protocol: Chiral SFG Analysis of DNA Hydration Changes [59]

• Sample Preparation: Drop-cast (dA)₁₂·(dT)₁₂ dsDNA on quartz surface with varying molar ratios of netropsin to DNA (0:1, 1:1, 1.5:1, 2:1)
• Spectral Acquisition:
  • Beam configuration: s-polarized visible beam and p-polarized infrared beam
  • Detection: p-polarized SFG signals
  • Phase-resolved internal heterodyne detection for enhanced sensitivity
  • Spectral range: Covering OH stretches (3000-3600 cm⁻¹)
• Spectral Analysis:
  • Global fitting with multiple peaks (∼3209 cm⁻¹, ∼3347 cm⁻¹, ∼3400 cm⁻¹)
  • Assignment to specific vibrational modes (NH stretches, strongly H-bonded water, weakly H-bonded water)
  • Correlation with molecular dynamics simulations
• MD Integration:
  • Build hydrated molecular models of DNA with 0, 1, and 2 netropsin molecules
  • Run 100 ns MD simulations with DNA helical axis aligned with simulation cell z-axis
  • Simulate chiral SFG response using water OH electrostatic map
  • Analyze first hydration shell waters in minor groove, major groove, and backbone

This combined experimental-computational approach demonstrated that netropsin binding preferentially displaces strongly hydrogen-bonded water molecules from the DNA minor groove, with signal reductions proportional to drug occupancy [59].

Thermodynamic Profiling of Binding Sites

Computational tools like ColdBrew leverage water network analysis to predict favorable binding sites and optimize ligand interactions. This algorithm addresses artifacts from cryogenic structural techniques by predicting water molecule positions at physiological temperatures:

Protocol: ColdBrew Implementation for Drug Binding Site Analysis [60]

• Data Collection: Access precalculated ColdBrew datasets spanning >100,000 predictions covering 46 million water molecules from the Protein Data Bank
• Water Likelihood Assessment: For each water molecule in experimental protein structures, compute probability of presence at higher temperatures
• Binding Site Prioritization: Identify sites where water displacement would yield maximal entropy gain, focusing on locations with tightly-bound, high-energy waters
• Ligand Design Optimization: Incorporate water displacement energetics into ligand modification strategies, targeting sites with thermodynamically unfavorable waters

This approach has revealed that experienced drug designers intuitively avoid tightly-bound waters, suggesting that explicit consideration of water displacement thermodynamics could systematize and accelerate this process [60].

Table 2: Experimental Methods for Studying Water Displacement and Entropy Gain

Method	Key Measurements	Applications	Technical Requirements
Molecular Dynamics Simulations	Potential of mean force, radial distribution functions, H-bond lifetimes	Host-guest systems, protein-ligand binding, hydrophobic aggregation [56] [55]	High-performance computing, explicit solvent models
Chiral SFG Spectroscopy	OH stretch intensities, frequency shifts, phase resolution	DNA hydration changes, protein hydration dynamics, chiral supramolecular structures [59]	Laser systems, surface preparation, phase-sensitive detection
ColdBrew Computational Tool	Water presence probability, hydration site energetics	Drug binding site prediction, ligand design optimization [60]	Protein Data Bank structures, computational resources
Thermodynamic Analysis	Binding free energy, enthalpy, entropy, heat capacity	Structure-activity relationships, drug affinity optimization [57] [61]	Calorimetry, temperature-dependent studies

Table 3: Research Reagent Solutions for Water Displacement Studies

Resource	Function	Application Context
ColdBrew Database	Precalculated water positions and probabilities for protein structures	Predicting water displacement energetics in drug design [60]
Cucurbit[8]uril Host Models	Idealized systems with tunable host-water interactions	Isolating hydration effects in molecular recognition [56]
Chiral SFG Instrumentation	Surface-specific vibrational spectroscopy of hydration layers	Probing water structure changes at biomolecular interfaces [59]
Polarizable Water Models	Accurate representation of water electronic structure	Molecular dynamics simulations of hydrophobic interactions [58]
Hydrophobic Ion Pairing Reagents	Enable co-loading of water-soluble drugs in delivery systems	Formulating hydrophilic pharmaceuticals in polymeric micelles [62]

The displacement of water molecules and the associated entropy gain represent fundamental processes driving molecular associations in biological systems. Quantitative understanding of these phenomena has advanced significantly through integrated computational, spectroscopic, and thermodynamic approaches, revealing both the complexity and predictability of water-mediated interactions.

The emerging paradigm recognizes water not as a passive background solvent but as an active, manipulable component in molecular recognition. Research demonstrates that targeted displacement of high-energy water molecules from binding sites can enhance affinity, while conservation of tightly-bound waters can maintain specificity. These principles are now being systematically applied in pharmaceutical development, with computational tools like ColdBrew enabling prediction of water displacement consequences before synthetic investment [60].

Future research directions will likely focus on extending these principles to dynamic binding processes, multi-component systems, and in vivo environments. As quantification of configurational entropy contributions becomes more precise, researchers will increasingly engineer water-mediated interactions with predictable thermodynamic outcomes, advancing both fundamental understanding and practical applications in drug discovery and materials design.

The evolution of drug candidates from first-in-class to best-in-class status represents a critical pathway in modern therapeutics development. This whitepaper examines the fundamental thermodynamic principles—specifically the interplay between binding enthalpy (ΔH) and entropy (TΔS)—that distinguish pioneering drugs from their optimized successors. Through analysis of documented drug classes, including HIV-1 protease inhibitors and statins, we demonstrate that best-in-class inhibitors consistently achieve superior binding affinity through improved enthalpic contributions, often overcoming the initial entropic dominance of first-in-class compounds. The critical role of configurational entropy in modulating these interactions is explored through advanced computational methodologies, particularly the Mutual Information Expansion (MIE) approach applied to molecular dynamics simulations. Our findings provide researchers with a structured framework for integrating thermodynamic profiling and entropy-aware optimization into rational drug design paradigms, accelerating the development of high-affinity, selective therapeutic agents.

Drug discovery and optimization represent a monumental challenge in biomedical science, where the ultimate goal is to develop therapeutic agents that bind their targets with exceptional affinity and specificity. The binding affinity (Ka) is fundamentally governed by the Gibbs free energy equation (ΔG = ΔH - TΔS), establishing that extreme affinity requires favorable contributions from both enthalpy (ΔH) and entropy (ΔS) [63] [64]. Despite this thermodynamic reality, first-in-class drug candidates frequently emerge as suboptimal from an enthalpic perspective, relying predominantly on entropic driving forces—primarily the hydrophobic effect—for their binding energy [64].

The transition from first-in-class to best-in-class status typically involves a systematic improvement in binding enthalpy, a parameter notoriously difficult to optimize due to the precise geometric constraints of hydrogen bonding and van der Waals interactions, coupled with significant desolvation penalties for polar groups [64]. Meanwhile, configurational entropy—the entropy associated with the loss of conformational degrees of freedom upon binding—represents a substantial unfavorable component that must be overcome. Recent advances in computational biophysics, particularly methods for quantifying configurational entropy changes from molecular dynamics simulations, are providing unprecedented insights into these molecular interactions [3] [10].

This technical review examines the documented thermodynamic trajectories of evolved drug classes, details experimental and computational methodologies for thermodynamic profiling, and establishes a framework for leveraging configurational entropy analysis in targeted drug development.

Thermodynamic Foundations of Molecular Recognition

Fundamental Forces in Binding Interactions

The binding interaction between a drug molecule and its biological target is governed by a complex interplay of opposing forces. The overall binding free energy (ΔG) comprises two primary components:

• Enthalpic Contributions (ΔH): Result from attractive forces including van der Waals interactions and hydrogen bonding between drug and protein, counterbalanced by the unfavorable enthalpy associated with desolvation of polar groups. Hydrogen bonding optimization requires precise distance and angular geometry, as suboptimal bonding can result in net unfavorable enthalpy due to the significant penalty for dehydrating polar groups (approximately 8 kcal/mol at 25°C) [64].

• Entropic Contributions (-TΔS): Arise primarily from two sources: the favorable desolvation entropy from water release as drug and binding cavity undergo desolvation, and the unfavorable conformational entropy loss as both drug and target lose degrees of freedom upon binding [64].

The Challenge of Enthalpic Optimization

Enthalpic optimization presents particular difficulties in rational drug design. While entropy can be readily improved through hydrophobic group incorporation, engineering favorable enthalpy requires precise positioning of hydrogen bond donors and acceptors to form interactions stronger than those they maintain with water molecules in solution. Current structure-based drug design lacks the precision to engineer hydrogen bonds to the tenths of angstroms necessary for net favorable enthalpy, making it a protracted process often requiring iterative structural modifications over many years [64].

Table 1: Thermodynamic Components of Binding Interactions

Component	Molecular Origin	Optimization Challenge
Favorable Enthalpy (ΔH)	Van der Waals contacts, Hydrogen bonds	Requires precise geometric complementarity; must overcome desolvation penalties
Unfavorable Enthalpy	Desolvation of polar groups	Significant penalty (~8 kcal/mol for polar groups)
Favorable Entropy (-TΔS)	Hydrophobic effect, Desolvation entropy	Easier to optimize via hydrophobic group incorporation
Unfavorable Entropy	Configurational entropy loss, Conformational restriction	Loss of rotational, translational, and internal degrees of freedom

Case Studies in Drug Evolution: From First to Best-in-Class

HIV-1 Protease Inhibitors

The evolution of HIV-1 protease inhibitors provides a compelling illustration of thermodynamic optimization in drug development. Analysis of FDA-approved inhibitors reveals a clear thermodynamic trajectory from 1995 to 2006:

• Early inhibitors (1995-1996) exhibited binding affinities in the nanomolar range (Ki ≈ nM) with binding dominated by entropy, often accompanied by unfavorable or marginally favorable enthalpy [64].
• Later-generation inhibitors (2005-2006) achieved picomolar affinities (Ki ≈ pM) through substantially improved binding enthalpies. For instance, darunavir demonstrates a strongly favorable binding enthalpy of -12.7 kcal/mol [64].
• The transition to best-in-class status occurred over approximately ten years, with enthalpy optimization playing a decisive role in affinity enhancement.

Statins (HMG-CoA Reductase Inhibitors)

The cholesterol-lowering statin class demonstrates a parallel thermodynamic progression:

• First-generation compounds displayed characteristically entropy-driven binding profiles [64].
• Subsequent generations evolved toward more enthalpically favorable interactions, correlating with improved binding affinity [64].
• As with protease inhibitors, the thermodynamic refinement occurred over an extended period, suggesting systematic rather than serendipitous improvement.

Table 2: Thermodynamic Evolution of Drug Classes

Drug Class	First-in-Class Profile	Best-in-Class Profile	Affinity Improvement
HIV-1 Protease Inhibitors	Entropically driven, Unfavorable ΔH	Enthalpically optimized, ΔH = -12.7 kcal/mol (darunavir)	nM → pM (1000-fold)
Statins (HMG-CoA Reductase Inhibitors)	Entropically driven	Increased enthalpic contribution	Significant affinity increase
Thermodynamic Signature	-TΔS dominated	Balanced ΔH and -TΔS	Extreme affinity requires both

The consistent thermodynamic pattern across these diverse target classes suggests a fundamental principle: while first-in-class drugs can be discovered through entropic optimization, best-in-class status typically requires mastering enthalpic contributions.

The Critical Role of Configurational Entropy

Fundamentals of Configurational Entropy

Configurational entropy represents the entropy associated with the number of accessible conformational states available to a molecule or complex. Upon binding, both the drug molecule and target protein experience a significant loss of configurational entropy as their conformational space becomes restricted [3]. This entropy component is increasingly recognized as a major determinant in binding affinity and specificity.

Key aspects of configurational entropy in molecular interactions include:

• Magnitude of Effect: Configurational entropy changes can contribute substantially to binding free energies. In the Tsg101/PTAP peptide system, the total first-order entropy penalty was approximately 14 kcal/mol—a substantial energy penalty that must be overcome by favorable interactions [3].
• Structural Relationships: Configurational entropy exhibits intricate structure-entropy relationships, with different protein regions contributing disproportionately to the overall entropy change [3].
• Correlation Effects: Correlated motions between different degrees of freedom significantly influence configurational entropy, with pairwise correlations playing a major role in binding entropy changes [3].

Quantifying Configurational Entropy: The MIE Approach

The Mutual Information Expansion (MIE) method provides a systematic approach to computing configurational entropy changes from molecular dynamics simulations, accounting for correlated motions through mutual information terms [3]. The second-order MIE approximation incorporates pairwise correlations:

S ≈ S(2) ≡ ∑Si - ∑Iij

Where Si represents the entropy associated with variable i, and Iij is the mutual information between coordinates i and j, defined as:

Iij ≡ Si + Sj - Sij

This approach has revealed that changes in pairwise correlation upon binding make a major contribution to the overall configurational entropy change, highlighting the importance of accounting for these correlations in accurate binding models [3].

Diagram 1: MIE Method Workflow (76 characters)

Methodologies for Thermodynamic Profiling

Experimental Determination of Binding Energetics

Isothermal Titration Calorimetry (ITC)

ITC serves as the gold standard for experimentally determining thermodynamic parameters of binding interactions in solution. The methodology provides direct measurements of ΔG, ΔH, and Ka, from which ΔS can be derived.

Protocol Details:

• Experimental Setup: A typical ITC experiment involves sequential injections of a concentrated ligand solution into a sample cell containing the macromolecular target, with continuous measurement of heat flow required to maintain constant temperature.

• Data Analysis: Integration of injection heat peaks followed by nonlinear curve fitting to a binding model yields the enthalpy change (ΔH), association constant (Ka), and binding stoichiometry (n).

• Derived Parameters: The binding free energy (ΔG) is calculated as ΔG = -RTlnKa, and the entropy change (ΔS) is derived as ΔS = (ΔH - ΔG)/T.

• Key Considerations: ITC measures the total entropy change but does not directly distinguish between configurational entropy and solvation entropy contributions [3].

Supplementary Experimental Approaches

• Neutron Scattering: Provides information about vibrational entropy changes through the vibrational density of states, offering insights into changes in vibrational entropy upon binding [3].
• NMR Spectroscopy: Generalized order parameters from NMR can be used to estimate changes in configurational entropy, though with limitations in comprehensive bond vector coverage and correlation assessment [3].

Computational Approaches for Configurational Entropy

Multiple Molecular Dynamics Simulations (MMDS)

MMDS involves running multiple independent molecular dynamics trajectories to adequately sample conformational space for entropy calculations.

Protocol Details:

• System Preparation: Construct simulation systems for free receptor, free ligand, and receptor-ligand complex with appropriate solvation and ionization.

• Sampling Protocol: Execute multiple microsecond-scale simulations (as employed in Tsg101/PTAP studies) to ensure adequate conformational sampling [3].

• Trajectory Analysis: Extract time series of conformational variables (torsions, angles) for entropy calculation.

Mutual Information Expansion Implementation

Protocol Details:

• Coordinate Selection: Define relevant conformational variables (typically torsion angles) for entropy calculation.

• Probability Distributions: Estimate univariate and bivariate probability distributions from MD trajectories using histogram or kernel density methods.

• Entropy Calculation: Compute individual entropy terms (Si) and pairwise mutual information terms (Iij) using the second-order MIE approximation [3].

• Change Calculation: Determine entropy changes upon binding as ΔS = Scomplex - (Sreceptor + Sligand).

Diagram 2: Entropy Measurement Methods (76 characters)

The Scientist's Toolkit: Essential Research Reagents and Methodologies

Table 3: Research Reagent Solutions for Thermodynamic Studies

Reagent/Method	Function	Application Context
Isothermal Titration Calorimeter	Direct measurement of binding ΔH, Ka, and ΔS	Experimental determination of thermodynamic signatures for drug candidates
High-Performance Computing Cluster	Execution of microsecond-scale MD simulations	Configurational entropy calculations via MIE and other computational approaches
Deuterated Solvents & NMR Tubes	Sample preparation for NMR dynamics studies	Estimation of configurational entropy via generalized order parameters
Molecular Dynamics Software (e.g., GROMACS, AMBER)	Simulation of biomolecular trajectories	Generation of conformational ensembles for entropy analysis
Stable Isotope-Labeled Proteins	Production of proteins for NMR studies	Site-specific resolution of protein dynamics and entropy changes
Thermodynamic Database Systems	Correlation of structural motifs with thermodynamic parameters	Structure-thermodynamic relationship analysis for rational design
ABR-238901	ABR-238901, MF:C11H9BrClN3O4S, MW:394.63 g/mol	Chemical Reagent
Trimethylamine oxide-15N	Trimethylamine oxide-15N, MF:C3H9NO, MW:76.10 g/mol	Chemical Reagent

Implementation Framework for Rational Thermodynamic Design

Integrated Thermodynamic Optimization Strategy

Successful implementation of thermodynamic principles in drug design requires a systematic approach:

• Early Thermodynamic Profiling: Incorporate ITC measurements from lead discovery through optimization to establish thermodynamic structure-activity relationships (T-SAR) [64].

• Structure-Entropy Analysis: Employ MIE or similar computational methods to identify regions of disproportionate configurational entropy loss, guiding structural modifications to minimize these penalties [3].

• Enthalpic Optimization Cycle: Iteratively engineer hydrogen bond networks and van der Waals contacts while monitoring enthalpy gains to ensure they translate to improved affinity without compensatory entropy losses [64].

• Solvation Management: Strategically incorporate polar groups only when precise geometry can be achieved, minimizing desolvation penalties while maximizing specific interactions.

Overcoming Enthalpy-Entropy Compensation

The ubiquitous phenomenon of enthalpy-entropy compensation represents a significant challenge in thermodynamic optimization. Strategic approaches include:

• Conformational Constraint: Pre-organize drug molecules in bioactive conformations to reduce the conformational entropy penalty upon binding [64].
• Targeted Flexibility: Identify regions where maintained flexibility can preserve entropy without compromising binding affinity.
• Water Displacement: Strategically design ligands to displace poorly organized water molecules from binding sites, gaining both enthalpic and entropic benefits.

The evolution from first-in-class to best-in-class inhibitors follows a demonstrable thermodynamic trajectory characterized by progressive enthalpic optimization. While pioneering drugs frequently rely on entropic drivers, primarily the hydrophobic effect, optimized successors achieve superior affinity through balanced thermodynamic signatures with strong enthalpic contributions. Configurational entropy, particularly when quantified through advanced computational approaches like Mutual Information Expansion, provides critical insights into the molecular determinants of binding affinity and specificity.

The integration of thermodynamic profiling with structural and computational analysis represents a paradigm shift in rational drug design. By explicitly addressing the enthalpic and entropic components of binding throughout the optimization process, researchers can accelerate the development of best-in-class therapeutics with optimal affinity, selectivity, and physicochemical properties. As computational methods for estimating configurational entropy continue to mature, their integration with experimental thermodynamics promises to further refine our ability to engineer optimal molecular interactions, potentially collapsing the traditional decade-long optimization timeline into a more efficient, predictive process.

The documented thermodynamic progression from first to best-in-class, observed across multiple drug classes, provides both a validation of this approach and a roadmap for future drug development efforts aimed at achieving optimal therapeutic agents from the outset.

Case Studies and Validation: S_conf in Successful Drug Design and Material Science

Human Immunodeficiency Virus type 1 (HIV-1) protease remains one of the most critical enzymatic targets in antiretroviral therapy. This homodimeric aspartic protease, consisting of 99 amino acids per monomer, is essential for viral maturation [65]. It cleaves the Gag and Gag-Pol polyproteins at specific sites to produce functional structural proteins and enzymes, including itself, through an autocatalytic process [66] [67]. The catalytic triad Asp25-Thr26-Gly27 facilitates peptide bond hydrolysis, while conformational changes governed by flaps, hinge, cantilever, and fulcrum regions transition the enzyme between open and closed states crucial for substrate binding and cleavage [65]. The critical importance of this enzyme in the viral life cycle has made it a prime target for structure-based drug design, resulting in ten FDA-approved protease inhibitors that have fundamentally transformed HIV/AIDS treatment [66] [65].

Despite these advances, the development of drug resistance poses a significant challenge to long-term treatment efficacy. HIV-1's high genetic diversity, driven by its rapid replication rate (approximately 10^10 virions daily), viral recombination, and the error-prone nature of reverse transcriptase (introducing up to 1 error per 2000 base incorporations), has led to numerous subtypes with distinct geographical distributions [66]. While subtype B predominates in developed countries and has been the primary focus of drug development, accounting for only 12% of global infections, subtype C is responsible for more than 50% of infections worldwide and exhibits distinct genetic and structural characteristics that impact drug susceptibility [66] [65]. This review examines how a decade of research has progressively uncovered the critical role of thermodynamic parameters, particularly configurational entropy, in optimizing protease inhibitors against evolving viral challenges.

The Thermodynamic Framework of Inhibitor Binding

Fundamental Energetic Considerations

The binding affinity between HIV-1 protease and its inhibitors is governed by the Gibbs free energy equation (ΔG = ΔH - TΔS), where ΔH represents enthalpy changes and TΔS accounts for entropic contributions [68]. Traditional drug design often overemphasized optimizing enthalpy through strong intermolecular interactions like hydrogen bonds and van der Waals forces, while neglecting the significant role of entropy. Configurational entropy, which quantifies the reduction in molecular flexibility upon binding, has emerged as a crucial factor in understanding and improving inhibitor efficacy [69].

The molecular mechanics Poisson-Boltzmann surface area (MM-PBSA) and molecular mechanics generalized Born surface area (MM-GBSA) methods have become widely employed for estimating binding free energies from molecular dynamics simulations [68]. These approaches decompose the binding free energy into components:

ΔG~bind~ = ΔG~vdW~ + ΔG~ele~ + ΔG~pol,sol~ + ΔG~nonpol,sol~ - TΔS~config~

where van der Waals (ΔG~vdW~) and electrostatic (ΔG~ele~) interactions represent the gas-phase enthalpy, polar and nonpolar solvation terms (ΔG~pol,sol~, ΔG~nonpol,sol~) account for desolvation penalties, and -TΔS~config~ represents the entropic penalty from reduced flexibility [68] [69]. This decomposition has revealed that drug resistance mutations often operate through unfavorable shifts in van der Waals interactions and configurational entropy rather than solely through direct steric interference [69].

Methodological Advances in Thermodynamic Calculations

Table 1: Computational Methods for Thermodynamic Analysis of HIV-1 Protease Inhibition

Method	Theoretical Basis	Entropy Treatment	Applications	Limitations
MM-PBSA/MM-GBSA [68] [69]	Molecular mechanics force fields with implicit solvation	Normal mode analysis or quasiharmonic approximation	Binding affinity estimation for inhibitor series	Sensitivity to simulation length and initial conditions
Free Energy Perturbation (FEP)	Alchemical transformation with explicit solvent	Included implicitly through ensemble sampling	High-precision relative binding affinities	Computationally intensive, limited to similar compounds
Thermodynamic Integration (TI)	Pathway integration between states	Included implicitly through ensemble sampling	Absolute binding free energies	High computational cost, complex setup
Fragment Molecular Orbital (FMO) [70]	Quantum mechanical partitioning into fragments	Not directly calculated, but interaction energies decomposed	Guide inhibitor design through electronic structure analysis	Requires molecular dynamics for conformational sampling
Machine Learning Regression [71]	Statistical learning from genotype-phenotype databases	Learned implicitly from data patterns	Rapid resistance prediction from sequence data	Black-box nature limits molecular insights

Recent investigations have demonstrated that neglecting changes in configurational entropy leads to fundamentally incomplete understanding of binding affinities and drug resistance mechanisms. For instance, analysis of the potent inhibitors KNI-10033 and KNI-10075 revealed that drug resistance in I50V and I84V mutants arises mainly from unfavorable shifts in van der Waals interactions and configurational entropy [69]. In the case of the PR(I50V)-KNI-10075 complex, increased polar solvation free energy further contributed to resistance. Comparative studies between different inhibitor classes have highlighted that although KNI-10033 and KNI-10075 exhibit more favorable intermolecular electrostatic and van der Waals interactions compared to darunavir, their binding affinities are similar due to less favorable polar solvation terms for the KNI inhibitors [69].

Experimental and Computational Methodologies

Binding Free Energy Calculation Protocols

The MM-PBSA and MM-GBSA methodologies follow specific computational workflows. These end-point free energy methods calculate the binding free energy using the equation:

ΔG~bind~ = ⟨G~complex~⟩ - ⟨G~enzyme~⟩ - ⟨G~ligand~⟩

where ⟨G~complex~⟩, ⟨G~enzyme~⟩, and ⟨G~ligand~⟩ represent the average Gibbs free energy for the complex, enzyme, and ligand, respectively [68]. The single trajectory approach is typically employed, where configurations of the free enzyme and ligand are extracted from simulations of the complex to improve convergence by canceling noisy terms describing internal energies.

The binding free energy can be decomposed as: ΔG~MMPB(GB)SA~ = ΔG~vdW~ + ΔG~ele~ + ΔG~pol,sol~ + ΔG~nonpol,sol~

The electrostatic solvation free energy (ΔG~pol,sol~) is computed using Poisson-Boltzmann or Generalized Born methods, while the nonpolar solvation component (ΔG~nonpol,sol~) is estimated from solvent-accessible surface area using the equation:

ΔG~nonpol,sol~ = γ × A + β

where A represents the surface area, γ is the surface tension (typically 0.0052-0.0072 kcal mol^-1 Å^-2), and β is an offset constant [68]. Normal mode analysis then provides estimates of the configurational entropy by computing harmonic frequencies from minimized snapshots along the trajectory.

Machine Learning Approaches for Resistance Prediction

Machine learning methods have emerged as powerful tools for predicting drug resistance from sequence data. Recent work has utilized random forest regression (RFR), support vector regression (SVR), and self-consistent regression (SCR) to predict quantitative resistance values (fold ratio) based on HIV-1 protease sequences [71]. The input descriptors are typically binary vectors indicating the presence or absence of specific peptide fragments in each amino acid sequence. For optimal performance, sequences are split into overlapping pentapeptide fragments with a two-residue overlap [71]. These models demonstrate reasonable predictive performance for most protease inhibitors (R² = 0.828-0.909), with the exception of tipranavir (R² = 0.642) [71].

Diagram 1: Thermodynamic Optimization Workflow for HIV-1 Protease Inhibitors. This workflow integrates computational and experimental approaches with continuous refinement based on thermodynamic parameters.

Advanced Structural Analysis Techniques

The Fragment Molecular Orbital (FMO) method has enhanced structure-based drug design by providing quantum mechanical insights into inhibitor-protease interactions. This approach partitions the system into fragments and calculates interaction energies in parallel, offering superior treatment of electronic effects like polarization, charge transfer, and halogen bonding compared to molecular mechanics [70]. The pair interaction energy decomposition analysis (PIEDA) yields detailed insights through the equation:

PIE = ΔE~IJ~^ES^ + ΔE~IJ~^CT+mix^ + ΔE~IJ~^DI^ + ΔE~IJ~^EX^ + ΔG~Sol~^PCM^

where terms represent electrostatic (ES), charge transfer with mixed (CT+mix), dispersion (DI), exchange-repulsion (EX), and solvation (Sol) contributions [70]. This method has guided the design of darunavir analogs with improved potency against resistant mutants.

Table 2: Research Reagent Solutions for Thermodynamic Studies of HIV-1 Protease

Reagent/Resource	Type	Function in Research	Key Features
Stanford HIVdb [71]	Database	Genotype-phenotype relationship data	Curated repository of HIV-1 sequences with drug resistance measurements
AMBER [68]	Software Suite	Molecular dynamics simulations and free energy calculations	Implements MM-PBSA/MM-GBSA with normal mode entropy estimates
GOLD [70]	Software	Molecular docking and virtual screening	Genetic algorithm for flexible ligand docking into protease active site
GAMESS [70]	Software	Quantum mechanical calculations	Performs FMO calculations for electronic structure analysis
PDB2PQR [70]	Web Server	Protein structure preparation	Assigns protonation states for protease residues including catalytic aspartates
Combined Analog generator Tool (CAT) [70]	Programming Tool	Combinatorial analog generation	Creates novel inhibitor analogs without requiring commercial software licenses

Configurational Entropy in Inhibitor Design

Quantifying Entropic Penalties

Configurational entropy represents a fundamental but often overlooked component in the binding free energy of HIV-1 protease inhibitors. This term (-TΔS~config~) quantifies the free energy penalty associated with the reduction in molecular flexibility when a ligand transitions from the unbound to bound state. Normal mode analysis of harmonic frequencies from minimized MD snapshots has revealed that entropic penalties can vary significantly across different inhibitor classes and contribute substantially to resistance mechanisms [68] [69].

Comparative studies of high-affinity preclinical inhibitors KNI-10033 and KNI-10075 demonstrated that drug resistance mutations such as I50V and I84V cause unfavorable shifts in both van der Waals interactions and configurational entropy [69]. In some cases, the entropic contribution to resistance was comparable to or greater than the enthalpic components. These findings directly contradict the common assumption that configurational entropy contributions are similar across related inhibitors and can therefore be neglected in relative binding affinity calculations.

Structural Determinants of Entropic Penalties

The structural features of HIV-1 protease inhibitors significantly influence their entropic penalties upon binding. Inhibitors with greater flexibility in the unbound state typically pay larger entropic penalties upon binding to the relatively rigid protease active site. Analysis of darunavir analogs has revealed that strategic introduction of rigidifying elements, particularly in the P2 ligand region, can reduce entropic penalties while maintaining favorable enthalpic interactions [72] [70].

The oxabicyclo[3.2.1]octanol-derived P2 ligands represent one successful approach to optimizing this balance. These stereochemically defined fused-polycyclic ligands interact specifically with residues in the S2 subsite while minimizing entropic costs through restricted conformational freedom [72]. Crystal structures of inhibitor-protease complexes confirm that these ligands maintain extensive van der Waals contacts with the protease flap regions while reducing the entropy loss that would accompany binding of more flexible ligands.

Diagram 2: Configurational Entropy Factors in Inhibitor Binding. This diagram illustrates how configurational entropy components influence binding affinity and strategies for their optimization through inhibitor design.

Subtype-Specific Thermodynamic Considerations

The Challenge of HIV-1 Subtype C

HIV-1 subtype C presents distinct thermodynamic challenges for protease inhibitor design. Naturally occurring polymorphisms in subtype C protease, including T12S, I15V, L19I, M36I, R41K, H69K, L89M, and I93L, alter the structural and dynamic properties of the enzyme compared to subtype B [66] [65]. These polymorphisms impact flap flexibility, hinge region dynamics, and active site accessibility, ultimately affecting inhibitor binding thermodynamics.

The South African HIV-1 subtype C protease (C-SA PR) serves as a representative consensus sequence for this predominant subtype [66]. Biochemical and structural studies have demonstrated that subtype C protease exhibits decreased drug susceptibility to several FDA-approved inhibitors, despite these drugs having been designed against subtype B [66]. This reduced efficacy stems from the structural and dynamic differences between subtypes, highlighting the need for broad-spectrum inhibitors or subtype-specific design approaches.

Mutational Resistance and Thermodynamic Compensation

Drug resistance mutations in HIV-1 protease frequently operate through thermodynamic compensation mechanisms. Rather than completely abolishing inhibitor binding, resistance mutations often introduce subtle structural changes that alter the balance of enthalpic and entropic contributions to binding [73] [69]. Common resistance pathways include:

• Active site mutations (e.g., D30N, V32I, G48V, I50V/L, V82A/T/F/S, I84V): Directly alter inhibitor-protein interactions, often reducing van der Waals contacts while increasing conformational flexibility [70] [69].
• Flap region mutations (e.g., M46I/L, G48V, I54V/M/L/A/T): Modify the flexibility and dynamics of the flap regions that cover the active site, impacting the entropic component of binding [73].
• Non-active site mutations (e.g., L10I/F/R/V, L33F, L63P, A71V/T/I, L90M): Introduce long-range structural perturbations that indirectly affect active site geometry and dynamics [73].

Molecular field analysis using techniques like MB-QSAR (Mutation-dependent Biomacromolecular Quantitative Structure-Activity Relationship) has revealed that steric effects contribute approximately 60% to resistance profiles, while electrostatic effects account for the remaining 40% [73]. This highlights the predominance of shape complementarity in determining binding affinity across protease variants.

Emerging Approaches and Future Directions

Novel Binding Sites and Inhibition Mechanisms

Recent research has identified alternative strategies for inhibiting HIV-1 protease that leverage thermodynamic principles beyond active site competition. Molecular dynamics simulations have revealed a transient druggable binding pocket at the dimer interface that appears during incomplete dimerization [74]. This cryptic pocket has a lifetime longer than 1 μs and displays favorable druggability features, presenting opportunities for inhibitors that capture the protease in an inactive conformation rather than competing directly with substrates in the active site [74].

The discovery that certain protease inhibitors, including darunavir and saquinavir, can effectively block the initial autocleavage step in Gag-Pol processing suggests additional inhibition mechanisms beyond mature protease targeting [67]. This initial autocleavage, which occurs in the embedded protease within Gag-Pol before mature protease release, represents a thermodynamically distinct process from subsequent trans-cleavage events and may be differentially susceptible to inhibition [67].

Machine Learning-Guided Thermodynamic Optimization

The integration of machine learning with thermodynamic profiling represents a promising future direction for protease inhibitor development. Recent studies have demonstrated that quantitative structure-activity relationship (QSAR) models incorporating both sequence and structural features can successfully predict resistance profiles across diverse protease variants [71] [73]. These approaches enable rapid assessment of candidate inhibitors against virtual mutant libraries, prioritizing compounds with robust thermodynamic profiles against current and anticipated resistance mutations.

Fragment-based drug design guided by FMO calculations offers another powerful approach for optimizing the enthalpic-entropic balance [70]. By systematically modifying chemical substructures and quantitatively assessing their contributions to binding energy components, researchers can rationally design inhibitors with improved thermodynamic profiles. The development of computational tools like the Combined Analog generator Tool (CAT) facilitates this process by enabling combinatorial exploration of chemical space without requiring commercial software licenses [70].

Over the past decade, thermodynamic optimization has emerged as a crucial paradigm in HIV-1 protease inhibitor design. The recognition that configurational entropy contributes significantly to binding affinities and resistance mechanisms has transformed design strategies from a purely structural perspective to a dynamic, energy-based approach. Advances in computational methods, including enhanced sampling molecular dynamics, FMO calculations, and machine learning, have provided unprecedented insights into the thermodynamic drivers of inhibition efficacy. As HIV-1 continues to evolve and diversify globally, particularly with the increasing prevalence of non-B subtypes, these thermodynamic principles will guide the development of next-generation protease inhibitors with robust activity against resistant variants. The integration of thermodynamic profiling throughout the drug design process represents a powerful strategy for overcoming the persistent challenge of antiviral resistance.

Statins, as competitive inhibitors of 3-hydroxy-3-methylglutaryl coenzyme A (HMG-CoA) reductase, constitute a primary pharmacologic therapy for hypercholesterolemia. The binding affinity of these drugs is governed by a complex interplay of thermodynamic forces. This whitepaper delineates the critical correlation between enhanced binding affinity and favorable binding enthalpy, drawing on inhibition kinetics and microcalorimetric analyses. We detail how the thermodynamic dissection of these interactions—partitioning the free energy into its enthalpic (hydrogen bonding, van der Waals interactions) and entropic (hydrophobic interactions, desolvation, configurational entropy) components—provides a superior framework for rational drug design. This approach offers a pathway to overcome the pervasive challenge of enthalpy-entropy compensation and enables the identification of interactions that are paramount for achieving high affinity and specificity against HMG-CoA reductase.

The noncovalent interaction between a drug and its biological target is governed by the Gibbs free energy of binding (ΔG), which dictates the binding affinity and is determined by the classic relationship: ΔG = ΔH - TΔS. The enthalpic component (ΔH) primarily originates from specific, direct interactions such as hydrogen bonds and van der Waals contacts between the drug and the protein. The entropic component (-TΔS) is more complex, deriving from changes in solvation (hydrophobic effect) and the configurational entropy of the solute molecules upon binding [75] [1].

Historically, the entropic contribution, particularly the hydrophobic effect, was often prioritized in drug optimization. However, an over-reliance on entropic gains can lead to non-specific binding and poor drug selectivity. A contemporary paradigm shift emphasizes the importance of enthalpic optimization for developing high-affinity, specific inhibitors [76]. The most potent inhibitors frequently exhibit strongly favorable binding enthalpy, as exemplified by the statin class of drugs. A comprehensive thermodynamic profile, which includes the dissection of configurational entropy, is thus essential for modern drug development, providing critical insights that transcend the limitations of a purely affinity-based (K(i)) view [75].

Thermodynamic Profiling of Statins

Quantitative Analysis of Binding Parameters

Isothermal Titration Calorimetry (ITC) provides a direct route to measure the binding enthalpy (ΔH) and, in a single experiment, determine the binding constant (K), from which the entire thermodynamic profile (ΔG and TΔS) can be derived. A seminal ITC study profiled a representative set of statins, revealing a clear correlation between binding affinity and binding enthalpy [75].

Table 1: Experimentally Determined Thermodynamic Parameters for Statin Binding to HMG-CoA Reductase at 25°C

Statin	Type	K(i) (nM)	ΔG (kcal/mol)	ΔH (kcal/mol)	-TΔS (kcal/mol)	Enthalpy Contribution (%)
Rosuvastatin	II	~2	-12.0	-9.3	-2.7	76%
Cerivastatin	II	~5	-11.5	-5.2	-6.3	45%
Atorvastatin	II	~8	-11.3	-2.4	-8.9	21%
Fluvastatin	II	~28	-10.4	-0.4	-10.0	4%
Pravastatin	I	~250	-9.4	~0.0	~-9.4	~0%

Data adapted from Carbonell & Freire, 2005 [75] [77]. K(i) values are approximations. The Enthalpy Contribution is calculated as (ΔH/ΔG) × 100%.

The data in Table 1 demonstrates that the most potent statins, such as rosuvastatin and cerivastatin, derive a significant portion of their binding energy from favorable enthalpy (ΔH < 0). In contrast, less potent statins like pravastatin and fluvastatin rely almost exclusively on entropic driving forces (-TΔS), which are typically associated with non-specific hydrophobic effects and desolvation [75].

Structural and Thermodynamic Interpretation

The thermodynamic signatures reveal distinct interaction profiles for different statins. The high enthalpic contribution of rosuvastatin suggests the formation of numerous strong, specific interactions—such as hydrogen bonds and van der Waals contacts—within the active site of HMG-CoA reductase. Conversely, the binding of pravastatin is predominantly entropically driven, indicating a binding process dominated by the hydrophobic effect and the release of water molecules, with minimal specific polar interactions [75].

This thermodynamic dissection underscores that the balance of molecular interactions is not identical across all statins. The progression towards higher potency is linked to the successful incorporation of enthalpically favorable interactions, moving beyond a reliance on hydrophobic and desolvation effects alone. This principle provides a blueprint for the rational design of next-generation inhibitors.

Experimental Protocols for Thermodynamic Analysis

Isothermal Titration Calorimetry (ITC) for Enthalpy Determination

Objective: To directly measure the binding enthalpy (ΔH), stoichiometry (n), and association constant (Ka) of a statin binding to HMG-CoA reductase.

Methodology:

• Sample Preparation: Purified HMG-CoA reductase protein is dialyzed extensively into a suitable buffer (e.g., phosphate buffer, pH 7.0). The statin inhibitor is dissolved in the final dialysate to ensure perfect chemical matching and avoid heat effects from dilution or mixing.
• Instrument Setup: The ITC instrument is equilibrated at the desired temperature (e.g., 25°C). The protein solution is loaded into the sample cell, and the statin solution is loaded into the syringe.
• Titration Experiment: A typical experiment involves a series of sequential injections (e.g., 25 injections of 2 µL each) of the statin solution into the protein cell, with constant stirring. The instrument measures the heat flow (microcalories per second) required to maintain a constant temperature difference (with the reference cell) after each injection.
• Data Analysis: The raw heat pulses per injection are integrated and plotted as a function of the molar ratio of statin to protein. This isotherm is then fit to a suitable binding model (e.g., a single-set-of-sites model) using nonlinear regression to extract ΔH, n, and Ka. The Gibbs free energy (ΔG) and the entropic component (-TΔS) are calculated using the relationships: ΔG = -RTln(Ka) and -TΔS = ΔG - ΔH [75].

Enzyme Inhibition Kinetics for Affinity Constant (K(i)) Determination

Objective: To determine the inhibition constant (K(i)), which quantifies the potency of a statin.

Methodology:

• Assay Configuration: The activity of HMG-CoA reductase is measured by monitoring the oxidation of NADPH to NADP+, which results in a decrease in absorbance at 340 nm. The assay mixture contains the enzyme, substrate (HMG-CoA), cofactor (NADPH), and buffer.
• IC50 Determination: The initial reaction velocity is measured at a fixed substrate concentration in the presence of varying concentrations of the statin inhibitor. The concentration of inhibitor that reduces the enzyme activity by 50% (IC50) is determined from a plot of activity versus inhibitor concentration.
• K(i) Calculation: The IC50 value is converted to the inhibition constant K(i) using the Cheng-Prusoff equation for competitive inhibitors: K(i) = IC50 / (1 + [S]/K(m)), where [S] is the substrate concentration and K(m) is the Michaelis constant for HMG-CoA [75].

Visualizing the Thermodynamic and Experimental Framework

The following diagrams illustrate the core concepts and methodologies discussed in this whitepaper.

Diagram 1: Thermodynamic and experimental framework for statin binding.

Diagram 2: ITC experimental workflow for binding measurement.

The Scientist's Toolkit: Essential Research Reagents & Materials

Successful thermodynamic profiling of statin binding requires specific reagents and instrumentation. The following table details key solutions and materials used in the featured experiments.

Table 2: Essential Research Reagents and Materials for Thermodynamic Binding Studies

Reagent / Material	Function / Description	Example from Statin Research
Purified HMG-CoA Reductase	The target enzyme. Catalytic domain is often used for in vitro studies. Source can be recombinant human protein expressed in E. coli or other systems.	Essential for all binding and inhibition assays [75].
Statin Analytes	The inhibitors under investigation. Must be of high purity (>95%). Both type I (e.g., pravastatin) and type II (e.g., rosuvastatin) statins are critical for comparative studies.	Pravastatin, fluvastatin, cerivastatin, atorvastatin, rosuvastatin [75] [77].
Isothermal Titration Calorimeter (ITC)	The core instrument for directly measuring binding enthalpy (ΔH), affinity (Ka), and stoichiometry (n) in a single experiment.	MicroCal ITC instruments are commonly used [75] [76].
UV-Visible Spectrophotometer	For monitoring NADPH consumption in enzyme activity and inhibition assays (measurement at 340 nm).	Used for determining IC50 values in kinetic assays [75].
Chromatography Buffers & Immobilized Artificial Membranes (IAM)	To study statin-membrane interactions and passive permeability, which influences pharmacokinetics and pleiotropic effects.	Phosphatidylcholine monolayers immobilized on silica (e.g., IAM columns) [78].
Dialysis Cassettes/Buffers	For exhaustive buffer exchange to ensure perfect chemical matching between protein and ligand samples, a critical prerequisite for accurate ITC data.	Used in sample preparation for ITC to minimize heat of dilution artifacts [75].
IPS-06061	IPS-06061, MF:C22H26O3, MW:338.4 g/mol	Chemical Reagent
Folate-MS432	Folate-MS432, MF:C50H65F3IN7O6S, MW:1076.1 g/mol	Chemical Reagent

The thermodynamic profiling of statins reveals a definitive correlation: the most potent inhibitors of HMG-CoA reductase are those with the strongest favorable binding enthalpy. While entropic forces driven by hydrophobicity are a significant contributor to binding for many statins, the optimization of enthalpic contributions—through the strategic introduction of specific hydrogen bonds and van der Waals interactions—is the hallmark of superior affinity and specificity.

This enthalpy-driven approach provides a robust strategy to circumvent the common pitfall of enthalpy-entropy compensation in drug design. By utilizing experimental techniques like ITC to obtain full thermodynamic profiles, researchers can move beyond simplistic affinity metrics. This enables a deeper understanding of the molecular interactions governing binding, guiding the rational design of next-generation therapeutic inhibitors with optimized efficacy and reduced off-target effects. Integrating this with an understanding of broader properties, such as configurational entropy and membrane interactions, paves the way for truly predictive and robust drug development.

The pursuit of advanced energy storage systems has catalyzed innovation in solid-state battery technology, with solid polymer electrolytes (SPEs) emerging as a cornerstone material due to their excellent processability, flexibility, and enhanced safety profiles. However, the practical application of SPEs has been persistently challenged by a fundamental trade-off between high ionic conductivity and robust mechanical strength [79]. Conventional SPEs, such as poly(ethylene oxide) (PEO)-based systems, typically suffer from low ionic conductivity at room temperature (often <10⁻⁵ S cm⁻¹), necessitating elevated operational temperatures that compromise battery safety and energy efficiency [80]. Recently, the novel paradigm of high-entropy design—originally pioneered in metallurgy with high-entropy alloys—has been strategically adapted to electrolyte engineering, offering a transformative approach to overcoming these historical limitations [81] [82].

High-entropy solid polymer electrolytes (HE-SPEs) leverage the thermodynamic principle of configurational entropy to create materials with exceptional structural disorder and functional synergy. The foundational concept rests upon the Gibbs free energy equation (ΔG = ΔH – TΔS), wherein an increase in configurational entropy (ΔS) can stabilize otherwise metastable phases and induce favorable local structural evolution [83] [84]. In polymeric systems, this is achieved by incorporating multiple, functionally diverse molecular or ionic constituents in near-equimolar ratios, thereby maximizing the entropy of mixing. The resulting materials exhibit four characteristic effects: the high-entropy effect, which stabilizes the disordered structure; the lattice distortion effect (in crystalline regions) or free volume effect (in amorphous domains), which creates novel ion transport pathways; the sluggish diffusion effect, which inhibits deleterious phase separation; and the cocktail effect, where synergistic interactions between components produce emergent properties unattainable by any single constituent [80] [84] [82]. For researchers investigating intermolecular interactions, HE-SPEs represent a model system where entropy-driven modulation of molecular assembly—such as the disruption of ion clusters and suppression of polymer crystallinity—directly governs macroscopic electrochemical and mechanical performance [85]. This whitepaper delineates the mechanistic role of configurational entropy in HE-SPEs, provides quantitative performance comparisons, details experimental methodologies, and visualizes the underlying design principles enabling their exceptional functionality.

Performance Advantages and Quantitative Metrics

The strategic introduction of high-entropy configurations into SPEs has yielded remarkable improvements in key electrochemical and mechanical properties, effectively resolving the classic conductivity-mechanical integrity dilemma. Quantitative data extracted from recent pioneering studies unequivocally demonstrates the performance superiority of HE-SPEs across multiple metrics critical for room-temperature solid-state lithium metal batteries.

Table 1: Comparative Electrochemical Performance of HE-SPEs vs. Traditional Electrolytes

Electrolyte Type	Ionic Conductivity (S cm⁻¹)	Li⁺ Transference Number	Electrochemical Window (V)	Mechanical Strength	Reference
HE-SPE (HESZ-SPE)	4.60 × 10⁻³ at 25°C	0.86	>5.0	Excellent	[79]
PEO-based SPE	<10⁻⁵ at 25°C	~0.2	~4.0	Poor (Young's modulus <1 MPa)	[80]
In-Situ Polymerized HE-SPE (IWSWN-SPE)	4.32 × 10⁻⁴ at 25°C	0.70	5.15	Superior (free-standing)	[86]
High-Entropy Multi-Salt Liquid Electrolyte	1.21 × 10⁻² at 25°C	N/A	N/A	N/A	[80]

The performance enhancements extend beyond room-temperature operation. A notable entropy-driven SPE demonstrated an 8.5-fold improvement in ionic conductivity at -20°C (0.17 mS cm⁻¹) compared to its low-entropy counterpart, alongside a 2-fold reduction in Li⁺ cluster size that facilitates rapid ion desolvation [85]. This exceptional low-temperature performance is attributed to entropy-mediated suppression of polymer crystallization and more uniform ion distribution. Furthermore, HE-SPEs exhibit exceptional interfacial stability, with Li/Li symmetric cells maintaining stable plating/stripping for over 2500 hours at 0.2 mA cm⁻² [86] and other high-entropy polymer systems exceeding 4000 hours cycle life [80]. The transference number—a crucial parameter indicating the fraction of current carried by Li⁺ ions—reaches exceptionally high values of 0.86 in zwitterionic HE-SPE designs [79], substantially exceeding the ~0.2-0.3 typical of PEO-based electrolytes and mitigating concentration polarization during high-rate cycling.

Table 2: Application Performance of HE-SPEs in Functional Battery Systems

Battery Configuration	Cycling Performance	Temperature Conditions	Key Advancements	Reference
Li|HE-SPE|NCM622	300 cycles stable cycling	30°C	High mass loading (15.8 mg cm⁻²) compatible	[86]
Li|HE-SPE|LFP	120 cycles stable cycling	100°C	Exceptional high-temperature stability	[86]
Li|HE-SPE|LFP	91.49% capacity retention after 500 cycles	-20°C	13-fold capacity improvement at low temperature	[85]
2.6-Ah Pouch Cell (Li|HE-SPE|NCM811)	349 Wh kg⁻¹ specific energy	Room temperature	Validated practical application potential	[86]

Experimental Protocols and Methodologies

In Situ Polymerization Synthesis of HE-SPEs

The synthesis of high-performance HE-SPEs typically employs in situ polymerization techniques, which facilitate excellent electrode-electrolyte contact and are compatible with conventional battery manufacturing processes. A representative protocol for creating a high-entropy supramolecular zwitterion solid polymer electrolyte (HESZ-SPE) involves the following steps [79]:

• Precursor Solution Preparation: Dissolve multiple functional monomers (e.g., vinyl ethylene carbonate, zwitterionic species, and other allyl/methacrylate derivatives) in a suitable solvent with a lithium salt (e.g., LiTFSI). The monomer selection should promote diverse molecular interactions, including hydrogen bonding and dipole-dipole interactions, to create a high-entropy supramolecular network.
• Initiation System Addition: Introduce a thermal initiator (e.g., azobisisobutyronitrile) at concentrations typically ranging from 0.5-2 wt% relative to the total monomer content.
• Cell Assembly and Curing: Inject the precursor solution into pre-assembled battery cells (e.g., Li\|electrode cells) and subsequently heat the assembly to 60-80°C for 4-12 hours to complete the free-radical polymerization directly within the cell configuration.
• Post-polymerization Characterization: Validate successful polymerization and compositional uniformity using techniques such as solid-state nuclear magnetic resonance (ssNMR), particularly ¹⁹F and ³¹P NMR, to confirm incorporation of all designed functional segments [86].

Puzzle-Like Molecular Assembly Strategy

An advanced synthetic approach termed "puzzle-like molecular assembly" enables precise integration of distinct functional segments into a unified polymer matrix [86]:

• Monomer Selection: Choose three primary monomeric building blocks with complementary functionalities:
  • Vinyl ethylene carbonate: Provides strong Li⁺ coordination and ion transport channels.
  • Fluorinated methacrylate: Enhances oxidation stability and facilitates formation of a robust solid electrolyte interphase.
  • Phosphorus-containing monomer: Imparts flame retardancy and improves lithium salt dissociation.
• Free-Radical Copolymerization: Conduct polymerization under inert atmosphere using a radical initiator, allowing the different monomers to copolymerize into a random, high-entropy network.
• Structural Validation: Employ Fourier-transform infrared spectroscopy to monitor the disappearance of C=C stretching vibrations, confirming successful polymerization, and X-ray photoelectron spectroscopy to verify the presence and distribution of key heteroatoms.

Entropy-Driven Modulation of Polymer Crystallinity

To specifically enhance low-temperature performance, a multicomponent strategy focused on entropy-driven modulation of polymer crystallinity and ion clustering has been developed [85]:

• Multi-salt/Multi-monomer Formulation: Incorporate at least three different lithium salts and multiple polymerizable monomers in equimolar or near-equimolar ratios to maximize configurational entropy.
• Crystallinity Suppression: The high-entropy composition inherently disrupts long-range polymer ordering, reducing crystallinity as quantified by differential scanning calorimetry.
• Ion Cluster Reduction: Utilize small-angle X-ray scattering to demonstrate a 2-fold reduction in Li⁺ cluster size compared to low-entropy controls, facilitating improved ion transport.
• Electrochemical Validation: Assemble Li/Cu half-cells to measure Coulombic efficiency and Li/LiFePOâ‚„ full cells to assess capacity retention at temperatures as low as -20°C.

The Scientist's Toolkit: Essential Research Reagents

The development and investigation of HE-SPEs require specific materials and characterization tools to effectively manipulate configurational entropy and analyze its effects. The following table catalogues essential research reagents and their functions in this emerging field.

Table 3: Essential Research Reagents and Materials for HE-SPE Development

Material/Reagent Category	Specific Examples	Function in HE-SPE	Research Consideration
Functional Monomers	Vinyl ethylene carbonate, zwitterionic monomers, allyl phosphates, fluorinated methacrylates	Creates diverse coordination environments, introduces specific functionalities, maximizes configurational entropy	Prioritize monomers with complementary coordination strengths and chemical functionalities
Lithium Salts	LiTFSI, LiFSI, LiDFOB, LiNO₃, LiPF₆	Provides Li⁺ ions for conduction, different anions influence dissociation and interphase formation	Multi-salt formulations enhance entropy and exploit synergistic effects; monitor solubility limits
Polymerization Initiators	Azobisisobutyronitrile, benzoyl peroxide	Initiates free-radical polymerization for in situ formation of HE-SPEs	Optimize concentration and decomposition temperature for complete conversion
Mechanical Reinforcements	Al₂O₃-coated polyethylene separators, ceramic nanoparticles (LLZO, TiO₂)	Provides mechanical scaffold, suppresses dendrite penetration, enhances thermal stability	Ensure homogeneous distribution to maintain uniform ion transport
Characterization Tools	Solid-state NMR, EIS, XPS, SAXS, DSC	Quantifies entropy effects, measures ionic conductivity, analyzes interphase composition, assesses crystallinity	Combine multiple techniques to establish structure-property relationships
Succinate dehydrogenase-IN-3	Succinate dehydrogenase-IN-3, MF:C20H15ClF2N4OS2, MW:464.9 g/mol	Chemical Reagent	Bench Chemicals
C12-iE-DAP	C12-iE-DAP, MF:C12H21N3O7, MW:319.31 g/mol	Chemical Reagent	Bench Chemicals

Visualization of HE-SPE Design Principles and Workflows

High-Entropy SPE Mechanism

HE-SPE Experimental Workflow

High-entropy solid polymer electrolytes represent a paradigm shift in solid-state battery design, where configurational entropy is strategically harnessed to optimize intermolecular interactions and overcome historical material limitations. The documented performance metrics—including ionic conductivities exceeding 10⁻³ S cm⁻¹ at room temperature, Li⁺ transference numbers approaching 0.9, and exceptional stability across extreme temperatures—demonstrate the profound impact of entropy-driven design on electrochemical functionality [79] [85] [86]. The experimental protocols and visualization frameworks presented herein provide researchers with comprehensive methodologies for synthesizing and characterizing these advanced materials systems.

Future research should prioritize establishing quantitative structure-entropy-property relationships through advanced computational modeling and in situ characterization techniques. Particular focus should be directed toward standardizing entropy calculation methods across polymeric systems, where configurational, vibrational, and conformational entropy all contribute to the overall entropy landscape [81]. Additionally, scaling synthesis protocols for commercial production while managing raw material complexity presents an important engineering challenge. Machine learning-assisted composition optimization and active learning frameworks show exceptional promise for navigating the vast high-entropy design space efficiently [82]. As the fundamental understanding of entropy-structure-property relationships in polymer electrolytes matures, HE-SPEs are poised to enable the next generation of safe, high-energy-density batteries capable of operation under extreme conditions, marking a significant advancement in both energy storage technology and the applied science of intermolecular interactions.

Intermolecular interactions research has traditionally relied on pairwise additive models, but a paradigm shift is occurring with the recognition that multi-body effects fundamentally reshape thermodynamic behavior through non-additive entropy. This technical analysis demonstrates how configurational entropy, particularly through correlated motions and many-particle interactions, necessitates advanced modeling frameworks beyond mean-field approximations. We examine how lattice gas models, cluster expansion methods, and mutual information approaches quantitatively capture these effects, enabling accurate prediction of phase diagrams for alloys, high-entropy materials, and biological systems. The integration of these computational methodologies with experimental validation provides a comprehensive toolkit for researchers investigating complex interactions in drug development and materials design, where neglecting multi-body entropy contributions can lead to qualitatively incorrect predictions of phase stability and binding behavior.

Configurational entropy represents a fundamental thermodynamic quantity measuring the number of distinct atomic or molecular arrangements accessible to a system at a given temperature. Within the context of intermolecular interactions research, understanding configurational entropy is essential for predicting binding affinities, phase stability, and material properties. Traditional models often treat entropy as an additive quantity, where total system entropy equals the sum of individual contributions from independent components. However, correlated motions and multi-body interactions create non-additive effects that fundamentally alter thermodynamic behavior [3].

When particles interact, their motions become correlated, creating entropic contributions that cannot be captured by simple summation of individual components. These non-additive effects manifest prominently in diverse systems: protein-ligand complexes where binding entropy depends on correlated fluctuations [3], high-entropy alloys where multi-component interactions stabilize solid solutions [87], and metallic systems where vibrational and configurational entropy combine to determine phase boundaries [88]. In each case, neglecting these multi-body entropy contributions leads to qualitatively incorrect predictions of phase stability and binding behavior.

This technical guide establishes a comprehensive framework for analyzing non-additive entropy effects, with particular emphasis on methodologies relevant to drug development professionals and materials researchers. By integrating theoretical models, computational approaches, and experimental validation techniques, we provide a foundation for accurately capturing how multi-body interactions reshape entropy and phase diagrams across chemical and biological systems.

Theoretical Foundations of Non-Additive Entropy

Basic Entropy Formulations

In statistical mechanics, entropy fundamentally measures the uncertainty associated with a system's microscopic states. The Boltzmann-Gibbs entropy formula represents the classical approach:

[ S = -kB \sumi pi \ln pi ]

where ( kB ) is Boltzmann's constant and ( pi ) represents the probability of microstate ( i ). This formulation assumes weak correlations between system components, making entropy extensive and additive [89]. However, for systems with strong correlations and long-range interactions, this additivity breaks down, necessitating generalized entropy formulations.

Non-additive entropy forms have been developed to address these limitations, with the Tsallis entropy representing a prominent example:

[ Sq = \frac{kB}{q-1} \left( 1 - \sumi pi^q \right) ]

where ( q ) is a parameter quantifying the degree of non-extensivity [89]. This formulation has found applications in systems with non-trivial correlations, including complex biological systems, non-equilibrium processes, and multi-component materials. The distinguishing feature of these generalized entropies is their non-additivity under the combination of independent systems, directly capturing the multi-body effects that emerge from correlated fluctuations.

Configurational Entropy and Correlation

Configurational entropy specifically measures the contribution from different spatial arrangements of atoms or molecules. In solid-state materials, this includes the distinct ways lattice sites can be occupied at specific concentrations [90]. For protein-ligand systems, it encompasses the various conformational states accessible to the molecules [3].

The mutual information expansion (MIE) provides a systematic framework for quantifying how correlations affect configurational entropy. The second-order MIE approximation accounts for pairwise correlations:

[ S \approx S^{(2)} \equiv \sumi^N Si - \sum{j>i}^N I{ij} ]

where ( Si ) is the entropy associated with variable ( i ), and ( I{ij} ) is the mutual information between coordinates ( i ) and ( j ) [3]. The mutual information term:

[ I{ij} \equiv Si + Sj - S{ij} ]

where ( S_{ij} ) is the joint entropy of variables ( i ) and ( j ), directly captures the non-additive reduction in entropy due to correlations between degrees of freedom. This approach has revealed that changes in pairwise correlation contribute significantly to entropy changes during biomolecular binding, with important implications for drug design where entropy-enthalpy compensation often determines binding specificity and affinity [3].

Computational Methodologies

Lattice Gas Models for Phase Behavior

Lattice gas models provide a powerful statistical framework for analyzing atomic distribution, phase stability, and segregation in multi-component systems. By representing atoms on discrete lattice sites and considering their interactions, these models predict both equilibrium and non-equilibrium states, effectively revealing the entropic and enthalpic drivers behind phase transitions [87].

In these models, the system Hamiltonian incorporates both single-particle energies and pairwise or multi-body interactions:

[ H = \sumi \varepsiloni ni + \sum{i{ij} ni nj + \sum{i{ijk} ni nj nk + \cdots ]}>

where ( ni ) represents occupation numbers, ( \varepsiloni ) are site energies, ( V{ij} ) are pairwise interactions, and ( V{ijk} ) represent three-body interactions that capture non-additive effects [87]. The inclusion of three-body and higher terms is essential for accurately modeling systems where the interaction between two particles is modulated by the presence of a third.

These models have proven particularly valuable for studying high-entropy alloys (HEAs), where the presence of five or more principal elements in near-equimolar ratios leads to high configurational entropy that promotes the formation of solid solution phases with enhanced mechanical properties, thermal stability, and corrosion resistance [87]. Lattice gas models enable accurate modeling of atomic interactions, phase segregation, and order-disorder transformations in these complex systems.

Table 1: Comparison of Classical and Quantum Lattice Gas Models

Aspect	Classical Lattice Gas	Quantum Lattice Gas
Computational Complexity	O(N)—Linear Complexity	O(log N)—Logarithmic Complexity
Scaling Behavior	Scales linearly with system size	Scales logarithmically with system size
Key Advantage	Simple, well-studied for fluid dynamics	Massive speedup for large simulations
Limitation	Limited scalability; high computational cost	Requires advanced quantum hardware; noise-sensitive
Applications	Computational fluid dynamics, turbulence modeling	Quantum fluid dynamics, quantum field theory

Cluster Expansion Method

The cluster expansion (CE) method provides a numerically efficient approach for evaluating the energies of numerous configurational states of a specific lattice. This technique represents the energy of a configuration as a sum of contributions from clusters of sites:

[ E(\sigma) = J0 + \sum{\alpha} J{\alpha} \Phi{\alpha}(\sigma) ]

where ( \sigma ) represents a specific configuration, ( J0 ) is the energy of a reference configuration, ( J{\alpha} ) are effective cluster interactions (ECI), and ( \Phi_{\alpha}(\sigma) are correlation functions for cluster ( \alpha ) [88] [90]. The CE method has been widely used in calculating the thermodynamic properties of alloys because it requires only a handful of initial DFT calculations (typically <100) for training the model, yet can accurately predict energies for practically all configurational states [90].

This approach has been successfully applied to predict complete phase diagrams, as demonstrated in first-principles predictions of the Al-Li phase diagram including both configurational and vibrational entropic contributions [88]. The study found excellent agreement with experimental phase diagrams, accurately capturing the stability of various phases (AlLi, Al2Li3, AlLi2, Al4Li9) and metastable phases (Al3Li), as well as phase boundaries and maximum stability temperatures [88].

Mutual Information Expansion (MIE) for Biomolecular Systems

The mutual information expansion (MIE) offers a systematic approach to computing configurational entropy changes from molecular simulations, accounting for both linear and nonlinear correlations between degrees of freedom [3]. This method is particularly valuable for studying protein-ligand binding, where it has revealed that correlated motions contribute significantly to entropy changes during association.

In application to the UEV domain of Tsg101 binding an HIV-derived peptide, MIE analysis demonstrated that the total first-order entropy loss (neglecting correlations) would impose a free energy penalty of approximately 14 kcal mol(^{-1}), with most of this change (12 kcal mol(^{-1})) coming from reduced motion of the protein rather than the peptide ligand [3]. However, inclusion of pairwise correlation effects through the second-order MIE approximation significantly modified this picture, highlighting the importance of non-additive contributions.

Table 2: First-Order Entropy Changes in Protein-Peptide Binding

Component	Entropy Change (kcal mol(^{-1}))	Percentage of Total
Tsg101 Protein	-12.0	85.7%
PTAP Peptide	-2.0	14.3%
Torsional DOF	-12.0	85.7%
Angular DOF	-1.5	10.7%
Bond DOF	-0.5	3.6%

Experimental Protocols and Validation

First-Principles Phase Diagram Prediction

Protocol Objective: Prediction of phase diagrams from first principles calculations incorporating configurational and vibrational entropy.

Methodology:

• Cluster Expansion Construction:
  • Generate multiple atomic configurations for the system of interest
  • Calculate formation enthalpies using density functional theory (DFT)
  • Fit cluster expansion Hamiltonian to DFT-calculated energies
  • Validate CE model against held-out DFT calculations [88]

• Vibrational Entropy Incorporation:

  • Determine bond length vs. bond stiffness relationships for each bond type
  • Calculate vibrational entropic contributions for each configuration
  • Integrate vibrational entropy into Gibbs free energy calculations [88]

• Monte Carlo Simulations:

  • Perform Monte Carlo simulations at varying temperatures
  • Calculate Gibbs free energy as a function of temperature
  • Determine phase boundaries from free energy minimization [88]

Validation: Compare predicted phase diagram with experimentally determined phase boundaries, stable phases (e.g., AlLi, Al2Li3, AlLi2, Al4Li9), and metastable phases (e.g., Al3Li) [88].

Protein-Ligand Binding Entropy Analysis

Protocol Objective: Quantification of configurational entropy changes during protein-ligand binding using mutual information expansion.

Methodology:

• Molecular Dynamics Simulations:
  • Perform multiple microsecond-scale MD simulations of free receptor and ligand
  • Perform equivalent simulations of bound complex
  • Ensure adequate sampling of conformational space [3]

• Entropy Calculation:

  • Define conformational variables (bond lengths, angles, torsions)
  • Calculate probability distribution functions for each variable
  • Compute individual entropy terms for each variable
  • Calculate pairwise mutual information terms [3]

• MIE Implementation:

  • Apply second-order MIE approximation including all pairs of degrees of freedom
  • Compute entropy changes for receptor, ligand, and complex
  • Analyze contributions from changes in individual terms and correlation terms [3]

Validation: Compare computed entropy changes with experimental binding affinities, focusing on the role of entropy-enthalpy compensation in determining binding specificity.

Case Studies and Applications

Metallic Alloys: Al-Li System

The Al-Li system demonstrates how incorporating both configurational and vibrational entropy enables accurate phase diagram prediction. First-principles calculations combined with cluster expansion and Monte Carlo simulations successfully predicted the complete phase diagram, including the stability ranges for intermetallic compounds AlLi, Al2Li3, AlLi2, and Al4Li9 [88]. This approach accurately captured the phase boundaries between different compounds and the maximum stability temperature of line compounds.

Crucially, the study revealed that vibrational entropy significantly influences phase stability at elevated temperatures, demonstrating that accurate prediction requires going beyond simple configurational entropy models [88]. The methodology provided precise information about the gap between Al3Li and AlLi solvus lines, highlighting the importance of non-additive effects in determining phase coexistence regions.

High-Entropy Alloys

High-entropy alloys (HEAs) represent a novel class of metallic materials composed of five or more principal elements in near-equimolar ratios, where high configurational entropy promotes the formation of solid solution phases rather than intermetallic compounds [87]. The unconventional composition leads to enhanced mechanical properties, thermal stability, and corrosion resistance.

In HEAs, phase stability plays a critical role in determining structural integrity and performance. Lattice gas models have proven effective in predicting phase behavior, including order-disorder transformations, precipitation hardening, and phase decomposition [87]. The combination of computational simulations (Monte Carlo, molecular dynamics) with experimental validation (XRD, TEM, APT) has improved predictive accuracy for these complex systems.

Recent advances have incorporated data-driven methodologies and machine learning for high-throughput exploration of HEA compositions, accelerating the discovery of alloys with optimized phase stability and superior mechanical performance [87]. These approaches effectively capture the non-additive multi-body interactions that determine phase stability in these complex systems.

Biomolecular Recognition: Tsg101-PTAP System

Application of the mutual information expansion to the binding of the Tsg101 UEV domain with an HIV-derived PTAP peptide revealed intricate structure-entropy relationships [3]. The computed change in configurational entropy was large and found to have a major contribution from changes in pairwise correlation, demonstrating that accurate binding models must carefully account for configurational entropy changes.

The analysis showed that entropy changes were distributed asymmetrically between the protein and peptide, with Tsg101 contributing approximately 85% of the total entropy loss [3]. This asymmetry reflects how binding-induced rigidification propagates through the protein structure, creating long-range correlations that contribute non-additively to the overall entropy change. These findings have implications for drug design targeting Tsg101 to inhibit HIV budding.

Research Reagent Solutions

Table 3: Essential Computational Tools for Analyzing Non-Additive Entropy

Tool/Method	Function	Application Examples
Cluster Expansion (CE)	Numerically efficient evaluation of configurational energies	Phase diagram prediction for metallic alloys [88] [90]
Lattice Gas Models	Statistical framework for atomic distribution and phase stability	Modeling order-disorder transitions in HEAs [87]
Mutual Information Expansion (MIE)	Computation of configurational entropy accounting for correlations	Protein-ligand binding entropy analysis [3]
Monte Carlo Simulations	Sampling of configurational space	Thermodynamic property calculation [88] [87]
Density Functional Theory (DFT)	First-principles energy calculations	Training data for cluster expansion [88] [90]

The analysis of non-additive interactions through advanced computational methodologies has fundamentally transformed our understanding of how multi-body effects reshape entropy and phase diagrams across diverse systems. From metallic alloys to biomolecular complexes, the recognition that configurational entropy contains significant non-additive contributions from correlated motions has necessitated a paradigm shift in thermodynamic modeling.

The integration of lattice gas models, cluster expansion techniques, and mutual information approaches provides a comprehensive toolkit for capturing these effects, enabling accurate prediction of phase behavior in complex, multi-component systems. For researchers in drug development and materials design, incorporating these non-additive entropy contributions is essential for predicting binding affinities, phase stability, and material properties with quantitative accuracy.

As computational power increases and methodologies continue to refine, the ability to capture increasingly subtle correlation effects will further enhance our understanding of how multi-body interactions shape thermodynamic behavior across chemical, materials, and biological systems.

Diagram: Workflow for Phase Diagram Prediction

The accurate prediction of binding affinity is a central challenge in computational biophysics and structure-based drug design. The process of biomolecular binding is governed by the fundamental equation of thermodynamics, where the binding free energy (ΔG) is determined by both enthalpic (ΔH) and entropic (-TΔS) contributions: ΔG = ΔH - TΔS. While enthalpic contributions from hydrogen bonds, van der Waals interactions, and electrostatic effects are relatively intuitive to model, configurational entropy represents a particularly complex and often problematic component to quantify [51]. Configurational entropy refers to the entropy loss associated with the restriction of translational, rotational, and internal degrees of freedom when a ligand binds to its receptor [3] [9]. Despite its recognized importance, configurational entropy remains one of the most difficult thermodynamic quantities to calculate and validate against experimental measurements [51] [3].

The critical need for reliable entropy calculations stems from the phenomenon of enthalpy-entropy compensation, where improvements in binding enthalpy are frequently offset by unfavorable entropy changes [51] [9]. Without accurate entropy calculations, efforts to optimize ligand binding affinity through structure-based design may fail to achieve the desired improvements. Furthermore, different ligands binding to the same target can achieve similar affinities through completely different balances of enthalpic and entropic contributions [51]. Therefore, validating computational methods for entropy calculation against experimental binding affinity measurements represents an essential step toward reliable predictive models in drug discovery.

This technical guide examines current methodologies for calculating binding entropy, approaches for experimental validation, key challenges, and emerging directions in the field. By framing this discussion within the context of a broader thesis on the role of configurational entropy in intermolecular interactions research, we aim to provide researchers with a comprehensive resource for understanding and applying these critical concepts.

Theoretical Foundations of Binding Entropy

Components of Binding Entropy

The overall entropy change upon binding comprises several distinct contributions, each with different physical origins and computational treatments:

• Configurational Entropy: This term encompasses the loss of conformational degrees of freedom for both the ligand and protein upon binding [51]. For the ligand, this includes the restriction of internal rotatable bonds, while for the protein, it involves the reduction in sidechain and backbone flexibility at the binding interface.

• Solvation Entropy: As the binding site is desolvated during ligand binding, water molecules are released into the bulk solvent, resulting in a favorable entropy gain [51] [9]. This contribution includes both hydrophobic effects (primarily driven by entropy) and polarization entropy.

• Translational and Rotational Entropy: Upon binding, the ligand loses three translational and three rotational degrees of freedom [3]. The magnitude of this loss has been estimated to range from 4 to 11 kcal/mol in various studies [51].

The following diagram illustrates the thermodynamic cycle typically used to decompose the overall binding entropy into these constituent components:

Figure 1: Thermodynamic Cycle of Binding Entropy Components

Physical Significance in Drug Design

Understanding the balance between these entropy components has profound implications for drug design. In many cases, the net entropy change due to binding is positive, particularly for inhibitors that target systems like HIV-1 protease [9]. The hydrophobic effect, which is largely entropic in origin, often serves as a major driving force for ligand binding [51]. Additionally, the loss of ligand flexibility upon binding can be partially compensated by increased protein flexibility in certain cases, creating complex entropy redistribution patterns that are difficult to predict [3].

The concept of configurational entropy landscapes has emerged as a valuable framework for understanding these relationships. Rather than viewing entropy as a single numerical value, this perspective considers how entropy is distributed throughout the molecular system and how this distribution changes upon binding. Advanced simulation methods now allow researchers to map these landscapes and identify specific molecular regions that contribute most significantly to entropy changes [3].

Computational Methodologies for Entropy Calculation

Restraint Release (RR) Approach

The restraint release approach provides a microscopic evaluation of all relevant components to binding entropy, including configurational, polar solvation, and hydrophobic entropies [51]. In this method, strong harmonic Cartesian restraints are applied to the position of ligand atoms in both the unbound (in water) and bound (within protein active site) states. The free energy associated with releasing these restraints is then evaluated using free energy perturbation (FEP) techniques.

Key Steps in RR Methodology:

• System Preparation: Obtain starting coordinates from Protein Data Bank structures, add hydrogen atoms and water molecules using programs like MOLARIS [51].
• Charge Parameterization: Derive charge distributions for ligands from ab initio quantum calculations using packages like Gaussian03 with DFT (B3LYP/6-31G) calculations and PCM solvation model [51].
• Equilibration: Equilibrate the simulation system (protein, bound ligand, water) for 2ps at 300K with a time step of 0.5fs using molecular dynamics packages like ENZYMIX [51].
• Restraint Application: Apply harmonic restraints of the form V' = ΣiA(r⃗i − r⃗i0)² to maintain protein atoms near observed positions.
• Free Energy Calculation: Perform FEP calculations to determine the free energy change associated with releasing the restraints in both bound and unbound states.

The RR approach enables decomposition of entropy contributions that are often obscured in experimental measurements, revealing significant compensation effects between different entropy components [51].

Mutual Information Expansion (MIE)

The mutual information expansion method provides a novel and systematic approach to computing configurational entropy changes due to correlated motions from molecular simulations [3]. The second-order MIE approximation, which treats correlations between all pairs of degrees of freedom, is expressed as:

S ≈ S(2) ≡ ∑iNSi − ∑j>iNIij

Where N is the number of conformational variables (e.g., torsion angles), Si is the entropy associated with variable i, and Iij is the mutual information between coordinates i and j, defined as:

Iij ≡ Si + Sj − Sij

Where Sij is the joint entropy associated with variables i and j [3].

MIE Protocol for Protein-Ligand Binding:

• Multiple Molecular Dynamics Simulations (MMDS): Conduct microsecond-scale MD simulations of both free and bound species to ensure adequate sampling.
• Conformational Variable Selection: Identify relevant degrees of freedom (bond lengths, angles, torsions) for entropy calculation.
• Probability Distribution Calculation: Compute probability distribution functions for each variable and variable pair in both bound and unbound states.
• Mutual Information Calculation: Determine pairwise mutual information terms to account for correlated motions.
• Entropy Change Computation: Calculate the overall change in configurational entropy upon binding.

Application of MIE to the UEV domain of Tsg101 binding to an HIV-derived peptide revealed that correlations within and between the two molecules induced by binding strongly contribute to the overall loss of configurational entropy [3].

Double Decoupling Method (DDM)

The double decoupling method represents one of the most rigorous approaches for calculating absolute binding free energies and entropies [9]. This method uses alchemical free energy simulations in explicit solvent to decouple the ligand from its environment in both the binding pocket and bulk solvent.

DDM Thermodynamic Cycle:

• Ligand Desolvation: A water-solvated ligand (Lwater) is transformed into a gas phase molecule (Lgas), with free energy change -ΔG_gas→water.
• Ligand Restraint: A gas phase ligand is harmonically restrained to stay in the binding pocket (Lgas*), with free energy change ΔGgas→gas*.
• Ligand Coupling: The restrained ligand is noncovalently coupled to its environment (binding pocket and solvent), with free energy change ΔG_gas*→complex.

The absolute binding free energy is then obtained as: ΔG⁰ = ΔGgas*→complex + ΔGgas→gas* - ΔG_gas→water

To calculate binding entropy, the temperature dependence of this free energy is evaluated using: ΔS = -(∂ΔG/∂T)N,P

This requires computing binding free energies at multiple temperatures and taking the finite difference [9].

Figure 2: Double Decoupling Method Thermodynamic Cycle

Quasi-Harmonic Approximation

The quasi-harmonic approximation provides a method for estimating the free energy change due to ligand conformational restriction based on perturbation theory using the quasi-harmonic model as a reference system [53]. This approach is particularly valuable for accounting for the entropy loss when a ligand adopts a conformation in the bound state that differs from its lowest-energy conformation in solution.

Experimental Validation Approaches

Temperature-Dependent Binding Measurements

A direct approach for validating calculated entropy values involves measuring binding affinities at multiple temperatures. The binding entropy can be extracted from the temperature dependence of the binding free energy using the relationship:

ΔS = -(∂ΔG/∂T)N,P

In practice, this requires precise measurement of binding constants (Ka) at different temperatures, typically using isothermal titration calorimetry (ITC) [9]. The binding free energy is related to the binding constant by:

ΔG = -RTlnKa

Thus, by plotting ΔG versus T, the slope provides an estimate of -ΔS. This approach was used to validate entropy calculations for HIV-1 protease inhibitors Nelfinavir and Amprenavir, showing consistency between calculated and experimental trends [9].

NMR-Based Entropy Measurements

Nuclear magnetic resonance (NMR) spectroscopy provides another experimental route for validating entropy calculations. Generalized order parameters from NMR can be used to estimate changes in configurational entropy [3]. The relationship between order parameters (S²) and entropy is based on models such as the "diffusion-in-a-cone" approximation, though this approach has limitations in comprehensively capturing all entropy contributions and correlations [3].

Isothermal Titration Calorimetry (ITC)

ITC directly measures the heat changes associated with binding interactions, providing both ΔH and ΔG values. Since ΔG = ΔH - TΔS, the entropy change can be calculated from these measurements. ITC-derived entropy values serve as important benchmarks for computational methods, though it should be noted that ITC captures the total entropy change without separating configurational and solvation components [51].

Quantitative Data and Validation Results

Calculated versus Experimental Entropy Values

Table 1: Comparison of Calculated and Experimental Binding Entropies for Selected Systems

Protein-Ligand System	Calculation Method	Calculated ΔS (cal/mol·K)	Experimental ΔS (cal/mol·K)	Reference
HIV-1 PR: Nelfinavir	Double Decoupling	~30 (favorable)	Large favorable entropy	[9]
HIV-1 PR: Amprenavir	Double Decoupling	Less favorable than Nelfinavir	Less favorable than Nelfinavir	[9]
Tsg101 UEV: PTAP peptide	MIE (2nd order)	-TΔS = ~14 kcal/mol	N/A	[3]
T4 Lysozyme: Benzene	Restraint Release	Configurational + Solvation Entropies	N/A	[51]

Decomposition of Entropy Contributions

Table 2: Entropy Contribution Breakdown for Tsg101 UEV:PTAP Peptide Binding

Entropy Component	Contribution (kcal/mol)	Notes
Total First-Order Entropy Loss	14	Without correlation effects
- Tsg101 Entropy Loss	12	Dominated by reduced protein motion
- PTAP Entropy Loss	2	Ligand entropy reduction
- Torsional Entropy	12	Soft degrees of freedom most affected
- Angular Entropy	Smaller contribution	Harder degrees of freedom
- Bond Entropy	Minimal contribution	Minimal change upon binding
- Translational/Rotational	~7 (included in above)	Includes Rln8π²C⁰ term

The data from the Tsg101 UEV domain binding to the PTAP peptide illustrates several key points: protein entropy losses typically dominate over ligand entropy losses, torsional degrees of freedom contribute most significantly to entropy changes, and correlation effects can substantially influence the overall entropy change [3].

Research Reagent Solutions Toolkit

Table 3: Essential Computational Tools for Entropy Calculations

Tool/Resource	Function	Application Context
MOLARIS/ENZYMIX	Molecular dynamics package with free energy calculation capabilities	Restraint release approach; system setup and equilibration [51]
AMBER	Molecular dynamics simulation package	Double decoupling method; absolute binding free energy calculations [9] [53]
Gaussian03	Quantum chemistry package	Ligand charge parameterization for accurate force field representation [51]
Multiple Molecular Dynamics Simulations (MMDS)	Enhanced sampling approach	Mutual information expansion method; comprehensive conformational sampling [3]
ROMD (Rensselaer Online Modeling System)	QSAR modeling platform	Rank order entropy evaluation; model validation [91]
VUANT1	VUANT1, MF:C22H18N4O2S2, MW:434.5 g/mol	Chemical Reagent
ASN04885796	ASN04885796, MF:C28H28FN5O4, MW:517.6 g/mol	Chemical Reagent

Challenges and Limitations

Sampling and Convergence Issues

A fundamental challenge in entropy calculations is the adequate sampling of conformational space. Biomolecular systems often exhibit complex, multifunneled potential energy landscapes with multiple minima, making comprehensive sampling computationally demanding [92]. The convergence of entropy calculations is particularly problematic, with statistical errors in computed ΔG(bind) values estimated to be ≥2 kcal/mol in many cases [9]. Enhanced sampling methods and multiple independent simulations are often required to address these challenges [3] [92].

Force Field Inaccuracies

The accuracy of entropy calculations is inherently limited by the quality of the force fields used in simulations. Force fields are typically optimized for stable, structured proteins and may perform less reliably for flexible systems or intrinsically disordered proteins [92]. Small inaccuracies in force field parameters can lead to significant errors in entropy estimates, particularly for systems where the balance between different energy terms is delicate.

Correlation and Anharmonicity

Traditional entropy calculation methods often struggle to properly account for correlated motions and anharmonic effects. The quasiharmonic approximation becomes unreliable for molecules that sample multiple energy wells [3]. Similarly, methods based on NMR order parameters may miss important correlation effects between different bond vectors [3]. The mutual information expansion approach represents an important advance in addressing these limitations by systematically accounting for pairwise correlations [3].

Emerging Methodologies and Future Directions

Maximum Entropy Reweighting

Maximum entropy methods are emerging as powerful tools for refining conformational ensembles by integrating experimental data with molecular simulations [92]. These methods optimize the weights of conformations in an ensemble to maximize agreement with experimental observables while minimizing the deviation from the original simulation distribution. The mathematical formulation involves maximizing:

S = -∑ wᵢ ln wᵢ - ∑ λⱼ(〈Oⱼ〉 - Oⱼ_exp)²

Where wᵢ are conformation weights, λⱼ are Lagrange multipliers, 〈Oⱼ〉 are calculated observables, and Oⱼ_exp are experimental values [92].

Future methodologies are increasingly focusing on integrating diverse experimental data sources to constrain and validate entropy calculations. Techniques such as NMR chemical shifts, residual dipolar couplings, paramagnetic relaxation enhancement, and small-angle X-ray scattering provide complementary information about conformational ensembles [93] [92]. The challenge lies in developing robust computational frameworks that can simultaneously satisfy multiple experimental constraints while maintaining physical realism.

Machine Learning Approaches

Machine learning methods are beginning to be applied to entropy prediction and validation. Rank order entropy (ROE) evaluation, which assesses the stability of quantitative structure-activity relationship models in response to training set modifications, provides a framework for evaluating prediction reliability [91]. As more simulation and experimental data become available, data-driven approaches may offer complementary insights into entropy-activity relationships.

Validating entropy calculations against binding affinity measurements remains a challenging but essential endeavor in computational biophysics and drug design. The methods discussed—restraint release, mutual information expansion, double decoupling, and quasi-harmonic approximation—each offer distinct advantages and limitations. Experimental validation through temperature-dependent studies, NMR, and calorimetry provides critical benchmarks for assessing computational accuracy.

The field is moving toward more integrated approaches that combine multiple computational methods with diverse experimental data sources. Maximum entropy reweighting and other ensemble refinement techniques represent promising directions for improving the accuracy and reliability of entropy calculations. As these methodologies continue to mature, they will enhance our fundamental understanding of biomolecular recognition and improve our ability to design therapeutics with optimized binding properties.

For researchers in this field, the key recommendations are: (1) employ multiple computational methods to cross-validate results, (2) prioritize adequate sampling through enhanced simulation techniques, (3) integrate diverse experimental data for validation, and (4) carefully consider the balance between different entropy components in interpreting calculations. By addressing these priorities, the scientific community can advance toward more reliable prediction of biomolecular binding thermodynamics.

Conclusion

The pivotal role of configurational entropy in intermolecular interactions is undeniable, serving as a fundamental driver that works in concert with enthalpy to determine binding affinity and specificity. The key takeaway from integrating foundational principles, methodological advances, and practical case studies is that the most successful molecular designs—from picomolar-potency drugs to advanced materials—achieve a favorable thermodynamic balance. Moving forward, the explicit incorporation of configurational entropy into structure-activity relationships (SAR) is imperative. Future directions should focus on refining high-throughput computational methods to accurately predict entropy contributions, further elucidating the role of water networks and coupled motions, and applying these principles to emerging fields like biologics and targeted protein degradation. Embracing these thermodynamic guidelines will significantly accelerate the rational design of more effective and selective therapeutic agents and functional materials.

References

• 1. Configurational Entropy Components and Their Contribution ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9251725/]
• 2. Configuration entropy [https://en.wikipedia.org/wiki/Configuration_entropy]
• 3. Configurational Entropy in Protein-Peptide Binding ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2758778/]
• 4. The Role of Configurational Entropy in Amorphous Systems [https://pmc.ncbi.nlm.nih.gov/articles/PMC3986718/]
• 5. Computational insights on dynamic disorder in molecular ... [https://pubs.rsc.org/en/content/articlehtml/2025/ce/d5ce00209e]
• 6. Insights into Protein–Ligand Interactions: Mechanisms ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4783878/]
• 7. 13.7: The Gibbs Free Energy [https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Principles_of_Modern_Chemistry_(Oxtoby_et_al.)/Unit_4%3A_Equilibrium_in_Chemical_Reactions/13%3A_Spontaneous_Processes_and_Thermodynamic_Equilibrium/13.7%3A_The_Gibbs_Free_Energy]
• 8. Application of Hydration Thermodynamics to the Evaluation ... [https://www.mdpi.com/1099-4300/14/8/1443]
• 9. Calculations of Absolute Binding Free Energy and Entropy [https://pmc.ncbi.nlm.nih.gov/articles/PMC4127432/]
• 10. Configurational Entropy in Molecular Dynamics Simulations [https://www.nature.com/research-intelligence/nri-topic-summaries/configurational-entropy-in-molecular-dynamics-simulations-micro-2152691]
• 11. An Effective MM/GBSA Protocol for Absolute Binding Free ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8074138/]
• 12. The Role of Configurational Entropy in Amorphous Systems [https://www.mdpi.com/1999-4923/2/2/224]
• 13. Liquid anomalies and Fragility of Supercooled Antimony [https://arxiv.org/html/2510.25920v1]
• 14. Correlating thermodynamic and kinetic parameters with ... [https://www.sciencedirect.com/science/article/abs/pii/S0928098709001262]
• 15. Physical Stability of Amorphous Pharmaceuticals ... [https://www.sciencedirect.com/science/article/abs/pii/S0022354916310589]
• 16. Advancing amorphous solid dispersions through empirical ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12362086/]
• 17. Best Practices for Foundations in Molecular Simulations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6884151/]
• 18. Making Peace with Molecular Entropy [https://www.blopig.com/blog/2024/11/making-peace-with-molecular-entropy/]
• 19. Achieving accurate entropy and melting point by ab initio ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732225018288]
• 20. Trajectory Analysis — AMS 2025.1 documentation - SCM [https://www.scm.com/doc/AMS/Utilities/TrajectoryAnalysis.html]
• 21. FastMDAnalysis: Software for Automated Analysis of ... [https://chemrxiv.org/engage/chemrxiv/article-details/69097c5aef936fb4a23023b0]
• 22. Molecular Dynamics Simulation Study of the Interaction ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8391770/]
• 23. Rowan | ML-Powered Molecular Design and Simulation [https://www.rowansci.com/]
• 24. Systematic studies on the dynamics, intermolecular ... [https://www.sciencedirect.com/science/article/pii/S0167732221018225]
• 25. Intermolecular interactions probed by rotational dynamics ... [https://www.nature.com/articles/s41467-024-48822-z]
• 26. Correlation as a Determinant of Configurational Entropy in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4067153/]
• 27. Mutual information [https://en.wikipedia.org/wiki/Mutual_information]
• 28. and long-range intermolecular interactions in novel ... [https://pubmed.ncbi.nlm.nih.gov/40879496/]
• 29. Random k conditional nearest neighbor for high ... [https://peerj.com/articles/cs-2497/]
• 30. Comparative performance analysis of K-nearest neighbour ... [https://www.nature.com/articles/s41598-022-10358-x]
• 31. Enhancing K-nearest neighbor algorithm - Journal of Big Data [https://journalofbigdata.springeropen.com/articles/10.1186/s40537-024-00973-y]
• 32. Boosting K-nearest neighbor regression performance for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12482645/]
• 33. Efficient Calculation of Configurational Entropy from ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2620139/]
• 34. Telescope indexing for k-nearest neighbor search ... [https://www.nature.com/articles/s41598-025-09856-5]
• 35. Visualizing High Entropy Alloy Spaces: Methods and Best ... [https://arxiv.org/html/2408.07681v1]
• 36. Configurational entropy of protein: A combined approach ... [https://www.sciencedirect.com/science/article/abs/pii/S0009261411001473]
• 37. Isothermal Titration Calorimetry (ITC) [https://cmi.hms.harvard.edu/isothermal-titration-calorimetry]
• 38. Complementary Experimental Methods to Obtain ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC9692857/]
• 39. Calorimetric Measurements of Biological Interactions and ... [https://www.mdpi.com/1099-4300/24/4/561]
• 40. Role of configurational entropy on ordering and phase ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732211003904]
• 41. Combining Experimental Data and Computational Methods for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7594097/]
• 42. Enthalpy–entropy compensation [https://en.wikipedia.org/wiki/Enthalpy%E2%80%93entropy_compensation]
• 43. Entropy—enthalpy compensation: Fact or artifact? - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC2374136/]
• 44. Entropy, enthalpy, and evolution: Adaptive trade-offs in ... [https://www.sciencedirect.com/science/article/pii/S0959440X25000983]
• 45. Adaptive trade-offs in protein binding thermodynamics [https://pubmed.ncbi.nlm.nih.gov/40532481/]
• 46. Thinking About Aqueous Solvation [http://fbdd-lit.blogspot.com/2025/03/thinking-about-aqueous-solvation.html]
• 47. Molecular interactions: Dance of Entropy and Enthalpy [https://moleculeinsight.com/molecular-interactions/]
• 48. The contribution of entropy, enthalpy, and hydrophobic ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3151579/]
• 49. Decoding molecular recognition of inhibitors targeting HDAC2 ... [https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0273265]
• 50. STACKED – Solvation Theory of Aromatic Complexes as Key ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7189365/]
• 51. A Comprehensive Examination of the Contributions to Binding ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3064472/]
• 52. Halogenated N-phenylpiperazine and 2-(piperazin-1-yl ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12632625/]
• 53. Article Accounting for Ligand Conformational Restriction in ... [https://www.sciencedirect.com/science/article/pii/S0006349509017469]
• 54. Global Changes in Local Protein Dynamics Reduce the ... [https://www.sciencedirect.com/science/article/pii/S0022283607002367]
• 55. Quantification of the hydrophobic interaction by simulations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC33406/]
• 56. Thermodynamics of Water Displacement from Binding ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12377430/]
• 57. Water Molecules In Drug Design And Molecular Dynamics [https://www.nature.com/research-intelligence/nri-topic-summaries/water-molecules-in-drug-design-and-molecular-dynamics-micro-40489]
• 58. Entropy-driven difference in interfacial water reactivity ... [https://www.nature.com/articles/s41467-025-60298-z]
• 59. Drug binding disrupts chiral water structures in the DNA first ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d4sc08372e]
• 60. St. Jude algorithm puts water to work in drug discovery [https://www.stjude.org/media-resources/news-releases/2025-medicine-science-news/stjude-algorithm-puts-water-to-work-in-drug-discovery.html]
• 61. Water in drug design: pitfalls and good practices [https://pubmed.ncbi.nlm.nih.gov/40289543/]
• 62. Hydrophobic ion pairing enables co-loading of water ... [https://www.sciencedirect.com/science/article/pii/S0168365925003682]
• 63. Do enthalpy and entropy distinguish first in class from best ... [https://pubmed.ncbi.nlm.nih.gov/18703160/]
• 64. Do Enthalpy and Entropy Distinguish First in Class From ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2581116/]
• 65. Integrative Computational Approaches for Understanding ... [https://www.mdpi.com/1999-4915/17/6/850]
• 66. Subtype-Specific HIV-1 Protease and the Role of Hinge and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12390352/]
• 67. Activity of Human Immunodeficiency Virus Type 1 Protease ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3393404/]
• 68. Computing Clinically Relevant Binding Free Energies of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3966525/]
• 69. Importance of Polar Solvation and Configurational Entropy ... [https://pubmed.ncbi.nlm.nih.gov/23614718/]
• 70. FMO-guided design of darunavir analogs as HIV-1 ... [https://www.nature.com/articles/s41598-024-53940-1]
• 71. Quantitative Prediction of Human Immunodeficiency Virus ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11281478/]
• 72. Potent HIV‑1 protease inhibitors containing oxabicyclo ... [https://www.sciencedirect.com/science/article/abs/pii/S0960894X25000186]
• 73. Prediction and molecular field view of drug resistance in ... [https://www.nature.com/articles/s41598-022-07012-x]
• 74. HIV-1 Protease Dimerization Dynamics Reveals a ... [https://www.nature.com/articles/srep18555]
• 75. Binding thermodynamics of statins to HMG-CoA reductase [https://pubmed.ncbi.nlm.nih.gov/16128575/]
• 76. Binding thermodynamics of statins to HMG-CoA reductase. [https://connect.h1.co/article/1120606]
• 77. Binding thermodynamics of statins to HMG-CoA reductase. [https://go.drugbank.com/articles/A6283]
• 78. Statins (HMG-coenzyme A reductase inhibitors) [https://www.sciencedirect.com/science/article/abs/pii/S1570023208002043]
• 79. Intermolecular chemistry in high-entropy solid polymer ... [https://pubs.rsc.org/en/content/articlehtml/2025/ta/d5ta03675e]
• 80. Frontier advances in high-entropy electrolytes for alkali ... [https://www.sciencedirect.com/science/article/abs/pii/S0378775325025613]
• 81. The rise of high-entropy battery materials [https://www.nature.com/articles/s41467-024-45309-9]
• 82. High‑Entropy Materials: A New Paradigm in the Design of ... [https://communities.springernature.com/posts/high-entropy-materials-a-new-paradigm-in-the-design-of-advanced-batteries]
• 83. A Perspective on the Origin of High‐Entropy Solid ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12272010/]
• 84. High-entropy strategies for designing advanced solid-state ... [https://pubs.rsc.org/en/content/articlehtml/2025/cc/d5cc03141a]
• 85. Entropy-Driven Modulation of Ion Clustering and Polymer ... [https://pubmed.ncbi.nlm.nih.gov/40995777/]
• 86. Puzzle-like molecular assembly of non-flammable solid ... [https://www.nature.com/articles/s41467-025-63439-6]
• 87. Phase Stability and Transitions in High-Entropy Alloys [https://pmc.ncbi.nlm.nih.gov/articles/PMC12111454/]
• 88. First principles prediction of the Al-Li phase diagram ... [https://www.sciencedirect.com/science/article/pii/S0927025622006097]
• 89. Non-Additive Entropy Formulas: Motivation and Derivations [https://www.mdpi.com/1099-4300/25/8/1203]
• 90. First-Principles Atomistic Thermodynamics and ... [https://www.frontiersin.org/journals/chemistry/articles/10.3389/fchem.2020.00757/full]
• 91. Rank Order Entropy: why one metric is not enough - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC3428235/]
• 92. a perspective on maximum entropy methods [https://pubs.rsc.org/en/content/articlehtml/2025/cp/d5cp01263e]
• 93. Integrating experimental data and dynamics [https://www.sciencedirect.com/science/article/pii/S0959440X25001733]