Resolving Levinthal's Paradox: How Molecular Dynamics and AI Are Decoding Protein Folding

Abstract

This article explores the resolution of Levinthal's paradox—the apparent contradiction between the astronomical number of possible protein conformations and their rapid, reliable folding. It details how molecular dynamics (MD) simulations, energy landscape theory, and machine learning (ML) have transformed our understanding, moving from a random search model to a guided, funneled process. For researchers and drug development professionals, we examine the methodologies of modern protein structure prediction, address the limitations and optimization of computational tools like MD and AlphaFold, and discuss the critical validation of these models against experimental data. The synthesis of these approaches is paving the way for advanced applications in drug discovery and the design of novel therapeutics.

Deconstructing Levinthal's Paradox: From a Random Search to a Guided Folding Pathway

The protein folding problem, which encompasses the dual challenges of predicting a protein's native structure from its amino acid sequence and understanding the mechanism by which it folds, represents a grand challenge in molecular biology. The process, whereby a disordered polypeptide chain spontaneously collapses into a unique, functional three-dimensional structure, is remarkably efficient, often occurring on timescales of microseconds to milliseconds. This efficiency stands in stark contrast to Levinthal's paradox, which highlights the astronomical number of possible conformations available to an unfolded chain, making a random, exhaustive search implausible within any biologically relevant timeframe. This whitepaper examines the resolution of this paradox through the lens of energy landscape theory, which posits that folding is guided by a funnel-shaped energy landscape that efficiently directs the polypeptide toward its native state. We detail the experimental and computational methodologies that have been instrumental in probing early folding events and quantifying folding stability, and we discuss the critical implications of protein dynamics and allosteric regulation for therapeutic development.

Proteins are fundamental biological polymers that must fold into a specific three-dimensional conformation to perform their vast array of cellular functions. The "thermodynamic hypothesis", pioneered by Christian Anfinsen, established that the native structure of a protein resides in the global minimum of its Gibbs free energy under physiological conditions [1]. This implies that the amino acid sequence alone encodes the information necessary to dictate the final, functional structure.

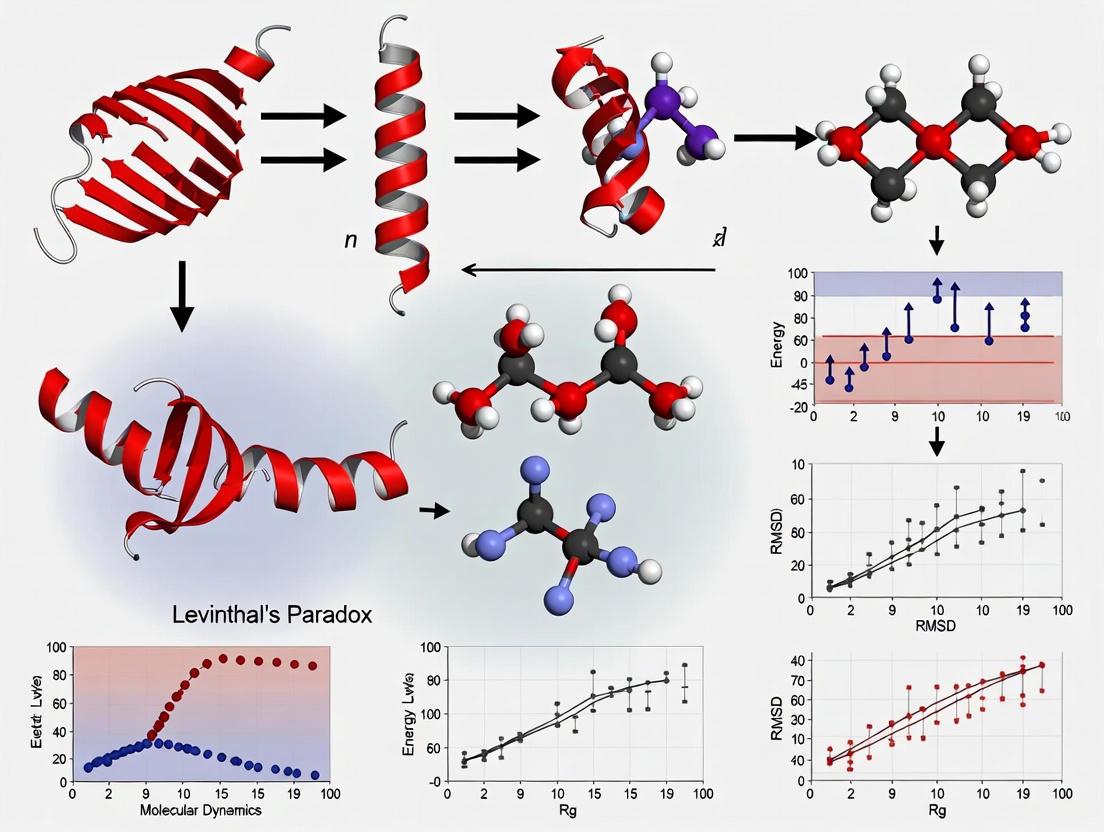
However, this thermodynamic principle initially appeared to conflict with kinetic reality. In 1969, Cyrus Levinthal noted that an unfolded polypeptide chain possesses an astronomical number of possible conformations. For a typical protein of 100 residues, if each residue can adopt even a modest number of conformations, the total conformational space can exceed 10³⁰⁰ possibilities [2]. If the protein were to randomly sample these conformations at picosecond rates, the time required to find the native state would exceed the age of the universe [3]. This is Levinthal's paradox: the stark contradiction between the vastness of conformational space and the observed rapidity of protein folding, which occurs in microseconds to seconds [2] [3].

The solution to this paradox lies in the understanding that protein folding is not a random search but a directed process. Proteins do not sample conformations indiscriminately; instead, the folding process is guided by an uneven, funnel-like energy landscape that biases the search toward the native state [2] [4]. This review will explore the theoretical frameworks, experimental methodologies, and computational advances that have collectively resolved this core paradox and deepened our understanding of protein dynamics.

Theoretical Frameworks: Resolving the Paradox

The Energy Landscape and Folding Funnel

The energy landscape theory provides a powerful conceptual framework for understanding how proteins fold rapidly. Instead of a flat landscape with a single deep minimum, the folding landscape is envisioned as a funnel [4]. At the top of the funnel, the unfolded chain has high energy and high conformational entropy. As the chain collapses into more compact, native-like structures, it loses entropy but gains stabilizing interactions, descending toward the low-energy native state at the bottom of the funnel [3].

The ruggedness of this funnel accounts for the presence of metastable intermediates and kinetic traps. A sufficiently smooth funnel allows the protein to find its native state quickly without becoming trapped in non-productive intermediates, explaining the observed fast folding times for many proteins [3].

Historical Folding Models

Several mechanistic models have been proposed to describe the protein folding pathway, each contributing to the resolution of Levinthal's paradox. The table below summarizes these key models.

Table 1: Key Theoretical Models in Protein Folding

Model	Proposed Mechanism	Contribution to Paradox Resolution
Framework / Diffusion-Collision [1] [4]	Local secondary structures (α-helices, β-sheets) form independently before assembling into tertiary structure.	Suggests folding is modular, reducing the conformational search space.
Nucleation-Condensation [1] [4]	A weak, native-like nucleus forms through a combination of local and long-range interactions, leading to cooperative folding of the entire structure.	Explains how proteins can fold in a concerted manner without fully formed secondary structures.
Hydrophobic Collapse [1]	A rapid initial collapse around hydrophobic residues forms a compact "molten globule" state, narrowing the conformational search.	Highlights the role of solvent interactions in rapidly reducing the ensemble of chains to be searched.
Foldon Model [4]	Proteins fold in a modular, hierarchical manner via independently folding units ("foldons").	Proposes a stepwise assembly process, further partitioning the folding task.

These models are not mutually exclusive; the energy landscape theory incorporates elements of each, with the dominant pathway depending on the specific protein's sequence and topology [1].

Quantitative Dimensions of the Paradox

To fully appreciate Levinthal's paradox, it is essential to consider the quantitative scales involved in protein folding. The following table contrasts the theoretical challenge with the observed biological reality.

Table 2: The Quantitative Scale of Levinthal's Paradox

Parameter	Theoretical Challenge (Random Search)	Biological Reality (Guided Search)
Conformational Space	~10³⁰⁰ possibilities for a 100-residue protein [2] [3]	Guided search of a vastly smaller subset of conformations
Time per Conformation	Picoseconds (the timescale of bond vibration) [3]	-
Theoretical Folding Time	>10¹⁰ years (longer than the age of the universe) [3]	Microseconds to minutes [3] [5]
Observed Folding Rate	-	Ranges from <1 μs to many seconds per residue [3]
Governance	-	Thermodynamic control with akinetic pathway [3]

Experimental Methodologies for Probing Folding

Understanding fast folding events requires experimental techniques with high temporal and structural resolution. The following diagram illustrates a workflow integrating several key methods discussed in this section.

Rapid Perturbation Techniques

A critical requirement for studying folding is the ability to initiate the process synchronously on a timescale faster than the events of interest.

• Rapid Mixing: Techniques like stopped-flow and continuous-flow mixing achieve rapid changes in solvent conditions (e.g., denaturant concentration) to trigger folding. Continuous-flow methods, in particular, can access the submillisecond timescale, allowing observation of very early folding events [5].
• Temperature Jump (T-Jump): This method uses a fast laser pulse to rapidly increase the temperature of the solution, perturbing the folding equilibrium. Conventional T-jump systems can access the microsecond regime [5].
• Pressure Jump (P-Jump): Advanced apparatus using piezoelectric crystals can generate pressure jumps of up to 200 bar in as little as 50 microseconds, perturbing conformational equilibria and allowing the study of relaxation kinetics [5].
• Photochemical Triggers: These approaches use light to initiate folding, for example, by photolyzing a ligand (e.g., CO from cytochrome c) that stabilizes the unfolded state, triggering refolding on a nanosecond timescale [5].

High-Throughput Stability Measurements

Recent advances have enabled the large-scale measurement of protein folding stability, providing vast datasets for understanding sequence-stability relationships.

• cDNA Display Proteolysis: This is a powerful high-throughput method that can measure the thermodynamic folding stability (ΔG) for up to 900,000 protein variants in a single experiment [6]. The method involves:
  • Creating a DNA library encoding the protein variants.
  • Using cell-free translation to generate proteins covalently linked to their cDNA.
  • Incubating the protein-cDNA complexes with a protease (e.g., trypsin or chymotrypsin).
  • Quantifying protease-resistant (folded) proteins via deep sequencing of the surviving cDNA.
  • Inferring folding stability (ΔG) using a kinetic model that accounts for cleavage rates in the folded and unfolded states [6].

This method is fast, accurate, and uniquely scalable, allowing for the comprehensive analysis of all single-point mutants in hundreds of protein domains [6].

Key Reagents and Research Tools

The following table details essential reagents and their functions in protein folding research.

Table 3: Research Reagent Solutions for Protein Folding Studies

Reagent / Tool	Function in Folding Research
Synth. DNA Oligo Pools [6]	Encodes large libraries of protein variants for high-throughput stability assays.
Cell-free cDNA Display [6]	Links a protein to its encoding cDNA, enabling in vitro selection and sequencing-based quantification.
Proteases (Trypsin/Chymotrypsin) [6]	Probes folding stability; folded proteins are resistant to cleavage.
Fluorescent Dyes/Reporters [5]	Act as sensitive probes for conformational changes during folding (e.g., FRET pairs).
Isotopically Labeled Proteins [5]	Enables detailed structural and dynamic studies using NMR spectroscopy.

Computational Approaches and Molecular Dynamics

Computational methods have been indispensable in resolving Levinthal's paradox and simulating the folding process.

• Molecular Dynamics (MD) Simulations: MD simulations model the physical movements of every atom in a protein and its solvent over time. While all-atom simulations of folding were once impossible, advances in hardware and software have made it feasible to simulate the folding of small proteins [1]. These simulations have shown that model chains can fold rapidly to their global free energy minimum, confirming thermodynamic control and demonstrating the existence of natural, rapid folding pathways [3].
• Machine Learning for Folding Rates: Machine learning algorithms are being applied to predict protein folding rates. For instance, support vector machines (SVM) and other regressors can predict logarithmic folding rates (ln(kf)) using structural parameters and network centrality measures, providing insights into the factors that determine folding speed [7].
• Elastic Network Models (ENM): These coarse-grained models represent proteins as networks of connected springs. They are highly efficient for studying large-scale collective motions and allosteric regulation, bridging the gap between static structure and dynamic function [8].

Implications for Allostery and Drug Design

The principles of protein dynamics and folding extend directly into the regulation of protein function and therapeutic intervention.

• Dynamic Allostery: Allostery is a fundamental mechanism of biological regulation where an event at one site (e.g., ligand binding) influences a distant functional site. Beyond classical models that involve major conformational changes, dynamic allostery allows for functional modulation through changes in protein dynamics and thermal fluctuations without large-scale structural shifts [9]. Evolution leverages this mechanism to fine-tune protein function through distal mutations [9].
• Therapeutic Targeting: Understanding allosteric networks and protein dynamics opens new avenues for drug discovery. Allosteric modulators can offer greater specificity than orthosteric drugs. Computational tools like MD simulations, elastic network models, and protein structure networks are critical for identifying allosteric sites and understanding how disease-associated mutations perturb allosteric communication, as seen in targets like beta-lactamases and kinases [10] [8].

Levinthal's paradox has been resolved not by discovering a single "folding pathway" but by a fundamental shift in perspective. The process is best understood as a navigation down a funneled energy landscape, where native-like interactions act as guides, making the search for the native state efficient and rapid. This understanding has been driven by the synergistic development of sophisticated experimental techniques, powerful computational simulations, and novel theoretical frameworks. The resulting insights into protein dynamics not only solve a fundamental biophysical puzzle but also provide a critical foundation for manipulating protein function in fields like biotechnology and drug design, where targeting allosteric networks and protein stability holds immense promise.

Anfinsen's Dogma and the Thermodynamic Hypothesis of the Native State

Anfinsen's Dogma, articulated by Christian B. Anfinsen in the 1960s, constitutes a foundational principle in molecular biology, positing that a protein's native three-dimensional structure is uniquely determined by its amino acid sequence under physiological conditions, representing the thermodynamically most stable state [11]. This postulate, often termed the thermodynamic hypothesis, earned Anfinsen the 1972 Nobel Prize in Chemistry and established the conceptual framework for understanding protein folding as a spontaneous self-assembly process. While this principle has guided decades of research, contemporary molecular dynamics investigations and the persistent challenge of Levinthal's paradox have revealed both the enduring validity and limitations of Anfinsen's original hypothesis. This whitepaper examines the core tenets of Anfinsen's Dogma within the context of modern protein folding research, exploring how computational approaches, particularly molecular dynamics simulations, have refined our understanding of the pathway from sequence to functional structure, and its critical implications for therapeutic development in protein misfolding diseases.

The process by which a linear polypeptide chain folds into a specific, functional three-dimensional structure represents one of the most fundamental phenomena in structural biology. Anfinsen's seminal experiments with ribonuclease A demonstrated that the protein could spontaneously refold into its native, catalytically active conformation after complete denaturation, leading to the revolutionary conclusion that all information necessary to specify the tertiary structure resides in the primary amino acid sequence [11]. This principle, termed Anfinsen's Dogma or the thermodynamic hypothesis, proposes that the native fold corresponds to the global minimum of the Gibbs free energy under physiological conditions [12].

The dogma rests upon three essential conditions that must be satisfied for a unique native structure to exist. First, the structure must be unique, meaning the amino acid sequence must not possess any alternative conformation with a comparable free energy; the global free energy minimum must be unchallenged. Second, the native state must demonstrate stability, requiring that minor perturbations to the environmental conditions do not produce substantial changes in the minimum energy configuration. This can be visualized as a free energy landscape resembling a steep funnel rather than a shallow soup plate. Third, the folded state must be kinetically accessible, implying that the pathway from the unfolded to the native state must be reasonably smooth and not involve excessively complex topological rearrangements such as knotting or other high-order conformational changes [11] [13].

The Experimental Foundation of Anfinsen's Dogma

Original Experimental Methodology

Anfinsen's foundational conclusions were derived from a series of rigorous experiments on bovine pancreatic ribonuclease A, an enzyme that catalyzes RNA hydrolysis. The key experimental protocol involved:

• Reductive Denaturation: Ribonuclease A was treated with β-mercaptoethanol to reduce its four disulfide bridges, along with 8M urea to disrupt non-covalent interactions. This treatment completely unfolded the protein and abolished its enzymatic activity [11].
• Oxidative Renaturation: The denaturing agents were subsequently removed through dialysis. Upon exposure to atmospheric oxygen, the reduced protein spontaneously reoxidized and refolded.
• Recovery Assessment: The renatured protein regained its full enzymatic activity and its original physicochemical properties, including antigenicity and protease susceptibility. Critically, the reformation of the four correct disulfide pairings occurred despite 105 possible combinations, indicating the process was not random but directed by the amino acid sequence [11] [12].

This experimental demonstration that no additional genetic information or cellular machinery was required for folding provided compelling evidence for the thermodynamic hypothesis.

Quantitative Evidence Supporting the Native State

Table 1: Key Experimental Evidence Supporting Anfinsen's Dogma

Experimental Evidence	Description	Quantitative Outcome	Interpretation
Ribonuclease A Refolding	Spontaneous refolding after reductive denaturation and reoxidation [11]	~100% recovery of enzymatic activity	Native structure is thermodynamically favored
Disulfide Bond Formation	Reformation of four specific disulfide bridges from 105 possibilities [11]	Correct pairings formed with >95% fidelity	Sequence dictates specific stabilizing interactions
In Silico Structure Prediction	Computational methods like ROSETTA achieving atomic-level accuracy for small proteins [12]	Structures predicted for 17 proteins up to 100 residues	Sequence alone sufficient to determine structure

Levinthal's Paradox and the Kinetic Accessibility Challenge

While Anfinsen's Dogma established the thermodynamic determinism of protein folding, it was Cyrus Levinthal who in 1969 highlighted the profound kinetic paradox inherent in the process. Levinthal observed that an unfolded polypeptide chain possesses an astronomical number of possible conformations. For a typical protein of 100 residues, considering just three possible conformations per residue yields approximately 3¹⁰⁰ (or ~10⁴⁸) possible structures [14].

If the protein were to randomly sample these conformations at nanosecond rates, the time required to find the native structure would exceed the age of the universe. This stands in stark contrast to the observed reality that most proteins fold on timescales of milliseconds to seconds [14]. Levinthal himself proposed the resolution to this paradox: proteins do not fold by exhaustive random search but through "speedy and guided" formation of local interactions that serve as nucleation points for subsequent folding steps—essentially, folding follows directed pathways [14].

The conceptual framework that reconciles Anfinsen's thermodynamic perspective with Levinthal's kinetic insight is the energy landscape theory. Instead of a flat landscape with countless local minima, the folding landscape is envisioned as a funnel, where the breadth represents conformational entropy and the depth represents energy. The native state resides at the bottom of this funnel, and the folding process involves a progressive narrowing of conformational space as the protein approaches its minimum energy state [4]. This funneled landscape allows proteins to fold rapidly through biased stochastic processes rather than random search.

Diagram 1: Protein Folding Energy Landscape. The funnel visualization illustrates how a protein progresses from an unfolded state (high entropy, top) to the native state (global free energy minimum, bottom). Colored pathways show successful folding via nucleation (red) and kinetic trapping in misfolded states requiring backtracking (green).

Challenges and Exceptions to Anfinsen's Dogma

While Anfinsen's Dogma provides a powerful foundational framework, contemporary research has revealed several significant exceptions and complexities that challenge its absolute validity, particularly in the complex cellular environment.

Molecular Chaperones and Cellular Folding

The discovery of molecular chaperones—proteins that assist in the folding of other proteins—appeared initially to contradict Anfinsen's sequence-sufficient premise. However, current understanding suggests that chaperones primarily prevent off-pathway interactions such as aggregation rather than providing specific structural information [11] [4]. They act as "foldases" that mitigate the challenges of folding in crowded cellular environments but do not fundamentally alter the final folded state determined by the sequence [11].

Protein Misfolding and Aggregation Diseases

A more significant challenge arises from the phenomenon of protein misfolding associated with numerous human diseases. Conditions including Alzheimer's disease, Parkinson's disease, and prion disorders like bovine spongiform encephalopathy involve proteins adopting stable, non-native conformations that evade cellular quality control mechanisms [11] [4]. Prion proteins, for instance, adopt stable conformations that differ from the native fold and can catalyze the conversion of other molecules to the same misfolded state, leading to pathogenic amyloid accumulation [11].

Non-Native Entanglement Misfolding

Recent molecular dynamics simulations have identified a specific class of misfolding involving "non-native entanglement" where proteins become kinetically trapped in off-pathway states. This occurs when:

• A gain of non-native entanglement forms: a loop structure traps another protein segment that shouldn't be threaded.
• A loss of native entanglement occurs: a necessary threading fails to form [15] [16].

These misfolded states are particularly problematic as they are often stable, soluble, and structurally similar to the native state, allowing them to evade cellular quality control systems [16]. All-atom simulations confirm that such entangled states can persist for biologically relevant timescales, especially in larger proteins where backtracking to correct the misfolding becomes energetically costly [15].

Fold-Switching Proteins

Approximately 0.5-4% of proteins in the Protein Data Bank are now recognized as "fold-switching" proteins capable of adopting multiple distinct native-like folds [11]. Examples include the KaiB protein in cyanobacteria, which switches its fold throughout the day as part of a circadian clock mechanism [11]. Such proteins exist in alternative stable states that may represent either different free energy minima or kinetically trapped conformations, with transitions driven by environmental conditions, ligand binding, or post-translational modifications.

Molecular Dynamics Simulations in Protein Folding Research

Molecular dynamics (MD) simulations have emerged as a transformative tool for investigating protein folding, enabling researchers to observe folding pathways and test hypotheses at atomic resolution and timescales previously inaccessible to experimental observation.

Simulation Methodologies

Table 2: Molecular Dynamics Approaches in Protein Folding Research

Simulation Type	Resolution Level	Key Features	Applications & Limitations
All-Atom MD	Atomic-level detail [15]	Models every atom; Newtonian equations of motion; high computational cost [12]	High-resolution folding pathways; limited to smaller proteins or shorter timescales
Coarse-Grained MD	Amino acid residue level [16]	Groups of atoms represented as single interaction sites; reduced complexity [12]	Study of larger proteins and longer timescales; loss of atomic detail
Structure-Based Models	Tertiary structural contacts [16]	Energy function biased toward native contacts; "funneled" landscape [16]	Investigation of folding mechanisms; limited for misfolding studies

Key Insights from Simulation Studies

Advanced MD simulations have provided critical insights into protein folding mechanisms:

• Folding Pathways: All-atom MD simulations have successfully tracked complete folding processes for small proteins like ubiquitin, revealing folding timescales and intermediate states that align with experimental data [16].
• Misfolding Mechanisms: As discussed previously, MD simulations have identified and characterized non-native entanglement misfolding, demonstrating how these kinetic traps form and persist [15] [16].
• Thermodynamic Validation: Free energy calculations from simulations support the thermodynamic hypothesis by showing that the native state typically corresponds to the global free energy minimum under physiological conditions [12].

The combination of simulation and experimental techniques such as hydrogen-deuterium exchange mass spectrometry (HDX-MS) and limited proteolysis has enabled the validation of predicted misfolded states and provided insights into their structural characteristics [16].

The Scientist's Toolkit: Essential Research Reagents and Methods

Table 3: Key Research Reagents and Methods for Protein Folding Studies

Reagent/Method	Function/Application	Technical Notes
Molecular Chaperones (e.g., GroEL/GroES)	Prevent aggregation and facilitate proper folding in cellular environments [4]	Essential for studying folding in vivo; not required for final structure determination
Denaturants (Urea, GdnHCl)	Unfold proteins for refolding studies; determine folding stability [11]	Used in Anfinsen's original experiments; concentration-dependent effects
Hydrogen-Deuterium Exchange Mass Spectrometry (HDX-MS)	Probes protein structure and dynamics by measuring hydrogen exchange rates [4]	Identifies structured regions and folding intermediates; used with simulation data
Molecular Dynamics Software (GROMACS, AMBER, CHARMM)	Simulates protein folding pathways and dynamics [15] [12]	All-atom and coarse-grained approaches available; requires substantial computing resources
Nuclear Magnetic Resonance (NMR) Spectroscopy	Determines protein structure and dynamics in solution [4]	Can monitor folding processes in real-time; technical complexity
Rosetta@home & AlphaFold	Predict protein structures from amino acid sequences [12]	Leverages distributed computing or neural networks; revolutionary accuracy
2-Nitropyridin-4-ol	2-Nitropyridin-4-ol|CAS 101654-28-8|High Purity	Get high-purity 2-Nitropyridin-4-ol (CAS 101654-28-8) for your research. This nitropyridine derivative is a key building block in organic synthesis. For Research Use Only.
1-benzyl-3,5-dibromo-1H-1,2,4-triazole	1-benzyl-3,5-dibromo-1H-1,2,4-triazole, CAS:106724-85-0, MF:C9H7Br2N3, MW:316.98 g/mol	Chemical Reagent

Anfinsen's Dogma remains a cornerstone principle in structural biology, correctly asserting that a protein's amino acid sequence encodes the necessary information to specify its three-dimensional structure under physiological conditions. However, seven decades of research, powered by advanced molecular dynamics simulations and experimental techniques, have revealed a more nuanced reality. The folding process occurs not through random conformational search but through guided pathways across funneled energy landscapes, with kinetic traps, chaperone assistance, and even alternative native states complicating the direct sequence-to-structure paradigm.

For researchers and drug development professionals, these insights are critically important. Understanding the mechanisms of protein misfolding, particularly long-lived kinetically trapped states, opens new therapeutic avenues for diseases ranging from neurodegeneration to aging-related disorders. Molecular dynamics simulations continue to enhance our predictive capabilities, bridging the gap between sequence and structure while illuminating the complex folding journey that Anfinsen's foundational work first revealed.

Diagram 2: Cellular Protein Folding Pathway. This workflow illustrates the journey from amino acid sequence to functional native state, highlighting the role of chaperones, cellular environment, and potential off-pathway misfolding that can lead to aggregation or degradation.

The Energy Landscape and Folding Funnel Theory as a Solution

The protein folding problem represents one of the most fundamental challenges in molecular biology. In 1969, Cyrus Levinthal posed his famous paradox, highlighting the stark contradiction between the vast conformational space available to an unfolded polypeptide chain and the rapid, reproducible folding observed in biological systems [17] [4]. Levinthal noted that a random, sequential search of all possible conformations would require timescales vastly exceeding the age of the universe, yet proteins typically fold on timescales of milliseconds to seconds [18]. This paradox created a conceptual impasse that persisted for decades.

The resolution to this paradox emerged not from a pathway-centric view, but from a radical shift in perspective: the energy landscape theory and its central metaphor, the folding funnel [18]. First introduced by Ken A. Dill in the 1980s, this theory reframes protein folding not as a random search, but as a guided, energetically biased process where a protein progressively navigates towards its native state through a funnel-shaped energy landscape [18]. This review explores how the folding funnel theory provides a comprehensive solution to Levinthal's paradox, its experimental and computational validation, and its critical implications for molecular dynamics research and drug development.

Theoretical Foundations of the Folding Funnel

Core Principles of the Energy Landscape

The folding funnel hypothesis is a specific version of the energy landscape theory that visualizes the protein folding process as a progressive narrowing of conformational possibilities toward the native state. The key to resolving Levinthal's paradox lies in understanding that folding is not a random search but a directed, multi-pathway process governed by the topology of this energy landscape [18].

The landscape is characterized by two fundamental dimensions: depth, representing the energetic stabilization of the native state, and width, representing the conformational entropy of the system [18]. As the protein folds, it loses conformational entropy (moving down the funnel) while gaining favorable native contacts (decreasing in energy). The theory posits that the native state corresponds to the global free energy minimum under physiological conditions, consistent with Christian Anfinsen's thermodynamic hypothesis [18] [4].

Table 1: Key Characteristics of Protein Energy Landscapes

Characteristic	Description	Implication for Folding
Funnel Shape	Wide at the top (unfolded states), narrow at the bottom (native state)	Directs the search toward the native state
Landscape Ruggedness	Presence of hills, valleys, and local minima	Can create kinetic traps for partially folded intermediates
Thermodynamic Stability	Native state occupies the global free energy minimum	Ensures the native state is thermodynamically favored
Multi-Dimensionality	Landscape defined by many conformational coordinates	Allows for multiple parallel folding pathways

Resolving Levinthal's Paradox

The funnel landscape resolves Levinthal's paradox through several key mechanisms:

• Non-Random Search: The search is not random but is biased toward the native state by energetically favorable interactions, particularly the hydrophobic effect [18]. The sequestration of hydrophobic residues away from water provides a major driving force, in a process known as hydrophobic collapse.
• Parallel Pathways: The funnel accommodates numerous parallel folding routes, meaning different molecules of the same protein can follow microscopically different pathways to reach the same native structure [18]. This massively parallel search drastically reduces the effective folding time.
• Progressive Organization: Folding proceeds through the progressive organization of an ensemble of partially folded structures, rather than a single pathway with mandatory intermediates [18]. This is described as a "divide-and-conquer" strategy, where local structures form first, followed by global assembly [18].

Quantitative Models and Landscape Topographies

Theoretical models have proposed specific topographies for the folding funnel, each with distinct implications for folding kinetics and mechanisms.

Classical Funnel Models

Dill and Chan illustrated several landscape models that depict possible folding routes [18]:

• The "Golf-Course" Landscape: A hypothetically flat landscape where a random search would be impossible, highlighting the necessity of a biased, funneled landscape.
• The Ideal Smooth Funnel: A landscape with minimal energetic barriers, allowing rapid, direct descent to the native state.
• The Rugged Funnel: Contains many local minima and barriers, representing kinetic traps where partially folded structures can become transiently stuck.
• The "Moat" Landscape: Features an obligatory kinetic trap that a significant population of molecules must navigate through.
• The "Champagne Glass" Landscape: Characterized by a significant free energy barrier, often related to conformational entropy, that must be overcome before rapid folding can proceed.

The Foldon Volcano Model

A significant variation, the Foldon Funnel Model proposed by Rollins and Dill, suggests the energy landscape has a volcano shape rather than a simple funnel [18]. In this model, the initial formation of native-like secondary structures is energetically unfavorable (uphill in free energy) and is only stabilized by subsequent tertiary interactions. The highest free energy point is the step just before reaching the native state, consistent with experimental observations that isolated secondary structures are often unstable [18].

Experimental Validation and Probes

The predictions of the energy landscape theory have been tested and supported by a range of sophisticated experimental techniques.

Single-Molecule Force Spectroscopy

Single-molecule techniques, particularly magnetic tweezers, have emerged as powerful tools for directly probing protein folding dynamics under force. In magnetic tweezers, a single protein is tethered between a glass surface and a magnetic bead. Application of a magnetic field exerts a piconewton-scale force to stretch the protein, while its extension is tracked with nanometer precision [19]. This method provides intrinsic force-clamp conditions and exceptional stability, enabling long-term measurement of equilibrium folding and unfolding transitions for individual molecules, free from ensemble averaging [19]. Other key techniques include atomic force microscopy (AFM) and optical tweezers.

Hydrogen-Deuterium Exchange (HDX)

HDX coupled with mass spectrometry or NMR can probe the structure and dynamics of folding intermediates by measuring the rate at which backbone amide hydrogens exchange with deuterium from the solvent. This technique provided key evidence for the foldon model, revealing that proteins can fold in a modular, hierarchical manner with discrete units (foldons) attaining native-like structure at different stages [4].

Table 2: Key Experimental Methods for Probing Energy Landscapes

Method	Key Measurable	Application to Landscape Theory
Single-Molecule Magnetic Tweezers	End-to-end extension changes under constant force; folding/unfolding rates	Directly measures dynamics and stability under mechanical perturbation; maps free energy landscapes [19]
Hydrogen-Deuterium Exchange (HDX)	Solvent accessibility of backbone amides; protection factors	Identifies structured regions in intermediates; validates hierarchical folding (e.g., Foldons) [4]
Single-Molecule FRET (smFRET)	Distance between two fluorophores on a protein	Probes conformational heterogeneity and dynamics of ensembles in real-time
NMR Spectroscopy	Chemical shifts, relaxation rates	Provides atomic-resolution data on protein dynamics and transiently populated states

Diagram 1: The Folding Funnel Concept. The funnel visualizes the progressive decrease in conformational entropy and energy as a protein transitions from an unfolded state to its native structure.

Computational Approaches and Molecular Dynamics

Computer simulations, particularly molecular dynamics (MD), have been instrumental in visualizing and quantifying the folding process in atomic detail, providing a critical link between theory and experiment.

All-Atom Molecular Dynamics Simulations

All-atom MD simulations explicitly model every atom in a protein and its solvent environment, integrating Newton's equations of motion to trace atomic trajectories [20]. The careful preparation of the initial system—including solvation, energy minimization, and thermalization—is vital to avoid fictitious behavior and ensure biological relevance [20]. While tremendously powerful, a significant limitation is the timescale barrier; folding events often occur on timescales (milliseconds to seconds) that are computationally prohibitive to simulate with standard MD.

Enhanced Sampling and Free Energy Methods

To overcome timescale limitations, advanced computational techniques have been developed:

• Essential Dynamics Sampling (EDS): This technique biases a simulation to explore configurations along collective motions derived from an analysis of the protein's natural dynamics, allowing efficient sampling of the folding pathway [21].
• Free Energy Perturbation (FEP): FEP is a physics-based method used to calculate the free energy differences between two states, such as a wild-type protein and a mutant. Modern protocols like QresFEP-2 use a hybrid-topology approach to efficiently and accurately predict the effects of point mutations on protein stability, which is crucial for drug design and understanding disease [22].

Diagram 2: MD Simulation Workflow. A generic protocol for all-atom molecular dynamics simulations of protein folding/unfolding in solution.

Table 3: Essential Research Reagents and Tools for Protein Folding Studies

Reagent / Tool	Function / Application	Example / Note
Molecular Dynamics Software	All-atom simulation of folding pathways and dynamics	GROMACS [22], ENCAD [20], AMBER, CHARMM
Free Energy Perturbation (FEP) Protocols	Predict mutational effects on stability & binding	QresFEP-2 (hybrid-topology) [22], FEP+ (dual-topology)
Superparamagnetic Beads	Force probe for magnetic tweezers experiments	~1-5 µm beads, tethered via engineered cysteines [19]
Fluorescent Dyes	Labeling for smFRET and fluorescence spectroscopy	Cy3/Cy5, Alexa Fluor dyes for distance measurements
Site-Directed Mutagenesis Kits	Engineer protein variants to test stability	Alanine scanning, Foldon disruption, disease mutation models
AI-Based Structure Prediction	Generate structural hypotheses and models	AlphaFold2, SimpleFold (general-purpose transformer) [23]

Implications for Drug Discovery and Human Health

The energy landscape perspective has profound implications beyond basic science, particularly in understanding disease and guiding therapeutic development.

Many human diseases, including neurodegenerative disorders like Alzheimer's and Parkinson's, are linked to protein misfolding and aggregation [4]. A rugged energy landscape with deep kinetic traps can favor the population of misfolded states that self-assemble into toxic aggregates. The cellular proteostasis network—a system of chaperones, folding enzymes, and degradation machinery—functions to maintain a smooth, functional landscape [4]. Age-related decline in proteostasis capacity can lead to a failure to manage this landscape, resulting in disease.

In drug discovery, the concept of conformational selection derived from landscape theory is fundamental. Rather than inducing a single conformational change, drugs often bind to and stabilize pre-existing, low-population conformations within the native-state ensemble, shifting the equilibrium [24]. This shifts the energy landscape itself, stabilizing active or inactive states, which is a key mechanism for allosteric drugs and for designing inhibitors that target specific conformational states.

The energy landscape and folding funnel theory has successfully provided a unified framework to resolve Levinthal's paradox. It demonstrates that proteins fold rapidly not by examining all possible conformations, but by navigating a funneled energy landscape that biases the search toward the native state through a combination of energetically favorable interactions and ensemble-based parallel pathways.

Future research will focus on exploring the most rugged parts of the landscape, understanding the folding of large multi-domain proteins and complexes, and further integrating computational predictions with experimental validation. The continued development of advanced MD protocols like QresFEP-2 [22] and novel AI-based structure prediction tools like SimpleFold [23] will further bridge the gap between predicting structure and understanding the dynamical folding process. The application of these principles will continue to illuminate the mechanisms of biological function and disease, and accelerate the rational design of therapeutics.

The protein folding problem has been predominantly studied in simplified, optimized in vitro conditions, yielding fundamental physicochemical principles of folding landscapes. However, a significant gap persists between this foundational knowledge and the complex reality of folding within the living cell. This whitepaper delineates the critical distinctions between in vitro and in vivo protein folding environments, emphasizing the role of macromolecular crowding, vectorial synthesis, chaperone assistance, and evolutionary pressures. By framing these differences within the context of Levinthal's paradox and advances in molecular dynamics research, we provide a technical guide for researchers and drug development professionals to bridge the conceptual and experimental divides, fostering a more predictive understanding of protein behavior in biological and therapeutic contexts.

The classic in vitro experiments of Christian Anfinsen demonstrated that a protein's amino acid sequence contains all the information necessary to specify its three-dimensional native structure [25]. This principle has guided decades of research, yielding profound insights into protein folding kinetics and thermodynamics under controlled, dilute buffer conditions. However, the cellular environment presents a fundamentally different set of challenges and influences that distinguish the in vivo folding process from its in vitro counterpart.

Levinthal's paradox highlights the core theoretical problem: a random, brute-force search of all possible conformations would take an astronomical amount of time, far longer than the age of the universe, for a protein to find its native state [14]. Yet, proteins fold spontaneously on millisecond to second timescales. The resolution to this paradox lies in the concept of funneled energy landscapes, where proteins do not sample conformations randomly but are guided toward the native state by biased interactions [14]. While this theory explains rapid folding in vitro, the in vivo environment introduces additional layers of complexity that further reshape this energy landscape. The cell is not a dilute aqueous solution; it is an extremely crowded, organized, and active environment where folding occurs concurrently with synthesis, alongside myriad interactions that can either facilitate or hinder the journey to the functional native structure.

Fundamental Environmental Differences: A Comparative Analysis

The environment in which a protein folds profoundly influences its pathway, kinetics, and success rate. The following table summarizes the key differentiating factors between the test tube and the cellular milieu.

Table 1: Key Differences Between In Vitro and In Vivo Folding Environments

Factor	In Vitro Folding	In Vivo Folding
Initiation	Refolding of full-length, denatured polypeptide chains [26]	Co-translational folding during ribosomal synthesis; vectorial folding during secretion [26] [25]
Macromolecular Crowding	Absent or minimal (highly dilute solutions) [26]	Extremely high (200–400 mg/mL total macromolecule concentration) [26]
Chaperone Assistance	Typically absent unless specifically added	Essential for a significant fraction of proteins; prevents aggregation and aids folding [26]
Spatial Organization	Homogeneous solution	Highly organized; compartmentalized (e.g., cytosol, endoplasmic reticulum, organelles) [26]
Unfolded State Population	Sampled freely in dynamic equilibrium governed by thermodynamic stability [26]	Disfavored due to chaperone binding, ongoing degradation, and kinetic barriers [26]
Competition with Aggregation	Governed by simple second-order kinetics; high concentration leads to aggregation [27]	Kinetic competition between folding, aggregation, and chaperone intervention; aggregation is a dangerous side reaction [26] [27]
Energy Landscape	Governed primarily by intrinsic protein sequence and solvent conditions	Reshaped by crowding, weak "quinary" interactions, and helper proteins [26]

The Impact of the Cellular Milieu

The crowded cellular environment, with macromolecule concentrations ranging from 200 to 400 mg/ml, was initially thought to influence folding primarily through excluded volume effects, which favor more compact folded states. However, recent work suggests that the influence may be dominated by a high density of weak, transient, non-specific interactions, sometimes termed "quinary" interactions [26]. These interactions can either stabilize or destabilize native proteins and their intermediates, effectively reshaping the folding energy landscape in a manner difficult to replicate in the test tube.

Vectorial Folding: The Role of Synthesis and Secretion

A fundamental distinction is the vectorial nature of folding in vivo. In vitro refolding typically begins from an ensemble of full-length, denatured chains. In the cell, proteins are synthesized by the ribosome from the N to the C terminus, allowing the nascent chain to begin folding before synthesis is complete [26] [25]. This co-translational folding can prevent non-productive interactions that might occur if the entire chain were present simultaneously and can populate productive folding intermediates [25].

A striking example of vectorial folding is found in autotransporter proteins from Gram-negative bacteria. These virulence factors are secreted across the outer membrane from the C to the N terminus. This directional secretion, coupled with an anisotropic distribution of folding stability along the polypeptide chain, promotes rapid folding on the cell surface and may even provide a driving force for efficient secretion [25]. This stands in stark contrast to the refolding of a full-length autotransporter protein in vitro, which proceeds orders of magnitude more slowly [25].

Table 2: Experimental Techniques for Studying Folding Across Environments

Technique	Application	Key Insights Provided
Single-Molecule FRET	In vitro & in vivo (via microscopy)	Measures intra-molecular distances, folding pathways, and metastable states in real-time [26]
Optical Tweezers	Primarily in vitro	Applies mechanical force to unfold/refold proteins, revealing transition paths and intermediate states [26]
Fluorescence Relaxation Imaging (FReI)	In vivo	Monitors protein folding and stability inside living cells using FRET and temperature or denaturant jumps [28]
NMR Spectroscopy	In vitro & in vivo	Provides atomic-resolution data on protein structure, dynamics, and populations of conformational states
Machine-Learned Coarse-Grained (CG) MD	In silico	Predicts folding pathways, metastable states, and effects of mutations at a fraction of the computational cost of all-atom MD [29]

Resolving Levinthal's Paradox: From Theory to Cellular Reality

Levinthal's paradox posits that a random conformational search for the native state would take an impossibly long time, implying the existence of guided folding pathways [30] [14]. In vitro studies resolved this by introducing the concept of a funneled energy landscape, where native-like interactions are preferentially stabilized, leading the protein efficiently to its native state [14].

The in vivo environment introduces additional factors that further resolve this paradox. Co-translational folding reduces the conformational search space dramatically. By starting from a much smaller ensemble of conformations and building the protein incrementally, the cell avoids the Levinthal search problem for the entire chain at once [25]. Furthermore, molecular chaperones do not typically provide steric information for folding but instead suppress off-pathway reactions like aggregation, effectively smoothing the energy landscape and allowing the protein's intrinsic sequence-based preferences to guide it to the native state more reliably [26]. The crowded milieu, through a combination of excluded volume and quinary interactions, can also bias the landscape toward more compact, native-like states.

The following diagram illustrates how the cellular environment shapes the protein folding energy landscape compared to the in vitro scenario.

Advanced Computational and Experimental Methodologies

The Rise of Machine-Learned Molecular Dynamics

Molecular dynamics (MD) simulation is a powerful tool for elucidating folding pathways. All-atom MD provides high resolution but at an extreme computational cost, limiting its application to small proteins and short timescales [29]. Recent breakthroughs involve the development of machine-learned coarse-grained (CG) models. These models are trained on diverse all-atom simulation datasets and can then be used for extrapolative MD on new protein sequences.

One such model, CGSchNet, demonstrates transferability across sequence space, successfully predicting metastable states of folded, unfolded, and intermediate structures for proteins not included in its training set [29]. This approach is several orders of magnitude faster than all-atom MD, making it feasible to simulate the folding of larger proteins like the 73-residue alpha3D and to compute relative folding free energies of mutants [29]. This represents a significant step toward a universal, predictive simulation tool that can bridge the gap between in vitro and in vivo folding by potentially incorporating cellular factors.

Quantitative Kinetic Models for In Vivo Folding

Understanding folding in the cell requires quantitative models that account for kinetic competition. A foundational model describes the competition between first-order folding and second-order aggregation during de novo protein synthesis [27]. The yield of native protein in vivo depends not only on the rates of folding and aggregation but also on the rate of protein synthesis itself. This framework explains why the cell has evolved mechanisms, such as molecular chaperones, to influence these rates and prevent unproductive aggregation [27].

The following diagram outlines a generalized experimental workflow for integrating in vitro and in vivo data to build predictive models of cellular folding, a approach relevant to both protein and RNA folding [31].

The Scientist's Toolkit: Essential Research Reagents and Solutions

Table 3: Key Reagent Solutions for Protein Folding Research

Research Reagent / Tool	Function in Folding Studies
Chemical Denaturants (e.g., Urea, GdnHCl)	Unfold proteins in vitro to initiate refolding studies; used to measure protein stability [25].
Fluorescent Dyes (for FRET)	Label proteins to act as donor/acceptor pairs in Förster Resonance Energy Transfer, reporting on intra-molecular distances and conformational changes [26] [28].
Molecular Chaperones (e.g., Hsp70)	Purified chaperones are used in vitro to study their mechanism of action in preventing aggregation and facilitating folding [26] [28].
Crowding Agents (e.g., Ficoll, Dextran)	Polymers used in vitro to mimic the excluded volume effects of the crowded cellular environment [26].
Machine-Learned Coarse-Grained (CG) Force Fields	Computational models that dramatically increase simulation speed while maintaining accuracy for predicting folding pathways and free energies [29].
Optical Tweezers	Instrument that uses laser light to manipulate beads attached to a protein, allowing the application of precise forces to study unfolding/refolding mechanics [26].
1-[4-(Trifluoromethyl)benzyl]piperazine	1-[4-(Trifluoromethyl)benzyl]piperazine, CAS:107890-32-4, MF:C12H15F3N2, MW:244.26 g/mol
Methyl 2-amino-1H-benzo[d]imidazole-5-carboxylate	Methyl 2-amino-1H-benzo[d]imidazole-5-carboxylate, CAS:106429-38-3, MF:C9H9N3O2, MW:191.19 g/mol

The distinction between in vitro and in vivo protein folding is not merely a technicality but a fundamental consideration for understanding biology and developing therapeutics. The cellular environment—with its crowding, spatial organization, helper proteins, and vectorial synthesis—actively participates in the folding process, reshaping energy landscapes and ensuring efficiency and fidelity. Levinthal's paradox, resolved in vitro by the concept of funneled landscapes, is further resolved in vivo by these additional biological factors that guide the search for the native state.

Future research must continue to bridge the gap between these two worlds. This will involve developing more sophisticated in vitro systems that better mimic cellular conditions, advancing in vivo measurement techniques with greater spatial and temporal resolution, and creating next-generation computational models that can integrate the multitude of factors present in the cell. As these fields converge, we move closer to a truly predictive understanding of protein folding, misfolding, and aggregation in human health and disease, ultimately enabling more rational drug design and therapeutic interventions.

Computational Arsenal: MD Simulations, AI, and Advanced Sampling for Protein Dynamics

The fundamental challenge in structural biology is understanding how a protein's one-dimensional amino acid sequence dictates its unique, functional three-dimensional structure. This process, known as protein folding, is central to all biological function and is famously encapsulated by Levinthal's paradox, which highlights the astronomical improbability of a protein randomly searching all possible conformations to find its native state [17] [4]. Despite this, proteins in nature fold reliably and rapidly, suggesting the existence of specific folding pathways guided by a funnel-shaped energy landscape [4]. Molecular Dynamics (MD) has emerged as a powerful computational technique that directly addresses this paradox by simulating the physical motions of atoms and molecules over time, effectively providing a "computational microscope" to observe biological processes at an atomic level of detail [32] [33]. The core of any MD simulation is the force field—a set of mathematical functions and parameters that describe the potential energy of a molecular system as a function of the coordinates of its atoms [34] [35]. This whitepaper explores the principles of MD simulations, the construction and function of force fields, and their indispensable role in bridging the gap between sequence, structure, and function, thereby offering a resolution to the conceptual challenges posed by Levinthal.

Molecular Dynamics: A Theoretical Framework

Basic Principles and Historical Context

Molecular Dynamics is a computer simulation method for analyzing the physical movements of atoms and molecules. The core principle involves numerically solving Newton's equations of motion for a system of interacting particles, where forces between particles and their potential energies are calculated using interatomic potentials or molecular mechanical force fields [32]. Given the positions of all atoms, the force on each atom is calculated, and Newton's laws are used to predict its new position and velocity after a very short time step, typically on the order of femtoseconds (10⁻¹⁵ s) [33]. This process is repeated millions or billions of times to generate a trajectory—a dynamic view of the system's evolution over time [33].

The method has its roots in the late 1950s with simulations of simple gasses [32]. The first MD simulation of a protein was performed in the late 1970s, and the foundational work enabling these simulations was recognized by the 2013 Nobel Prize in Chemistry [33]. Initially a tool for theoretical physicists and materials scientists, MD has since become a cornerstone technique in biochemistry and biophysics, propelled by exponential growth in computational power and algorithmic improvements [32].

Addressing Levinthal's Paradox with MD

Levinthal's paradox points out the impossibility of a protein finding its native state via a random conformational search, as the number of possible conformations is astronomically large [17] [36]. MD simulations offer a solution to this paradox not by performing this random search, but by simulating the actual physical forces that guide the protein along a biased, energetically favorable pathway.

The energy landscape theory of protein folding, which frames folding as a funnel-guided process where native states occupy energy minima, is perfectly suited for investigation via MD [4]. Simulations can directly probe this landscape, revealing the kinetic pathways and intermediate states that proteins traverse as they fold. Furthermore, MD can capture the crucial role of the cellular environment, including solvent effects and molecular chaperones, which help proteins avoid misfolding and aggregation, thus explaining how reliable folding occurs in vivo despite the paradox [4]. While pure ab initio folding of proteins from an unfolded state remains computationally demanding, MD simulations are increasingly used to refine predicted structures and study conformational dynamics critical to biological function [32] [37].

The Engine of Simulation: Molecular Mechanics Force Fields

The Concept of a Force Field

A force field is a computational model used to calculate the potential energy of a system of atoms based on their positions [34]. It consists of two key components:

• The functional form, which is the mathematical expression for the different energy terms.
• The parameter sets, which are the specific numerical values (e.g., equilibrium bond lengths, force constants, atomic charges) used in the functions for different types of atoms and bonds [34] [38].

The basic functional form decomposes the total potential energy ((E{total})) into contributions from bonded interactions (atoms linked by covalent bonds) and non-bonded interactions (atoms in different molecules or separated by three or more bonds) [34] [35]: (E{total} = E{bonded} + E{non-bonded})

Components of a Biomolecular Force Field

The energy terms in a typical Class I biomolecular force field (e.g., AMBER, CHARMM, OPLS) are detailed below.

Bonded Interactions

Bonded interactions describe the energy associated with the covalent geometry of the molecule.

• Bond Stretching: The energy required to stretch or compress a covalent bond from its equilibrium length. It is typically modeled by a harmonic potential: (E{bond} = \sum{bonds} \frac{kb}{2}(l{ij} - l0)^2) where (kb) is the bond force constant, (l{ij}) is the actual bond length, and (l0) is the equilibrium bond length [34] [35].

• Angle Bending: The energy required to bend the angle between three bonded atoms from its equilibrium value. Also modeled by a harmonic potential: (E{angle} = \sum{angles} \frac{k\theta}{2}(\theta{ijk} - \theta0)^2) where (k\theta) is the angle force constant, (\theta{ijk}) is the actual angle, and (\theta0) is the equilibrium angle [34] [35].

• Torsion (Dihedral) Angle Rotation: The energy associated with rotation around a central bond connecting four sequentially bonded atoms. This term describes the periodicity of energy barriers and is modeled by a periodic function: (E{dihedral} = \sum{dihedrals} k\phi[1 + cos(n\phi - \delta)]) where (k\phi) is the dihedral force constant, (n) is the periodicity (number of minima in 360°), (\phi) is the dihedral angle, and (\delta) is the phase shift [34] [35].

• Improper Torsions: Used primarily to enforce planarity in aromatic rings and other conjugated systems, often using a harmonic potential [35].

Non-Bonded Interactions

Non-bonded interactions describe the forces between atoms that are not directly covalently bonded.

• Van der Waals Forces: These include short-range attractive (dispersion) and repulsive (Pauli exclusion) forces. They are most commonly described by the Lennard-Jones 12-6 potential: (E{vdW} = \sum{i{ij} \left[ \left(\frac{\sigma{ij}}{r{ij}}\right)^{12} - \left(\frac{\sigma{ij}}{r{ij}}\right)^{6} \right]) where (\epsilon{ij}) is the depth of the potential well, (\sigma{ij}) is the distance at which the interparticle potential is zero, and (r{ij}) is the distance between atoms [34] [35]. The (r^{-12}) term describes repulsion, while the (r^{-6}) term describes attraction.}>

• Electrostatic Interactions: The classical interaction between partial atomic charges, calculated using Coulomb's law: (E{elec} = \sum{ii qj}{4\pi\epsilon0 \epsilonr r{ij}}) where (qi) and (qj) are the partial charges on atoms, (r{ij}) is their distance, (\epsilon0) is the permittivity of free space, and (\epsilonr) is the relative dielectric constant [34] [35].}>

Table 1: Core Energy Terms in a Classical Biomolecular Force Field

Interaction Type	Mathematical Form	Key Parameters	Physical Description
Bond Stretching	(E = \frac{kb}{2}(l - l0)^2)	(kb) (force constant), (l0) (eq. length)	Energetic cost of stretching/compressing a covalent bond.
Angle Bending	(E = \frac{k\theta}{2}(\theta - \theta0)^2)	(k\theta) (force constant), (\theta0) (eq. angle)	Energetic cost of bending the angle between three bonded atoms.
Torsion (Dihedral)	(E = k_\phi[1 + cos(n\phi - \delta)])	(k_\phi) (barrier height), (n) (periodicity), (\delta) (phase)	Energy barrier for rotation around a central bond; defines conformational preferences.
Van der Waals	(E = 4\epsilon \left[ (\frac{\sigma}{r})^{12} - (\frac{\sigma}{r})^{6} \right])	(\epsilon) (well depth), (\sigma) (vdW radius)	Short-range attraction and repulsion between electron clouds.
Electrostatic	(E = \frac{qi qj}{4\pi\epsilon_0 r})	(qi, qj) (atomic partial charges)	Long-range attraction/repulsion between charged or polar atoms.

The following diagram illustrates the relationships between these different energy components and the overall potential energy calculation in a force field.

Parameterization and Classification of Force Fields

The accuracy of a force field is entirely dependent on the quality of its parameters. These are derived from a combination of quantum mechanical calculations on small molecules and experimental data, such as enthalpies of vaporization, liquid densities, and spectroscopic properties [34]. A critical concept in force field development is the definition of atom types, which classify atoms not only by their element but also by their chemical environment (e.g., an oxygen in a carbonyl group vs. an oxygen in a hydroxyl group) [34] [38].

Force fields can be broadly categorized into several classes:

• Class I (e.g., AMBER, CHARMM, OPLS): Use simple harmonic potentials for bonds and angles and do not include explicit cross-terms. They offer a good balance of accuracy and computational efficiency for biomolecular simulations [35] [38].
• Class II (e.g., MMFF94): Include anharmonic terms and cross-terms coupling bonds, angles, and dihedrals for higher accuracy in small molecules [35].
• Class III (Polarizable Force Fields, e.g., AMOEBA, Drude): Explicitly model the redistribution of electron density (polarization) in response to the environment, using methods like inducible point dipoles or Drude oscillators. These are more accurate but computationally expensive [35].

Table 2: Popular Biomolecular Force Fields and Their Characteristics

Force Field	Class	Common Applications	Key Features
AMBER	I	Proteins, Nucleic Acids	Well-parameterized for standard biomolecules; widely used in drug discovery.
CHARMM	I	Proteins, Lipids, Carbohydrates	Broad coverage of biomolecules and membrane systems.
OPLS	I	Proteins, Organic Molecules	Optimized for liquid-state properties and protein-ligand interactions.
GROMOS	I	Biomolecules in solution	Unified atom approach (hydrogens combined with heavy atoms); parameterized for consistency with experimental data.
AMOEBA	III	Polarizable Systems	Includes induced atomic dipoles; improved description of electrostatic interactions.

Practical Implementation and Protocol

Setting up and running an MD simulation involves a standardized workflow. The diagram below outlines the key steps, from initial structure preparation to final trajectory analysis.

Step 1: Initial Structure Preparation The simulation begins with an initial atomic coordinate set, typically obtained from the Protein Data Bank (PDB), from AI-based prediction tools like AlphaFold, or from de novo modeling [36]. This structure must be checked for missing atoms, protonation states, and disulfide bonds.

Step 2: System Setup The biomolecule is placed in a simulation box, which is then filled with solvent molecules (e.g., TIP3P, SPC/E water models). Ions are added to neutralize the system's charge and to achieve a physiologically relevant salt concentration [32] [33]. The choice between an explicit solvent model (more accurate but costly) and an implicit solvent model (mean-field approximation, faster) is a key consideration [32].

Step 3: Energy Minimization The system is energy-minimized to remove any steric clashes or unphysical geometry introduced during setup. This step finds the nearest local energy minimum by algorithms like steepest descent or conjugate gradient [32].

Step 4: Equilibration Before production data collection, the system must be equilibrated under the desired thermodynamic conditions.

• NVT Equilibration: The Number of particles, Volume, and Temperature are held constant. This allows the system to reach the target temperature (e.g., 310 K).
• NPT Equilibration: The Number of particles, Pressure, and Temperature are held constant. This allows the density of the system (e.g., solvent box) to adjust to the target pressure (e.g., 1 bar) [32].

Step 5: Production MD This is the main simulation phase where the trajectory used for analysis is generated. The system is propagated for nanoseconds to microseconds, with coordinates and velocities saved at regular intervals [32] [33]. The long timescales required to observe many biologically relevant processes (e.g., protein folding) remain a key computational challenge.

Step 6: Trajectory Analysis The saved trajectory is analyzed to extract biologically meaningful information. Common analyses include:

• Calculating Root Mean Square Deviation (RMSD) to measure structural stability.
• Determining Root Mean Square Fluctuation (RMSF) to identify flexible regions.
• Studying hydrogen bonding networks and salt bridge formation.
• Performing principal component analysis (PCA) to identify large-scale collective motions [33].

Table 3: Essential "Research Reagent Solutions" for an MD Simulation

Item / Resource	Category	Function / Purpose
Protein Data Bank (PDB)	Input Structure	Repository of experimentally determined 3D structures of proteins and nucleic acids to use as starting points.
AlphaFold Protein Structure Database	Input Structure	Source of highly accurate predicted protein structures for proteins with unknown experimental structures [36].
AMBER/CHARMM/OPLS Force Field	Energy Model	Defines the mathematical functions and parameters for calculating potential energy and forces between atoms [38].
TIP3P / SPC/E Water Model	Solvent	Explicit solvent model representing water molecules in the system, crucial for simulating a physiological environment.
GRGMACS / NAMD / AMBER	MD Engine	Software package that performs the numerical integration of Newton's equations of motion and calculates forces.
Graphics Processing Unit (GPU)	Hardware	Specialized hardware that dramatically accelerates the computation of non-bonded interactions, making longer simulations feasible [33].

Limitations, Challenges, and Future Directions

Despite its power, the MD method has important limitations. The accuracy of any simulation is fundamentally limited by the force field [32]. Classical force fields use fixed atomic charges and cannot model chemical reactions where bonds form or break; such processes require hybrid QM/MM (Quantum Mechanics/Molecular Mechanics) methods [33]. The timescale barrier is another major challenge, as many biologically important events (e.g., full protein folding, large conformational changes in enzymes) occur on millisecond to second timescales, while even state-of-the-art simulations are typically limited to microseconds [32] [33].

A significant conceptual challenge, highlighted in recent critical assessments, is that MD simulations and AI-based structure prediction tools like AlphaFold often rely on static structures determined in non-physiological conditions (e.g., X-ray crystallography) [17] [37]. This creates a potential disconnect from the true, dynamic, and environmentally-sensitive functional structure of proteins in solution, a concept analogous to the Heisenberg Uncertainty Principle in quantum mechanics, where the act of measurement (structure determination) can perturb the system [17].

Future developments are focused on creating more accurate and polarizable force fields, harnessing exascale computing to access longer timescales, and developing enhanced sampling methods to more efficiently explore complex energy landscapes [33] [35]. The integration of MD with experimental data from techniques like cryo-EM, NMR, and single-molecule force spectroscopy (e.g., magnetic tweezers) will be crucial for validating simulations and building models that truly capture the dynamic reality of biological molecules [19].

Molecular Dynamics, powered by empirical force fields, has firmly established itself as an indispensable computational microscope. It provides a unique, atomic-resolution view of biological processes in motion, offering a powerful framework to confront fundamental problems like Levinthal's paradox. By simulating the physical forces that guide a protein along its folding funnel and through its functional conformational ensemble, MD moves beyond static snapshots to a dynamic understanding of biomolecular function. While challenges in accuracy, timescale, and the representation of the native biological environment remain, ongoing advances in force field design, computational hardware, and integrative modeling ensure that MD will continue to be a cornerstone technique for researchers and drug developers seeking to understand and manipulate the machinery of life at the atomic level.

The process of protein folding, whereby an amino acid chain adopts its unique, functional three-dimensional structure, occurs on timescales of microseconds to minutes. This presents a fundamental paradox, as a random search of all possible conformations would take an astronomically longer time. This is the essence of Levinthal's paradox, which has historically framed the protein folding problem [17]. The resolution lies not in a random search but in the presence of a biased energy landscape, where the protein is funneled towards its native state. The actual transition from the unfolded to the folded state is not a gradual shift but a stochastic process where the protein must surmount a free energy barrier. The fleeting event of crossing this barrier is the transition path [39].

Understanding the transition path is critical for a complete molecular understanding of folding and function. Direct experimental observation of these paths provides a window into the dynamics of barrier crossing, a process central to chemical reactions, molecular recognition, and, by extension, rational drug design [39] [40]. Modern molecular dynamics (MD) simulations have become indispensable tools for investigating these phenomena, allowing researchers to capture the continuous conformational changes and transient states that are challenging to observe experimentally [41] [40]. This guide delves into the quantitative characterization, methodologies, and research tools for capturing and analyzing these critical transition paths.

Quantitative Characterization of the Transition Path

The transition path (TP) is formally defined as the piece of a molecular trajectory that begins when the system enters a predefined transition region from the reactant state (e.g., unfolded) and ends when it exits to the product state (e.g., folded), without recrossing the boundaries [39]. Several key metrics are used to quantify its properties.

Key Transition Path Metrics and Formulations

Table 1: Core Quantitative Definitions for Transition Path Analysis.

Metric	Mathematical Definition	Physical Interpretation
Transition Path Time (TPT)	( t_{TP} )	The mean temporal length of a transition path; the direct transit time between state boundaries [39].
Transition Path Velocity ((v_{TP}(x)))	( \frac{1}{v{TP}(x)} = \lim{\Delta x \to 0} \frac{\Delta t(x-\Delta x/2, x+\Delta x/2)}{\Delta x} )	An effective local velocity defined by the cumulative residence time in an interval, not the instantaneous speed. It preserves statistical information about recrossings [39].
Reactive Flux	( F{A \to B} = v{TP}(x) p_{eq}(x) P(TP \mid x) )	The exact, local expression for the equilibrium unidirectional flux from state A to state B, which is independent of the coordinate ( x ) [39].
Exact Transition Rate	( k{A \to B} = PA^{-1} v{TP}(x) p{eq}(x) P(TP \mid x) )	A generalization of Transition State Theory that uses the transition-path velocity to provide the exact transition rate, accounting for dynamics [39].

Insights from Simulation Data

Molecular dynamics simulations provide numerical insights into these quantities. For instance, a 12.6 μsec simulation of a 20-residue triple-stranded β-sheet peptide (Beta3s) revealed key statistics of the folding process, demonstrating the efficiency of the search on a biased energy landscape [41].

Table 2: Representative Transition Path Data from MD Simulations of Beta3s Folding [41].

Parameter	Value from Beta3s Simulation	Context and Significance
Total Simulation Time	12.6 μsec	Much longer than the system's relaxation time, ensuring adequate sampling of folding/unfolding events.
Average Folding Time	~85 nsec	Similar to the unfolding time at the melting temperature, indicating equal population of states.
Clusters Sampled During a Folding Event	< 400	A minute fraction of the total conformers in the denatured state, illustrating a directed, non-random search.
Total Conformers (Cluster Centers) in Denatured State	> 15,000	Highlights the vastness of the unfolded state ensemble, consistent with the underlying premise of Levinthal's paradox.

Methodologies for Capturing and Analyzing Transition Paths

Experimental and Computational Workflows

Studying transition paths requires a combination of high-resolution experimental techniques and sophisticated computational simulations. The following diagram outlines a generalized, integrated workflow for these studies.

Diagram 1: Workflow for Transition Path Analysis.

Detailed Experimental Protocols

Single-Molecule Force Spectroscopy for Transition Path Observation

This protocol details the process for using force spectroscopy to directly observe transition paths in protein folding, as referenced in studies of protein and DNA dynamics [39].

• Core Principle: A single protein is tethered between two microscopic beads or a bead and a surface. Controlled forces are applied, and the molecule's extension, ( x(t) ), is measured as it fluctuates and transitions between folded and unfolded states.
• Key Steps:
  • Sample Preparation: The protein of interest is engineered to include specific handles (e.g., biotin or digoxigenin) at its termini for attachment to functionalized beads or surfaces.
  • Instrument Setup: The experiment is conducted using an atomic force microscope (AFM) or optical tweezers apparatus. The molecule is stretched to a force where folded and unfolded states have similar probabilities, maximizing the chance of observing transitions.
  • Data Acquisition: The extension ( x(t) ) is recorded at the highest possible temporal resolution (current best is ~1 μs). The recorded signal is a smoothed version of the true molecular motion due to instrumental limitations.
  • Transition Path Identification: The trajectory is analyzed to identify segments where the extension crosses from a value characteristic of the unfolded state (( xA )) to one characteristic of the folded state (( xB )), without recrossing. These segments are the experimentally observed transition paths.
  • Velocity Calculation: The effective transition-path velocity, ( v_{TP}(x) ), is calculated not from instantaneous speed but from the cumulative residence time transition paths spend in small spatial intervals, as defined in Table 1 [39].

Molecular Dynamics Simulations for Transition Path Sampling

MD simulations provide an atomistic view of transition paths, complementing experimental observations. The following protocol is based on simulations of peptides like Beta3s [41] and modern CADD practices [40].

• Core Principle: Newton's equations of motion are numerically solved for all atoms in the system, generating a trajectory that captures spontaneous folding and unfolding events.
• Key Steps:
  • System Setup:
    • Initial Structure: The simulation can be started from the folded state, the unfolded state, or an intermediate.
    • Force Field: Selection of an appropriate molecular mechanics force field (e.g., CHARMM, AMBER) to describe atomic interactions.
    • Solvation: The protein is placed in a box of explicit water molecules or an implicit solvent model to represent the aqueous environment. Implicit solvent can enable longer timescale simulations [41].
    • Neutralization: Ions are added to neutralize the system's charge.
  • Equilibration: The system is energy-minimized and then simulated under stable conditions (e.g., constant temperature and pressure) to reach equilibrium.
  • Production Run: A long, unbiased simulation is performed. For the Beta3s peptide, multiple simulations of ~3 μsec each were run at 330 K (near the melting temperature) to observe reversible folding [41].
  • Trajectory Analysis:
    • Reaction Coordinate: A progress variable like the fraction of native contacts (( Q )) or the root mean square deviation (RMSD) from the native structure is calculated for every frame of the trajectory.
    • Event Detection: Folding events are defined as transitions where ( Q ) crosses a high threshold (e.g., >0.85), and unfolding events where it crosses a low threshold (e.g., <0.15) [41].
    • Cluster Analysis: Structures from the trajectory are grouped into clusters based on structural similarity (e.g., using a Cα RMSD cutoff of 2.0 Ã…) to characterize the diversity of the unfolded state and the structures sampled during a folding event [41].

The Scientist's Toolkit: Research Reagent Solutions

This section details essential computational tools and theoretical models used in transition path research.

Table 3: Essential Resources for Transition Path Research.

Tool / Resource	Type	Function in Research
CHARMM/AMBER	Software (Molecular Dynamics)	Widely used MD simulation packages that perform the calculations to generate atomic-level trajectories of proteins, enabling the observation of spontaneous transition paths [41] [40].
Specialized Hardware (Anton, GPUs)	Hardware	Application-specific integrated circuits (ASICs) and graphics processing units (GPUs) dramatically accelerate MD simulations, making it feasible to reach the microsecond-to-millisecond timescales on which many transitions occur [40].
Implicit Solvent Models	Computational Model	These models replace explicit water molecules with a continuous dielectric, reducing computational cost and allowing for longer simulation times to observe more transition events [41].
Reaction Coordinate (e.g., Q, RMSD)	Analytical Metric	An order parameter that tracks progress along the transition. Monitoring it allows for the identification of transition paths from within a long, complex trajectory [41].
Kramers–Eyring Approximation	Theoretical Model	An refinement of transition state theory that provides a more accurate estimate of the prefactor ( k_0 ) in the rate equation, using the curvature of the potential energy landscape at the minimum and saddle point [42].
Transition Path Velocity ((v_{TP}))	Analytical Metric	An effective velocity that can be measured from low-time-resolution data and is used to express the exact transition rate, bridging the gap between experiment and theory [39].
Hexyl Methanethiosulfonate
Ethyl 3-trifluoromethylpyrazole-4-carboxylate	Ethyl 3-(Trifluoromethyl)pyrazole-4-carboxylate|CAS 155377-19-8

The field of transition path analysis is rapidly advancing, driven by synergies between computation and experiment. The integration of machine learning with molecular dynamics is a particularly promising avenue. Machine learning models can now predict quantum effects that influence ligand binding, guide the selection of simulation frames for more accurate free-energy calculations, and even help generate conformational ensembles from tools like AlphaFold, which can then be refined with MD [40]. Furthermore, the ability to run massively long and large-scale simulations (reaching billion-atom systems) allows researchers to study barrier crossings in increasingly realistic biological environments, such as within macromolecular complexes or crowded subcellular conditions [40].

In conclusion, the concept of the transition path moves beyond the thermodynamic view of barrier crossing to focus on the dynamic, stochastic event itself. By leveraging sophisticated experimental techniques like single-molecule spectroscopy and powerful computational methods like molecular dynamics, researchers can now capture and characterize these brief, critical events. This detailed understanding resolves the conceptual challenges posed by Levinthal's paradox, showing that proteins fold not by exhaustive search but by a biased, funneled exploration of a small subset of conformations on the way to the native state [17] [41]. More importantly, it provides a dynamic foundation for advances in molecular sciences, most notably in the rational design of drugs that can influence the barrier-crossing processes of their targets [40].

For decades, the protein folding problem—predicting a protein's three-dimensional structure from its amino acid sequence—stood as a grand challenge in molecular biology. The Levinthal paradox highlighted the apparent impossibility of this process, noting that a protein cannot possibly sample all possible conformations through a random search, as it would require billions of years, whereas actual folding occurs in milliseconds to seconds [43]. This paradox suggested the existence of specific folding pathways or a biased energy landscape that guides the protein to its native state [44].

This review examines how AlphaFold2 (AF2), a deep learning system developed by DeepMind, has revolutionized this field by leveraging co-evolutionary analysis to achieve unprecedented accuracy in protein structure prediction. By solving the structure prediction problem, AF2 has not only transformed structural bioinformatics but also provided new tools for investigating the fundamental principles of protein folding itself [45] [46].

Theoretical Foundation: Co-evolution as a Structural Guide

The Physical Basis of Co-evolution

The theoretical foundation of AF2 rests upon the principle that amino acids that are spatially close in the folded structure tend to co-evolve. When a mutation occurs in one residue, structural or functional constraints often necessitate compensatory mutations in its interacting partners to preserve the protein's fold and function [47]. This co-evolutionary relationship creates statistical patterns in multiple sequence alignments (MSAs) that can be mined to infer spatial proximity.

AF2 uses a sophisticated neural network architecture to detect these subtle co-evolutionary signals, effectively learning the evolutionary constraints that dictate which residue pairs must be in contact to maintain a stable three-dimensional structure [45] [47]. This approach represents a significant departure from traditional physics-based simulation methods, which often struggled with the computational complexity of molecular simulation and the difficulty of producing sufficiently accurate models of protein physics [45].

Resolving Levinthal's Paradox Through an Energy Landscape Perspective

The solution to Levinthal's paradox lies in understanding that proteins do not fold by random search but rather navigate a funnel-shaped energy landscape where the native state corresponds to the global free energy minimum [43]. This landscape is biased toward the native state, with many parallel routes leading downhill, eliminating the need for a specific, predetermined pathway [44].

Recent evidence suggests that AF2 has internalized aspects of this energy landscape. When operated without multiple sequence alignments (MSAs) in an ab initio mode, AF2 can still navigate toward native-like structures for some proteins, indicating that its network parameters encode an imperfect biophysical scoring function that captures fundamental folding principles [48]. Iterative prediction with AF2 has been shown to produce structures that correspond to experimentally observed folding intermediates, following a "local first, global later" mechanism consistent with theoretical models [48].

The AlphaFold2 Architecture: A Technical Breakdown

Input Representation and Feature Engineering

AF2 requires only the amino acid sequence of the target protein as user input. However, the system internally processes this sequence to generate several sophisticated representations that form the basis for structure prediction [47]:

• Multiple Sequence Alignment (MSA): The input sequence is used to query large genomic databases (e.g., UniRef, BFD) to construct an MSA, which aligns evolutionarily related sequences. A diverse MSA with hundreds or thousands of sequences provides strong co-evolutionary signals, while a shallow MSA often leads to inaccurate predictions [47].
• Pair Representations: AF2 creates a set of pair representations modeling the relationships between every pair of amino acid residues in the protein. These representations initially encode co-evolutionary relationships derived from the MSA but are progressively refined to represent spatial constraints [47].

Table 1: Key Input Components for AlphaFold2 Prediction

Component	Source	Role in Structure Prediction
Amino Acid Sequence	User input	Primary input defining the protein of interest
Multiple Sequence Alignment (MSA)	Generated from sequence databases using the input sequence	Provides evolutionary constraints and co-evolutionary signals
Pair Representation	Derived from MSA and updated throughout processing	Encodes spatial relationships between residue pairs
Templates (Optional)	PDB or experimental structures	Can provide additional structural guidance, though AF2 may ignore them if MSA information is sufficient

The Evoformer: Neural Network Architecture for 3D Reasoning

The Evoformer is the core neural network block of AF2 that jointly processes the MSA and pair representations through a series of transformative operations [45] [47]. Its key innovation is the continuous, bi-directional flow of information between these two representations, enabling simultaneous reasoning about evolutionary relationships and spatial constraints.

The Evoformer employs several specialized operations:

• MSA-to-Pair Information Transfer: An outer product operation sums over the MSA sequence dimension to update the pair representation with co-evolutionary information [45].
• Triangle Multiplicative Updates: These operations enforce geometric consistency within the pair representation by considering triangles of edges involving three different residues, effectively enforcing constraints like the triangle inequality on distances [45].
• Axial Attention Mechanisms: Modified attention mechanisms operate along rows and columns of the MSA representation, biased by information projected from the pair representation [45].

This architecture enables the Evoformer to develop what the original paper describes as a "concrete structural hypothesis" early in processing, which is continuously refined through successive layers [45].

The Structure Module: From Representations to 3D Coordinates

The structure module translates the refined representations from the Evoformer into explicit atomic coordinates for all heavy atoms in the protein [45]. Unlike previous systems that predicted inter-atomic distances or angles, AF2 directly predicts 3D coordinates through an equivariant transformer architecture that respects the geometric symmetries of 3D space [45].

Key aspects of the structure module include:

• It starts with a trivial initialization where all residues are placed at the origin.
• It employs a local refinement strategy that breaks the chain structure to allow simultaneous optimization of all regions.
• It uses a rigid body representation with rotations and translations for each residue.
• The module includes explicit reasoning about unrepresented side-chain atoms to ensure accurate placement [45].

The Recycling Iteration: Iterative Refinement for Accuracy

A critical innovation in AF2 is the recycling mechanism, where the MSA, pair representations, and 3D structure are fed back through the same network multiple times (typically three times) to progressively refine the prediction [45] [47]. This iterative process allows the system to correct initial errors and significantly improves final accuracy, with each recycling step enabling more precise atomic placements and confidence estimates [47].

Diagram 1: AlphaFold2's Overall Workflow with Recycling Mechanism

Quantitative Performance Assessment

CASP14 Benchmark Results

In the Critical Assessment of protein Structure Prediction (CASP14), a blind competition regarded as the gold standard for structure prediction methods, AF2 demonstrated unprecedented accuracy that dramatically outperformed all competing methods [45].

Table 2: CASP14 Performance Metrics for AlphaFold2 vs. Next Best Method

Metric	AlphaFold2 Performance	Next Best Method Performance	Improvement Factor
Backbone Accuracy (median Cα RMSD₉₅)	0.96 Å	2.8 Å	~3x
All-Atom Accuracy (median RMSD₉₅)	1.5 Å	3.5 Å	~2.3x
Comparison Reference	Carbon atom width: ~1.4 Ã…	-	-

The accuracy achieved by AF2 is particularly notable given that the width of a carbon atom is approximately 1.4 Ã…, meaning AF2 predictions approach atomic-level precision [45]. This level of accuracy has been confirmed on large collections of recently released PDB structures, demonstrating that the performance generalizes beyond the CASP assessment [45].

Confidence Calibration: The pLDDT Metric

AF2 provides a per-residue confidence score called predicted local distance difference test (pLDDT), which reliably predicts the local accuracy of the corresponding region of the predicted structure [45]. This confidence metric ranges from 0-100 and enables researchers to identify potentially unreliable regions in predictions. The global accuracy, measured by template modeling score (TM-score), can also be accurately estimated from the prediction [45].

Experimental Protocols for Investigating Folding Principles

Protocol for Identifying Folding Intermediates Using AF2

Recent research has developed methodologies to leverage AF2 for investigating protein folding pathways and intermediates [48]:

• Input Preparation: Use the wild-type amino acid sequence without multiple sequence alignments (MSAs) or initial templates.
• Iterative Prediction:
  • Perform an initial structure prediction using only the sequence.
  • Use the predicted structure as a template for the next iteration.
  • Combine with AF2's internal recycling mechanism (typically 3 cycles).
• Convergence Monitoring: Continue iterations until convergence of both structure prediction and confidence scores (pLDDT).
• Intermediate Analysis: Structures generated along the iterative prediction pathway are analyzed as potential folding intermediates.

This approach forces AF2 to sample its entire learned energy landscape rather than relying on co-evolutionary signals to navigate to a narrow region, making it more akin to traditional ab initio methods [48].

Validation Against Experimental Folding Data

When applied to proteins with well-characterized folding pathways (protein G, protein L, ubiquitin, and SH3 domain), this iterative AF2 protocol generated intermediate structures in excellent agreement with experimental data from Ï•-value analysis and molecular dynamics simulations [48]. Key findings include:

• AF2 correctly identified pathway differences between protein G and protein L, despite their similar topologies.
• The system detected altered folding routes in mutant sequences (protein Gmut and protein Lmut).
• For ubiquitin, AF2 predicted early formation of an N-terminal hairpin, with sampling of different C-terminal conformations before establishing correct end-to-end contacts.
• For the SH3 domain, the method preserved the middle three β-strands early, with N- and C-terminal contacts forming later.

These results demonstrate AF2's capacity to capture intricate folding pathways and its sensitivity to sequence changes that alter folding mechanisms [48].

Diagram 2: Experimental Protocol for Folding Intermediate Identification

Table 3: Essential Research Resources for AlphaFold2-Based Structural Biology

Resource Type	Specific Examples	Function and Application
Sequence Databases	UniProt, UniRef, BFD	Provide evolutionary related sequences for constructing multiple sequence alignments (MSAs)
Structure Databases	Protein Data Bank (PDB)	Source of experimental structures for validation and template-based modeling
Computational Frameworks	AlphaFold2 Open Source Code, ColabFold	Implement the core AF2 algorithm with varying hardware requirements and accessibility
Validation Tools	pLDDT, predicted TM-score, MolProbity	Assess prediction quality and structural reliability
Specialized Applications	AF2Cluster, ProteinMPNN	Extend AF2 for specific applications like conformational sampling or protein design

Applications in Drug Discovery and Molecular Dynamics

The impact of AF2 extends far beyond basic structural biology into applied pharmaceutical research:

• Target Identification and Validation: AF2 enables rapid structural characterization of potential drug targets, even for proteins with no experimentally solved structures [49] [46].
• Drug Design and Screening: Accurate protein structures facilitate virtual screening of compound libraries and structure-based drug design [49].
• Understanding Disease Mechanisms: AF2 models help elucidate structural impacts of mutations in genetic diseases [46].
• Accelerating Research Timelines: The AlphaFold Protein Structure Database provides immediate access to predicted structures for the entire human proteome and numerous model organisms, dramatically reducing the time from target identification to drug candidate optimization [46].

In molecular dynamics research, AF2 has provided high-quality starting structures for simulations and offered new approaches for investigating folding pathways through iterative prediction protocols [48]. While AF2 produces static structures, its emerging applications in intermediate identification create bridges to the dynamic realm of folding kinetics traditionally studied through MD simulations [48].

AlphaFold2 represents a paradigm shift in structural biology, demonstrating that deep learning systems can extract sufficient information from evolutionary relationships to predict protein structures with experimental accuracy. By leveraging co-evolutionary analysis through its novel Evoformer architecture, AF2 has effectively solved the long-standing protein structure prediction problem.

The system's implications for understanding Levinthal's paradox are profound. Evidence that AF2 can navigate toward native-like structures even without co-evolutionary signals suggests it has learned fundamental principles of protein folding energetics [48]. The iterative prediction protocol provides a new computational tool for generating testable hypotheses about folding pathways and intermediates.

Future developments will likely focus on overcoming current limitations, including modeling conformational flexibility, protein-protein interactions, and the effects of post-translational modifications [46]. As these challenges are addressed, the integration of AF2 with experimental structural biology and drug discovery pipelines will continue to deepen, further accelerating our understanding of protein function and therapeutic development.

The field of protein science is undergoing a fundamental paradigm shift, moving beyond static structural representations toward a dynamic understanding of conformational ensembles. While breakthroughs like AlphaFold have revolutionized static structure prediction, they face inherent limitations in capturing the essential dynamics governing protein function. This whitepaper examines contemporary computational approaches for predicting conformational ensembles, framed within the historical context of Levinthal's paradox and advanced molecular dynamics research. We provide a technical analysis of ensemble generation methodologies, detailed experimental protocols, and practical toolkits for researchers. By integrating insights from artificial intelligence, molecular simulations, and biophysical theory, we demonstrate how the conceptual resolution of Levinthal's paradox through energy landscape theory directly informs modern ensemble-based approaches, offering transformative potential for drug discovery and therapeutic development.

The protein folding problem, once dominated by Levinthal's paradox, has evolved to address the challenge of conformational heterogeneity. Levinthal's paradox highlights the astronomical number of possible conformations a protein could theoretically adopt, making a random search for the native state implausible within biologically relevant timescales [14]. This paradox finds resolution in the concept of a funneled energy landscape where proteins do not randomly sample all possible configurations but are guided toward the native state through biased pathways [50] [44] [14].

The historical focus on single, static structures—exemplified by Anfinsen's dogma and advanced through deep learning systems like AlphaFold—has provided crucial foundations but presents limitations for understanding biological function [51] [37]. Proteins are inherently dynamic entities that sample multiple conformational states under physiological conditions [51] [52]. This conformational ensemble—the collection of structures a protein adopts under given conditions—mediates virtually all biological functions, from enzyme catalysis to signal transduction [51].

The post-AlphaFold era has witnessed a deliberate shift from single-structure to multi-state representations, acknowledging that protein function is "fundamentally governed by dynamic transitions between multiple conformational states" [51]. This transition is crucial for addressing the limitations of static structure prediction, particularly for intrinsically disordered proteins (IDPs) comprising 30-40% of the human proteome and challenging targets in drug discovery [53] [54].

Methodological Approaches for Ensemble Prediction

Current computational approaches for predicting conformational ensembles integrate diverse methodologies ranging from molecular dynamics to artificial intelligence, each with distinct strengths and limitations for sampling conformational space.

AI-Based Ensemble Methods

AlphaFold-derived sampling strategies modify input parameters—including multiple sequence alignment (MSA) masking, subsampling, and clustering—to capture different co-evolutionary relationships and generate diverse conformations [51]. Recently, generative models leveraging diffusion and flow matching techniques have emerged as powerful tools for predicting multiple conformations by transforming structure prediction into sequence-to-structure generation through iterative denoising [51].

The FiveFold methodology represents a paradigm-shifting ensemble approach that combines predictions from five complementary algorithms (AlphaFold2, RoseTTAFold, OmegaFold, ESMFold, and EMBER3D) to generate conformational landscapes [53] [54]. This framework employs two innovative components: the Protein Folding Shape Code (PFSC) system, which provides standardized representation of secondary and tertiary structure, and the Protein Folding Variation Matrix (PFVM), which systematically captures and visualizes conformational diversity [53].

Physics-Based Simulation Methods

Molecular dynamics (MD) simulations directly simulate physical movements of molecular systems, providing atomistic insights into conformational transitions [51]. Enhanced sampling algorithms address timescale limitations through techniques such as metadynamics and On-the-fly Probability Enhanced Sampling (OPES) that accelerate exploration of conformational space [50].

Advanced collective variable (CV) design explicitly captures critical microscopic interactions, including local hydrogen bonding (distinguishing protein-protein from protein-water interactions) and side-chain packing, while accounting for both native and non-native contacts [50]. This bottom-up strategy builds bioinspired CVs that effectively resolve complex free-energy landscapes and reveal critical intermediates like the dry molten globule state [50].

Table 1: Comparison of Computational Approaches for Conformational Ensemble Prediction

Method	Approach Type	Strengths	Limitations	Representative Tools
AI-Based Ensemble Methods	Statistical learning from structural databases	High speed for well-folded proteins; leverages evolutionary information	Limited for novel folds; dependent on training data diversity	FiveFold, AlphaFold2 with MSA sampling, Diffusion models
Molecular Dynamics	Physics-based simulation	Atomistic detail; models physicochemical environment	Computationally expensive; limited timescales	GROMACS, AMBER, OpenMM, CHARMM
Enhanced Sampling	Accelerated physics-based simulation	Efficient exploration of free energy landscapes; identifies intermediates	Requires careful CV selection; potential for bias	Metadynamics, OPES, OneOPES
Hybrid Quantum-Classical	Quantum computing	Fundamental physics; parallel conformation exploration	Early development; limited to small peptides	VQE, QAOA

Experimental Protocols and Workflows

FiveFold Ensemble Generation Protocol

The FiveFold methodology generates conformational ensembles through a systematic workflow that transforms sequence information into multiple plausible structures [53] [54]:

• Input Processing: A single amino acid sequence serves as input for all five component algorithms (AlphaFold2, RoseTTAFold, OmegaFold, ESMFold, and EMBER3D), eliminating MSA dependency limitations.

• Parallel Structure Prediction: Each algorithm generates independent structural predictions using distinct methodological approaches:

  • AlphaFold2 and RoseTTAFold utilize MSA-based deep learning for long-range contacts
  • OmegaFold, ESMFold, and EMBER3D employ single-sequence methods for orphan sequences

• Structural Feature Encoding: All predicted structures are converted into standardized Protein Folding Shape Code (PFSC) strings, where specific characters represent folding elements (H: alpha helices, E: extended beta strands, B: beta bridges, G: 3₁₀ helices, I: Ï€ helices, T: turns, S: bends, C: coil/loop regions).

• PFVM Construction: The Protein Folding Variation Matrix is assembled by analyzing local structural preferences across all five algorithms for each 5-residue window, capturing position-specific variability and generating probability matrices for each secondary structure state.

• Conformational Sampling: User-defined selection criteria (minimum RMSD between conformations, secondary structure content ranges) guide probabilistic sampling of secondary structure state combinations from the PFVM, ensuring diversity across conformational space.

• Structure Construction and Validation: Each selected PFSC string is converted to 3D coordinates through homology modeling against the PDB-PFSC database, followed by stereochemical validation and quality filtering.

This protocol explicitly addresses Levinthal's paradox by demonstrating how the "astronomical number of conformations for each protein is able to be explicitly obtained from its PFVM" [52].

Workflow of the FiveFold ensemble generation methodology

Enhanced Sampling with Collective Variables

Advanced enhanced sampling protocols employ specifically designed collective variables to overcome timescale limitations in molecular dynamics simulations [50]:

• Feature Identification: Automatically collect bioinspired features from short unbiased trajectories of end states (folded and unfolded), focusing on:

  • Hydrogen bonding patterns distinguishing protein-protein from protein-water interactions
  • Side-chain packing contacts encoding compactness
  • Both native and non-native contacts to enhance state resolution

• Feature Selection: Filter features using a Linear Discriminant Analysis (LDA)-like criterion that maximizes separation between folded and unfolded states while capturing relevant intermediates.

• CV Construction: Build two complementary CVs through intuitive linear combination of selected features with unitary coefficients:

  • A hydrogen bonding CV explicitly capturing angular information and solvent interactions
  • A contact-based CV encoding mesoscale compactness through side-chain interactions

• Enhanced Sampling Execution: Apply constructed CVs within enhanced sampling algorithms (OneOPES), running multiple replicas to ensure reproducible convergence.

• Free Energy Analysis: Reconstruct multidimensional free energy landscapes from simulation data, identifying metastable intermediates and transition states through statistical analysis.

This protocol has successfully resolved complex folding landscapes for mini-proteins like Chignolin and TRP-cage, revealing critical intermediates such as the dry molten globule with agreement to reference data from extensive unbiased simulations [50].

Table 2: Essential Resources for Conformational Ensemble Research

Resource	Type	Function	Access Information
ATLAS Database	MD Database	Comprises simulations of ~2000 representative proteins	https://www.dsimb.inserm.fr/ATLAS [51]
GPCRmd	Specialized MD Database	Focuses on GPCR family transmembrane proteins	https://www.gpcrmd.org/ [51]
SARS-CoV-2 DB	MD Database	Includes simulation trajectories of coronavirus proteins	https://epimedlab.org/trajectories [51]
GROMACS	Simulation Software	Molecular dynamics package for enhanced analysis	Open source package [51]
AMBER	Simulation Software	Suite of biomolecular simulation programs	Commercial and academic versions [51]
OpenMM	Simulation Software	Toolkit for molecular simulation with hardware acceleration	Open source package [51]
PFSC System	Analytical Framework	Standardized representation of protein folding patterns	Described in [52] [53]
OneOPES	Enhanced Sampling	Hybrid sampling scheme exploiting OPES Explore	Algorithm described in [50]

Visualization of Protein Energy Landscapes

The conceptual resolution to Levinthal's paradox lies in the energy landscape theory, which illustrates how proteins navigate conformational space not through random search but through biased, funneled pathways toward the native state.

Protein folding energy landscape with intermediates

This visualization embodies the modern understanding of Levinthal's paradox, where the "folding probability landscape must resemble a rugged funnel that is largest in the entropic unfolded basin and becomes narrower and narrower as one approaches the folded state" [50]. The landscape depicts multiple metastable intermediates and transition states that proteins navigate during folding, rather than undertaking an astronomical random search.

Discussion and Future Perspectives

The integration of ensemble approaches represents a fundamental advancement in structural biology, moving beyond the limitations of single-structure paradigms. As the field progresses, several emerging trends promise to further enhance our understanding of protein dynamics:

Multiscale modeling combining AI-based predictions with physical simulations offers promise for capturing both rapid conformational fluctuations and rare transitions [51] [50]. Quantum computing approaches reframe folding as ground-state optimization problems, using variational algorithms to find lowest-energy configurations, though currently limited to small peptides [55]. Experimental integration with techniques like hydrogen-deuterium exchange mass spectrometry (HDX-MS) and single-molecule FRET provides crucial validation for computational ensembles [51] [17].

The implications for drug discovery are profound, as ensemble-based approaches enable targeting of previously "undruggable" proteins with conformational flexibility, potentially expanding the targetable proteome beyond the current estimated 20% of human proteins [53] [54]. By embracing protein dynamics through conformational ensemble prediction, structural biology addresses the fundamental challenge articulated by Levinthal's paradox while opening new frontiers for therapeutic intervention.

Navigating Computational Limits: Overcoming Sampling and Force Field Challenges

The fundamental challenge in molecular dynamics (MD) simulations, often termed the "timescale dilemma," finds its roots in Levinthal's paradox. In 1968, Cyrus Levinthal noted that if a protein were to fold by randomly sampling all possible conformations, it would require a time longer than the age of the universe [56] [44]. This paradox highlights the stark contrast between astronomical computational timescales and biologically relevant timescales, a discrepancy that extends beyond protein folding to virtually all biomolecular processes. The core of the problem lies in the rough energy landscapes of biomolecules, which are characterized by numerous local minima separated by high energy barriers [57]. Crossing these barriers with conventional MD simulations is computationally prohibitive because simulations can become trapped in local minima, failing to sample all functionally relevant conformations [57].

This sampling inadequacy severely limits the predictive power of MD simulations. As evidenced by research exploring the "Levinthal limit," proteins can inhabit numerous non-native conformations that are thermodynamically as stable as the native state, yet conventional MD struggles to characterize these alternative states adequately [58]. Enhanced sampling methods have therefore emerged as essential computational strategies designed to accelerate the exploration of configuration space systematically. By enhancing the sampling of rare events, these methods allow researchers to bridge the gap between computationally accessible timescales and the timescales governing critical biological phenomena, thus providing a practical resolution to the Levinthal paradox for simulation science [56] [57].

Enhanced sampling methods operate on the principle of modifying the effective energy landscape to facilitate barrier crossing. They can be broadly categorized into methods that rely on collective variables (CVs) and those that do not. The choice of method is critically dependent on the biological question, system size, and prior knowledge of the slow degrees of freedom [57].

Table 1: Key Enhanced Sampling Methods and Their Characteristics

Method	Core Principle	Key Advantages	Ideal for Studying
Replica-Exchange MD (REMD) [57]	Parallel simulations at different temperatures (or Hamiltonians) exchange configurations.	Avoids getting trapped in local minima; no need to predefine reaction coordinates.	Protein folding, peptide aggregation, absolute binding free energies.
Metadynamics [57] [59]	History-dependent bias potential ( "computational sand") is added to CVs to discourage revisiting states.	Explores and directly calculates free energy surfaces; good for complex transitions.	Conformational changes, ligand unbinding, protein-protein interactions.
Adaptive Biasing Force (ABF) [59]	Directly estimates and applies a bias to counteract the mean force along a CV.	Efficiently achieves uniform sampling along pre-defined CVs.	Ion permeation through channels, large-amplitude conformational shifts.
Markov State Models (MSMs) [56]	Many short, independent simulations are aggregated to build a kinetic network model of states.	Provides both thermodynamic and kinetic information; highly parallelizable.	Protein folding pathways, allosteric mechanisms, large conformational changes.
Simulated Annealing [57]	System temperature is gradually lowered from a high value to explore space and find minima.	Effective for finding low-energy structures, including global minima.	Protein structure prediction, refinement, and characterization of flexible systems.

The mathematical foundation of many CV-based methods lies in the definition of the free energy surface. For a collective variable ( \xi ), the Helmholtz free energy ( A ) is given by: [ A(\xi) = -k{\text{B}}T \ln(p(\xi)) + C ] where ( k{\text{B}} ) is Boltzmann's constant, ( T ) is temperature, ( p(\xi) ) is the probability density along the CV, and ( C ) is a constant [59]. By biasing the simulation to flatten this free energy landscape, these methods force the system to explore states that would be otherwise inaccessible.

Detailed Experimental and Computational Protocols

Protocol 1: Metadynamics for Ligand-Protein Unbinding

Objective: To quantify the free energy landscape and identify intermediate states during ligand unbinding from a protein active site.

• System Preparation: Solvate the protein-ligand complex in an explicit water box (e.g., TIP3P model). Add ions to neutralize the system's charge. Employ tools like tleap (Amber) or grompp (GROMACS) for parameterization using a force field such as AMBER or CHARMM [58].
• Equilibration: Minimize the system's energy to remove steric clashes. Perform gradual heating to the target temperature (e.g., 300 K) under an NVT ensemble, followed by equilibrium density adjustment under an NPT ensemble (1 atm) for at least 100 ps.
• Collective Variable (CV) Selection: Define CVs that describe the unbinding process. Typical choices include:
  • CV1: Distance between the protein's binding site residue (e.g., Cα atom) and the ligand's center of mass.
  • CV2: Ligand Solvation Number quantifying the number of water molecules within a sphere around the ligand.
• Metadynamics Simulation: Implement Well-Tempered Metadynamics using a tool like PySAGES [59] or PLUMED. Key parameters include:
  • Gaussian Height: Initial energy hill height (e.g., 1.0 kJ/mol).
  • Gaussian Width: Standard deviation for each CV (determined from preliminary unbiased simulation).
  • Pace: Frequency of Gaussian deposition (e.g., every 500 steps).
  • Biasfactor: Typically between 10-100 to regulate the exploration.
• Analysis: The free energy surface (FES) is reconstructed from the deposited bias potential. Identify metastable states as local minima on the FES and the unbinding barrier as the highest point along the lowest-energy path between bound and unbound states.

Protocol 2: Constructing a Markov State Model (MSM) for Protein Folding

Objective: To elucidate the kinetic pathways and metastable states involved in protein folding.

• Data Generation: Perform hundreds to thousands of short (nanosecond-scale) MD simulations initiated from diverse conformations (e.g., unfolded states, native state, etc.). This is highly amenable to parallel computing on GPU clusters [56].
• Featurization: Extract geometric features from each simulation frame that may correlate with the folding reaction. Common features include:
  • Inter-atomic distances within the protein.
  • Root Mean Square Deviation (RMSD) to native and unfolded structures.
  • Radius of Gyration.
  • Contact maps between residues.
• Dimensionality Reduction and Clustering: Use time-lagged independent component analysis (tICA) or a deep learning-based autoencoder to project the high-dimensional feature data into 2-3 slowest collective variables [60]. Cluster the projected data into discrete microstates using algorithms like k-means.
• Model Building and Validation: Count transitions between microstates at a specified lag time (( \tau )) to build a transition count matrix. Estimate the transition probability matrix to construct the MSM. Validate the model by checking the agreement between implied timescales and the MSM lag time and by comparing model-predicted properties with simulation data [56].
• Analysis: Analyze the MSM as a kinetic network to identify major folding pathways, metastable states (by performing Perron Cluster Cluster Analysis), and calculate folding rates and free energies.

Protocol 3: Replica-Exchange MD (REMD) for Peptide Folding

Objective: To enhance conformational sampling of a small peptide and determine its dominant folded state(s).

• Replica Setup: Typically, 24-64 replicas are set up, each simulating the same system at a different temperature. Temperatures should be exponentially spaced between 300 K and a maximum temperature (e.g., 500 K) where the peptide remains stable but unfolds rapidly [57].
• Simulation and Exchange: Run MD simulations for all replicas in parallel. Periodically (e.g., every 1-2 ps), attempt an exchange of coordinates between neighboring replicas ( i ) and ( j ) with temperatures ( Ti ) and ( Tj ). The exchange is accepted with a probability based on the Metropolis criterion: [ P = \min\left(1, \exp\left[ \left(\frac{1}{kB Ti} - \frac{1}{kB Tj}\right)(Ui - Uj) \right] \right) ] where ( Ui ) and ( Uj ) are the potential energies of the two replicas [57].
• Analysis: The trajectory at the target temperature (300 K) is analyzed for structural properties. The weighted histogram analysis method (WHAM) can be used to calculate the free energy profile as a function of relevant reaction coordinates, such as RMSD or the number of native contacts.

Signaling Pathways, Workflows, and Logical Relationships

The Scientist's Toolkit: Essential Research Reagents and Software

Table 2: Key Software Tools and Their Applications in Enhanced Sampling

Tool / "Reagent"	Type	Primary Function	Application Example
GROMACS [57] [58]	MD Engine	High-performance MD simulations, includes some enhanced sampling methods.	Running the underlying molecular dynamics for REMD simulations.
PySAGES [59]	Sampling Library	Provides a unified, GPU-accelerated interface for multiple advanced sampling methods.	Implementing Metadynamics or ABF with custom CVs in HOOMD-blue or OpenMM.
PLUMED [59]	Sampling Plugin	A widely used library for enhancing sampling and analyzing MD trajectories.	Calculating CVs and adding biases in GROMACS or LAMMPS simulations.
Markov Modeling Libraries (e.g., MSMBuilder, PyEMMA)	Analysis Library	Tools for building and validating Markov State Models from MD data.	Featurization, tICA, and MSM construction from thousands of short simulations.
AMBER [58]	MD Suite	A package for biomolecular simulation, with tools for system setup (LEAP) and analysis.	Parameterizing the system and preparing initial structures for REMD.
GPU Computing Cluster	Hardware	Massively parallel processing hardware essential for long or parallel simulations.	Running hundreds of simultaneous simulations for MSM construction or REMD.
4-Chloro-2-nitrobenzaldehyde	4-Chloro-2-nitrobenzaldehyde, CAS:5551-11-1, MF:C7H4ClNO3, MW:185.56 g/mol	Chemical Reagent	Bench Chemicals
5-Bromo-6-chloropyridine-3-sulfonyl chloride	5-Bromo-6-chloropyridine-3-sulfonyl chloride, CAS:216394-05-7, MF:C5H2BrCl2NO2S, MW:290.95 g/mol	Chemical Reagent	Bench Chemicals

The integration of enhanced sampling methods has fundamentally transformed molecular dynamics from a technique often limited by temporal constraints into a powerful tool for probing long-timescale biological events. Methods such as metadynamics, MSMs, and REMD provide robust computational frameworks to navigate the complex energy landscapes of biomolecules, thereby offering a practical resolution to the timescale dilemma inherent in Levinthal's paradox [56] [57]. The ongoing development of these methods, particularly their coupling with machine learning, is poised to further expand the frontiers of simulation.

The future of enhanced sampling is clearly oriented toward greater automation and integration. We are witnessing the emergence of machine learning force fields (MLFFs) that promise quantum-level accuracy at a classical computational cost, enabling more reliable simulations of complex processes like proton transfer and catalysis [60]. Furthermore, ML is being used to automatically identify optimal collective variables from simulation data and to learn and bias free energy surfaces directly, as seen in methods like artificial neural network sampling implemented in PySAGES [60] [59]. The move toward open-source, GPU-accelerated libraries such as PySAGES ensures that these advanced methodologies are accessible to the broader scientific community, facilitating their application to an ever-widening array of challenging biological problems, from drug discovery to materials design [59].

Force Field Approximations and the Quest for Quantum-Mechanical Accuracy

Molecular dynamics (MD) simulations provide a powerful computational microscope for investigating biological and material systems at the atomic level. The accuracy of these simulations is fundamentally governed by the force field—the empirical potential energy function that describes interatomic interactions. This technical review examines the current landscape of force field approximations, their inherent limitations in achieving quantum-mechanical accuracy, and innovative strategies being developed to bridge this fidelity gap. Within the context of Levinthal's paradox, which highlights the astonishing efficiency of protein folding despite astronomical conformational possibilities, we explore how refined force fields are crucial for simulating complex biomolecular processes. By integrating machine learning approaches, experimental data fusion, and enhanced physical models, the field is progressing toward next-generation force fields capable of delivering quantum-level accuracy across extended spatiotemporal scales.

In the realm of computational chemistry, molecular physics, and molecular modeling, a force field serves as a computational model that describes the forces between atoms within molecules or between molecules as well as in crystals [34]. Essentially, force fields are a variety of interatomic potentials that specify the functional form and parameter sets used to calculate the potential energy of a system at the atomistic level [34]. These models are indispensable for molecular dynamics (MD) or Monte Carlo simulations, enabling researchers to study system behavior over time and explore thermodynamic properties.

The fundamental concept mirrors classical physics force fields but with a crucial distinction: chemical force field parameters describe the energy landscape on the atomistic level, from which acting forces on every particle are derived as gradients of the potential energy with respect to particle coordinates [34]. Force fields exist in specialized forms for diverse materials including organic molecules, ions, polymers, minerals, and metals, with varying functional forms selected based on which atomistic interactions dominate the material behavior [34].

A critical categorization of force fields concerns their representational granularity. All-atom force fields provide parameters for every atom in a system, including hydrogen, while united-atom potentials combine hydrogen and carbon atoms in methyl groups and methylene bridges into single interaction centers [34] [61]. Coarse-grained potentials sacrifice chemical details for computational efficiency, making them particularly valuable for long-time simulations of macromolecules like proteins, nucleic acids, and multi-component complexes [34].

Theoretical Foundations of Force Fields

Fundamental Energy Components

The potential energy in molecular force fields is typically decomposed into bonded and non-bonded interactions, with the general form:

[E{\text{total}} = E{\text{bonded}} + E_{\text{nonbonded}}]

where:

[E{\text{bonded}} = E{\text{bond}} + E{\text{angle}} + E{\text{dihedral}}]

[E{\text{nonbonded}} = E{\text{electrostatic}} + E_{\text{van der Waals}}]

This additive structure enables computational efficiency while capturing essential physics [34] [35].

Bonded Interactions

Bonded interactions describe the energy associated with covalent bond distortions:

• Bond stretching is typically modeled using a harmonic potential approximating Hooke's law:

[E{\text{bond}} = \frac{k{ij}}{2}(l{ij} - l{0,ij})^2]

where (k{ij}) is the bond force constant, (l{ij}) the actual bond length, and (l_{0,ij}) the equilibrium bond length between atoms (i) and (j) [34]. While sufficient near equilibrium, more expensive Morse potentials provide better description at higher stretching and enable bond breaking [34].

• Angle bending describes the energy penalty for deviating from optimal bond angles:

[V{\text{Angle}} = k\theta(\theta{ijk} - \theta0)^2]

where (k\theta) is the angle force constant, (\theta{ijk}) the actual angle, and (\theta_0) the equilibrium angle [35]. Force constants for angle bending are typically about five times smaller than for bond stretching [35].

• Torsional potentials describe rotation around bonds, represented as a periodic function:

[V{\text{Dihed}} = k\phi(1 + \cos(n\phi - \delta)) + \ldots]

where (k_\phi) is the dihedral force constant, (n) the periodicity, (\phi) the dihedral angle, and (\delta) the phase shift [35]. Multiple periodic terms can be summed to reproduce complex rotational energy profiles.

• Improper dihedrals enforce out-of-plane bending, typically using a harmonic function to maintain planarity in aromatic rings and other conjugated systems [35].

Non-Bonded Interactions

Non-bonded interactions operate between atoms not directly connected by covalent bonds:

• Van der Waals forces are most commonly described by the Lennard-Jones potential:

[V_{\text{LJ}}(r) = 4\epsilon\left[\left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^{6}\right]]

where (\epsilon) is the well depth, (\sigma) the van der Waals radius, and (r) the interatomic distance [35]. The (r^{-12}) term describes Pauli repulsion at short distances while the (r^{-6}) term captures attractive dispersion forces.

• Electrostatic interactions follow Coulomb's law:

[E{\text{Coulomb}} = \frac{1}{4\pi\varepsilon0}\frac{qi qj}{r_{ij}}]

where (qi) and (qj) are atomic partial charges, (r{ij}) the distance between atoms, and (\varepsilon0) the vacuum permittivity [34]. These interactions are computationally demanding due to their long-range nature, requiring specialized algorithms like Ewald summation or particle mesh Ewald for accurate treatment [35].

Force Field Classification

Force fields are categorized into classes based on their complexity and physical completeness:

• Class 1 force fields use harmonic bonds/angles and lack cross-terms (AMBER, CHARMM, GROMOS, OPLS) [35]
• Class 2 incorporate anharmonic terms and cross-terms between internal coordinates (MMFF94, UFF) [35]
• Class 3 explicitly include polarization and other electronic effects (AMOEBA, DRUDE) [35]

Force Field Classification Diagram: Categorization of force fields by representational granularity and physical complexity.

Levinthal's Paradox and the Energy Landscape Perspective

The Fundamental Paradox

In 1969, Cyrus Levinthal posed a fundamental question that continues to shape molecular dynamics research: how do proteins fold so rapidly despite the astronomical number of possible conformations? [14] For a polypeptide of 100 residues, with approximately two torsion angles per residue, and assuming each angle could adopt just three stable conformations, the protein could misfold into approximately 3²⁰⁰ (or ~10⁹⁵) different conformations [14]. Even sampling conformations at nanosecond or picosecond rates, a random search would require time longer than the age of the universe to arrive at the correct native conformation—yet most small proteins fold spontaneously on millisecond or even microsecond timescales [14].

This apparent contradiction, known as Levinthal's paradox, highlights the inadequacy of conceptualizing protein folding as a random conformational search. Levinthal himself recognized that proteins must fold through guided pathways, suggesting that "protein folding is sped up and guided by the rapid formation of local interactions which then determine the further folding of the peptide" [14]. This insight anticipated the modern energy landscape theory of protein folding.

The Folding Funnel Hypothesis

The resolution to Levinthal's paradox lies in recognizing that the energy landscape is not flat but funnel-shaped—biased toward the native state through evolutionary selection of amino acid sequences [14]. Rather than searching randomly, folding proceeds through a series of correlated motions where the formation of local structures restricts subsequent conformational choices, dramatically reducing the effective search space.

This conceptual framework has profound implications for force field development: accurate simulation of protein folding requires not just correct representation of the native state, but faithful reproduction of the entire energy landscape—the relative energies of unfolded states, intermediates, and transition states [14] [30]. Inaccuracies in force fields can distort this landscape, either creating deep kinetic traps that slow folding or failing to stabilize the native state sufficiently.

Limitations in Achieving Quantum-Mechanical Accuracy

Parametrization Challenges

Force field parameters are determined through empirical procedures that incorporate data from classical laboratory experiments, quantum mechanical calculations, or both [34]. This parametrization is arguably the most critical factor determining force field accuracy and reliability. Two predominant philosophies guide parametrization:

• Bottom-up approaches derive parameters from quantum mechanical calculations or spectroscopic data, aiming to reproduce quantum-level interactions [62]
• Top-down approaches fit parameters to macroscopic experimental properties like densities, enthalpies of vaporization, and compressibility [62]

Each method presents trade-offs. Bottom-up approaches maintain quantum-mechanical consistency but may propagate systematic errors from quantum methods like Density Functional Theory (DFT), which "are not always in quantitative agreement with experimental predictions" [62]. Top-down approaches better reproduce macroscopic observables but may achieve this through error cancellation, potentially reducing transferability.

The assignment of atomic partial charges exemplifies these challenges. Charges "can make dominant contributions to the potential energy, especially for polar molecules and ionic compounds, and are critical to simulate the geometry, interaction energy, and the reactivity" [34]. However, charge assignment "often follows quantum mechanical protocols with some heuristics, which can lead to significant deviation in representing specific properties" [34].

Several fundamental limitations impede force fields from achieving quantum-mechanical accuracy:

• Fixed charge models in most classical force fields cannot capture electronic polarization, charge transfer, or environment-dependent electronic effects [35]
• Pairwise approximations neglect multi-body interactions, which can be significant in condensed phases [34]
• Functional form limitations, such as harmonic bond potentials, fail under conditions far from equilibrium [34]
• Parameter transferability issues arise when parameters optimized for certain conditions or compounds perform poorly in different environments [34]

Table 1: Comparison of Force Field Approximation Methods

Approximation Type	Common Implementation	Key Limitations	Systems Most Affected
Electrostatics	Fixed point charges, Coulomb's law	Missing polarization, charge transfer	Polar solvents, ionic systems, interfaces
Van der Waals	Lennard-Jones 12-6 potential	Too steep repulsion, poor dispersion	High-pressure systems, dense phases
Bonded Terms	Harmonic bonds/angles	Cannot describe bond breaking	Reactive systems, high temperatures
Solvation	Implicit or explicit solvent models	Missing specific interactions	Biomolecular recognition, self-assembly
Parameterization	Heuristic fitting procedures	Limited transferability	Novel molecules, non-ambient conditions

Machine Learning and Data Fusion Strategies

Machine Learning Force Fields

Machine Learning (ML) force fields represent a paradigm shift in molecular simulations, overcoming the accuracy-efficiency compromise that has limited traditional approaches [62]. While ab initio MD provides high accuracy at low computational efficiency, and classical force fields offer the inverse, ML potentials "can overcome this compromise due to the multi-body construction of the potential energy with unspecified functional form" [62].

ML potentials typically use neural networks or other machine learning architectures to map atomic configurations directly to energies and forces, effectively learning the quantum mechanical potential energy surface from reference data. This approach bypasses the need for pre-specified functional forms, allowing more flexible and accurate representation of complex quantum effects.

Experimental and Simulation Data Fusion

A promising advancement is the fusion of theoretical and experimental data in training ML force fields. Recent research demonstrates that "a concurrent training on the DFT and experimental data can be achieved by iteratively employing both a DFT trainer and an EXP trainer" [62]. This hybrid approach leverages the strengths of both data sources:

• DFT data provides abundant information about quantum mechanical energies, forces, and stresses for diverse atomic configurations [62]
• Experimental data anchors the model to physically measurable properties, correcting systematic errors in the DFT reference [62]

In a case study on titanium, this fused approach yielded an ML potential that "faithfully reproduces all target properties" including temperature-dependent lattice parameters and elastic constants across a wide temperature range (4-973 K) [62]. The method successfully corrected known inaccuracies of DFT functionals while maintaining reasonable performance on off-target properties.

Data Fusion Workflow: Integrated training approach combining DFT and experimental data for ML force field development.

Methodological Protocols for Force Field Development and Validation

Fused Data Learning Methodology

The fused data learning approach demonstrated for titanium provides a generalizable protocol for high-accuracy force field development:

• DFT Database Construction:

  • Generate diverse atomic configurations including equilibrated, strained, and randomly perturbed structures
  • Include configurations from high-temperature MD simulations and active learning approaches
  • Calculate target properties (energy, forces, virial stress) using DFT for each configuration [62]

• Experimental Data Curation:

  • Collect temperature-dependent experimental measurements of key properties (elastic constants, lattice parameters)
  • Select representative temperature points to balance computational cost and temperature transferability [62]

• Alternating Training Protocol:

  • Initialize ML potential parameters using standard DFT-based pre-training
  • Employ iterative training epochs alternating between:
    • DFT trainer: Batch optimization to match DFT-calculated energies, forces, and stresses
    • EXP trainer: Optimization to match experimental properties using Differentiable Trajectory Reweighting (DiffTRe) method [62]
  • Implement early stopping based on validation set performance

• Validation Across Multiple Scales:

  • Assess performance on held-out DFT test datasets
  • Verify reproduction of target experimental properties
  • Evaluate transferability to off-target properties (phonon spectra, different phases, liquid properties) [62]

Advanced Polarizable Force Fields

For Class 3 force fields with explicit polarization, development follows specialized protocols:

• Electronic Structure Calculations:

  • Perform high-level quantum mechanical calculations to parameterize distributed multipoles
  • Determine polarizabilities using response property calculations [35]

• Polarization Model Selection:

  • Drude oscillators: Massless charged particles attached via harmonic springs [35]
  • Inducible point dipoles: Self-consistent dipole iteration at each step [35]
  • Fluctuating charge models: Polarization as charge transfer between atoms [35]

• Many-Body Parameterization:

  • Fit parameters to reproduce interaction energies of molecular clusters
  • Validate against experimental dielectric constants and NMR properties [35]

Table 2: Research Reagent Solutions for Force Field Development

Tool Category	Specific Solutions	Primary Function	Application Context
Quantum Chemistry Software	Gaussian, ORCA, PSI4	Generate reference data for parametrization	Bottom-up force field development
Molecular Dynamics Engines	GROMACS, NAMD, OpenMM, LAMMPS	Run simulations with developed force fields	Validation and production MD
Machine Learning Frameworks	TensorFlow, PyTorch, JAX	Build and train ML force fields	Neural network potential development
Force Field Databases	OpenKIM, MolMod, TraPPE	Access existing parameters	Parameter transfer and comparison
Specialized Analysis Tools	VMD, MDAnalysis, MDTraj	Analyze simulation trajectories	Validation against experimental data

Force field development stands at a transformative juncture, with machine learning approaches and data fusion strategies enabling unprecedented accuracy while maintaining computational efficiency. The longstanding challenge of achieving quantum-mechanical accuracy in classical simulations is being addressed through innovative methodologies that leverage the complementary strengths of theoretical calculations and experimental measurements.

In the context of Levinthal's paradox, these advances promise more realistic simulations of complex biomolecular processes like protein folding, where accurate representation of the energy landscape is essential for capturing the remarkable efficiency of natural folding pathways. As force fields continue to evolve toward quantum-level fidelity, they will expand the horizons of molecular dynamics research, enabling previously intractable investigations into the relationship between molecular structure, dynamics, and function across chemistry, biology, and materials science.

The integration of physical principles with data-driven approaches represents the most promising path forward—developing force fields that are not just parameterized to data, but embody the fundamental physics that govern molecular interactions across multiple spatiotemporal scales.

The field of molecular dynamics (MD) is fundamentally shaped by Levinthal's paradox, which highlights the astronomical number of possible conformations a protein can adopt. In 1969, Cyrus Levinthal noted that a simple polypeptide of 100 residues has an estimated 10³⁰⁰ possible conformations. If it were to sample these sequentially at rapid rates, it would require a time longer than the age of the universe to arrive at its correct native conformation [14]. The paradox is that, in reality, proteins fold spontaneously on millisecond or even microsecond timescales [14]. This implies that protein folding is not a random search but a guided process through an uneven energy landscape, where local interactions and nucleation points steer the folding process [56] [14].

Understanding this process requires simulating molecular motions, a task of immense computational burden. MD simulations model atomic interactions over time, but to capture biologically significant events (like protein folding or drug binding), they must simulate microseconds to milliseconds of molecular time. This necessitates millions of time steps, often taking days or weeks on traditional supercomputers [63]. This review details how specialized hardware, including GPUs and application-specific supercomputers like Anton, are providing unprecedented computational power to resolve this paradox and accelerate biomedical research.

Specialized Supercomputers: The Anton Architecture

D. E. Shaw Research designed the Anton supercomputers as special-purpose systems to overcome the timescale barrier in biomolecular simulation. Unlike general-purpose supercomputers, Anton uses Application-Specific Integrated Circuits (ASICs) tailored for MD, achieving simulation speeds orders of magnitude faster than conventional systems [64] [65].

Architectural Evolution and Performance

Table: Generational Comparison of Anton Supercomputers

Feature	Anton 1 (2008)	Anton 2 (2014)	Anton 3 (2021)
Key Innovation	First dedicated MD ASICs	Improved flexibility & programmability	Tile-based architecture; specialized bond calculators
Reported Speed Gain	~100x vs. contemporary supercomputers [65]	Order of magnitude faster than Anton 1 [65]	Capable of simulating millions of atoms [66]
Biological Impact	Enabled millisecond-scale simulations [65]	Supported 15x more atoms [65]	Simulates large complexes (viruses, ribosomes) [66]
Notable Application	First observations of long-timescale protein dynamics [65]	More accurate physical models [65]	Directly contributed to drugs entering clinical trials [65]

A central architectural principle of Anton is its data-flow design, which minimizes data movement—a major bottleneck in general-purpose systems. Data is preemptively sent to the computational units that need it, bypassing slow trips to a global memory. The inter-chip network is a high-speed, low-latency 3D torus, enabling tight coupling between nodes [64] [65]. Anton 3 introduced a tile-based architecture that combines hardwired pipelines for particle interactions with programmable units, refining this balance further [65].

The impact of this specialized approach is profound. By 2023, simulations on Anton machines had contributed to the development of six drugs in human clinical trials [65]. The ability to run continuous, microsecond-to-millisecond simulations allowed researchers to observe rare biological events, such as the formation of transient cryptic pockets on protein surfaces, which present new therapeutic opportunities [56] [65].

Experimental Protocol for an Anton Simulation

A typical MD experiment on Anton involves a structured pipeline to ensure scientific rigor.

• System Preparation: The protein structure is placed in a simulated water box, ions are added to neutralize the system's charge, and the entire system is energy-minimized and equilibrated to stable temperature and pressure [56].
• Production Simulation on Anton: The equilibrated system is simulated for a defined period, often spanning microseconds. The simulation runs under specific thermodynamic conditions (e.g., NPT ensemble) using Anton's specialized ASICs to calculate forces and update atomic coordinates [66] [65].
• Analysis and Validation: The resulting trajectory is analyzed for properties like root-mean-square deviation (RMSD) or the presence of cryptic pockets. Crucially, findings are validated against experimental data from techniques like hydrogen-deuterium exchange mass spectrometry (HDX-MS) or cryo-electron microscopy (Cryo-EM) [56].

GPU Acceleration in Molecular Dynamics

While Anton provides unparalleled performance for a single application, Graphics Processing Units (GPUs) offer a more accessible and flexible platform for accelerating MD simulations on general-purpose HPC systems.

Hardware Selection and Performance

MD software like AMBER, GROMACS, and NAMD is heavily optimized for NVIDIA GPUs. Performance hinges on CUDA core count and VRAM capacity.

Table: Recommended GPUs for MD Simulations (2024)

GPU Model	Architecture	CUDA Cores	VRAM	Recommended Use Case
NVIDIA RTX 4090	Ada Lovelace	16,384	24 GB GDDR6X	Cost-effective performance for small to medium simulations in GROMACS and NAMD [67].
NVIDIA RTX 6000 Ada	Ada Lovelace	18,176	48 GB GDDR6	Top-tier choice for large-scale, memory-intensive simulations in AMBER [67].
NVIDIA RTX 5000 Ada	Ada Lovelace	~10,752	24 GB GDDR6	Balanced and economical choice for standard simulations [67].

For CPUs, clock speed is often prioritized over core count for many MD workloads. Mid-tier workstation CPUs like the AMD Threadripper PRO 5995WX offer a good balance of high clock speeds and sufficient core count [67]. Multi-GPU setups can dramatically decrease simulation times for complex systems, as software like AMBER and NAMD can distribute computations across several GPUs [67].

Algorithmic Integration: Machine Learning Potentials

A major innovation is the integration of machine learning interatomic potentials (MLIPs) with MD packages like LAMMPS. The ML-IAP-Kokkos interface, for example, allows developers to connect PyTorch-based ML models directly with LAMMPS, enabling scalable simulations on GPUs [68].

The interface uses Cython to bridge Python and C++, ensuring end-to-end GPU acceleration. A key step is implementing the MLIAPUnified class, which defines a compute_forces function. This function is called by LAMMPS during the simulation to infer forces and energies using the native Python ML model, leveraging the full computational power of the underlying GPUs [68].

Emerging Paradigms: Wafer-Scale and Quantum-Hybrid Computing

Beyond established architectures, new computing paradigms are pushing the boundaries of MD.

Wafer-Scale Computing: The Cerebras Wafer-Scale Engine (WSE-3) integrates ~900,000 compute cores on a single silicon wafer. This architecture provides ultra-fast core-to-core communication, making it suitable for MD. In one demonstration, a custom MD engine simulated an antimicrobial peptide (L-K6) at speeds of roughly 10,000 steps per second. This approach shows potential for performing binding free energy calculations—critical in drug discovery—much faster than traditional clusters [63].

Quantum-Classical Hybrid Methods: For simulating quantum mechanical effects (e.g., covalent drug binding), purely classical computers struggle. Hybrid quantum-classical methods offer a solution. In "Project Angelo," researchers use a QM/MM scheme, where most of the system is treated with classical force fields, but the region where a chemical bond forms is treated with quantum mechanics [63].

A practical implementation from a 2025 study combined Density Matrix Embedding Theory (DMET) and Sample-Based Quantum Diagonalization (SQD). This method breaks a large molecule into smaller fragments. A quantum computer (using 27-32 qubits on an IBM device) simulates the chemically relevant fragment, while a classical supercomputer handles the rest. This DMET-SQD approach accurately simulated cyclohexane conformers, with energy differences within 1 kcal/mol of classical benchmarks—a threshold for chemical accuracy [69].

The Scientist's Toolkit: Essential Research Reagents

Table: Key Resources for Advanced Biomolecular Simulation

Resource Category	Specific Tool / Platform	Function / Application
Specialized Hardware	Anton 3 Supercomputer	Millisecond-scale MD of large (million-atom) biological systems [66].
	NVIDIA RTX Ada Generation GPUs	Accelerating MD software (AMBER, GROMACS) on general-purpose HPC systems [67].
	Cerebras Wafer-Scale Engine	Massively parallel MD for ultrafast simulation steps [63].
Software & Algorithms	ML-IAP-Kokkos Interface	Integrating PyTorch-based ML potentials with LAMMPS for GPU-accelerated MD [68].
	Markov State Models (MSMs)	Building network models from MD data to analyze kinetics and thermodynamics [56].
	Density Matrix Embedding Theory (DMET)	Fragmenting large molecules for simulation on quantum computers [69].
Experimental Validation	Hydrogen-Deuterium Exchange (HDX)	Measuring solvent exposure of backbone amides to validate simulated dynamics [56].
	Relaxation Dispersion NMR	Detecting excited protein states with populations as low as 1% [56].
	Cryo-Electron Microscopy (Cryo-EM)	Obtaining high-resolution structures of protein complexes for validation [56].
Methyl 2,2-dimethyl-1,3-dioxolane-4-carboxylate	Methyl 2,2-dimethyl-1,3-dioxolane-4-carboxylate, CAS:108865-84-5, MF:C7H12O4, MW:160.17 g/mol	Chemical Reagent
4-(4-Chlorophenyl)dihydro-2H-pyran-2,6(3H)-dione	4-(4-Chlorophenyl)dihydro-2H-pyran-2,6(3H)-dione, CAS:53911-68-5, MF:C11H9ClO3, MW:224.64 g/mol	Chemical Reagent

The interplay between hardware and algorithmic innovations is fundamentally advancing our ability to model biological macromolecules. Specialized supercomputers like Anton provide a "computational microscope" that has directly visualized protein dynamics processes once thought inaccessible, contributing directly to drug discovery [65]. The widespread adoption of high-performance GPUs has democratized access to powerful MD simulations, a trend accelerated by new software interfaces that integrate machine learning. On the horizon, wafer-scale and hybrid quantum-classical computing offer a glimpse into a future where simulating the intricate dance of atoms in a protein will be faster, more accurate, and capable of tackling ever-larger biological problems. Together, these technologies are not just solving Levinthal's paradox but are also providing a powerful pipeline for the design of new medicines.

The challenge of predicting protein folding and dynamics, famously encapsulated by Levinthal's paradox, presents a fundamental bottleneck in molecular biology and drug discovery. While computational methods like molecular dynamics (MD) simulation can, in principle, reveal atomic-level details of folding pathways, they are often stymied by the vastness of conformational space and the limitations of physical energy functions. This whitepaper details a paradigm shift: the strategic integration of sparse, experimentally-derived data to guide and validate computational simulations. We provide a technical guide on the sources of such data, the computational frameworks capable of assimilating them, and the protocols for their application. By uniting the breadth of simulation with the grounding of experiment, we demonstrate how researchers can overcome the data bottleneck to achieve more accurate, efficient, and biologically relevant predictions of protein structure and function, thereby offering a practical path forward in the context of Levinthal's grand challenge.

In 1969, Cyrus Levinthal observed that a protein cannot possibly sample all possible conformations to find its native structure, as such a systematic search would take longer than the age of the universe [1]. This paradox highlights that protein folding is not a random search but a directed process governed by physical laws and, potentially, evolutionary-shaped folding pathways. For decades, the computational approach to this problem has relied on two pillars: efficient conformational sampling and accurate energy functions [1]. Molecular dynamics (MD) simulations aim to simulate the actual physical process of folding but are often limited to relatively small proteins due to the immense computational cost of simulating the necessary timescales [1] [70].

This reliance on computation alone has inherent limitations. The energy functions used in MD, whether classical or AI-derived, are approximations. Furthermore, as noted in a critical assessment of AI-based protein structure prediction, "the machine learning methods used to create structural ensembles are based on experimentally determined structures of known proteins under conditions that may not fully represent the thermodynamic environment controlling protein conformation at functional sites" [37]. This can lead to inaccuracies in predicting functional states, particularly for proteins with flexible regions or those that are intrinsically disordered.

The integration of sparse experimental data directly into the modeling process breaks this impasse. These data, while incomplete on their own, provide essential distance constraints, topological information, and energetic signatures that can guide computational sampling towards biologically relevant conformations. This guide explores the technical methodologies for achieving this integration, effectively using limited experimental data to solve the high-dimensional problem of protein structure and dynamics.

The Landscape of Sparse Experimental Data

A variety of experimental techniques can generate data suitable for guiding simulations. The key is that these methods do not need to yield a complete atomic-resolution structure; they provide pieces of the puzzle.

Table 1: Key Experimental Techniques Generating Sparse Data for Integration

Technique	Type of Constraint	Typical Resolution/Information	Key Advantage for Integration
Cross-Linking Mass Spectrometry (XL-MS)	Distance Restraint (Residue Pair Restraint - RPR)	Identifies amino acid pairs within a specific distance (e.g., ~10-30 Ã…) [71].	Provides direct, albeit low-resolution, spatial proximity information, ideal for constraining tertiary and quaternary structure.
Deep Mutagenesis Scanning (DMS)	Interface Restraint (IR)	Identifies residues where mutation significantly impacts function or binding, indicating location at an interface [71].	Reveals functional epitopes and critical interaction surfaces without requiring structural data.
Covalent Labeling (CL)	Interface Restraint / Surface Accessibility	Identifies solvent-accessible residues; labeling changes upon binding indicate interface involvement [71].	Probes surface topography and changes upon complex formation.
Chemical Shift Perturbation (CSP) - NMR	Interface Restraint / Structural Environment	Chemical environment changes in NMR spectra indicate residues involved in binding or conformational change [71].	Sensitive probe for subtle structural changes and binding interfaces in solution.
Paramagnetic Relaxation Enhancement (PRE) - NMR	Distance Restraint	Provides long-range distance constraints (up to ~35 Ã…) [71].	Captures long-range interactions and dynamic structural features.

Computational Frameworks for Data Integration

Several advanced computational frameworks have been developed to ingest the experimental data described in Table 1 and use it to guide structure prediction and simulation.

The GRASP Model for Protein Complexes

The GRASP (Geometric Restraints Assisted Structure Prediction) model represents a state-of-the-art approach for integrating diverse experimental data. It is designed specifically for predicting protein complex structures by incorporating two main types of constraints directly into its architecture [71]:

• Residue Pair Restraints (RPR): Derived from methods like XL-MS, these are integrated via the model's Evoformer module and its structure module's invariant point attention (IPA) bias.
• Interface Restraints (IR): Derived from DMS, CL, and CSP, these are introduced through relative position encoding and an "interface fusion block" within the Evoformer and IPA modules [71].

During training, the model's loss function is augmented with terms related to these constraints, forcing the learned patterns to satisfy the experimental observations. Furthermore, GRASP employs an iterative noise filtering strategy during inference to mitigate the impact of erroneous constraints, a critical feature for handling noisy real-world data [71]. Its performance in predicting antigen-antibody complexes, even surpassing AlphaFold3 when using experimental DMS or CL constraints, underscores the power of this integrative approach [71].

Molecular Dynamics with Experimental Biasing

Classical MD can be enhanced by adding bias potentials to the molecular force field that favor conformations satisfying the experimental constraints. For example:

• Distance Restraints: A harmonic potential can be applied between atoms identified by XL-MS or PRE to maintain them within the experimentally determined distance range.
• Chemical Shift Restraints: Potentials can be derived from NMR chemical shifts to bias the simulation towards conformations that reproduce the observed chemical environment.

The core challenge is to balance the physical accuracy of the force field with the experimental biases, ensuring the simulation is guided but not forced into unphysical states. The integration of machine learning is also revolutionizing MD by improving the accuracy of force fields and enhancing the efficiency of conformational sampling [72].

Integrative Modeling Platforms

For the most complex problems, a flexible, multi-stage integrative modeling approach is required. Tools like Combfit can be used in conjunction with prediction models like GRASP to indirectly integrate low-resolution data such as cryo-electron microscopy density maps [71]. This process often involves:

• Generating an ensemble of candidate structures.
• Filtering and scoring these structures against all available experimental data (XL-MS, PRE, mutagenesis, etc.).
• Refining the top-scoring models to obtain a final consensus structure that best satisfies the entire set of sparse data.

Detailed Experimental and Computational Protocols

This section provides actionable methodologies for employing the aforementioned techniques.

Protocol A: Integrating Cross-Linking Mass Spectrometry (XL-MS) Data with GRASP

Objective: To predict the structure of a protein complex using distance constraints from XL-MS.

Materials & Reagents:

• Purified Protein Complex: The target complex for structural analysis.
• Cross-linking Reagent (e.g., BS3): A chemical reagent that forms covalent bonds between proximate amino acids (e.g., lysines).
• Mass Spectrometry System: High-resolution instrument for identifying cross-linked peptides.

Procedure:

• Experimental Data Generation: a. Incubate the purified protein complex with the cross-linking reagent under native conditions. b. Quench the reaction and digest the cross-linked complex with a protease (e.g., trypsin). c. Analyze the digested peptides via liquid chromatography-tandem mass spectrometry (LC-MS/MS). d. Use specialized software (e.g., XlinkX, pLink) to identify the sequences of the cross-linked peptide pairs.

• Data Pre-processing for GRASP: a. Convert identified cross-linked sites into a list of Residue Pair Restraints (RPRs). Each restraint specifies the two residue indices involved. b. Format the RPR list according to GRASP's input requirements (e.g., a simple text file with columns for protein chain, residue number, and paired chain, residue number).

• Computational Modeling with GRASP: a. Configure the GRASP model to run in constrained prediction mode. b. Input the amino acid sequences of the interacting proteins and the RPR list. c. Execute GRASP, which will use the RPRs to guide the structure prediction process, biasing the model towards conformations that satisfy the cross-linking distances. d. The output is a 3D structural model of the complex that is consistent with the experimental XL-MS data.

Protocol B: Using Deep Mutagenesis Scanning (DMS) for Epitope Mapping

Objective: To identify the binding interface (epitope) of an antibody-antigen complex using functional data from DMS.

Materials & Reagents:

• Antigen Library: A comprehensive library of antigen variants, each with a single point mutation.
• Display System (e.g., Yeast Display, Phage Display): A platform for expressing the antigen library and selecting for binding.
• Fluorescently-Labeled Antibody: The antibody whose epitope is being mapped.
• Flow Cytometer or Sequencer: For quantifying the binding of each antigen variant to the antibody.

Procedure:

• Experimental Data Generation: a. Incubate the antigen variant library with the fluorescently-labeled antibody. b. Use fluorescence-activated cell sorting (FACS) or sequencing to quantify the binding enrichment or depletion for each antigen mutant. c. Calculate a binding score for each mutation. Residues where mutation severely disrupts binding are inferred to be part of the functional epitope (Interface Restraint, IR).

• Data Pre-processing for GRASP: a. Generate a list of IRs from the DMS data. This list contains residue indices identified as critical for binding. b. Format the IR list for input to GRASP.

• Computational Modeling with GRASP: a. Input the sequences of the antibody and antigen, along with the IR list. b. GRASP integrates these IRs, using them to ensure the predicted complex structure places these critical residues at the binding interface. c. The output is a structural model where the antigen's binding epitope, as defined by DMS, is correctly positioned against the antibody's paratope.

The following diagram illustrates the logical workflow common to these protocols, showing how sparse experimental data is transformed into structural constraints for computational modeling.

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Computational and Data Resources for Integrative Modeling

Tool / Resource	Type	Primary Function	Relevance to Sparse Data Integration
GRASP	AI-Based Structure Prediction Model	Predicts protein complex structures by directly integrating RPRs and IRs [71].	Core framework for leveraging multiple types of sparse data (XL, DMS, CL, CSP) in a single prediction run.
GROMACS	Molecular Dynamics Simulation Software	Performs high-performance MD simulations to study molecular dynamics [73].	Can be used with biased simulations to incorporate experimental distance or orientation restraints.
Combfit / HADDOCK	Integrative Modeling Platform	Scores and refines structural models against experimental data [71].	Used for combining models from GRASP or other tools with low-resolution data like cryo-EM maps.
LMCache / NVIDIA Dynamo	KV Cache Management System	Manages and offloads large attention (KV) caches during AI model inference [74].	Enables longer context windows and more complex constrained predictions by optimizing memory usage.
PBPK Modeling (e.g., Certara Simcyp)	Physiological Pharmacokinetic Modeling	Simulates drug absorption, distribution, metabolism, and excretion in a virtual human population [75] [76].	Provides a systems-level context for simulating the functional consequences of protein-drug interactions predicted via integrative structural biology.
4-(Boc-amino)tetrahydrothiopyran-4-carboxylic acid	4-(Boc-amino)tetrahydrothiopyran-4-carboxylic acid, CAS:108329-81-3, MF:C11H19NO4S, MW:261.34 g/mol	Chemical Reagent	Bench Chemicals
Ethyl Oleate	Ethyl Oleate | High-Purity Reagent for Research	Ethyl oleate is a high-purity fatty acid ester for research, used as a solvent and vehicle. For Research Use Only. Not for human or veterinary use.	Bench Chemicals

The integration of sparse experimental data represents a powerful and necessary evolution in computational structural biology. It directly addresses the core issue of Levinthal's paradox by providing a "compass" to guide simulations through an otherwise intractable conformational landscape. Frameworks like GRASP demonstrate that this approach is not merely theoretical but can yield state-of-the-art predictions, even outperforming leading ab initio methods when experimental constraints are available [71].

The future of this field lies in several key areas:

• Tighter Integration with Dynamics: Moving beyond static structure prediction to model conformational ensembles and dynamics, acknowledging that "millions of possible conformations... cannot be adequately represented by single static models" [37].
• Automation and "X-as-a-Service": The development of cloud-based platforms and AI-driven tools, such as those proposed for Quantitative Systems Pharmacology (QSPaaS), could make integrative modeling more accessible [77].
• Advanced Computing: Continued performance optimization of simulation software like GROMACS on modern hardware (e.g., ARM architectures) will allow for longer, more complex simulations that can incorporate experimental data in real-time [73].

By embracing the data bottleneck as an opportunity for synergy rather than a limitation, researchers can unlock a deeper, more dynamic understanding of protein function, ultimately accelerating progress in fields like drug discovery and protein engineering.

Benchmarking Predictions: Validating Computational Models Against Experimental Reality

Understanding how proteins fold into their unique three-dimensional structures is a fundamental challenge in molecular biology. The Levinthal paradox highlights the apparent impossibility of proteins searching all possible conformations to find the native state within biologically relevant timescales [44] [41]. This paradox has been resolved by the energy landscape theory, which posits that folding does not occur through a random search but is guided by a funnel-shaped landscape that biases the polypeptide chain toward the native state [78] [44] [41]. Within this framework, the most insightful information about folding mechanisms is contained in the transition path—the brief segment of a molecular trajectory where the free energy barrier is actually crossed between stable states [79] [78]. The transition path represents the crucial "moment of decision" when the protein commits to folding or unfolding, containing all mechanistic information about the self-assembly process [79].

Single-molecule spectroscopy has emerged as a powerful tool for studying these transition paths directly. Unlike ensemble measurements that average over many molecules and obscure individual barrier-crossing events, single-molecule techniques allow observation of individual molecules as they traverse the barrier [78] [80]. This article focuses on how Förster resonance energy transfer (FRET) has been utilized to measure transition path times, providing unprecedented insights into protein folding dynamics and testing fundamental theories against all-atom molecular dynamics simulations [79].

Theoretical Foundations: Defining Transition Paths

What is a Transition Path?

In the context of protein folding, a transition path is formally defined as the segment of a single-molecule trajectory during which the molecule crosses the free energy barrier separating the unfolded (U) and folded (F) states [79] [78]. As illustrated in Figure 1, for a two-state protein, the transition path corresponds to the portion where the molecule leaves a position qU near the unfolded free energy minimum and reaches a position qF near the folded minimum without recrossing qU [79]. This represents the actual barrier-crossing event, distinct from the long waiting periods spent fluctuating within the unfolded or folded basins.

Definition of Transition Path Time

The average transition path time, t~TP~, is the duration of this barrier-crossing segment. Importantly, t~TP~ is the same for both folding and unfolding transitions due to microscopic reversibility [78]. This differs fundamentally from the much longer folding time (t~f~), which represents the average waiting time in the unfolded state before a successful transition to the folded state occurs [79].

Relationship to Kramers' Theory and Energy Landscape

Protein folding is often described as diffusion on a one-dimensional free energy surface [78] [80]. Within this model, Kramers' theory provides relationships for both folding times and transition path times. The folding time is given by:

t~f~ = 1/k~f~ = (2π / βDωω~u~)) × exp(βΔG~f~*) [79] [78]

where k~f~ is the folding rate coefficient, D* is the diffusion coefficient at the barrier top, ω* and ω~u~ are the curvatures of the free energy surface at the barrier top and unfolded well, respectively, ΔG~f~* is the barrier height, β = 1/k~B~T, k~B~ is Boltzmann's constant, and T is absolute temperature [79].

In contrast, the average transition path time for a high parabolic barrier is:

t~TP~ = 1 / (βD(ω)^2^) × ln(2e^γ^βΔG*) [79] [78]

where γ (= 0.577...) is Euler's constant [79].

A crucial distinction emerges from these equations: while folding times depend exponentially on barrier height, transition path times depend only logarithmically on ΔG* [79] [78]. This makes transition path times relatively insensitive to barrier height compared to folding rates, and more directly reflective of the diffusive dynamics across the barrier.

Experimental Methodologies

Single-Molecule FRET Fundamentals

Förster resonance energy transfer (FRET) measures distance-dependent energy transfer between a donor fluorophore and an acceptor fluorophore [79] [81]. The FRET efficiency E depends on the inter-dye distance R as:

E = R~0~^6^ / (R~0~^6^ + R^6^) [81]

where R~0~ is the Förster radius at which energy transfer is 50% efficient [81]. For protein folding studies, donor and acceptor fluorophores are attached at specific positions, with the folded state typically exhibiting higher FRET efficiency due to closer proximity between labeling sites [79] [78].

In single-molecule FRET folding experiments, proteins are immobilized on a coated glass surface, and fluorescence trajectories are recorded under laser excitation [79] [78]. By working near the denaturation midpoint, molecules transition frequently between folded and unfolded states, enabling observation of multiple transitions in individual trajectories [78].

The Maximum Likelihood Method for Transition Path Times

The primary challenge in measuring transition path times is their brevity—typically in the microsecond range—which is shorter than the binning times used in conventional single-molecule trajectory analysis [79] [78]. To overcome this limitation, Chung et al. developed a maximum likelihood method that analyzes photon-by-photon trajectories without binning [79] [78].

The key innovation involves comparing two kinetic models:

• A two-state model (UF) with instantaneous transitions
• A three-state model (UIF) with a virtual intermediate state I representing the transition state ensemble

The lifetime τ~s~ of this virtual state corresponds to the average transition path time t~TP~ [78]. The analysis determines whether the likelihood ratio Δln L = ln L(τ~s~) - ln L(0) shows a statistically significant maximum at a particular τ~s~ value, indicating a finite transition path time [79] [78]. This approach can measure transition path times shorter than the photon arrival time by collectively analyzing many transitions [78].

Figure 1: Experimental workflow for measuring transition path times using single-molecule FRET. The key innovation is the maximum likelihood analysis of photon-by-photon data without binning.

Key Experimental Findings and Data

Transition Path Times for Different Proteins

Application of the maximum likelihood method to various proteins has revealed transition path times in the microsecond range, consistent with all-atom molecular dynamics simulations [79] [78]. Representative data include:

Table 1: Experimentally Determined Transition Path Times

Protein	Transition Path Time	Conditions	Folding Time	Reference
FBP28 WW domain	~2 μs	Aqueous buffer	~10-20 μs	[78]
FBP28 WW domain	~16 μs	50% glycerol (10 cP viscosity)	~100-200 μs	[78]
Protein GB1	< 10 μs (upper bound)	Aqueous buffer	~100 ms	[78]
35-residue WW domain	Finite t~TP~ detected	Not specified	Not specified	[79]
56-residue α/β protein	Finite t~TP~ detected	Not specified	Not specified	[79]

The viscosity dependence observed for FBP28 WW domain (10-fold slowing in 50% glycerol) confirms that transition path times are governed by diffusive dynamics, as predicted by Kramers-type theories [78].

Testing Theoretical Predictions

Transition path time measurements have provided critical tests of fundamental theoretical predictions:

• Barrier height insensitivity: The logarithmic dependence of t~TP~ on ΔG* was confirmed by comparing fast-folding (FBP28) and slow-folding (GB1) proteins. While their folding times differed by ~10^4^-fold, their transition path times differed by less than an order of magnitude [78].

• Validation of 1D diffusion model: The agreement between experimental t~TP~ values and all-atom MD simulations supports the validity of describing protein folding as diffusion on a one-dimensional free energy surface [79].

• Relationship to molecular timescales: The ~2 μs transition path time for FBP28 in water is consistent with the ~2 μs "molecular phase" observed in ensemble experiments on similar fast-folding proteins [78].

The Scientist's Toolkit: Essential Research Reagents

Table 2: Key Reagents and Materials for Single-Molecule FRET Transition Path Studies

Reagent/Material	Function/Application	Examples/Specifications
Fluorescent Dyes	Donor-acceptor FRET pair for distance measurement	Alexa Fluor 546/Alexa Fluor 647; specific labeling via maleimide chemistry [81]
Surface Coating	Immobilization while minimizing denaturation	Star-shaped polyethylene glycol (PEG) polymers; biotin-streptavidin linkage [81]
Denaturants	Modulating folding stability for midpoint studies	Guanidinium chloride (GdmCl); urea [81]
Viscogens	Modulating solvent viscosity to probe diffusive dynamics	Glycerol; sucrose solutions [78]
Microscopy Substrates	Single-molecule imaging	Coated glass coverslips; passivated surfaces [78] [81]
N2-iso-Butyroyl-5'-O-DMT-3'-deoxy-3'-fluoroguanosine	N2-iso-Butyroyl-5'-O-DMT-3'-deoxy-3'-fluoroguanosine, MF:C35H36FN5O7, MW:657.7 g/mol	Chemical Reagent
trans-5,6-Epoxy-9(Z),12(Z)-octadecadienoic acid	trans-5,6-Epoxy-9(Z),12(Z)-octadecadienoic acid, MF:C18H30O3, MW:294.4 g/mol	Chemical Reagent

Connection to Levinthal's Paradox and Molecular Dynamics

Transition path time measurements provide direct experimental insight into the resolution of Levinthal's paradox. The paradox asked how proteins could possibly search all possible conformations to find the native state in reasonable times [44] [41]. The observed transition path times of ~1-20 μs demonstrate that proteins do not sample the vast conformational space randomly but are guided by a biased energy landscape [78] [41].

Molecular dynamics simulations have been crucial in interpreting these results. All-atom simulations show that during folding, proteins sample only a tiny fraction (<400 clusters) of the possible unfolded conformations (>>15,000 clusters) [41]. This selective sampling is enabled by a downhill energy gradient that efficiently directs the chain toward the native state [41]. The agreement between experimental transition path times and MD simulations validates these computational models and their ability to capture the essential physics of protein folding [79].

Furthermore, Markov State Models (MSMs) built from MD simulations have enabled quantitative analysis of folding pathways and mechanisms [82] [83]. Transition path theory applied to MSMs allows computation of the flux network between states, revealing dominant folding pathways and the commitment probabilities (committors) of intermediate states [82].

Figure 2: The relationship between transition path measurements, Levinthal's paradox, and molecular dynamics simulations. Experimental transition path times provide a crucial link between theory and simulation.

The measurement of transition path times represents a significant advance in protein folding studies, providing direct access to the barrier-crossing events that contain the essential mechanistic information. Current efforts focus on extending these measurements to more complex systems, including multi-state proteins, membrane proteins, and protein-nucleic acid complexes [80].

Technological improvements continue to push the boundaries of what is possible:

• Improved time resolution through higher illumination intensities and brighter fluorophores
• Multi-color FRET for monitoring multiple distances simultaneously
• Combined techniques integrating fluorescence with force spectroscopy
• Advanced analysis methods for extracting structural information from transition paths

The ultimate goal is to obtain structural information during the transition path itself, allowing direct comparison with the structural predictions from all-atom MD simulations and analytical models [79] [80]. This would provide an unprecedented view of the protein folding process at atomic resolution.

In conclusion, single-molecule FRET measurements of transition path times have opened a new window into the protein folding process, providing stringent tests of theory and simulation, and advancing our understanding of how proteins navigate their energy landscape to achieve their functional native states. These advances represent a significant step toward resolving the fundamental questions raised by Levinthal's paradox nearly five decades ago.

Cross-Validation with NMR, HDX, and Cryo-EM for Excited States

The study of protein excited states—transient, low-populated conformational ensembles that are critical for function—represents a major frontier in structural biology. These states are central to processes such as enzyme catalysis, ligand binding, and allosteric regulation, yet they elude conventional structural determination methods due to their sparse populations and transient nature [84]. This challenge is fundamentally connected to Levinthal's paradox, which highlights the astronomical complexity of the protein conformational landscape while simultaneously questioning how proteins fold to their native states so rapidly [17] [4]. The existence of these excited states demonstrates that proteins do not exist as single static structures but rather as dynamic ensembles navigating a rugged energy landscape [84] [4].

Understanding these states requires a paradigm shift from the traditional focus on static structures to an ensemble perspective of interconverting conformers [84]. This whitepaper provides a comprehensive technical guide for investigating these elusive species through the integrated use of Nuclear Magnetic Resonance (NMR), Hydrogen-Deuterium Exchange Mass Spectrometry (HDX-MS), and Cryo-Electron Microscopy (Cryo-EM). By leveraging the complementary strengths of these techniques, researchers can achieve atomic-resolution insights into protein dynamics and excited states, thereby advancing fundamental understanding of protein function and facilitating drug discovery efforts.

Theoretical Framework: Energy Landscapes and the Biological Significance of Excited States

The Energy Landscape Theory

The conformational space available to a biomolecule is best described by the energy landscape theory, which governs the thermodynamics and kinetics of conformational transitions [84]. A protein's free energy landscape is typically rugged, featuring a global minimum corresponding to the native state and local minima representing low-lying excited states separated by free-energy barriers that can be overcome by thermal fluctuations [84]. The Principle of Maximum Entropy suggests that at physiological temperatures, proteins sample a ensemble of conformations with higher entropy than those captured at cryogenic temperatures [85].

Functional Roles of Excited States

Excited states, despite their low population (often ≤5%) and transient nature, play indispensable roles in biological function [84]:

• Protein folding and misfolding: Folding intermediates may nucleate aggregation processes implicated in disease [84]
• Molecular recognition and ligand binding: Excited states enable conformational selection mechanisms [84]
• Enzyme catalysis: Transient states often represent catalytic intermediates [86]
• Allosteric regulation: Excited states facilitate communication between distant sites [86]

Technical Guide to Investigating Excited States

Solution NMR Spectroscopy

NMR is uniquely powerful for characterizing biomolecular dynamics at atomic resolution across multiple timescales, with particular strength in the microsecond-to-millisecond (μs-ms) regime where many functionally relevant motions occur [86].

Key NMR Methods for Excited States

Table: NMR Methods for Characterizing Excited States

Method	Timescale (s⁻¹)	Population Limit	Structural Information	Key Applications
CPMG Relaxation Dispersion	200-2,000	≥1%	Chemical shifts (ϖE)	Protein folding, enzyme catalysis [84] [86]
CEST	20-300	≥1%	Chemical shifts (ϖE)	Molecular recognition, sparse states [84] [86]
R1ρ	Up to 40,000	≥1%	Chemical shifts, exchange rates	Fast conformational exchange [84]
PRE	Rapid exchange	≥0.5%	Long-range distances (up to 35Å)	Global structural features, transient interactions [84]

Experimental Protocol for CPMG Relaxation Dispersion

Principle: Measures the effective transverse relaxation rate (R_2,eff) as a function of the frequency of applied refocusing pulses (ν_CPMG) to characterize chemical exchange processes [84] [86].

Sample Requirements:

• Uniformly ¹⁵N- and/or ¹³C-labeled protein (≥200 μM in NMR buffer)
• Stable temperature control (±0.1°C)
• Deuterated buffer for lock signal

Data Collection:

• Set up a series of 2D ¹⁵N-HSQC spectra with varying CPMG field strengths (ν_CPMG)
• Typical ν_CPMG range: 50-1000 Hz
• Measure peak intensities (I) at each ν_CPMG point
• Calculate R_2,eff = -1/T * ln(I/I₀), where T is the total relaxation period
• Repeat for multiple temperatures to separate exchange contributions

Data Analysis:

• Fit R_2,eff vs. ν_CPMG profiles to appropriate exchange models (e.g., 2-state)
• Extract parameters: k_ex (exchange rate), p_E (excited state population), Δϖ_GE (chemical shift difference)
• Use chemical shifts of excited state (Ï–_E) with CS-Rosetta or similar algorithms to calculate structures [84]

Diagram Title: NMR CPMG Relaxation Dispersion Workflow

Hydrogen-Deuterium Exchange Mass Spectrometry (HDX-MS)

HDX-MS provides a powerful approach for mapping protein dynamics and excited states by measuring the exchange rate of amide protons with solvent deuterons, reporting on structural stability and conformational fluctuations [87].

HDX-MS Principles and Applications

Principle: Amide proton exchange occurs when a hydrogen-bonded proton becomes exposed to solvent through transient "open states" [87]. The denaturant dependence of HDX identifies the size of opening events:

• Local unfolding: Minimal denaturant dependence
• Subglobal unfolding: Moderate denaturant dependence
• Global unfolding: Strong denaturant dependence matching global stability [87]

Key Applications:

• Mapping free energy surfaces (FES) of proteins [87]
• Identifying rare states through their H-bond stability [87]
• Characterizing folding intermediates and misfolded states [87]

Experimental Protocol for HDX-MS

Sample Requirements:

• Purified protein (10-50 μM in appropriate buffer)
• Deuterated buffer (pDread = pHread + 0.4)
• Quench solution (low pH, low temperature)
• LC-MS system with pepsin column/protease XIII

Data Collection:

• Initiate Exchange: Dilute protein 10-15 fold into Dâ‚‚O buffer
• Incubate: Allow exchange for variable times (seconds to hours) at controlled temperature
• Quench: Lower pH to 2.5 and temperature to 0°C to minimize back-exchange
• Digest: Pass through immobilized protease column (≤3 minutes)
• Separate and Analyze: Use UPLC coupled to high-resolution mass spectrometer
• Denaturant Dependence: Repeat at multiple denaturant concentrations (0-4 M GdmCl)

Data Analysis:

• Identify peptides and measure deuterium incorporation
• Calculate protection factors: PF = k_int/k_obs, where k_int is intrinsic exchange rate
• Determine free energy of opening: ΔG_HX = -RT ln(k_obs/k_int)
• Classify opening events based on denaturant dependence (m-value)
• Map protection factors onto protein structure

Cryo-Electron Microscopy (Cryo-EM)

While traditionally used for determining high-resolution static structures, Cryo-EM can provide insights into conformational heterogeneity when combined with advanced computational approaches.

Addressing the Temperature Discrepancy

A critical consideration in Cryo-EM studies of dynamics is that rapid cooling during sample preparation may not preserve physiological conformations [85]. Molecular dynamics (MD) simulations at 310 K starting from Cryo-EM reconstructions can reveal conformations favored at physiological temperatures that differ from those observed in frozen samples [85].

Experimental Protocol for Cryo-EM of Dynamic Systems

Sample Requirements:

• Homogeneous protein/complex preparation (≥0.5 mg/mL)
• Optimized vitrification conditions (blotting time, humidity)
• High-quality grids (ultrafoil, graphene oxide)

Data Collection for Heterogeneity Analysis:

• Collect large datasets (≥1,000 micrographs) using modern detectors
• Use energy filter and small defocus range for high-resolution information
• Maximize particle numbers (≥100,000 particles)

Data Processing for Conformational Heterogeneity:

• Reference-free 2D Classification: Remove poorly centered particles
• Ab Initio Reconstruction: Generate initial models without bias
• Heterogeneous Refinement: Separate particles into multiple classes
• 3D Variability Analysis: Identify continuous conformational changes
• Focus Refinement: Improve resolution of specific regions

Integrative Cross-Validation Framework

Complementary Technical Strengths

Table: Cross-Validation of Biophysical Techniques for Excited States

Parameter	NMR	HDX-MS	Cryo-EM	MD Simulations
Timescale Sensitivity	ps-s (μs-ms optimal) [86]	ms-min (global) to s-h (local) [87]	Static snapshot	fs-μs (enhanced sampling extends this) [87]
Population Detection Limit	≥0.5% (PRE) to ≥1% (RD/CEST) [84]	≥1% (depends on ΔG) [87]	≥5-10% (heterogeneity analysis)	Boltzmann-weighted
Structural Resolution	Atomic (backbone) [84]	Peptide-level (5-15 residues) [87]	2-4Ã… (global), lower for flexible regions	Atomic (all atoms) [87]
Key Excited State Information	Atomic structure, kinetics, thermodynamics [84]	Stability, unfolding cooperativity, FES mapping [87]	Global conformations, large-scale movements [85]	Atomic pathways, energetics, water dynamics [87] [85]
Sample Requirements	¹⁵N/¹³C-labeled, 200μM-1mM, <70kDa [84]	Unlabeled, 10-50μM, no size limit [87]	≥0.5mg/mL, size ≥50kDa preferred	Atomic coordinates

Strategic Integration for Comprehensive Understanding

The most powerful insights emerge from strategic combination of these techniques:

Diagram Title: Multi-Technique Cross-Validation Strategy

Example Integration Workflow:

• Initial Characterization: Use HDX-MS to identify dynamic regions and estimate populations and stabilities of excited states [87]
• Atomic Details: Apply NMR relaxation dispersion to determine atomic-level structures and kinetics of identified excited states [84]
• Global Context: Employ Cryo-EM to visualize large-scale conformational changes and place NMR-identified states in structural context [85]
• Computational Integration: Utilize MD simulations to connect states, estimate free energies, and predict pathways [87] [85]

Research Reagent Solutions

Table: Essential Research Reagents for Excited State Studies

Reagent/Category	Specific Examples	Function & Application
Isotope Labeling	¹⁵N-NH₄Cl, ¹³C-glucose, D₂O	NMR: Enables detection of protein signals; HDX: Solvent for exchange [84]
Paramagnetic Probes	MTSL, EDTA-based metal chelators	NMR: PRE measurements for long-range distance restraints [84]
Proteases	Pepsin, Protease XIII, Nepenthesin-2	HDX-MS: Rapid digestion under quench conditions [87]
Denaturants	Guanidine HCl, Urea	HDX: Probing opening event size; MD: Force field validation [87]
Vitrification Reagents	Graphene oxide grids, UltraFoil holes	Cryo-EM: Improved particle distribution and ice quality [85]
Molecular Biology	Site-directed mutagenesis kits	All techniques: Creating conformational biases and functional probes
MD Software & Force Fields	Upside, CHARMM36, AMBER, GROMACS	Simulation: Generating and validating conformational ensembles [87]

Reconciliation with Levinthal's Paradox and Molecular Dynamics

The investigation of excited states through these integrated biophysical approaches provides a resolution to the apparent contradiction posed by Levinthal's paradox. Rather than randomly sampling all possible conformations, proteins navigate their energy landscapes through defined pathways involving stable intermediates and excited states [17] [4]. The funnel-shaped energy landscape theory, supported by experimental data from NMR, HDX, and Cryo-EM, explains how proteins can rapidly fold to their native states while still sampling functionally relevant excited conformations [4].

Molecular dynamics simulations, when cross-validated with experimental data, reveal how the ruggedness of the energy landscape creates local minima corresponding to excited states that facilitate biological function [87]. The combination of these approaches demonstrates that proteins exploit these landscapes efficiently, with excited states serving as stepping stones between major conformational states rather than as kinetic traps [84] [87].

The comprehensive cross-validation of NMR, HDX-MS, and Cryo-EM represents the state-of-the-art approach for characterizing protein excited states. By leveraging their complementary strengths—NMR for atomic-resolution dynamics, HDX-MS for stability and unfolding measurements, and Cryo-EM for global structural context—researchers can achieve unprecedented insights into the conformational ensembles that underlie protein function. This integrated methodology not only advances our fundamental understanding of protein dynamics but also provides critical information for drug discovery, where targeting excited states offers new therapeutic opportunities. As these techniques continue to evolve, their strategic integration will remain essential for unraveling the complexity of protein energy landscapes and their biological implications.

The problem of how a protein folds into its unique three-dimensional structure is a fundamental challenge in molecular biology, famously framed by Cyrus Levinthal's paradox [43] [14]. Levinthal calculated that a random, exhaustive search of all possible conformations would take an astronomical amount of time, longer than the age of the universe, for a protein to find its native state [14]. Yet, in reality, proteins fold on timescales ranging from microseconds to minutes [43]. This paradox highlighted that protein folding cannot be a random search but must be a directed process guided by a specific, energetically favorable pathway [36]. The solution to this paradox lies in the concept of a funneled energy landscape, where the protein's conformational space is biased toward the native state, steering the folding process through a series of intermediate states without requiring an exhaustive search [43] [44].

This theoretical framework underpins the two powerful computational approaches dominating the field today: Molecular Dynamics (MD) simulations and AI-based structure prediction. MD simulations attempt to model the physical folding process by calculating the forces and motions of atoms over time, directly addressing the "how" of folding [43]. In contrast, modern AI tools like AlphaFold2 and trRosetta leverage deep learning on vast databases of known protein structures to predict the final folded state from an amino acid sequence, primarily addressing the "what" of the structure [43] [36]. This review provides a comparative analysis of these methodologies, evaluating their principles, strengths, limitations, and protocols within the context of resolving Levinthal's paradox and advancing molecular dynamics research.

Theoretical Foundations and Computational Principles

Molecular Dynamics (MD) Simulations

MD simulation is a rigorous computational method based on classical Newtonian physics. It models the dynamic evolution of a molecular system by numerically solving Newton's equations of motion for every atom. The core of an MD simulation is the force field, a mathematical function that describes the potential energy of the system as a sum of bonded terms (bonds, angles, dihedrals) and non-bonded terms (van der Waals, electrostatic interactions). The accurate representation of these forces is crucial for simulating biologically relevant processes like protein folding, conformational changes, and ligand binding [88]. The "thermodynamic accuracy" of a simulation—its ability to reliably predict free energy differences (ΔG) between conformational states—is paramount because protein function often depends on rare transitions between these states [89].

While MD can, in principle, provide an atomistically detailed view of the folding pathway, it is computationally besieged by the "sampling problem." The timescales of functionally relevant conformational changes (microseconds to milliseconds) often exceed what is practical to simulate with conventional MD, even on supercomputers [89]. This limitation has driven the development of enhanced sampling methods and, more recently, the integration of machine learning to create faster, more efficient simulations.

AI-Based Protein Structure Prediction

AI-based prediction tools represent a paradigm shift, bypassing the physical folding process to directly predict the final, native structure. These methods can be broadly categorized as template-based modeling (TBM) and template-free modeling (TFM), though modern deep learning approaches blur this distinction [36].

• AlphaFold2: A groundbreaking deep learning system that uses an attention-based neural network architecture (Evoformer). [36] It processes multiple sequence alignments (MSAs) to generate accurate predictions of residue-residue distances and angles, which are then used to build an atomic model [36]. Its success is largely attributed to training on the vast structural information in the Protein Data Bank (PDB).
• trRosetta (transform-restrained Rosetta): This method employs a deep residual neural network to predict inter-residue geometries, including distances and orientations. These predicted geometries are then transformed into restraints to guide structure construction through direct energy minimization [88] [36].
• RoseTTAFold (within Robetta): A three-track deep neural network that simultaneously considers patterns in protein sequences, distances between amino acids, and their coordinates in three-dimensional space, enabling iterative refinement of a protein model [88].

A critical acknowledgement is that these AI tools, while often called "de novo," are indirectly dependent on known structural information as they are trained on large-scale PDB data. Their performance can thus be limited when predicting structures of proteins that lack homologous counterparts in the PDB, highlighting a continued role for true ab initio methods [36].

Comparative Analysis: Performance, Accuracy, and Limitations

A direct comparison of these methodologies reveals a complementary relationship, with each excelling in different areas. The following table summarizes the core characteristics of MD simulations versus AI-based prediction tools.

Table 1: Core Characteristics of MD Simulations vs. AI-Based Prediction Tools

Feature	Molecular Dynamics (MD)	AI-Predictions (e.g., AF2, trRosetta)
Fundamental Principle	Physics-based, Newtonian mechanics	Statistics-based, pattern recognition from databases
Primary Output	Time-evolving trajectory of atomic positions	Static, single or ensemble of 3D structures
Temporal Resolution	Femtosecond to millisecond (often limited)	Instantaneous prediction
Strength in Folding Context	Models the pathway and kinetics of folding	Predicts the final folded state
Treatment of Dynamics	Explicitly models full dynamics and flexibility	Limited inherent dynamics; newer tools (BioEmu) generate ensembles
Computational Cost	Extremely high (CPU/GPU-intensive)	Relatively low for a single prediction
Key Limitations	Sampling challenges, timescale gaps, force field inaccuracies	Dependence on training data, limited insight into folding pathways

Accuracy and Refinement Needs

While AI tools have achieved remarkable accuracy, predicted structures often require refinement to be suitable for downstream applications like drug docking. A study on modeling the Hepatitis C virus core protein (HCVcp) found that initial models from AF2, Robetta, and trRosetta showed variations, and subsequent MD simulations were crucial for refining these structures into compact, stable folds with improved quality scores [88]. The same study noted that in initial predictions, Robetta and trRosetta outperformed AF2 for this specific viral protein, while among template-based methods, a domain-based homology modeling approach using MOE outperformed I-TASSER [88] [90].

MD simulation serves as a powerful refinement tool because it can relax steric clashes and optimize side-chain and backbone packing in a physically realistic manner, driving the model toward a lower energy conformation that may not be captured in the initial AI prediction.

The Rise of Hybrid and Next-Generation AI Tools

The distinction between MD and AI is increasingly blurring with the advent of new hybrid technologies. A prime example is BioEmu, a generative AI system that aims to emulate protein equilibrium ensembles [89]. BioEmu combines AlphaFold2's sequence understanding with a diffusion model to generate not just one structure, but a diverse ensemble of structures representing the protein's dynamic states. It achieves a 4–5 orders of magnitude speedup for estimating equilibrium distributions compared to traditional MD, running on a single GPU instead of requiring supercomputers for months [89].

This approach demonstrates exceptional thermodynamic accuracy (within 1 kcal/mol) by being fine-tuned on massive MD datasets and experimental stability measurements [89]. It can sample large-scale conformational changes, such as open-closed transitions, and reveal "cryptic pockets" for drug targeting—tasks that were previously infeasible with standard MD or static AI predictions.

Experimental Protocols and Methodologies

Protocol for AI-Driven Structure Prediction and Refinement

The following workflow outlines a standard protocol for predicting a protein structure using AI tools and refining it with MD simulations, as demonstrated in studies of viral proteins [88].

Diagram 1: AI Prediction and MD Refinement Workflow (Title: Protein Modeling Workflow)

Step 1: Secondary Structure Prediction. Initiate with a tool like PSIPRED to analyze the amino acid sequence and predict regions of alpha-helices, beta-sheets, and coils [88]. This provides an initial structural blueprint.

Step 2: 3D Structure Prediction. Run the sequence through multiple AI prediction tools.

• De Novo AI Tools (AF2, Robetta, trRosetta): Submit the sequence to the respective web servers. These tools do not require a structural template and generate models based on deep learning. For example, using the RoseTTAFold algorithm in Robetta provides models with continuous automated evaluation [88].
• Template-Based Tools (I-TASSER, MOE): I-TASSER automatically identifies templates. For MOE, if a full-length template is unavailable, perform domain-based homology modeling. Identify templates for individual domains via NCBI BLAST against the PDB, then model and assemble domains into a full-length structure [88].

Step 3: Initial Model Comparison and Quality Assessment. Compare the generated models visually and quantitatively. Calculate quality scores to select the most promising initial model for refinement.

Step 4: MD Simulation Refinement. Subject the chosen model to an MD simulation in explicit solvent. A typical protocol involves:

• Energy minimization to remove steric clashes.
• Solvation in a water box and addition of ions to neutralize the system.
• Equilibration of the solvent and ions around the protein with positional restraints on the protein atoms.
• Production run without restraints. Monitor convergence by calculating metrics like the Root Mean Square Deviation (RMSD) of the protein backbone and the Radius of Gyration (Rg) over time [88].

Step 5: Final Quality Validation. After the simulation has stabilized (reached a plateau in RMSD), extract representative structures and validate them using tools like ERRAT (for overall statistics) and phi-psi (Ramachandran) plots (for stereochemical quality) [88].

Protocol for Training a Generative AI Model like BioEmu

The development of next-generation tools like BioEmu follows a sophisticated, multi-stage training process [89].

Diagram 2: Generative AI Training Pipeline (Title: Generative AI Training Stages)

Stage 1: Pretraining. The model (e.g., using AlphaFold2's Evoformer module) is first trained on a processed version of the AlphaFold database. This stage establishes a foundational understanding of how sequences map to structures. Data augmentation is critical here to prevent overfitting to static structures and to teach the model about conformational diversity [89].

Stage 2: Training on MD Data. The model is further trained on thousands of protein MD simulation datasets, totaling hundreds of milliseconds of simulation time. These trajectories are reweighted using Markov State Models (MSMs) to represent equilibrium distributions, teaching the model the relative probabilities of different conformational states [89].

Stage 3: Property Prediction Fine-Tuning (PPFT). This innovative stage fine-tunes the model on hundreds of thousands of experimental measurements (e.g., melting temperature Tm, free energy changes ΔΔG). The PPFT algorithm performs a joint optimization, ensuring the generated ensemble's properties match the experimental data, thereby building direct thermodynamic accuracy into the model [89].

Table 2: Key Computational Tools and Databases for Protein Structure Research

Tool / Resource	Type	Primary Function	URL / Reference
AlphaFold2	AI Prediction Server	De novo protein structure prediction	https://colab.research.google.com/github/deepmind/alphafold/ [88]
Robetta Server	AI Prediction Server	De novo protein structure prediction (RoseTTAFold)	https://robetta.bakerlab.org/ [88]
trRosetta Server	AI Prediction Server	Predicts distances/orientations for structure building	https://yanglab.nankai.edu.cn/trRosetta/ [88]
I-TASSER	Template-Based Modeling	Automated protein structure and function prediction	[88]
MOE (Molecular Operating Environment)	Software Suite	Homology modeling, molecular modeling, and simulation	[88]
GROMACS / AMBER	MD Simulation Engine	Run molecular dynamics simulations	[88] [89]
Open Molecules 2025 (OMol25)	Training Dataset	>100M molecular snapshots for MLIP training	[91]
Protein Data Bank (PDB)	Database	Repository for experimentally-determined structures	[43] [36]
PSIPRED	Analysis Tool	Protein secondary structure prediction	http://bioinf.cs.ucl.ac.uk/psipred/ [88]

The comparative analysis of MD simulations and AI-based predictions reveals a rapidly evolving landscape where integration, not competition, is the path forward. MD simulations provide the physical basis and temporal dimension for understanding protein folding, directly addressing the mechanistic question posed by Levinthal's paradox. AI predictions, on the other hand, have spectacularly solved the problem of rapidly determining the native state from sequence, achieving accuracies that rival experimental methods in many cases.

The future lies in hybrid approaches that leverage the strengths of both paradigms. Technologies like BioEmu exemplify this trend by using generative AI trained on both MD data and experimental results to achieve scalable, thermodynamically accurate simulations of protein dynamics [89]. Furthermore, the emphasis on ethical data sharing and reproducible science will be crucial for generating the high-quality, diverse datasets needed to train the next generation of models, particularly for underrepresented protein classes and multi-chain complexes [92].

For researchers in drug development, this convergence means that tools for predicting not just static structures but dynamic ensembles and cryptic pockets are becoming accessible. This will profoundly impact target identification and ligand discovery, moving computational biology from a focus on single structures to a more holistic, physics-informed understanding of protein dynamics and function. The solution to Levinthal's paradox, therefore, has not only guided decades of research but continues to inspire the development of computational methods that are finally unlocking the full complexity of protein dynamics.

The rise of highly accurate protein structure prediction tools has fundamentally transformed structural biology. However, a critical question remains: can these static, predicted models adequately explain dynamic functional processes like allostery and catalysis? This whitepaper examines this question through the lens of Levinthal's paradox and molecular dynamics research. We evaluate the capabilities and limitations of current computational methods in capturing the complex conformational landscapes and dynamic motions essential for protein function. While coevolutionary analysis and machine learning show promise in identifying functional residues, molecular dynamics simulations remain indispensable for probing the temporal dimension of allosteric signaling and catalytic mechanisms. The integration of these complementary approaches provides the most robust framework for bridging the gap between predicted structures and biological function, with significant implications for drug development and protein engineering.

The Levinthal paradox highlights the fundamental challenge of protein folding, noting that proteins cannot possibly sample all possible conformations to reach their native state, suggesting the existence of guided folding pathways [17]. This paradox extends to structure prediction: while we can now predict static structures with remarkable accuracy, understanding how these structures facilitate dynamic processes like allostery and catalysis remains challenging.

Christian Anfinsen's thermodynamic hypothesis posited that a protein's native structure represents the thermodynamically most stable state under physiological conditions, determined solely by its amino acid sequence [4]. This principle underpins modern structure prediction algorithms. However, the analytical determination of protein 3D structure inevitably requires disrupting the thermodynamic environment, meaning that structures determined in vitro may not fully represent the active, functional conformations in their physiological milieu [17]. This creates a quantum mechanics-like paradox where the act of measurement may alter the very property being measured.

Allostery, "the second secret of life" alongside the genetic code, represents a particular challenge for predicted structures. It commonly refers to distant regulation where a perturbation at one site affects function at another site [93] [94]. This regulation occurs through complex dynamic processes that static structures may not fully capture. Similarly, enzyme catalysis often depends on precisely coordinated motions and transition state stabilizations that extend beyond what can be inferred from a single ground-state structure [94].

Theoretical Framework: From Static Structures to Dynamic Function

Energy Landscapes and Protein Dynamics

The energy landscape theory frames protein folding as a funnel-guided process where native states occupy energy minima [4]. The ruggedness of this landscape accounts for the heterogeneity and complexity observed in folding pathways and functional motions. This theoretical framework is crucial for understanding how predicted structures relate to function:

• Conformational ensembles: Functional proteins exist as ensembles of conformations rather than single structures
• Hierarchical timescales: Protein motions occur across multiple timescales, from sidechain rotations to domain movements
• Allosteric communication: Signal transmission can occur through specific pathways or through distributed changes in dynamics

Models of Allosteric Signaling

Two principal models describe allosteric signal transduction, each with implications for structure-based prediction:

Domino Model: A sequential set of events propagates linearly from the allosteric to the active site through specific structural pathways. This mechanism has been suggested for PDZ domains, GPCRs, and hemoglobin [95].

Violin Model: Binding of an effector changes the protein's vibrational patterns throughout the entire structure, with no single pathway for signal transduction. This model relies on changes in dynamic properties without significant conformational changes [95].

Table 1: Comparison of Allosteric Signaling Models

Feature	Domino Model	Violin Model
Signal Transmission	Sequential through specific pathways	Distributed throughout structure
Structural Changes	Significant conformational changes	Minimal conformational changes
Role of Dynamics	Facilitates sequential movements	Essential for signal propagation
Predictability from Static Structures	Moderate	Low

Computational Approaches for Functional Assessment

Coevolution-Based Methods

Coevolutionary coupling analysis provides a powerful approach to identify functionally important residues from sequence information alone. The KeyAlloSite method leverages evolutionary coupling models to predict allosteric sites and identify key allosteric residues [93].

Experimental Protocol: Coevolution Analysis

• Multiple Sequence Alignment (MSA)

  • Collect homologous sequences from databases
  • Perform alignment using tools like HHblits or JackHMMER
  • Filter sequences to reduce redundancy

• Evolutionary Coupling Calculation

  • Apply Direct Coupling Analysis (DCA) to remove indirect correlations
  • Compute evolutionary coupling scores between residue pairs
  • Focus on both strong and weak coupling terms, as weak couplings contain important allosteric information

• Allosteric Site Prediction

  • Calculate evolutionary coupling strength between orthosteric and potential allosteric pockets
  • Compare with coupling to non-functional sites
  • Identify residues with significant coupling differences as key allosteric residues

• Validation

  • Compare predictions with experimental data from mutagenesis studies
  • Test on well-characterized systems like BCR-ABL1, Tar, and PDZ3 domains

This approach has demonstrated that protein allosteric sites show stronger evolutionary coupling to orthosteric sites compared to non-functional sites, with 23 of 25 tested allosteric pockets showing Z-scores greater than 0.5 [93].

Molecular Dynamics-Based Approaches

Molecular dynamics simulations provide a complementary approach that directly captures the temporal dimension of protein function. The Molecular Dynamics-Based Allosteric Prediction (MBAP) method exemplifies this approach [96].

Experimental Protocol: MD-Based Allosteric Prediction

• System Preparation

  • Obtain initial structure from crystallography or prediction
  • Model missing residues or loops if necessary
  • Add missing hydrogen atoms
  • Perform molecular docking if complex structures unavailable

• Molecular Dynamics Simulation

  • Solvate the protein in explicit water molecules
  • Add counterions to neutralize system charge
  • Energy minimization and system equilibration
  • Production run (typically 100+ nanoseconds)
  • Analyze root mean square deviation to ensure system stability

• Binding Energy Decomposition

  • Use MM-GBSA method to calculate binding free energies
  • Decompose energy contributions to individual residues
  • Identify residues contributing significantly to binding

• Computer-Aided Mutagenesis

  • Perform in silico saturation mutagenesis of candidate residues
  • Run shorter MD simulations for each mutant
  • Calculate binding energy changes compared to wild-type
  • Select mutants with significant energy changes for experimental validation

This method successfully identified mutation P441L in threonine dehydrogenase, which significantly reduced allosteric regulation in both in vitro assays and fermentation applications [96].

Machine Learning and Graph Neural Networks

Recent advances in machine learning, particularly graph neural networks, show promise for predicting functional residues from structural information.

Experimental Protocol: Equivariant Graph Neural Networks

• Graph Representation

  • Represent protein structure as a graph with atoms as nodes
  • Define edges based on atomic connectivity or distance
  • Include node features (atomic numbers, residue types)
  • Add edge features (bond types, distances)

• Model Architecture

  • Implement equivariant graph neural network layers
  • Use message passing to update node representations
  • Apply attention mechanisms to weight important interactions
  • Include rotational and translational equivariance

• Training and Validation

  • Train on datasets of known functional residues
  • Use cross-validation to assess performance
  • Test on independent benchmark datasets
  • Compare with traditional methods

This approach has achieved mean absolute errors below 0.09 eV for predicting binding energies of intermediates at metallic interfaces, demonstrating robust performance across diverse catalytic systems [97].

Comparative Analysis of Methods

Table 2: Quantitative Comparison of Functional Assessment Methods

Method	Data Requirements	Key Metrics	Strengths	Limitations
KeyAlloSite (Coevolution)	Multiple sequence alignments	Z-score > 0.5 for allosteric sites	Identifies evolutionarily conserved allosteric networks	Requires large protein families; limited for novel folds
MBAP (MD Simulations)	Atomic-level structure	Binding energy decomposition (e.g., -18.29 ± 3.95 kcal/mol for wild-type TD)	Captures temporal dynamics; provides energetic insights	Computationally intensive; limited timescales
Squidly (Machine Learning)	Protein sequences	F1 score: 0.85 (high homology), 0.64 (<30% identity)	Fast prediction; no structure required	Limited interpretability; dataset biases
Equivariant GNN	Atomic structure	MAE < 0.09 eV for binding energies	Handles complex adsorption motifs	Requires high-quality structures; complex implementation

Research Reagent Solutions

Table 3: Essential Research Reagents and Computational Tools

Reagent/Tool	Function	Application Examples
GROMACS	Molecular dynamics simulation package	Simulating allosteric transitions; calculating binding energies
AlphaFold2	Protein structure prediction	Generating initial structures for functional analysis
MM-GBSA	Binding free energy calculation	Decomposing energy contributions to individual residues
DCA Tools	Direct coupling analysis	Identifying coevolutionary networks from sequence data
PyMOL	Molecular visualization	Analyzing structural features and residue interactions
FoldSeek	Structural similarity search	Assessing structural conservation across homologs

Signaling Pathways and Workflows

Coevolution-Based Allosteric Residue Prediction

Molecular Dynamics Allosteric Prediction

Allosteric Signaling Mechanisms

Discussion and Future Perspectives

The integration of multiple computational approaches provides the most promising path forward for assessing functional relevance from predicted structures. Coevolution analysis captures evolutionary constraints on function, molecular dynamics simulations provide temporal resolution of functional motions, and machine learning methods enable rapid prediction across large datasets.

Protein kinases exemplify the importance of dynamics in function. Their internal architecture is built around dynamically assembled hydrophobic spines that connect the N-lobe and C-lobe [95]. The regulatory spine assembles in active kinases and disassembles in inactive states, while the catalytic spine is completed by ATP binding. These structural features facilitate the allosteric regulation essential for kinase function, yet they may not be fully apparent in single static structures.

For drug development professionals, these insights are crucial. Allosteric drugs offer advantages including higher specificity and fewer side effects compared to orthosteric drugs [93]. However, optimizing allosteric compounds faces challenges due to flat structure-activity relationships, where small modifications may destroy activity [93]. Understanding the dynamic nature of allosteric sites and identifying key allosteric residues through methods like KeyAlloSite can guide rational drug design.

Future research should focus on integrating temporal dimensions into structure-based predictions, developing multi-scale approaches that combine sequence-based, structure-based, and dynamics-based methods, and creating specialized databases linking predicted structures with functional annotations. As we continue to navigate the landscape of protein folding and proteostasis [4], the synergy between advanced prediction algorithms and functional validation will be essential for unlocking the full potential of structural biology in explaining biological function.

Conclusion

The synergy between molecular dynamics simulations, energy landscape theory, and artificial intelligence has effectively resolved Levinthal's paradox, revealing that proteins fold via guided diffusion on a funneled energy landscape rather than a random search. This paradigm shift has provided a robust physical framework for understanding protein folding. The convergence of computational predictions with experimental data from techniques like single-molecule FRET and NMR validates these models and builds confidence in their application. Looking forward, the integration of these powerful computational methods holds immense promise for biomedical research. It enables the rational drug design targeting specific conformational states, including cryptic and allosteric pockets, and offers new avenues for understanding and treating misfolding diseases. The future lies in developing multi-scale models that seamlessly integrate quantum effects, full cellular context, and accurate kinetics to fully capture the complexity of protein dynamics in health and disease.

References

• 1. towards solving the protein-folding problem computationally [https://pmc.ncbi.nlm.nih.gov/articles/PMC6790072/]
• 2. Levinthal's paradox - Wikipedia [https://en.wikipedia.org/wiki/Levinthal's_paradox]
• 3. Solution of Levinthal’s Paradox and a Physical Theory of Protein Folding Times - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC7072185/]
• 4. Navigating the landscape of protein folding and proteostasis [https://pmc.ncbi.nlm.nih.gov/articles/PMC12550075/]
• 5. Review Methods for exploring early events in protein folding [https://www.sciencedirect.com/science/article/abs/pii/S0959440X99000159]
• 6. Mega-scale experimental analysis of protein folding ... [https://www.nature.com/articles/s41586-023-06328-6]
• 7. Computational prediction of protein folding rate using ... [https://www.sciencedirect.com/science/article/pii/S0010482522011441]
• 8. Editorial: Understanding Protein Dynamics, Binding and ... [https://www.frontiersin.org/journals/molecular-biosciences/articles/10.3389/fmolb.2021.681364/full]
• 9. Dynamic Allostery: Evolution's Double-Edged Sword in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12341636/]
• 10. Protein dynamics underlying allosteric regulation [https://www.sciencedirect.com/science/article/pii/S0959440X23002427]
• 11. Anfinsen's dogma [https://en.wikipedia.org/wiki/Anfinsen%27s_dogma]
• 12. Into the fold - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC1456894/]
• 13. Anfinsen's dogma [https://www.wikidoc.org/index.php/Anfinsen%27s_dogma]
• 14. Levinthal's paradox [https://en.wikipedia.org/wiki/Levinthal%27s_paradox]
• 15. New class of protein misfolding simulated in high definition [https://science.psu.edu/news/Obrien8-2025]
• 16. Non-native entanglement protein misfolding observed in all ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12333692/]
• 17. Quantum mechanics paradox in protein structure prediction [https://www.sciencedirect.com/science/article/pii/S2950363925000109]
• 18. Folding funnel [https://en.wikipedia.org/wiki/Folding_funnel]
• 19. Single-molecule magnetic tweezers to unravel protein ... [https://link.springer.com/article/10.1007/s12551-025-01274-1]
• 20. Methods for molecular dynamics simulations of protein ... [https://www.sciencedirect.com/science/article/pii/S1046202304000568]
• 21. Molecular Dynamics Simulation of Protein Folding by ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC1303567/]
• 22. Accurate predictions of protein mutational effects ... [https://www.nature.com/articles/s42004-025-01771-0]
• 23. SimpleFold: Folding Proteins is Simpler than You Think [https://arxiv.org/abs/2509.18480]
• 24. Folding and binding cascades: Shifts in energy landscapes [https://pmc.ncbi.nlm.nih.gov/articles/PMC33715/]
• 25. Autotransporters: The Cellular Reshapes a Environment ... Folding [https://pmc.ncbi.nlm.nih.gov/articles/PMC3654826/]
• 26. Comparing Protein Folding In vitro and In vivo - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC3984617/]
• 27. Protein aggregation in vitro and in vivo: a quantitative ... [https://pubmed.ncbi.nlm.nih.gov/1367356/]
• 28. influence Cellular | IDEALS on protein folding [https://www.ideals.illinois.edu/items/89548]
• 29. Navigating protein landscapes with a machine-learned ... [https://www.nature.com/articles/s41557-025-01874-0]
• 30. Levinthal's paradox - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC48166/]
• 31. Toward predictive models of RNA cellular function [https://www.sciencedirect.com/science/article/pii/S0959440X24001428]
• 32. Molecular dynamics [https://en.wikipedia.org/wiki/Molecular_dynamics]
• 33. Molecular dynamics simulation for all - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC6209097/]
• 34. Force field (chemistry) [https://en.wikipedia.org/wiki/Force_field_(chemistry)]
• 35. Force Fields and Interactions - GitHub Pages [https://computecanada.github.io/molmodsim-md-theory-lesson-novice/01-Force_Fields_and_Interactions/index.html]
• 36. Protein structure prediction via deep learning: an in-depth ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12003282/]
• 37. Critical assessment of AI-based protein structure prediction [https://www.sciencedirect.com/science/article/pii/S2950363925000353]
• 38. Force Fields in Molecular Dynamics [https://www.compchems.com/force-fields-in-molecular-dynamics/]
• 39. Transition-path velocity as an experimental measure of barrier ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5976497/]
• 40. From byte to bench to bedside: molecular dynamics ... [https://bmcbiol.biomedcentral.com/articles/10.1186/s12915-023-01791-z]
• 41. Fast protein folding on downhill energy landscape - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC2323966/]
• 42. Nonequilibrium statistics of barrier crossings with ... [https://arxiv.org/html/2509.24533v1]
• 43. Protein folding problem: enigma, paradox, solution - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC9842845/]
• 44. The Levinthal paradox: yesterday and today [https://www.sciencedirect.com/science/article/pii/S1359027897000679]
• 45. Highly accurate protein structure prediction with AlphaFold [https://www.nature.com/articles/s41586-021-03819-2]
• 46. Overview of AlphaFold2 and breakthroughs in overcoming ... [https://www.sciencedirect.com/science/article/abs/pii/S0010482524007054]
• 47. AlphaFold2: A high-level overview | AlphaFold [https://www.ebi.ac.uk/training/online/courses/alphafold/inputs-and-outputs/a-high-level-overview/]
• 48. AlphaFold2 knows some protein folding principles - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC11383045/]
• 49. Transformative Role of Artificial Intelligence in Drug ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12406033/]
• 50. The Arch from the Stones: Understanding Protein Folding ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12451740/]
• 51. Beyond static structures: protein dynamic conformations ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12262120/]
• 52. Conformational ensembles for protein structure prediction [https://www.nature.com/articles/s41598-024-84066-z]
• 53. A comprehensive application of FiveFold for conformation ... [https://www.nature.com/articles/s41598-025-17022-0]
• 54. A comprehensive application of FiveFold for conformation ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12480659/]
• 55. Quantum Computing with a Cause: Understanding Protein ... [https://www.linkedin.com/pulse/quantum-computing-cause-understanding-protein-folding-rajib-rana-lusuc]
• 56. Advanced methods for accessing protein shape-shifting ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6422738/]
• 57. Enhanced Sampling Techniques in Molecular Dynamics ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4339458/]
• 58. Exploring the Levinthal limit in protein folding - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC5323343/]
• 59. PySAGES: flexible, advanced sampling methods ... [https://www.nature.com/articles/s41524-023-01189-z]
• 60. Machine learning driven advances in molecular dynamics ... [https://chemrxiv.org/engage/chemrxiv/article-details/67c941a3fa469535b9277f64]
• 61. Text has enhanced contrast | ACT Rule | WAI [https://www.w3.org/WAI/standards-guidelines/act/rules/09o5cg/]
• 62. Accurate machine learning force fields via experimental ... [https://www.nature.com/articles/s41524-024-01251-4]
• 63. From Wafer‑Scale Protein Simulations to Hybrid Quantum ... [https://beit.tech/blog/from-wafer-scale-protein-simulations-to-hybrid-quantum-chemistry-beit-s-latest-breakthroughs]
• 64. Anton (computer) [https://en.wikipedia.org/wiki/Anton_(computer)]
• 65. The Bespoke Supercomputing Architecture That Stood ... [https://www.nextplatform.com/2023/12/04/the-bespoke-supercomputing-architecture-that-stood-test-of-time/]
• 66. Anton 3 | PSC [https://www.psc.edu/resources/anton/]
• 67. Best CPU, GPU, RAM for Molecular Dynamics in 2024 ... [https://bizon-tech.com/blog/best-cpu-gpu-ram-for-molecular-dynamics?srsltid=AfmBOoo-9Cx2yqvLESidrLlFlYNGO4ltFkbyWS28_cNIDbUw2Nr5Wk91]
• 68. Enabling Scalable AI-Driven Molecular Dynamics ... [https://developer.nvidia.com/blog/enabling-scalable-ai-driven-molecular-dynamics-simulations/]
• 69. Study Suggests Today's Quantum Computers Could Aid ... [https://thequantuminsider.com/2025/07/15/study-suggests-todays-quantum-computers-could-aid-molecular-simulation/]
• 70. 从头算分子动力学AIMD与经典分子动力学MD的计算成本与 ... [https://www.huasuankeji.com/news/?p=333280]
• 71. 高毅勤团队发表GRASP：整合多源实验信息实现复合物建模 ... [https://www.chem.pku.edu.cn/tpxw/170078.htm]
• 72. Machine learning in molecular simulations of biomolecules [https://wulixb.iphy.ac.cn/en/article/doi/10.7498/aps.72.20231624]
• 73. GROMACS在鲲鹏920平台的性能分析及运行优化 [http://www.jfdc.cnic.cn/CN/10.11871/jfdc.issn.2096-742X.2024.04.016]
• 74. 如何使用NVIDIA Dynamo 减少KV 缓存瓶颈 [https://developer.nvidia.cn/blog/how-to-reduce-kv-cache-bottlenecks-with-nvidia-dynamo/]
• 75. 建模和模拟服务 - Certara [https://www.certara.com.cn/services/modeling-and-simulation-services/]
• 76. 通过战略性PBPK 建模优化药物开发 [https://www.labcorp.com/content/labcorp/zh/ch/biopharma/nonclinical/disciplines/metabolism/modeling/pbpk.html]
• 77. å°†AI与定量系统药理学相结合，革新药物发现 [https://hub.baai.ac.cn/view/48376]
• 78. Transition path times measured by single-molecule ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5702281/]
• 79. Protein Folding Transition Path Times from Single ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5826754/]
• 80. Transition Path Times Measured by Single-Molecule ... [https://www.sciencedirect.com/science/article/abs/pii/S0022283617302474]
• 81. Single-molecule FRET Study of Denaturant Induced ... [https://www.sciencedirect.com/science/article/abs/pii/S0022283605016372]
• 82. Transition Pathways - theory - Markov model [http://docs.markovmodel.org/lecture_tpt.html]
• 83. Everything you wanted to know about Markov State Models ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2933958/]
• 84. NMR paves the way for atomic level descriptions of sparsely ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3740838/]
• 85. Reaching the full potential of cryo-EM reconstructions with ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12363784/]
• 86. NMR methods for investigating functionally relevant ... [https://www.sciencedirect.com/science/article/pii/S2772516225000208]
• 87. Prediction and Validation of a Protein's Free Energy Surface ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8757463/]
• 88. Comparison, Analysis, and Molecular Dynamics ... [https://www.mdpi.com/2306-5354/10/9/1004]
• 89. BioEmu: AI‐Powered Revolution in Scalable Protein ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12643044/]
• 90. Comparison, Analysis, and Molecular Dynamics ... [https://tcu.elsevierpure.com/en/publications/comparison-analysis-and-molecular-dynamics-simulations-of-structu/]
• 91. A Record-Breaking Dataset to Train AI Models has Launched [https://newscenter.lbl.gov/2025/05/14/computational-chemistry-unlocked-a-record-breaking-dataset-to-train-ai-models-has-launched/]
• 92. While AI Could Be the Game Changer in Predicting Health ... [https://www.medschool.umaryland.edu/news/2025/while-ai-could-be-the-game-changer-in-predicting-health-outcomes-it-should-not-be-the-only-method.html]
• 93. Coevolution-based prediction of key allosteric residues for protein function regulation | eLife [https://elifesciences.org/articles/81850]
• 94. Allosteric regulation and catalysis emerge via a common route | Nature Chemical Biology [https://www.nature.com/articles/nchembio.98]
• 95. Dynamics driven allostery in protein kinases - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC4630092/]
• 96. Molecular Dynamics-Based Allosteric Prediction Method to ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC8153896/]
• 97. Resolving chemical-motif similarity with enhanced atomic ... [https://www.nature.com/articles/s41467-025-63860-x]