Calculating Diffusion Coefficients with ReaxFF MD: A Comprehensive Tutorial from Fundamentals to Advanced Applications

Samantha Morgan Dec 02, 2025 196

This tutorial provides a comprehensive guide for researchers and scientists on calculating diffusion coefficients using ReaxFF molecular dynamics.

Calculating Diffusion Coefficients with ReaxFF MD: A Comprehensive Tutorial from Fundamentals to Advanced Applications

Abstract

This tutorial provides a comprehensive guide for researchers and scientists on calculating diffusion coefficients using ReaxFF molecular dynamics. Covering foundational concepts, step-by-step methodologies, troubleshooting of common issues, and validation techniques, this resource bridges theoretical knowledge with practical application. Using a Li-ion battery cathode material as a primary case study, we demonstrate the complete workflow from system preparation and simulated annealing to Mean Squared Displacement and Velocity Autocorrelation Function analysis. The content also addresses critical aspects like finite-size effects, parameterization challenges, and temperature extrapolation via the Arrhenius equation, equipping computational researchers with the essential skills to accurately simulate mass transport in complex reactive systems.

Understanding ReaxFF Fundamentals and Diffusion Theory for Reactive Systems

ReaxFF is a powerful computational engine for modeling chemical reactions with atomistic potentials based on the reactive force field approach. It represents a significant advancement in molecular simulation by bridging the gap between quantum mechanical accuracy and classical computational efficiency. Developed by Prof. Adri van Duin and coworkers, ReaxFF has been modernized, parallelized, and greatly optimized by SCM, making it suitable for large-scale simulations of complex reactive systems [1].

Unlike traditional force fields that require predefined connectivity between atoms—thus precluding simulations of reactive events—ReaxFF employs a bond-order formalism where bond order is empirically calculated from interatomic distances. This approach allows for continuous bond formation and breaking during simulations, enabling the study of chemical reactions without the prohibitive computational cost of quantum mechanical methods [2] [3]. The force field describes reactive events through a bond-order formalism, treating electronic interactions driving chemical bonding implicitly, which allows the method to simulate reaction chemistry without explicit QM consideration [2].

The ReaxFF potential energy is calculated as a sum of various contributions [2]:

[E{\text{system}} = E{\text{bond}} + E{\text{over}} + E{\text{angle}} + E{\text{tors}} + E{\text{vdWaals}} + E{\text{Coulomb}} + E{\text{Specific}}]

This comprehensive energy description enables ReaxFF to accurately model both covalent and electrostatic interactions for a diverse range of materials, making it particularly valuable for studying complex processes in materials science, catalysis, and energy storage systems.

Theoretical Framework and Methodology

Bond-Order Formalism

The foundational concept of ReaxFF is its bond-order formalism, which enables the dynamic formation and breaking of chemical bonds during simulations. The bond order between atoms i and j is calculated directly from interatomic distance using the empirical formula [2]:

[ BO{ij} = BO{ij}^\sigma + BO{ij}^\pi + BO{ij}^{\pi\pi} = \exp\left[p{bo1}\left(\frac{r{ij}}{ro^\sigma}\right)^{p{bo2}}\right] + \exp\left[p{bo3}\left(\frac{r{ij}}{ro^\pi}\right)^{p{bo4}}\right] + \exp\left[p{bo5}\left(\frac{r{ij}}{ro^{\pi\pi}}\right)^{p{bo6}}\right] ]

Where BO is the bond order between atoms i and j, rij is interatomic distance, ro terms are equilibrium bond lengths, and p_bo terms are empirical parameters. This equation is continuous, containing no discontinuities through transitions between σ, π, and ππ bond character, which yields a differentiable potential energy surface required for the calculation of interatomic forces [2].

Energy Contributions

ReaxFF incorporates multiple energy contributions to accurately describe molecular interactions:

  • Bond Energy (E_bond): A continuous function of interatomic distance that describes the energy associated with forming bonds between atoms.
  • Overcoordination Penalty (E_over): Prevents over-coordination of atoms based on atomic valence rules.
  • Angle Strain (E_angle): Energy associated with three-body valence angle strain.
  • Torsional Strain (E_tors): Energy associated with four-body torsional angle strain.
  • Non-bonded Interactions (EvdWaals and ECoulomb): Electrostatic and dispersive contributions calculated between all atoms, regardless of connectivity.
  • System Specific Terms (E_Specific): Additional terms for specific systems, such as lone-pair, conjugation, hydrogen binding, and C2 corrections [2].

Force Field Parameterization

ReaxFF requires extensive parameterization to cover the relevant chemical phase space. Parameters are typically trained against quantum mechanical data, often using density functional theory (DFT) calculations. The complexity of the ReaxFF functional form necessitates comprehensive training sets covering bond and angle stretches, activation and reaction energies, equation of state, surface energies, and other relevant properties [3].

Table 1: Key Components of ReaxFF Methodology

Component Description Function
Bond Order Calculated from interatomic distances Determines bond strength and formation/breaking
Charge Equilibration Updated at each step Describes electrostatic interactions
Energy Contributions Multiple terms (bond, angle, torsion, etc.) Captures various chemical interactions
Parameterization Trained against QM data Ensures accuracy for specific chemical systems

Application Note: Lithium-Ion Diffusion in Battery Materials

Background and Significance

The study of lithium-ion diffusion in electrode materials is crucial for developing advanced batteries with improved performance and faster charging capabilities. ReaxFF enables researchers to simulate these processes at atomistic levels, providing insights that guide material design and optimization. This application note focuses on calculating diffusion coefficients of lithium ions in a Liâ‚€.â‚„S cathode material, following methodologies originally described in the publication "ReaxFF molecular dynamics simulations on lithiated sulfur cathode materials" [4].

Computational Workflow

The complete protocol for simulating lithium-ion diffusion coefficients involves multiple stages, from system preparation to data analysis. The following diagram illustrates the comprehensive workflow:

Diagram 1: ReaxFF workflow for diffusion coefficient calculation

Researcher's Toolkit: Essential Components

Table 2: Research Reagent Solutions for ReaxFF Diffusion Studies

Component Function Application Notes
AMS Software Suite Molecular dynamics simulation platform Provides ReaxFF engine integrated with analysis tools
LiS.ff Force Field Parameter set for Li-S systems Specifically parameterized for lithium-sulfur interactions
CIF Structure File Initial crystal structure α-Sulfur crystal as starting point for system construction
Grand Canonical Monte Carlo (GCMC) Alternative to random insertion More physically realistic insertion of Li atoms (optional)
AMSmovie Trajectory visualization and analysis Enables MSD and VACF calculations from MD trajectories
1,8-Octanediol1,8-Octanediol, CAS:629-41-4, MF:C8H18O2, MW:146.23 g/molChemical Reagent
Kaempferol 3-gentiobiosideKaempferol 3-gentiobioside, CAS:22149-35-5, MF:C27H30O16, MW:610.5 g/molChemical Reagent

Experimental Protocols

System Preparation and Equilibration

Importing Crystal Structure and Inserting Lithium Atoms
  • Open a new AMSinput window and switch to the ReaxFF engine.
  • Import the crystal structure: Select File → Import Coordinates and choose the CIF file for α-Sulfur.
  • Insert lithium atoms:
    • Click on Edit → Builder
    • Tick "Use number of molecules"
    • Set SMILES code to [Li] (including brackets)
    • Set N mols to 51 for Liâ‚€.â‚„S composition
    • Click "Generate Molecules" and then "Close" [4]
Geometry Optimization with Lattice Relaxation
  • Set calculation type: In the main panel, select Task → Geometry Optimization
  • Select force field: Click on the folder next to Force Field and select LiS.ff
  • Configure lattice optimization:
    • Go to Details → Geometry Optimization
    • Tick the "Optimize lattice" checkbox
  • Run the calculation:
    • Save the file with an appropriate name (e.g., "LiS_optimization")
    • Select File → Run
    • Update the structure in AMSinput when prompted [4]

Creating Amorphous Structure via Simulated Annealing

Amorphous structures are created using a molecular dynamics simulation with specific temperature cycling:

  • Set up molecular dynamics:

    • Select Task → Molecular Dynamics
    • Set the number of steps to 30000
    • Click next to Task: Molecular Dynamics for detailed settings

  • Configure temperature profile:

    • Click next to Thermostat for thermostat details
    • Add a new Berendsen thermostat
    • In Temperature(s), set: 300 300 1600 300
    • In Duration(s), set: 5000 20000 5000
    • Set damping constant to 100 fs [4]

  • Execute simulated annealing:

    • Save file as "LiSsimulatedannealing"
    • Run the calculation
    • Update structure when completed

This protocol creates the following temperature profile:

  • Steps 0-5000: Constant temperature at 300 K
  • Steps 5000-25000: Linear heating from 300 K to 1600 K
  • Steps 25000-30000: Rapid cooling from 1600 K to 300 K [4]

Production Simulation for Diffusion Analysis

  • Configure molecular dynamics:

    • Select Task → Molecular Dynamics
    • Set number of steps to 110000 (10000 equilibration + 100000 production)
    • Set Sample frequency to 5 (records positions and velocities every 5 steps)
    • Time step: 0.25 fs (default)

  • Set thermostat conditions:

    • Thermostat Type: Berendsen
    • Temperature: 1600 K
    • Clear the Duration field
    • Damping constant: 100 fs [4]

  • Run production simulation:

    • Save as "LiSMD1600K"
    • Execute calculation
    • Monitor progress in AMSMovie and AMStail

Data Analysis Methodologies

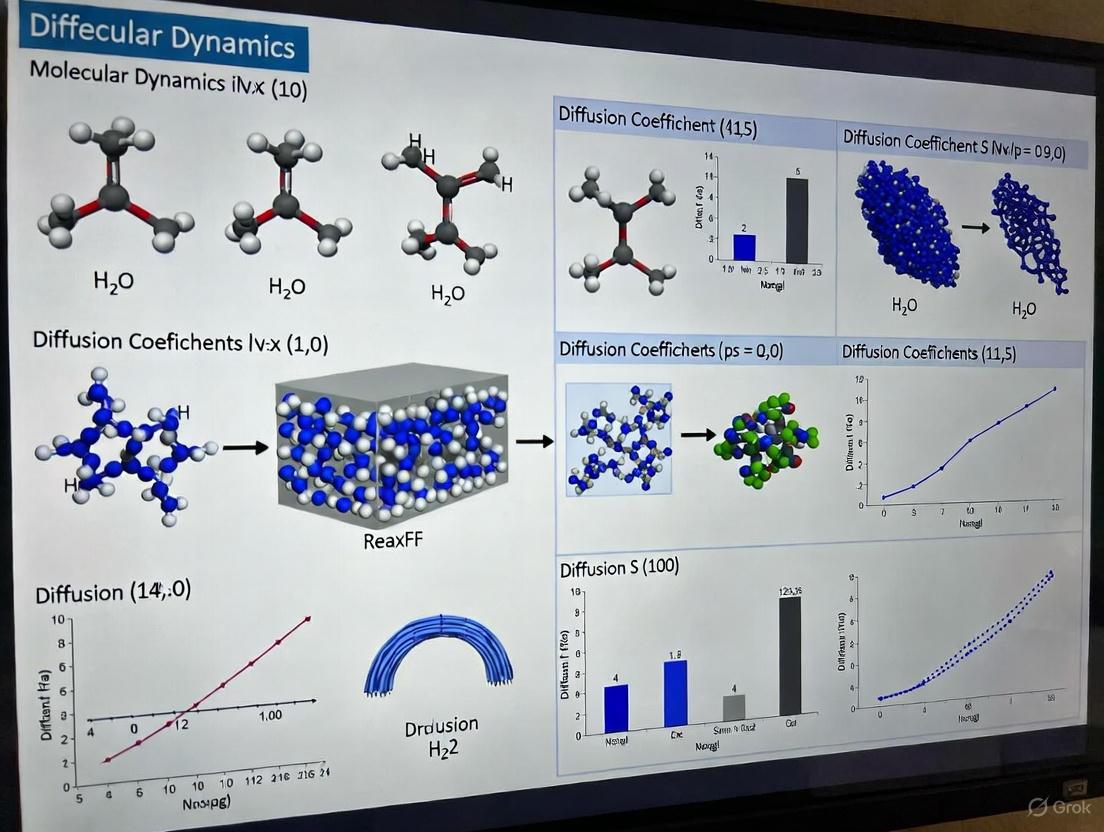
Mean Squared Displacement (MSD) Approach

The MSD method is the recommended approach for calculating diffusion coefficients:

  • Open the trajectory in AMSMovie
  • Access MSD analysis:
    • Select MD Properties → MSD
    • In Steps, set 2000 - 22001 (exclude equilibration)
    • Set Atoms to Li (select lithium atoms only)
    • Set Max MSD Frame to 5000 (corresponding to 5000 × 1.25 fs = 6250 fs)
  • Generate MSD: Click "Generate MSD" to calculate the mean squared displacement [4]

The diffusion coefficient is calculated from the slope of the MSD plot:

[ MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ]

[ D = \frac{\textrm{slope(MSD)}}{6} ]

The MSD should show a straight line, indicating normal diffusion behavior. If the MSD line is not straight, longer simulation times are needed to gather better statistics [4].

Velocity Autocorrelation Function (VACF) Method

The VACF approach provides an alternative method for diffusion coefficient calculation:

  • Open trajectory in AMSMovie
  • Access autocorrelation analysis:
    • Select MD Properties → Autocorrelation function
    • In Steps, set 2000 - 22001
    • Select Property → Diffusion Coefficient (D)
    • Set Atoms to Li
    • Set Max ACF Step to 5000
  • Generate ACF: Click "Generate ACF" to calculate the velocity autocorrelation function [4]

The diffusion coefficient is obtained through integration of the VACF:

[ D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t ]

The bottom plot shows the integral of the VACF divided by 3 (diffusion coefficient), which should converge to a horizontal line for sufficiently long times [4].

Quantitative Results and Method Comparison

Table 3: Diffusion Coefficient Results for Liâ‚€.â‚„S at 1600K

Method Diffusion Coefficient (m²/s) Convergence Behavior Computational Notes
MSD 3.09 × 10⁻⁸ Should be perfectly horizontal Requires straight MSD line for validity
VACF 3.02 × 10⁻⁸ Should converge for large times Requires small sampling frequency
Agreement Excellent (≈2% difference) Both methods show proper convergence MSD recommended for larger systems

Temperature Extrapolation using Arrhenius Relationship

For practical applications, diffusion coefficients at lower temperatures can be estimated through Arrhenius extrapolation:

  • Calculate D(T) at multiple temperatures: Perform production simulations at minimum four different temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K)
  • Construct Arrhenius plot: Plot ln(D(T)) against 1/T
  • Extract activation parameters: [ D(T) = D0 \exp{(-Ea / k{B}T)} ] [ \ln{D(T)} = \ln{D0} - \frac{Ea}{k{B}}\cdot\frac{1}{T} ] Where Dâ‚€ is the pre-exponential factor and E_a is the activation energy [4]

This approach enables estimation of room-temperature diffusion coefficients that would otherwise require prohibitively long simulation times due to reduced atomic mobility.

Technical Considerations and Best Practices

Finite-Size Effects and System Preparation

A critical consideration in ReaxFF diffusion studies is the management of finite-size effects:

  • System size dependence: Diffusion coefficients depend on supercell size unless the supercell is very large
  • Extrapolation procedure: Perform simulations for progressively larger supercells and extrapolate to the "infinite supercell" limit
  • Validation: Compare results from different system sizes to assess convergence [4]

Sampling and Statistical Accuracy

  • Trajectory length: Ensure sufficient sampling time for meaningful statistics
  • Equilibration exclusion: Exclude initial equilibration phase from analysis (e.g., first 2000 steps in the tutorial example)
  • Convergence monitoring: Check that MSD and VACF plots show proper convergence behavior
  • Multiple independent runs: Consider running multiple simulations with different initial random seeds for better statistics

Advanced Applications and Extensions

The ReaxFF methodology continues to evolve with several advanced capabilities:

  • eReaxFF: Explicit treatment of electrons enabling simulation of redox reactions
  • Acceleration techniques: Various methods for extending timescales, including collective variable-driven hyperdynamics
  • Reactive Monte Carlo: Grand Canonical Monte Carlo (GCMC) for improved system construction
  • Parameter optimization: Tools for refining force fields or building new ReaxFF parameter sets [5]

The protocols outlined in this application note for lithium-ion diffusion in sulfur cathodes can be adapted to study diffusion in various material systems, including other battery chemistries, polymer electrolytes, and catalytic systems.

Theoretical Basis of Diffusion Coefficients in Molecular Dynamics

The diffusion coefficient (D) is a critical transport property that quantifies the rate of particle movement through a material. In molecular dynamics (MD) simulations, calculating accurate diffusion coefficients is essential for researching and optimizing processes across numerous fields, including battery design, carbon sequestration, and drug development [6] [7]. MD simulations provide a robust computational framework that bridges microscopic particle motion with macroscopic transport properties, offering insights that are often challenging to obtain experimentally [6]. This article details the theoretical foundations, primary calculation methodologies, and practical protocols for determining diffusion coefficients, with a specific focus on applications within ReaxFF molecular dynamics simulations.

Theoretical Foundations

At the heart of diffusion coefficient calculations in MD lies the Einstein relation, which connects the random, microscopic motion of particles to a macroscopic diffusivity value [6]. This relation is operationalized through the calculation of the Mean Squared Displacement (MSD), defined as the average squared distance a particle travels over time:

[MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle]

where (\textbf{r}(0)) and (\textbf{r}(t)) are the particle's position vectors at time zero and time (t), respectively, and the angle brackets denote an average over all particles and time origins. For a particle undergoing normal diffusion, the MSD increases linearly with time. The slope of this linear relationship is directly proportional to the self-diffusion coefficient (D), which, in three dimensions, is given by:

[D = \frac{\textrm{slope(MSD)}}{6}]

An alternative, mathematically equivalent approach involves the Velocity Autocorrelation Function (VACF). The VACF measures how a particle's velocity at one time is correlated with its velocity at a later time. The diffusion coefficient is obtained from the integral of the VACF:

[D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t]

Where (\textbf{v}(t)) is the velocity vector at time (t). The MSD method is generally recommended for its straightforward implementation and robustness, whereas the VACF method can provide additional dynamical insights but may require higher data sampling rates [4].

Calculation Methodologies: MSD vs. VACF

The two primary methods for calculating diffusion coefficients from MD trajectories each have distinct advantages and considerations, as summarized in the table below.

Table 1: Comparison of Methods for Calculating Diffusion Coefficients from MD Simulations

Feature Mean Squared Displacement (MSD) Velocity Autocorrelation Function (VACF)
Theoretical Basis Einstein relation [6] Green-Kubo relation [6]
Recommended Use Primary, recommended method [4] Complementary method offering dynamical insights
Key Output Plot of MSD vs. time Plot of VACF, its integral, and power spectrum
Convergence (D) is derived from the slope of the linear portion of the MSD curve. (D) is derived from the plateau of the integrated VACF curve.
Sampling Requirement Lower sampling frequency is acceptable, leading to smaller trajectory files [4] Requires a high sampling frequency (small time steps between saved velocities) [4]
Computational Note The slope must be taken from the diffusive regime, after the initial ballistic motion. The integral should converge for large enough (t_{max}).

Practical Protocols for ReaxFF-MD

This section provides a detailed step-by-step protocol for calculating the diffusion coefficient of Lithium ions in an amorphous Li(_0.4)S cathode material using ReaxFF, as based on a established tutorial [4].

System Preparation and Equilibration
  • Structure Import and Construction: Begin by importing the crystal structure of the host material (e.g., a Sulfur crystal from a CIF file). Use the builder functionality in your MD software (e.g., AMSinput) to insert the diffusing species (e.g., 51 Li atoms) randomly into the structure. For more thermodynamically representative structures, consider using Grand Canonical Monte Carlo (GCMC) methods [4].
  • Geometry Optimization: Relax the initial structure by performing a geometry optimization with lattice relaxation. This crucial step minimizes high-energy atomic clashes and finds a stable starting configuration. Use an appropriate force field (e.g., LiS.ff for a Li-S system) [4].
  • Simulated Annealing for Amorphous Systems: To generate amorphous structures, perform a simulated annealing MD simulation.
    • Temperature Profile:
      • Step 0-5,000: Hold at 300 K.
      • Step 5,000-25,000: Ramp temperature from 300 K to 1600 K.
      • Step 25,000-30,000: Rapidly cool down from 1600 K to 300 K.
    • Thermostat: Use a Berendsen thermostat with a damping constant of 100 fs [4].
  • Final Optimization: After annealing, perform a second geometry optimization, including lattice relaxation, to obtain the final equilibrated amorphous structure for production MD runs.
Production MD Simulation
  • Simulation Setup: Configure an MD simulation at the target temperature (e.g., 1600 K for high-temperature studies).
    • Task: Molecular Dynamics.
    • Total Steps: 110,000 (including 10,000 steps for equilibration).
    • Thermostat: Berendsen thermostat at the target temperature with a damping constant of 100 fs.
    • Sample Frequency: Set to 5 (saving atomic positions and velocities every 5 steps). With a typical time step of 0.25 fs, this yields a trajectory output every 1.25 fs [4].
  • Execution: Run the simulation and monitor properties like temperature for stability.
Diffusion Coefficient Analysis

  • Via MSD (Recommended):

    • Load the production trajectory into an analysis tool (e.g., AMSmovie).
    • Select the relevant atoms (e.g., Li).
    • Calculate the MSD, setting the analysis to start after the equilibration period (e.g., from step 2,000).
    • Set a "Max MSD Frame" (e.g., 5,000) to analyze a sufficiently long time window (6,250 fs in this case).
    • The software will generate an MSD plot and a corresponding plot for (D), calculated as the slope of the MSD divided by 6. A constant (D) value indicates convergence [4].

  • Via VACF:

    • In the analysis tool, select the "Autocorrelation function" for the production phase of the trajectory.
    • Set the property to "Diffusion Coefficient (D)" and select the relevant atoms.
    • The tool will plot the VACF, its power spectrum, and the integral of the VACF divided by 3 (which is (D)). The value of (D) is taken from the plateau of this integral for large times [4].

The following workflow diagram illustrates the complete protocol from system setup to analysis.

Start Start: Import CIF File A Insert Li Ions (51 atoms via Builder/GCMC) Start->A B Geometry Optimization + Lattice Relaxation A->B C Simulated Annealing MD (Heat to 1600K, rapid cool) B->C D Final Geometry Optimization + Lattice Relaxation C->D E Production MD Simulation (1600K, 110,000 steps) D->E F Trajectory Analysis E->F G MSD Method F->G H VACF Method F->H I Output: D from slope(MSD)/6 G->I J Output: D from ∫VACF/3 H->J

Diagram 1: Complete workflow for calculating diffusion coefficients in battery cathode materials.

Essential Considerations and Best Practices

Addressing Computational Artifacts

Obtaining physically meaningful diffusion coefficients requires careful consideration of several computational factors.

  • Finite-Size Effects: The calculated diffusion coefficient is sensitive to the size of the simulation cell. To mitigate this, perform simulations for progressively larger supercells and extrapolate the calculated (D) values to the "infinite supercell" limit [4].
  • Ballistic vs. Diffusive Regime: At very short timescales, particle motion is ballistic (MSD (\propto t^2)), not diffusive. The linear slope used to calculate (D) must be taken from the subsequent diffusive regime (MSD (\propto t)). Running a sufficiently long simulation is necessary to capture this [6].
  • Force Field Selection and Parameterization: The choice of force field is critical. Standard force fields may not accurately capture the solid nature and mass transport properties of all materials. For instance, a reparameterization of ReaxFF for Lithium Fluoride (LiF) was necessary to correct the diffusivity of lithium ions by two orders of magnitude at room temperature, making the prediction realistic [8]. Always validate your force field for the specific system and property of interest.

Table 2: Key Research Reagent Solutions for ReaxFF-MD Diffusion Studies

Reagent / Tool Function / Description Example Use Case
ReaxFF Force Field A reactive force field using bond-order and charge equilibration to model chemical reactions. Simulating electrolyte decomposition and Li-ion diffusion in batteries [8].
AMSinput / AMSmovie Software for setting up MD simulations and analyzing trajectories. Importing structures, building systems, and calculating MSD/VACF [4].
Python Libraries (ASE, PyMatgen) Libraries for automating and orchestrating atomistic simulations. Managing simulation workflows and facilitating force field reparameterization [8].
Berendsen Thermostat An algorithm to control the simulation temperature by weakly coupling the system to a heat bath. Maintaining temperature during equilibration and production MD runs [4].
Extrapolation to Experimental Conditions

Directly calculating (D) at low temperatures (e.g., room temperature) can be computationally prohibitive due to slow dynamics. A common strategy is to use the Arrhenius equation to extrapolate from higher-temperature simulations:

[D(T) = D0 \exp{(-Ea / k_{B}T)}]

where (D0) is the pre-exponential factor, (Ea) is the activation energy, (kB) is the Boltzmann constant, and (T) is the temperature. By calculating (D) for at least four different elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) and plotting (\ln{(D(T))}) against (1/T), one can determine (Ea) and (D_0) from the slope and intercept, allowing for the estimation of (D) at lower, experimentally relevant temperatures [4]. The diagram below illustrates this analytical workflow.

Start Perform MD Simulations at Multiple Temperatures A Calculate D at each T (via MSD or VACF) Start->A B Plot ln(D) vs. 1/T (Arrhenius Plot) A->B C Perform Linear Fit B->C D Extract Ea from slope and D0 from intercept C->D E Extrapolate D to lower T using Arrhenius equation D->E

Diagram 2: Workflow for extrapolating diffusion coefficients using Arrhenius behavior.

Molecular dynamics simulations, particularly using reactive force fields like ReaxFF, provide a powerful tool for determining diffusion coefficients atomistically. The MSD method offers a robust and recommended pathway for calculating (D), while the VACF method serves as a valuable complementary approach. The accuracy of these calculations hinges on careful system preparation, including equilibration and annealing, and a thorough understanding of computational limitations such as finite-size effects and force field applicability. By adhering to the detailed protocols outlined herein and leveraging strategies like Arrhenius extrapolation, researchers can reliably simulate and predict diffusion coefficients, thereby enabling advances in material design and optimization for energy storage and other critical technologies.

Application Notes

The ReaxFF reactive force-field is a powerful computational tool for modeling complex, dynamic chemical processes across diverse material systems, bridging the gap between quantum mechanical accuracy and classical molecular dynamics scale. By employing a bond-order formalism, ReaxFF enables the simulation of reactive events, making it uniquely suited for investigating phenomena in battery materials, combustion chemistry, and biomolecular transport where bond formation and breaking are central [2]. Its functional form describes the system energy through a combination of bond-order-dependent and bond-order-independent terms, allowing for the simulation of reactive interfaces between solid, liquid, and gas phases [2].

Battery Materials

In lithium-ion battery (LIB) research, ReaxFF is instrumental in studying the formation, composition, and properties of the solid-electrolyte interphase (SEI), a critical passivation layer that forms on anode surfaces. The SEI governs battery performance, cycle life, and safety, but its reactive and multiscale nature makes it difficult to study experimentally [8]. ReaxFF molecular dynamics (MD) simulations have provided insights into the layering of organic and inorganic SEI components resulting from electrolyte decomposition on lithium metal and graphite anodes [8]. A key focus of recent development has been enhancing force fields for specific SEI components like Lithium Fluoride (LiF), which is known to improve cycling stability due to its high ion transport and electronic insulation properties [8]. Furthermore, ReaxFF can be used to compute lithium ion diffusion coefficients within electrode materials, a critical parameter for battery performance, typically through analysis of the mean squared displacement (MSD) from MD trajectories [4].

Combustion Systems

ReaxFF enables the detailed study of complex reaction pathways and kinetics in combustion processes at the atomic scale. It has been successfully applied to simulate the combustion of hydrocarbons, such as methane, revealing the consumption of reactants and the production of species like Hâ‚‚O and COâ‚‚ [9]. The force field's transferability across phases allows it to model the interaction of gaseous oxidizers with solid or liquid fuels. Recent studies have extended this capability to more complex systems, such as the hydrothermal gasification of polystyrene microplastics, elucidating the crucial roles of temperature and water content in syngas production and reaction mechanisms [10]. Similarly, ReaxFF MD simulations have been used to investigate the sintering and oxidation characteristics of aluminum nanoparticles (ANPs), providing molecular-level understanding of how hydrocarbon coatings can modulate reactivity and improve combustion performance [11].

Biomolecular Transport

Modeling biomolecular transport presents a significant challenge for reactive force fields. While ReaxFF's formal framework could, in principle, be applied to complex biological molecules, the available literature and parameterizations are predominantly focused on materials science, battery research, and combustion chemistry. The primary challenge lies in the lack of specific, optimized force field parameters for key biological elements and complex molecular interactions. Current research, as identified, does not provide specific application notes for this sub-topic, indicating a potential area for future ReaxFF development.

Table 1: Key Application Areas of ReaxFF MD Simulations

Application Area System of Interest ReaxFF's Role Key Insights
Battery Materials Li-ion batteries (Anodes, SEI) Models electrolyte reduction and SEI formation & properties [8]. Revealed layered SEI structure; LiF-rich SEI improves stability [8].
Combustion Systems Hydrocarbons (e.g., Methane), Energetic materials (e.g., ANPs) Uncovers detailed reaction pathways and kinetics under extreme conditions [9] [10] [11]. Identified reaction products (Hâ‚‚O, COâ‚‚); showed coating controls ANP reactivity [9] [11].
Biomolecular Transport Not specified in search results Potential to model reactive processes in biomolecules. Lacks specific parameterization and application data in current literature.

Experimental Protocols

The following protocols provide detailed methodologies for setting up and analyzing ReaxFF MD simulations for computing diffusion coefficients in battery materials and for studying combustion reactions.

Protocol 1: Calculating Diffusion Coefficients in Battery Electrode Materials

This protocol outlines the procedure for computing the diffusion coefficient (D) of lithium ions in a model cathode material (e.g., Li~0.4~S) using ReaxFF MD, based on a documented tutorial [4].

Workflow Overview:

DCA Start Start: Import CIF File A Generate Structure (e.g., Insert Li atoms) Start->A B Geometry Optimization with Lattice Relaxation A->B C Simulated Annealing (Create amorphous structure) B->C D Final Geometry Optimization C->D E Production MD Run at Target Temperature D->E F Trajectory Analysis (MSD or VACF) E->F G Calculate Diffusion Coefficient (D) F->G End End: Result D G->End

Materials and Setup:

  • Software: AMS software suite (including AMSinput, AMSmovie, AMSjobs) [4].
  • Force Field: An appropriate ReaxFF parameter file (e.g., LiS.ff for lithium-sulfur systems) [4].
  • Initial Structure: A crystallographic information file (.cif) for the base cathode material.

Step-by-Step Procedure:

  • System Preparation:

    • Import the cathode material's CIF file into AMSinput.
    • Use the Builder tool to insert the required number of Li atoms (e.g., 51 Li atoms for Li~0.4~S) randomly into the structure using the SMILES code [Li] [4].
    • Set the calculation Task to Geometry Optimization.
    • Select the relevant force field (e.g., LiS.ff).
    • In the Details → Geometry Optimization panel, tick Optimize lattice.
    • Run the calculation and update the AMSinput structure upon completion [4].

  • Creating an Amorphous Structure (Simulated Annealing):

    • Change the Task to Molecular Dynamics.
    • Set the number of steps (e.g., 30,000) and the Thermostat to Berendsen.
    • Configure a temperature profile for annealing:
      • Temperature(s): 300 300 1600 300 K
      • Duration(s): 5000 20000 5000 steps
    • Run the simulation and update the structure upon completion [4].
    • Perform a final Geometry Optimization with Optimize lattice checked to relax the annealed structure [4].

  • Production MD Simulation:

    • Set the Task to Molecular Dynamics.
    • Set the Number of steps (e.g., 110,000 for equilibration + production).
    • Set the Sample frequency (e.g., 5) to write trajectory data regularly.
    • Configure the Thermostat (e.g., Berendsen) for a constant target temperature (e.g., 1600 K).
    • Run the production MD simulation [4].

  • Data Analysis - Diffusion Coefficient:

    • Via Mean Squared Displacement (MSD - Recommended):
      • Open the trajectory in AMSmovie.
      • Select MD Properties → MSD.
      • Set the Atoms to Li.
      • Adjust the Steps and Max MSD Frame to select a stable, linear region of the MSD plot.
      • Click Generate MSD. The software will perform a linear fit.
      • Calculate ( D = \frac{\text{slope(MSD)}}{6} ) [4].
    • Via Velocity Autocorrelation Function (VACF):
      • In AMSmovie, select MD Properties → Autocorrelation function.
      • Set Property to Diffusion Coefficient (D) and Atoms to Li.
      • Click Generate ACF. The value of D is obtained from the plateau in the bottom plot (integral of VACF divided by 3) [4].

Troubleshooting and Validation:

  • Finite-Size Effects: The calculated diffusion coefficient is sensitive to supercell size. For accurate results, perform simulations for progressively larger supercells and extrapolate to the "infinite supercell" limit [4].
  • Statistical Accuracy: Ensure the MSD plot shows a clear linear regime. A curved or noisy MSD indicates the need for a longer simulation to gather better statistics [4].
  • Convergence Check: The diffusion coefficient (D) curve derived from the VACF integral should become horizontal (converge) for large times [4].

Protocol 2: Simulating a Combustion Reaction

This protocol describes how to set up and analyze a ReaxFF MD simulation for a gas-phase combustion reaction, using a methane (CHâ‚„) and oxygen (Oâ‚‚) mixture as an example [9].

Workflow Overview:

CRA Start Start: New Input in AMSinput A Build Mixture (Set density and mole fractions) Start->A B Select Force Field (e.g., CHO.ff) A->B C Configure MD (High T, Nose-Hoover Thermostat) B->C D Run Simulation C->D E Monitor Progress (in AMSmovie and logfile) D->E F Analyze Products (Molecule identification) E->F End End: Reaction Profile F->End

Materials and Setup:

  • Software: AMS software suite [9].
  • Force Field: A force field parameterized for combustion (e.g., CHO.ff for hydrocarbon oxidation) [9].
  • System: A mixture of fuel and oxidizer (e.g., CHâ‚„ and Oâ‚‚).

Step-by-Step Procedure:

  • Build the Reactant Mixture:

    • In AMSinput, set Periodicity to Bulk.
    • Open the Builder (Edit → Builder).
    • Set the Density (e.g., 1.163 g/cm³ for a high-density, fast simulation).
    • Set the Approximate number of atoms (e.g., 500).
    • Tick Use mole fractions.
    • Add rows for the fuel and oxidizer. Specify them using SMILES codes or searches (e.g., CHâ‚„ and Oâ‚‚) and set their mole fractions (e.g., a 1:2.5 ratio for CHâ‚„:Oâ‚‚).
    • Click Generate Molecules and then Close [9].

  • Configure the MD Simulation:

    • Select the appropriate Force Field (e.g., CHO.ff).
    • Set the Task to Molecular Dynamics.
    • In the MD settings, set the Number of steps (e.g., 30,000).
    • Configure the Thermostat:
      • Select NHC (Nose-Hoover Chain) for better sampling.
      • Set a high Temperature (e.g., 3500 K to accelerate reactions).
      • Set a Damping constant (e.g., 100 fs) [9].

  • Run and Monitor the Simulation:

    • Run the calculation. The simulation can be monitored in real-time.
    • Open AMSmovie (SCM → Movie) to visualize the trajectory as it runs.
    • Use MD Properties → Temperature and MD Properties → Conserved Energy to monitor thermodynamic stability [9].

  • Analyze Reaction Products:

    • In AMSmovie, use MD Properties → Molecules… to open the molecule analysis dialog.
    • This dialog lists all molecule types detected during the simulation. To refresh the list for a running job, close and reopen the dialog.
    • Select the checkboxes for key reactants and products (e.g., CHâ‚„, Oâ‚‚, Hâ‚‚O, COâ‚‚) to plot their counts over time.
    • Use the visualization tools in conjunction with the molecule plot: click on a data point in the plot to jump to that frame in the trajectory and visually inspect the corresponding molecular species [9].

Troubleshooting and Validation:

  • Lack of Reaction: If no reactions occur within the simulated timeframe, consider increasing the temperature (though this reduces physical realism) or the simulation length.
  • Identifying Products: The automatic molecule identification may sometimes group atoms incorrectly. Cross-referencing with the visualizer is crucial for validation.

The Scientist's Toolkit

This section details key resources and materials required for conducting ReaxFF MD simulations in the discussed application areas.

Table 2: Essential Research Reagent Solutions for ReaxFF Simulations

Item Name Function / Description Example / Specification
ReaxFF Force Field Parameter File Contains all empirical parameters defining atomic interactions for a specific set of elements. It is the core of the simulation. CHO.ff (for hydrocarbon oxidation) [9], LiS.ff (for lithium-sulfur systems) [4].
Initial Coordinate File Defines the starting atomic positions and, for crystalline materials, the unit cell. Crystallographic Information File (.cif) [4], XYZ file [4], or PDB file.
Molecular Builder Tool Software component for constructing complex molecular systems, inserting species, and creating mixtures. AMSinput Builder [4] [9].
Trajectory Analysis & Visualization Software Essential for visualizing simulation progress, analyzing results, and calculating properties like MSD, VACF, and molecule counts. AMSmovie [4] [9].
High-Performance Computing (HPC) Cluster ReaxFF MD simulations are computationally intensive and typically require parallel computing resources to run in a reasonable time. A cluster with multiple CPU cores and sufficient RAM [9].
DotmpDotmp, CAS:91987-74-5, MF:C12H32N4O12P4, MW:548.30 g/molChemical Reagent
Hexanoic anhydrideHexanoic anhydride, CAS:2051-49-2, MF:C12H22O3, MW:214.30 g/molChemical Reagent

The Reactive Force-Field (ReaxFF) interatomic potential is a powerful computational tool for exploring, developing and optimizing material properties, bridging the gap between highly accurate but computationally expensive quantum mechanical (QM) methods and efficient but non-reactive classical potentials [2]. ReaxFF achieves this by employing a bond-order formalism that allows for dynamic bond formation and breaking, enabling the simulation of chemical reactions without the prohibitive computational cost of QM methods [2]. This capability makes ReaxFF particularly valuable for studying complex reactive processes in materials science, including the diffusion of species through various phases, which is a central theme in molecular dynamics diffusion research [2] [4].

The fundamental strength of ReaxFF lies in its transferability across different phases—an oxygen atom is treated with the same mathematical formalism whether it is in the gas phase as O₂, in the liquid phase within an H₂O molecule, or incorporated in a solid oxide [2]. This transferability, coupled with its ability to handle reactive events, makes it ideally suited for investigating diffusion phenomena in complex, multi-phase systems where chemical reactions and mass transport are interconnected.

The Bond-Order Formalism

At the heart of the ReaxFF method is its bond-order formalism, which implicitly describes chemical bonding without expensive QM calculations [2]. Unlike traditional force fields that require predefined connectivity, ReaxFF calculates bond order (BO) directly and continuously from interatomic distances using an empirical formula:

[BO{ij} = BO{ij}^\sigma + BO{ij}^\pi + BO{ij}^{\pi\pi} = \exp\left[p{bo1}\left(\frac{r{ij}}{r0^\sigma}\right)^{p{bo2}}\right] + \exp\left[p{bo1}\left(\frac{r{ij}}{r0^\pi}\right)^{p{bo4}}\right] + \exp\left[p{bo1}\left(\frac{r{ij}}{r0^{\pi\pi}}\right)^{p{bo6}}\right]]

In this formulation, BOᵢⱼ represents the total bond order between atoms i and j, which is the sum of σ, π, and ππ components [2]. The rᵢⱼ term is the interatomic distance, r₀ terms represent equilibrium bond lengths for different bond types, and pbo terms are empirical parameters. This continuous, distance-dependent calculation of bond order allows ReaxFF to naturally handle bond formation, dissociation, and transitions between single, double, and triple bonds without introducing discontinuities in the potential energy surface [2].

This approach provides a differentiable potential energy surface essential for calculating interatomic forces during molecular dynamics simulations [2]. The bond order is typically calculated within a covalent range of approximately 5 Ã…ngstroms, which is sufficient to capture even the weakest covalent interactions for most elements [2].

Comprehensive Energy Contributions

The ReaxFF potential energy is described as a sum of various energy contributions that collectively determine the system's behavior [2]:

[E{system} = E{bond} + E{over} + E{angle} + E{tors} + E{vdWaals} + E{Coulomb} + E{Specific}]

The following table summarizes these key energy terms and their physical significance in the ReaxFF potential:

Table 1: Energy Contributions in the ReaxFF Potential

Energy Term Symbol Description Physical Significance
Bond Energy Ebond Energy associated with bond formation/breaking Describes covalent interactions through bond-order formalism
Overcoordination Penalty Eover Energy penalty preventing atom overcoordination Based on atomic valence rules; prevents unrealistic bonding
Angle Strain Eangle Three-body valence angle strain energy Maintains proper molecular geometry
Torsional Strain Etors Four-body torsional angle strain energy Governs rotational barriers around bonds
van der Waals EvdWaals Dispersive interactions Calculated between all atom pairs regardless of connectivity
Coulomb ECoulomb Electrostatic interactions Calculated between all atoms using charge equilibration
Specific Terms ESpecific System-specific corrections Includes lone-pair, conjugation, hydrogen binding corrections

These energy terms can be conceptually divided into bond-order-dependent contributions (Ebond, Eover, Eangle, Etors) and bond-order-independent contributions (EvdWaals, ECoulomb) [2]. The non-bonded interactions, EvdWaals and ECoulomb, are calculated between all atoms irrespective of connectivity, which is crucial for properly describing intermolecular interactions in diffusion processes [2].

The ESpecific term represents system-specific corrections that are not generally included unless required to capture properties particular to the system of interest, such as lone-pair interactions, conjugation effects, hydrogen binding, and Câ‚‚ corrections [2].

Computational Protocols for Diffusion Studies

The calculation of diffusion coefficients using ReaxFF molecular dynamics involves several well-defined steps, from system preparation to production simulations and analysis. The following workflow outlines the key stages in a typical diffusion study:

G Start Start: System Preparation Step1 1. Structure Import & Initial Optimization Start->Step1 Step2 2. System Construction & Equilibration Step1->Step2 Step3 3. Simulated Annealing (For Amorphous Systems) Step2->Step3 Step4 4. Production MD Simulation Step3->Step4 Step5 5. Diffusion Coefficient Calculation Step4->Step5 Step6 6. Multi-Temperature Extrapolation Step5->Step6 End Final Result: Diffusion Coefficient at Target T Step6->End

System Preparation and Equilibration Protocol

Structure Import and Initial Optimization:

  • Begin by importing the initial crystal structure, typically from a CIF file [4].
  • Perform geometry optimization including lattice relaxation using an appropriate ReaxFF force field [4].
  • For battery materials like LixS, use the Builder functionality to insert mobile ions (e.g., Li-atoms) randomly into the structure [4].
  • Optimize the structure again with lattice relaxation to accommodate the inserted species [4].

Creating Amorphous Systems by Simulated Annealing:

  • For materials that require modeling in amorphous states, implement a simulated annealing protocol [4]:
    • Perform Molecular Dynamics with the following temperature profile:
      • From start until step 5000: Maintain constant temperature at 300 K
      • From step 5000 to step 25000: Heat linearly from 300 K to 1600 K
      • From step 25000 to step 30000: Cool rapidly from 1600 K to 300 K [4]
    • Use a Berendsen thermostat with a damping constant of 100 fs [4]
    • Follow annealing with final geometry optimization including lattice relaxation [4]

Production Simulation and Analysis Protocol

Production MD Simulation Setup:

  • Configure Molecular Dynamics for production run:
    • Set total steps to 110,000 (10,000 equilibration + 100,000 production) [4]
    • Set sampling frequency to 5 (records positions and velocities every 5 steps) [4]
    • Use Berendsen thermostat at target temperature (e.g., 1600 K) [4]
    • Set damping constant to 100 fs [4]
  • The time between trajectory points will be: samplefrequency × timestep = 5 × 0.25 fs = 1.25 fs [4]

Diffusion Coefficient Calculation Methods:

Two primary methods are used to compute diffusion coefficients from MD trajectories:

Method 1: Mean Squared Displacement (MSD) - Recommended

  • Calculate MSD using the formula: [MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle]
  • Compute diffusion coefficient as: [D = \frac{\textrm{slope(MSD)}}{6}]
  • In practice:
    • Set analysis for appropriate steps (e.g., 2000-22001)
    • Select diffusing atoms (e.g., Li)
    • Set maximum MSD frame to 5000 (corresponding to 5000×1.25 fs = 6250 fs) [4]
  • The diffusion coefficient is determined from the linear region of the MSD vs. time plot [4]

Method 2: Velocity Autocorrelation Function (VACF)

  • Calculate VACF and integrate to obtain diffusion coefficient: [D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t]
  • This method requires higher sampling frequency (smaller interval between saved frames) [4]

Extrapolation to Lower Temperatures:

  • Calculate diffusion coefficients at multiple elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) [4]
  • Use Arrhenius equation for extrapolation: [D(T) = D0 \exp{(-Ea / k{B}T)}] [\ln{D(T)} = \ln{D0} - \frac{Ea}{k{B}}\cdot\frac{1}{T}]
  • Create Arrhenius plot of ln(D(T)) against 1/T to determine activation energy (Ea) and pre-exponential factor (D0) [4]
  • Extrapolate to predict diffusion coefficients at lower temperatures inaccessible to direct MD simulation [4]

Essential Research Reagents and Computational Tools

Successful implementation of ReaxFF diffusion studies requires careful selection of force fields and computational tools. The following table details key "research reagent solutions" essential for these simulations:

Table 2: Essential Research Reagents and Computational Tools for ReaxFF Diffusion Studies

Tool/Reagent Type Function Application Notes
CHO.ff Force Field Describes hydrocarbon oxidation Part of combustion branch; parameters from Chenoweth et al. [12]
CuCl-Hâ‚‚O.ff Force Field Models aqueous chloride/copper chloride Part of water branch; for aqueous systems [12]
FeOCHCl.ff Force Field Simulates iron-oxyhydroxide systems Contains Fe/O/C/H/Cl parameters; water branch [12]
LiS.ff Force Field Specific for lithium-sulfur systems Used in battery material diffusion studies [4]
AMSinput Software Graphical interface for simulation setup Provides Builder functionality for system construction [4]
LAMMPS Software Open-source MD engine Supports ReaxFF implementation [2]
PuReMD Software Purdue Reactive MD code Optimized for ReaxFF simulations [2]
AMSmovie Analysis Tool Visualization and analysis of MD trajectories Calculates MSD, VACF, diffusion coefficients [4]

Critical Implementation Considerations

Force Field Selection: ReaxFF parameters are typically divided into two major branches: the combustion branch and the aqueous (water) branch [12]. The primary difference lies in the O/H parameters, where the combustion branch focuses on accurately describing water as a gas-phase molecule, while the water branch targets aqueous chemistry [12]. Selection should be based on the specific system and phase conditions being studied.

Finite-Size Effects:

  • Diffusion coefficients calculated from MD simulations exhibit finite-size effects dependent on supercell size [4]
  • For accurate results, perform simulations with progressively larger supercells
  • Extrapolate calculated diffusion coefficients to the "infinite supercell" limit [4]

Convergence Criteria:

  • For MSD analysis: The slope of MSD vs. time should be linear in the diffusion regime [4]
  • For VACF analysis: The integral of VACF divided by 3 should converge to a constant value [4]
  • If these criteria are not met, longer simulations are required to gather better statistics [4]

Advanced Applications and Recent Developments

Recent advancements in ReaxFF have expanded its applications to complex bimetallic systems relevant to catalysis and energy materials. For instance, parameters have been developed for MnMOx (M = Cu, Fe, Ni) bimetallic transition-metal oxides, enabling the study of toluene adsorption and degradation on catalyst surfaces [13]. The development process for these force fields involves:

  • Training against DFT data and experimental results
  • Geometry optimization using multiple temperature regimes (1 K, 300 K, 500 K)
  • Validation through comparison of ReaxFF-obtained geometries with crystallographic data [13]

While ReaxFF has proven successful in numerous applications, recent developments in neural network potentials (NNPs) like EMFF-2025 offer promising alternatives that may achieve higher accuracy while maintaining computational efficiency for C, H, N, O-based systems [14]. However, ReaxFF remains a robust and widely-used method for simulating reactive processes, particularly for complex multi-element systems and diffusion studies where chemical reactivity and mass transport are coupled.

Within the broader context of ReaxFF molecular dynamics (MD) tutorial research, particularly for calculating material properties like diffusion coefficients in battery materials, a robust system preparation workflow is a critical first step [4]. The accuracy of subsequent MD simulations hinges on the quality of the initial structural model and its careful relaxation to a stable, low-energy configuration. This protocol details the comprehensive procedure for preparing an atomistic system, using a lithiated sulfur cathode (Li~0.4~S) as a representative example, from the initial import of a crystal structure to the final relaxed structure ready for production MD simulations [4]. The methodology is adapted from established ReaxFF research on lithiated sulfur cathode materials [4] [15].

The Scientist's Toolkit: Essential Research Reagents and Software

The following table catalogues the key computational "reagents" and tools required to execute the system preparation workflow.

Table 1: Essential Research Reagents and Software Solutions

Item Function in the Workflow Specific Example / Note
CIF File Provides the initial, experimentally determined crystal structure of the host material. Alpha-sulfur (S~8~) structure from a crystallographic database [4] [15].
ReaxFF Force Field An empirical potential that describes interatomic interactions, enabling modeling of bond breaking and formation. LiS.ff parameter set, trained for lithium-sulfur systems [4] [15].
MD Software Package The simulation engine that performs energy calculations, geometry optimization, and molecular dynamics. Amsterdam Modeling Suite (AMS) with ReaxFF module [4] [5]; other options include LAMMPS [2].
Builder/Visualization Tool Used for manipulating atomic structures (e.g., inserting atoms, building supercells) and visualizing results. AMSinput builder [4]; OVITO for trajectory analysis [16].
BimoclomolBimoclomolBimoclomol is a heat shock protein co-inducer that activates HSF1 for research on neuroprotection, cytoprotection, and lysosomal function. For Research Use Only. Not for human use.
IliparcilIliparcil, CAS:137214-72-3, MF:C16H18O6S, MW:338.4 g/molChemical Reagent

The entire system preparation process, from initial CIF import to a finalized structure, can be visualized as a sequential workflow. The following diagram outlines the key stages and decision points.

Start Start: Obtain CIF File A Import CIF into Simulation Environment Start->A B Generate System via Builder or GCMC A->B C Initial Geometry Optimization B->C D Simulated Annealing for Amorphization C->D E Final Geometry & Lattice Relaxation D->E End End: Relaxed Structure E->End

Diagram 1: The overall system preparation workflow for ReaxFF simulations.

Detailed Experimental Protocols

Phase 1: Initial Structure Import and System Generation

Objective: To acquire a starting crystal structure and generate the desired chemical system, such as Li~x~S.

  • Importing the CIF File:

    • Open a new document in your simulation environment's input utility (e.g., AMSinput) [4].
    • Navigate to File → Import Coordinates and select the downloaded CIF file (e.g., for α-sulfur) [4]. The crystal structure will be loaded into the viewer.

  • Generating the Li~0.4~S System:

    • Access the builder functionality (Edit → Builder) [4].
    • In the builder menu, select to use a specific number of molecules.
    • In the SMILES or xyz-file field, enter [Li] to represent a single lithium atom.
    • Set the number of molecules (N mols) to the required quantity (e.g., 51 Li atoms for a specific S structure) and click Generate Molecules [4]. The Li atoms will be randomly inserted into the sulfur structure.
    • Alternative Advanced Method: For a more thermodynamically realistic distribution, Grand Canonical Monte Carlo (GCMC) can be used instead of random insertion to introduce lithium atoms [4] [15].

Phase 2: Structure Relaxation and Equilibration

Objective: To relax the generated system's geometry and lattice, relieving any steric clashes or high-energy configurations introduced during the building process.

  • Initial Geometry and Lattice Optimization:
    • In the main panel of your input utility, set the Task to Geometry Optimization [4].
    • Select the appropriate ReaxFF force field (e.g., LiS.ff) [4].
    • Navigate to the Details → Geometry Optimization panel and enable the Optimize lattice checkbox. This allows the simulation cell's size and shape to change during minimization [4].
    • Save and run the calculation. Upon completion, update the structure in the input utility with the optimized coordinates [4].

Phase 3: Creating Amorphous Structures (Optional)

Objective: To generate an amorphous phase of the material through a simulated annealing process, which may be more representative of certain experimental conditions.

  • Setting Up Simulated Annealing:

    • Change the Task to Molecular Dynamics [4].
    • In the MD details, set the number of steps (e.g., 30,000 for a short demonstration) [4].
    • Configure the temperature profile (thermostat) to achieve annealing [4]:
      • Add a Berendsen thermostat.
      • Set Temperature(s) to 300 300 1600 300 (in Kelvin).
      • Set Duration(s) for these regimes to 5000 20000 5000 (in steps).
      • This profile holds at 300 K, ramps to 1600 K, then rapidly quenches back to 300 K.
    • Run the simulation and update the input structure with the final coordinates from the trajectory [4].

  • Relaxing the Amorphous System:

    • Perform a final Geometry Optimization (with Optimize lattice enabled) on the annealed structure to relax it into a low-energy amorphous configuration [4].

Quantitative Parameters for Simulation Setup

The tables below summarize critical numerical parameters for the key simulation steps in this workflow.

Table 2: Molecular Dynamics Parameters for Simulated Annealing

Parameter Value Purpose / Note
Total Steps 30,000 [4] Defines the total simulation length.
Temperature Regime 300 K → 1600 K → 300 K [4] Heats the crystal to induce disorder, then rapidly cools to "freeze" in the amorphous state.
Damping Constant 100 fs [4] Controls the strength of coupling to the thermostat.

Table 3: Energy Minimization Settings

Parameter Setting Purpose / Note
Task Geometry Optimization [4] To find the nearest local energy minimum.
Lattice Optimization Enabled [4] Crucial for relieving internal pressure and allowing volume changes upon lithiation.
Force Field System-specific (e.g., LiS.ff) [4] Must be parameterized for all elements and interactions in the system.

This application note has provided a detailed, step-by-step protocol for preparing complex material systems for ReaxFF molecular dynamics studies. By meticulously following the stages of CIF import, system generation, structure relaxation, and optional amorphization, researchers can create robust and reliable initial conditions. This rigorous approach to system preparation lays the essential groundwork for obtaining physically meaningful results in subsequent analyses, such as the calculation of ion diffusion coefficients in energy storage materials [4]. The principles outlined here, while demonstrated for a Li-S battery material, are broadly transferable to other classes of materials investigated with reactive force fields.

Choosing Appropriate Force Fields for Your Chemical System

In atomistic simulations, a force field is a set of parameters and equations used to compute forces between atoms and molecules, enabling the prediction of material behavior and properties. The Reactive Force Field (ReaxFF) method represents a significant advancement in molecular simulation techniques, bridging the gap between highly accurate but computationally expensive quantum mechanics (QM) methods and efficient but non-reactive classical force fields. Developed by Adri van Duin and colleagues, ReaxFF has become a powerful computational tool for exploring, developing, and optimizing material properties across diverse research domains [2] [17].

Unlike classical force fields that rely on predefined connectivity between atoms, ReaxFF employs a bond-order formalism that dynamically describes chemical bonding without expensive QM calculations. This innovative approach allows ReaxFF to simulate reactive events—the making and breaking of chemical bonds—during molecular dynamics simulations, while maintaining computational efficiency for large-scale systems [2]. The method has demonstrated remarkable transferability across the periodic table, with parameters available for elements ranging from hydrocarbons to transition metals and complex material systems.

The total energy in ReaxFF is partitioned into several components that collectively describe the complex interactions within chemical systems:

[ E{\text{system}} = E{\text{bond}} + E{\text{over}} + E{\text{angle}} + E{\text{tors}} + E{\text{vdWaals}} + E{\text{Coulomb}} + E{\text{Specific}} ]

Where (E{\text{bond}}) represents bond energy, (E{\text{over}}) is an energy penalty for over-coordination, (E{\text{angle}}) and (E{\text{tors}}) describe angle and torsion strain, (E{\text{vdWaals}}) and (E{\text{Coulomb}}) account for non-bonded interactions, and (E_{\text{Specific}}) includes system-specific terms such as lone-pair energies and conjugation effects [2]. This comprehensive energy description enables ReaxFF to accurately model both covalent and electrostatic interactions for a diverse range of materials, making it particularly valuable for studying complex processes at interfaces between solid, liquid, and gas phases.

Key Considerations for Force Field Selection

Selecting an appropriate force field is critical for obtaining reliable simulation results in computational chemistry and materials science. The choice depends on multiple factors, including the chemical composition of your system, the processes you wish to study, and the required balance between computational efficiency and accuracy. For ReaxFF applications, several crucial considerations must guide your selection process to ensure meaningful and transferable results.

Elemental Composition and Compatibility

The most fundamental consideration in force field selection is ensuring coverage of all elements in your chemical system. ReaxFF parameters are typically developed for specific element sets, and using a force field that doesn't include all relevant elements can produce unrealistic results. Currently, two major branches of ReaxFF parameter sets exist: the combustion branch and the aqueous branch. The primary difference between these branches lies in their O/H parameters, with the combustion branch optimized for gas-phase water molecules and the aqueous branch targeted at aqueous chemistry and solution-phase systems [12]. This distinction is crucial when studying processes involving water or hydration.

Table 1: ReaxFF Branches and Their Applications

Branch Focus Area Key Characteristics Example Force Fields
Combustion Gas-phase reactions, hydrocarbons, high-energy materials Optimized for water as gas-phase molecule CHO.ff, HE.ff, HCONSB.ff
Aqueous Solution chemistry, biological interfaces, electrochemistry Targeted at aqueous chemistry and hydration AuCSOH.ff, CuCl-H2O.ff, FeOCHCl.ff
Transferability and System-Specific Optimization

While ReaxFF offers broad transferability across different phases and chemical environments, its parameters are typically trained against specific training sets relevant to particular applications. This specialization means that a force field performing excellently in one domain may produce unsatisfactory results in another. For instance, the ReaxFF for H/C/O compounds developed for combustion chemistry may be inaccurate in describing the mechanical properties of graphite and diamond [18]. Therefore, it's essential to verify that your chosen force field has been validated for properties and systems similar to your research focus.

Recent advances in parameter optimization frameworks offer promising avenues for improving force field accuracy and transferability. Methods combining simulated annealing (SA) and particle swarm optimization (PSO) algorithms with concentrated attention mechanisms (CAM) have demonstrated faster and more accurate parameter optimization compared to traditional metaheuristic methods [18]. These approaches can be particularly valuable when existing force fields require refinement for specific systems or when developing entirely new parameter sets.

Research Context and Targeted Properties

Different research domains prioritize distinct material properties and processes, necessitating specialized force field parameterizations. For battery research, accurate description of ion diffusion and interfacial reactions is paramount, while combustion chemistry requires precise reaction barriers and bond dissociation energies. Biomaterials applications often demand accurate treatment of organic-inorganic interfaces and solvation effects. Understanding which properties were prioritized during a force field's development will guide appropriate selection.

Available ReaxFF Force Fields and Their Applications

The ReaxFF methodology has been parameterized for numerous chemical systems across various research domains. These parameterizations are continually refined and expanded to address new scientific challenges. Below, we summarize key ReaxFF force fields and their targeted applications to assist researchers in selecting appropriate parameters for their specific systems.

Table 2: Selected ReaxFF Force Fields and Their Applications

Force Field Elements Branch Primary Applications Key References
CHO.ff C, H, O Combustion Hydrocarbon oxidation Chenoweth et al., J. Phys. Chem. A 2008
HCONSB.ff H, C, O, N, S, B Combustion Soot formation, coal combustion Castro-Marcano et al., Combust. Flame 2012
AuCSOH.ff Au, C, S, O, H Water Gold surfaces, nanoparticles, glycine solvation Keith et al., Phys. Rev. B 2010
CuCl-H2O.ff Cu, Cl, H, O Water Aqueous chloride, copper chloride Rahaman et al., J. Phys. Chem. A 2010
FeOCHCl.ff Fe, O, C, H, Cl Water Iron-oxyhydroxide systems Aryanpour et al., J. Phys. Chem. A 2010
HE.ff C, H, O, N Combustion High-energy materials, RDX Zhang et al., J. Phys. Chem. B 2009
LiS.ff Li, S Specialized Lithium-sulfur batteries [Citation:1]

The CHO.ff force field has been extensively applied to hydrocarbon oxidation systems, providing insights into combustion processes and reaction mechanisms. Meanwhile, the HCONSB.ff parameterization extends this capability to more complex systems involving sulfur and boron, making it valuable for studying soot formation and coal combustion. For electrochemical applications, specialized force fields like LiS.ff enable the study of lithium diffusion in battery cathode materials, allowing researchers to compute diffusion coefficients and understand ion transport mechanisms [4].

In the domain of materials science and nanotechnology, force fields such as AuCSOH.ff facilitate investigations of metal surfaces, nanoparticles, and their interactions with organic molecules. These parameterizations have been instrumental in understanding catalytic processes, material stability, and interface phenomena. Similarly, FeOCHCl.ff supports research on corrosion, mineralogy, and environmental chemistry by accurately describing iron-oxyhydroxide systems and their interactions with aqueous environments.

When a suitable force field doesn't exist for a particular system, researchers can request parameters from the ReaxFF development community or engage in parameter optimization projects. The van Duin group at Penn State University regularly collaborates with researchers worldwide to develop new parameter sets for emerging applications, with over 1,600 requests from six continents demonstrating the method's global impact [17].

Experimental Protocol: Calculating Diffusion Coefficients in Battery Materials

The calculation of diffusion coefficients represents a common application of ReaxFF in energy materials research, particularly for battery systems. This protocol outlines a detailed methodology for computing lithium-ion diffusion coefficients in cathode materials, based on established tutorials and publications [4] [19]. The workflow encompasses system preparation, molecular dynamics simulation, and multiple analysis techniques for diffusion coefficient determination.

G Start Start: System Preparation CIF Import Crystal Structure (CIF file) Start->CIF Build Build Li0.4S System (Insert Li atoms) CIF->Build Relax Geometry Optimization with Lattice Relaxation Build->Relax Anneal Simulated Annealing (300K→1600K→300K) Relax->Anneal Equil Equilibration MD (10000 steps, 1600K) Anneal->Equil Prod Production MD (100000 steps, 1600K) Equil->Prod Analyze Trajectory Analysis Prod->Analyze MSD MSD Analysis Analyze->MSD Primary method VACF VACF Analysis Analyze->VACF Alternative method Extrap Arrhenius Extrapolation to Lower Temperatures MSD->Extrap VACF->Extrap End Diffusion Coefficient Result Extrap->End

Diagram 1: Workflow for calculating diffusion coefficients using ReaxFF molecular dynamics. The process involves system preparation through simulated annealing, production MD simulations, and multiple analysis pathways.

System Preparation and Equilibration

Step 1: Import Crystal Structure

  • Begin by importing your cathode material's crystal structure from a CIF file into your molecular dynamics simulation package (e.g., AMSinput)
  • For lithium-sulfur systems, the alpha sulfur crystal structure serves as an appropriate starting point [4]

Step 2: Generate Lithiated System

  • Use builder functionality to insert lithium atoms into the crystal structure
  • For Li~0.4~S, insert 51 Li-atoms into the sulfur system using SMILES code [Li]
  • Alternatively, employ Grand Canonical Monte Carlo (GCMC) for more accurate lithiation [4]

Step 3: Geometry Optimization with Lattice Relaxation

  • Perform geometry optimization including lattice relaxation using an appropriate force field (e.g., LiS.ff)
  • Set task to "Geometry Optimization" and enable "Optimize lattice" option
  • Monitor the cell volume increase (e.g., from 3300 ų to 4400 ų for Li~0.4~S) as an indicator of successful relaxation [4]

Step 4: Create Amorphous Structure via Simulated Annealing

  • Set up a molecular dynamics simulation with 30000 steps
  • Configure temperature profile:
    • 0-5000 steps: Constant at 300 K
    • 5000-25000 steps: Heating from 300 K to 1600 K
    • 25000-30000 steps: Cooling from 1600 K to 300 K
  • Use Berendsen thermostat with damping constant of 100 fs
  • This annealing process creates amorphous structures relevant for battery materials [4]
Production Simulation and Analysis

Step 5: Set Up Production MD Simulation

  • Configure molecular dynamics simulation at target temperature (e.g., 1600 K)
  • Use 10000 equilibration steps followed by 100000 production steps
  • Set sample frequency to 5 (writing positions and velocities every 5 steps)
  • Use Berendsen thermostat at target temperature with damping constant of 100 fs [4]

Step 6: Calculate Diffusion Coefficient via Mean Squared Displacement (MSD)

  • After simulation completion, analyze trajectory using MSD analysis
  • Select appropriate time range (e.g., steps 2000-22001)
  • Set atoms to Li and max MSD frame to 5000 (corresponding to 6250 fs)
  • Generate MSD plot and determine diffusion coefficient using the relationship:

[ D = \frac{\text{slope(MSD)}}{6} ]

  • Verify linearity of MSD plot; non-linear regions indicate insufficient simulation length [4]

Step 7: Alternative Method - Velocity Autocorrelation Function (VACF)

  • As validation, compute diffusion coefficient through velocity autocorrelation function
  • Use same trajectory and select "Diffusion Coefficient (D)" property
  • Set atoms to Li and max ACF step to 5000
  • Determine D from the plateau region of the integral of VACF divided by 3:

[ D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t ]

  • Compare results with MSD method; values should be approximately equal [4]

Step 8: Extrapolate to Lower Temperatures Using Arrhenius Equation

  • To estimate diffusion coefficients at experimentally relevant temperatures (e.g., 300 K), perform simulations at multiple temperatures (600 K, 800 K, 1200 K, 1600 K)
  • Use Arrhenius relationship to determine activation energy and pre-exponential factor:

[ \ln{D(T)} = \ln{D0} - \frac{Ea}{k_{B}}\cdot\frac{1}{T} ]

  • Plot (\ln{(D(T))}) against (1/T) and perform linear fit to extract parameters
  • Extrapolate to lower temperatures using fitted Arrhenius equation [4]

Successful implementation of ReaxFF simulations requires both specialized software tools and carefully prepared chemical systems. The following table outlines key components of the computational researcher's toolkit for force field applications and diffusion coefficient calculations.

Table 3: Essential Research Reagents and Computational Resources

Resource Type Function/Purpose Example Sources/References
LiS.ff Force Field Parameters Describes Li-S interactions for battery simulations [4]
CHO.ff Force Field Parameters Models hydrocarbon oxidation for combustion studies [12]
AMS/ReaxFF Software Package Molecular dynamics simulation with ReaxFF implementation SCM (www.scm.com)
LAMMPS Software Package Open-source MD code with ReaxFF support Plimpton, J. Comp. Phys. (1995)
PuReMD Software Package Purdue Reactive Molecular Dynamics code [2]
CIF Files Structural Data Initial crystal structures for simulation setup [4]
DFT Reference Data Training Data Quantum mechanical data for force field validation [18] [2]

Specialized software packages form the foundation of ReaxFF simulations. The AMS/ReaxFF platform provides a user-friendly interface with dedicated tools for ReaxFF simulations, including built-in analysis capabilities for diffusion coefficients [4]. Alternatively, LAMMPS offers open-source molecular dynamics capabilities with ReaxFF integration, while PuReMD is specifically optimized for reactive force field simulations [2]. These packages enable researchers to set up, run, and analyze complex reactive simulations across diverse chemical systems.

Force field parameters represent the essential "reagents" in molecular simulations, determining the accuracy and applicability of the calculations. Parameters such as LiS.ff for lithium-sulfur battery systems or CHO.ff for combustion chemistry encode the specific interactions between elements [4] [12]. These parameter sets are typically developed through careful optimization against quantum mechanical reference data and experimental measurements when available. Researchers can obtain specialized force field parameters by requesting them from development groups or through collaborative projects [17].

Initial structural files in CIF format provide the starting configurations for simulations, while DFT reference data serves as the gold standard for force field validation and development [18] [2]. The availability of high-quality training data covering relevant chemical spaces is crucial for developing accurate and transferable force fields. Recent advances in parameter optimization frameworks that combine simulated annealing and particle swarm optimization algorithms have shown promising improvements in both the efficiency and accuracy of force field development [18].

The selection of appropriate force fields represents a critical step in molecular simulations that significantly influences the reliability and interpretability of computational results. For reactive systems requiring dynamic bond formation and cleavage, ReaxFF provides a powerful framework that balances computational efficiency with chemical accuracy. The methodology outlined in this application note—from force field selection to specialized protocols for diffusion coefficient calculation—offers researchers a structured approach for implementing ReaxFF in their investigations of complex chemical processes.

Future developments in ReaxFF methodology continue to expand its capabilities and applications. Ongoing research focuses on improving parameter optimization through advanced algorithms, enhancing transferability across broader chemical spaces, and integrating ReaxFF with other simulation techniques such as computational fluid dynamics [18] [17]. These advances will further establish ReaxFF as an indispensable tool in the computational researcher's toolkit, enabling increasingly accurate simulations of complex materials and processes across chemistry, materials science, and biological applications.

Step-by-Step Workflow: Calculating Diffusion Coefficients in Li-ion Battery Materials

The initial construction of a realistic atomistic model is a critical first step in molecular dynamics (MD) simulations of complex materials, such as those found in lithium-ion batteries. This application note details the protocols for building a Li~0.4~S cathode system, as used in ReaxFF MD simulations to compute lithium-ion diffusion coefficients. The procedures outlined herein—importing a crystal structure, manipulating it by inserting particles, and performing essential equilibration—form the foundation for subsequent simulated annealing and production MD runs. This framework is inspired by and adapted from established computational studies on lithiated sulfur cathode materials [4].

Research Reagent Solutions

The following table lists the essential computational "reagents" and their functions required to perform the system-building procedure.

Table 1: Essential Research Reagent Solutions and Software

Item Name Function/Description Critical Notes
AMSinput Graphical user interface for setting up calculations in the Amsterdam Modeling Suite [4]. Used for all steps: importing coordinates, structure manipulation, and setting calculation parameters.
ReaxFF Force Field Reactive force field to describe atomic interactions; enables modeling of bond formation and breaking [5] [2]. The LiS.ff parameter file is used for geometry optimization and MD simulations [4].
Crystal Structure File Initial atomic configuration of the system. Typically a Crystallographic Information File (.cif) for crystal structures like Sulfur(α) [4].
Builder Tool Integrated utility within AMSinput for inserting molecules or atoms into an existing structure [4]. Used to randomly insert Lithium atoms into the Sulfur crystal framework.

Protocol: System Generation and Equilibration

This section provides the detailed methodology for constructing and initially relaxing the Li~0.4~S system.

Importing the Sulfur(α) Crystal Structure

Objective: To load the initial crystal structure of the cathode material.

  • Open a new AMSinput window.
  • Select the ReaxFF engine.
  • Import the crystal structure: File → Import Coordinates.
  • In the file dialog, select and open the downloaded CIF file for the Sulfur(α) crystal [4].

Generating the Li~0.4~S System by Inserting Lithium Particles

Objective: To create the lithiated cathode material by randomly inserting Lithium atoms into the crystal lattice.

  • Access the Builder: In AMSinput, navigate to Edit → Builder.
  • Configure the insertion:
    • Tick the checkbox for Use number of molecules.
    • In the SMILES or xyz-file field, enter [Li] (the SMILES code for a single Lithium atom).
    • Set N mols to 51 to achieve the desired Li~0.4~S stoichiometry.
  • Execute the insertion: Click Generate Molecules. The Li atoms will be randomly placed into the simulation box.
  • Close the Builder window once the operation is complete [4].

Equilibrating the System via Geometry Optimization

Objective: To relax the newly constructed, high-energy structure to a stable local minimum and allow the unit cell to adjust.

  • Set the calculation task: In the main AMSinput panel, select Task → Geometry Optimization.
  • Select the force field: Click the folder icon next to Force Field and select the LiS.ff file.
  • Enable lattice optimization:
    • Go to Details → Geometry Optimization.
    • Tick the Optimize lattice checkbox. This is crucial for allowing the cell volume to change in response to the inserted atoms.
  • Run the calculation:
    • Save the project (File → Save As…).
    • Start the calculation (File → Run).
    • When prompted, click Yes to update the AMSinput structure with the optimized geometry [4].

Results and Validation

The successful execution of the geometry optimization yields a stable, pre-equilibrated Li~0.4~S structure ready for further processing. The primary quantitative metric for validation is the change in the unit cell volume.

Table 2: Key Results from System Geometry Optimization

System Property Pre-Optimization Post-Optimization Notes
Unit Cell Volume ~3300 ų ~4400 ų A significant volume expansion is expected and confirms the lattice has relaxed to accommodate the inserted Li ions [4].
System Energy High (initial, unphysical state) Lower, converged energy Indicates the structure has reached a local minimum on the potential energy surface.

Visualization: The relaxation process can be visualized using AMSmovie (SCM → Movie). Plotting the cell volume versus the optimization step provides a clear trajectory of the lattice expansion [4].

Workflow Diagram

The entire system-building and equilibration process is summarized in the following workflow.

Start Start: New AMSinput Project A Import Sulfur(α) CIF file Start->A B Insert 51 Li atoms using Builder tool A->B C Setup Geometry Optimization B->C D Select ReaxFF Force Field (LiS.ff) C->D E Enable Lattice Optimization D->E F Run Calculation E->F G Update Structure with Results F->G End Equilibrated Li₀.₄S System G->End

System Setup Workflow: This diagram outlines the key steps for importing a crystal structure, inserting lithium particles, and equilibrating the system via geometry optimization to create a stable Li~0.4~S model for subsequent molecular dynamics simulations.

Advanced System Creation via Simulated Annealing

For many applications, transforming the crystalline system into an amorphous structure may be necessary to better represent real-world conditions.

Objective: To create an amorphous Li~0.4~S structure by melting and rapidly quenching the system.

  • Set Up Molecular Dynamics: In AMSinput, change the task to Task → Molecular Dynamics. Set the number of steps to 30000.
  • Define the Annealing Temperature Profile: Configure the thermostat (e.g., Berendsen) with the following non-equilibrium profile [4]:
    • Step 0 - 5,000: Hold at 300 K.
    • Step 5,000 - 25,000: Ramp temperature from 300 K to 1600 K.
    • Step 25,000 - 30,000: Ramp temperature from 1600 K back to 300 K.
  • Run and Relax: Execute the simulated annealing calculation, then perform a final geometry optimization (with lattice optimization) on the resulting amorphous structure to ensure its stability [4].

Concluding Remarks

The protocols described provide a robust and reproducible method for generating atomistic models of complex battery materials. The correct implementation of these initial steps—importing the crystal, inserting ions, and carefully equilibrating the system—is paramount for the reliability of subsequent molecular dynamics simulations, particularly for the accurate calculation of properties like lithium-ion diffusion coefficients. The resulting equilibrated structure serves as the direct input for the production MD simulations detailed in the subsequent phase of the tutorial on diffusion coefficient calculation [4].

Creating Amorphous Structures via Simulated Annealing Protocols

The synthesis of amorphous materials, characterized by their lack of long-range periodic order, presents significant challenges due to the ultra-long relaxation times associated with glass transitions [20]. Simulated annealing, a computational technique implemented within molecular dynamics (MD) frameworks, has emerged as a powerful protocol for generating realistic atomic models of these disordered systems by mimicking the thermal processes of heating and rapid cooling [4]. This method is particularly valuable for creating amorphous structures for battery materials, protective coatings, and catalytic applications where disorder confers advantageous properties [4] [21].

When performed using the ReaxFF force field, simulated annealing enables the simulation of dynamic bond formation and breaking during the amorphization process, providing atomistic insights into material properties such as ionic diffusion in battery electrodes [4] [21]. This application note details comprehensive protocols for constructing amorphous materials via simulated annealing, with specific application to Liâ‚€.â‚„S cathode materials, and outlines subsequent procedures for calculating diffusion coefficients critical for understanding material performance [4].

Theoretical Background

Amorphous Materials and Their Characterization

Amorphous materials exhibit unique properties distinct from their crystalline counterparts, including isotropic atomic environments, abundant surface dangling bonds, and highly-unsaturated coordination sites [22]. These characteristics enable diverse applications in electronic devices, energy storage, and photoelectrocatalysis [22]. In the specific case of amorphous carbon, complexity arises from the simultaneous presence of sp, sp², and sp³ hybridizations, creating challenging topological disorders that can be characterized through radial distribution functions (RDF) and ring statistics [23].

The structural characterization of amorphous materials typically focuses on three key parameters: local bonding (deviations from crystalline symmetry), topological disorder (structural randomness and atomic density fluctuations), and chemical composition (elemental species and proportions) [22]. These descriptors can be quantified experimentally through techniques including scanning transmission electron microscopy (STEM), X-ray absorption spectroscopy (XAS), and Raman spectroscopy [22], or computationally through molecular dynamics simulations [4].

Simulated Annealing Fundamentals

Simulated annealing computationally mimics thermal annealing processes by first elevating a system temperature to eliminate memory of the initial configuration, followed by controlled cooling to promote the formation of a metastable amorphous structure [4]. This method effectively overcomes energy barriers between different molecular configurations, allowing the system to settle into a disordered state that may not be accessible through conventional equilibrium molecular dynamics [4] [20].

The ReaxFF force field is particularly suited for these simulations due to its bond-order formalism that enables dynamic bond formation and breaking during the annealing process, providing more accurate modeling of chemical reactivity during amorphous structure formation [21]. This approach has been successfully applied to various material systems, including lithiated sulfur cathode materials [4] and ruthenium-hydrogen systems [21].

Experimental Protocols

System Preparation and Equilibration

Initial Structure Import and Modification

  • Begin by importing a crystalline structure file (CIF format) into the molecular dynamics environment [4].
  • For Liâ‚€.â‚„S systems, insert lithium atoms randomly into the sulfur matrix using the builder functionality with SMILES code [Li] to specify single lithium atoms [4].
  • Perform initial geometry optimization with lattice relaxation to equilibrate the system using an appropriate force field (e.g., LiS.ff for lithiated sulfur) [4].

Force Field Parametrization for ReaxFF

  • Develop ReaxFF parameters through Monte Carlo global optimization that minimizes the difference between reference quantum-mechanical calculations and ReaxFF-computed properties [21].
  • Construct a comprehensive training set including equations of state for multiple crystal structures, surface formation energies, adsorption energies, and bond length scans [21].
  • Validate the force field by comparing radial distribution functions and energy-volume curves against density functional theory (DFT) calculations to ensure accuracy [21].
Simulated Annealing Procedure

Temperature Profile Configuration

  • Implement a multi-stage temperature profile within the molecular dynamics simulator [4]:
    • Stage 1 (Equilibration): Maintain system at constant temperature (300 K) for initial 5,000 steps [4].
    • Stage 2 (Heating): Linearly increase temperature from 300 K to the target annealing temperature (1600 K for Liâ‚€.â‚„S) over 20,000 steps [4].
    • Stage 3 (Quenching): Rapidly cool the system from the high annealing temperature back to 300 K over 5,000 steps [4].
  • Utilize a Berendsen thermostat with a damping constant of 100 fs throughout the simulation [4].
  • Employ a velocity Verlet integrator with a time step of 0.25 fs to maintain numerical stability [4].

Structural Relaxation

  • Following the simulated annealing procedure, perform a final geometry optimization with lattice relaxation to obtain the stable amorphous configuration [4].
  • Verify the amorphous structure through visual inspection and calculation of the radial distribution function, which should exhibit broad peaks indicative of short-range order without long-range periodicity [22] [4].

The following workflow illustrates the complete simulated annealing process for amorphous structure creation:

annealing_workflow Start Import Crystalline Structure (CIF Format) Modify Insert Dopant Atoms (Random or GCMC) Start->Modify Equilibrate Initial Geometry Optimization Modify->Equilibrate Anneal Simulated Annealing Equilibrate->Anneal Stage1 Stage 1: Constant T (300 K, 5000 steps) Anneal->Stage1 Stage2 Stage 2: Heating (300K to 1600K, 20000 steps) Stage1->Stage2 Stage3 Stage 3: Quenching (1600K to 300K, 5000 steps) Stage2->Stage3 Relax Final Geometry Optimization Stage3->Relax Analyze Structural Analysis (RDF, Ring Statistics) Relax->Analyze MD Production MD for Property Calculation Analyze->MD

Simulated Annealing Workflow for Amorphous Materials
Diffusion Coefficient Calculation

Production Molecular Dynamics Simulation

  • Configure an NVT ensemble molecular dynamics simulation with a target temperature (e.g., 1600 K for Liâ‚€.â‚„S) [4].
  • Set the simulation to 110,000 total steps, with 10,000 steps for equilibration and 100,000 steps for production data collection [4].
  • Use a sample frequency of 5 steps (writing atomic positions and velocities every 1.25 fs) to ensure adequate trajectory resolution [4].

Mean Squared Displacement Analysis

  • Calculate the mean squared displacement (MSD) of mobile ions (e.g., Li⁺) using the Einstein-Smoluchowski relation [4] [21]: MSD(t) = ⟨[r(0) - r(t)]²⟩
  • Compute the diffusion coefficient from the slope of the MSD versus time plot: D = slope(MSD)/6 for three-dimensional systems [4].
  • Ensure sufficient simulation length to obtain a linear MSD profile, indicating normal diffusion behavior [4].

Velocity Autocorrelation Function Method

  • As an alternative approach, calculate the velocity autocorrelation function (VACF) from the production trajectory [4].
  • Integrate the VACF over time to obtain the diffusion coefficient: D = (1/3) ∫⟨v(0)·v(t)⟩dt [4].
  • Validate results by comparing MSD and VACF methods, which should yield similar diffusion coefficients [4].

Temperature Extrapolation

  • Determine diffusion coefficients at multiple elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) [4].
  • Fit the temperature-dependent diffusion data to the Arrhenius equation: D(T) = Dâ‚€ exp(-Eₐ/kBT) [4].
  • Extract the pre-exponential factor (Dâ‚€) and activation energy (Eₐ) to enable extrapolation to lower temperatures relevant to experimental conditions [4].

Research Reagent Solutions

Table 1: Essential Computational Tools for ReaxFF Simulated Annealing

Research Reagent Function Application Example
ReaxFF Force Field Describes bond formation/breaking during MD simulations LiS.ff for lithiated sulfur systems [4]
Berendsen Thermostat Controls system temperature during annealing Maintaining temperature profile during simulated annealing [4]
Velocity Verlet Integrator Numerical integration of equations of motion Time evolution of atomic positions with 0.25 fs steps [4] [21]
Monte Carlo Global Optimization Parameter optimization for force field development Fitting ReaxFF parameters to DFT training data [21]
Radial Distribution Function (RDF) Characterizes short- and medium-range order in amorphous structures Quantifying structural disorder in amorphous carbon [22] [23]

Data Analysis and Interpretation

Structural Characterization

Radial Distribution Function Analysis

  • Calculate the radial distribution function (RDF) to quantify short-, medium-, and long-range order in the amorphous structure [22].
  • Compare RDF peaks between crystalline and amorphous configurations, with broader peaks indicating greater structural disorder [22] [23].
  • For amorphous carbon, analyze the relative proportions of sp² versus sp³ hybridization through integration of RDF peaks and coordination numbers [23].

Ring Statistics Assessment

  • Perform ring statistics to quantify topological disorder by identifying non-crystalline ring configurations (pentagons, hexagons, heptagons, etc.) [22].
  • Calculate the relative abundance of different ring sizes, with higher proportions of non-hexagonal rings indicating greater amorphous character [22].
  • For amorphous carbon synthesized at different temperatures, observe the transition from predominantly hexagonal rings (86% at 300°C) to more diverse ring configurations (28% 5/7/8-membered rings at 400°C) [22].
Diffusion Mechanism Analysis

Table 2: Diffusion Coefficient Calculation Methods

Method Formula Advantages Limitations
Mean Squared Displacement (MSD) D = slope(MSD)/6 Direct method, intuitive physical interpretation Requires linear MSD region, long simulation times [4]
Velocity Autocorrelation Function (VACF) D = (1/3)∫⟨v(0)·v(t)⟩dt Provides insight into diffusion mechanisms Requires high sampling frequency, sensitive to statistics [4]
Arrhenius Extrapolation D(T) = D₀exp(-Eₐ/kBT) Enables prediction of low-temperature diffusion Assumes constant mechanism across temperatures [4]

Finite-Size Effects Consideration

  • Account for system size dependencies in diffusion coefficient calculations, as finite simulation cells artificially constrain long-range ionic motion [4].
  • Perform simulations with progressively larger supercells and extrapolate results to the "infinite supercell" limit for accurate diffusion coefficients [4].
  • Utilize systems containing at least 3,500 atoms to ensure isotropic mechanical response and representative diffusion behavior [24].

Advanced Applications and Methodologies

Machine Learning Potential Integration

Recent advances incorporate machine learning potentials to enhance the accuracy of amorphous structure simulations while maintaining computational efficiency [23] [24]. The neuroevolution potential (NEP) framework demonstrates particular promise for simulating amorphous carbon annealing processes, achieving root mean square errors of 46.82 meV·atom⁻¹ for energies and 561.32 meV·Å⁻¹ for forces compared to density functional theory references [23]. This approach enables large-scale molecular dynamics simulations with quantum-mechanical accuracy, essential for predicting mechanical properties and structural transformations in complex amorphous systems [24].

Data-Assimilation Enhanced Annealing

The integration of experimental data directly into the simulated annealing process through data-assimilation methodologies represents a cutting-edge advancement in amorphous structure modeling [20]. This approach augments the interatomic potential with penalty functions derived from experimental measurements, generating atomic models that simultaneously satisfy energetic stability criteria and experimental constraints [20]. Particularly valuable for interpreting incomplete experimental data, this method has successfully generated more ordered amorphous ice structures at intermediate ranges as validated through persistent homology analysis [20].

Defect-Engineered Amorphous Materials

Simulated annealing protocols effectively model the role of microstructural defects in amorphous material performance. In ruthenium thin films, ReaxFF molecular dynamics simulations demonstrate how grain boundaries function as sinks and highways for hydrogen diffusion, significantly altering permeation behavior [21]. These simulations reveal that tilt and twist grain boundaries provide energetically favorable sites for hydrogen accumulation, blocking transverse transport while enhancing lateral diffusion along boundary planes [21]. Such insights enable defect engineering strategies to tailor material properties, such as designing Ru film morphologies that curtail hydrogen permeation in extreme ultraviolet lithography applications [21].

In ReaxFF molecular dynamics (MD) simulations, a meticulously designed protocol for equilibration and production sampling is crucial for obtaining statistically meaningful and chemically accurate results, particularly for properties like diffusion coefficients. The reactive nature of the force field, which calculates bond orders dynamically based on interatomic distances, necessitates careful system preparation to avoid unphysical reactions caused by initial strain or inappropriate starting configurations [25] [2]. A robust simulation strategy involves an initial equilibration phase to relieve internal stresses, followed by a production phase where parameters are optimized for efficient and accurate data collection. This protocol is especially critical within the context of thesis research on ion diffusion in battery materials, where reliable kinetics data is paramount.

Core ReaxFF Parameters for MD Simulations

The ReaxFF engine in the Amsterdam Modeling Suite (AMS) uses specific parameters that control the simulation of reactive systems. Understanding these is essential for both equilibration and production runs.

Table 1: Key ReaxFF Engine Parameters for MD Setup

Parameter Default Value Description & Relevance to Equilibration/Sampling
ForceField (None, required) Path to the force field file (e.g., CHO.ff). The choice of force field is foundational and must be appropriate for the chemical system [25].
BondDistanceCutoff 5.0 Ã… Maximum distance to search for bonds. A larger cutoff may be needed for systems with large atomic radii [25].
BondOrderCutoff 0.001 Minimum bond order for evaluating 3-/4-body potentials. Affects the detection of chemical interactions [25].
TaperBO No Enables tapered bond orders to remove energy discontinuities, improving energy conservation and geometry optimization convergence [25].
NonReactive No If set to Yes, bonds are determined only at the simulation's start. Highly recommended for the initial equilibration of unrelaxed systems to prevent unwanted reactions [25].

Charge Equilibration Settings

The Charges block controls the charge equilibration method, a critical part of the ReaxFF potential. For production MD, the settings should ensure a stable and efficient calculation of electrostatic interactions [25].

Protocol 1: Standard Equilibration for Reactive Systems

This protocol is designed to prepare a system with significant initial conformational strain without allowing uncontrolled chemical reactions.

  • Initial Energy Minimization: Begin with a geometry optimization (including lattice relaxation if periodic) to find a local energy minimum and relieve severe clashes [4].
  • Non-Reactive MD Equilibration: Run a short MD simulation (e.g., 10-50 ps) with the NonReactive Yes flag enabled. This allows the system to relax thermally and mechanically without forming or breaking bonds, protecting the initial bonding topology [25].
  • Thermalization Ramp: Gradually heat the system from a low temperature (e.g., 100 K) to the target production temperature using a thermostat like Berendsen or Nose-Hoover. This gentle ramp prevents temperature shock.
  • Isothermal Equilibration: Run an NVT simulation at the target temperature until key properties (temperature, pressure, total energy) stabilize around a steady average.
  • Density Equilibration (NPT): If studying a condensed phase, switch to an NPT ensemble to equilibrate the system density at the target temperature and pressure.
  • Reactive Preparation: For the final step of equilibration, disable the NonReactive flag and run a short reactive NVE or NVT simulation. This allows the system to find its natural, reactive bonding state before the production run.

Protocol 2: Simulated Annealing for Amorphous Systems

For generating amorphous structures, like the Li0.4S cathode material studied in the diffusion tutorial, a simulated annealing protocol is highly effective [4]. The workflow for this protocol is illustrated in the diagram below.

Start Start: Optimized Crystal Structure Step1 1. Initial Equilibration NVT, 300 K ~5,000 steps Start->Step1 Step2 2. Heating Phase NVT, 300 K → 1600 K ~20,000 steps Step1->Step2 Step3 3. Rapid Quench NVT, 1600 K → 300 K ~5,000 steps Step2->Step3 Step4 4. Final Relaxation Geometry Optimization (Lattice + Atoms) Step3->Step4 End End: Amorphous Structure for Production MD Step4->End

Production Sampling for Diffusion Coefficients

The production phase is dedicated to generating a trajectory for analysis. Key parameters must be set to ensure accurate calculation of mean-squared displacement (MSD) or velocity autocorrelation function (VACF).

Table 2: Production MD Parameters for Diffusion Analysis

Parameter Recommendation Rationale
Task Molecular Dynamics -
Ensemble NVT Maintains target temperature for kinetics studies.
Time Step 0.25 fs Standard for ReaxFF; necessary for stability during bond-breaking/forming events [26].
Total Steps 100,000 - 1,000,000+ Must be long enough for diffusive (linear MSD) regime to emerge.
Thermostat Berendsen or Nose-Hoover Berendsen (damping ~100 fs) is often sufficient [4].
Sample Frequency 5-20 steps Writes trajectory every 1.25-5.0 fs. Lower is needed for VACF; higher suffices for MSD, saving disk space [4].

Example Production Input Snippet:

Analysis: Calculating the Diffusion Coefficient

After running the production MD, the diffusion coefficient ( D ) can be calculated from the trajectory using two primary methods.

Mean Squared Displacement (MSD) Method

This is the most common and straightforward method. The MSD is calculated as: [ MSD(t) = \langle |\mathbf{r}(t) - \mathbf{r}(0)|^2 \rangle ] where ( \mathbf{r}(t) ) is the position of an ion at time ( t ), and the angle brackets denote an average over all ions and time origins. For normal diffusion, in three dimensions, the MSD is related to ( D ) by: [ MSD(t) = 6Dt + C ] Thus, ( D ) is obtained as one-sixth of the slope of the linear portion of the MSD versus time curve [4].

Practical Application:

  • In AMSmovie, select the relevant atoms (e.g., Li).
  • Choose a sufficiently long and linear regime of the MSD plot for the linear fit (e.g., from 2 ps to the end of the trajectory).
  • The tool will output ( D \approx \text{slope} / 6 ).

Velocity Autocorrelation Function (VACF) Method

The Green-Kubo relation relates ( D ) to the integral of the VACF: [ D = \frac{1}{3} \int_0^{\infty} \langle \mathbf{v}(0) \cdot \mathbf{v}(t) \rangle dt ] where ( \mathbf{v}(t) ) is the velocity at time ( t ) [4].

Practical Application:

  • This method requires high-frequency trajectory sampling (low SampleFrequency).
  • In AMSmovie, the "Autocorrelation function" analysis will compute and integrate the VACF automatically, directly yielding ( D ).

Extrapolation to Lower Temperatures

Due to the limited timescales of MD, calculating ( D ) at room temperature can be prohibitive. A common solution is to use the Arrhenius equation to extrapolate from higher temperatures [4]: [ D(T) = D0 \exp(-Ea / kB T) ] [ \ln D = \ln D0 - \frac{Ea}{kB} \frac{1}{T} ]

  • Calculate ( D ) at several elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K).
  • Plot ( \ln D ) versus ( 1/T ). The slope is ( -Ea/kB ), and the intercept is ( \ln D_0 ).
  • Use the fitted parameters to estimate ( D ) at your temperature of interest (e.g., 300 K).

The Scientist's Toolkit: Essential Research Reagent Solutions

Table 3: Key Computational Tools and Their Functions

Item Function in ReaxFF MD Simulations
AMS Driver/Engine The primary computational framework (SCM) that manages the simulation, including task execution (MD, optimization) and integration of the ReaxFF engine [27].
ReaxFF Force Field File (*.ff) The parameter set file containing all fitted terms (bond, angle, torsion, charge, etc.) that define the potential energy surface for a specific set of elements [25] [2].
AMSinput The graphical user interface (GUI) for setting up, configuring, and submitting ReaxFF calculations [27].
AMSmovie The primary tool for trajectory visualization and analysis, including calculation of MSD, VACF, diffusion coefficients, and other time-dependent properties [4].
LAMMPS/PuReMD Alternative, open-source MD engines that also implement the ReaxFF potential, offering high parallel efficiency for large systems [2] [26].
NonReactive Mode A crucial "reagent" for equilibration. It freezes the bonding topology, acting as a protective restraint to relax geometric strain without triggering chemical reactions [25].
Berendsen Thermostat A commonly used algorithm for temperature control during equilibration and production phases due to its simplicity and efficiency [4].
TripalmitoleinTripalmitolein, CAS:129784-33-4, MF:C51H92O6, MW:801.3 g/mol
4-Hydroxybenzamide4-Hydroxybenzamide, CAS:619-57-8, MF:C7H7NO2, MW:137.14 g/mol

In molecular dynamics (MD) simulations, the self-diffusion coefficient ((D)) is a critical parameter for quantifying atomic or ionic mobility within a material. The Mean Squared Displacement (MSD) method provides a direct and computationally efficient approach for calculating (D) from MD trajectories, making it the recommended technique for analyzing diffusion processes [4]. This method is particularly valuable in energy materials research, such as studying lithium-ion transport in battery electrodes and solid-electrolyte interphases (SEI) [8]. The MSD approach leverages the Einstein-Smoluchowski relation, which connects macroscopic diffusive behavior with microscopic atomic displacements observed in MD simulations [21]. This protocol details the application of the MSD method within ReaxFF MD simulations, providing a standardized framework for obtaining accurate diffusion coefficients relevant to battery material design and other energy storage applications.

Theoretical Foundation

The Mean Squared Displacement method derives from the statistical mechanics of random walks, where the diffusion coefficient is proportional to the slope of the mean squared displacement over time.

Mathematical Formalism

For a three-dimensional system, the self-diffusion coefficient is calculated using the Einstein relation:

[ MSD(t) = \langle | \mathbf{r}(t) - \mathbf{r}(0) |^2 \rangle ]

[ D = \frac{\text{slope}(MSD)}{6} ]

where (\mathbf{r}(t)) represents the position vector of a diffusing particle at time (t), and the angle brackets denote an ensemble average over all particles of the same type and time origins [4]. The factor of 6 accounts for the three spatial dimensions in the system (d=3), as the MSD increases as (2dDt) [21].

Key Assumptions and Considerations

The MSD method relies on several critical assumptions that must be satisfied for accurate results:

  • Fickian Diffusion Regime: The analysis assumes normal, Fickian diffusion where MSD increases linearly with time. This typically requires the simulation to be sufficiently long to capture this linear regime while avoiding initial ballistic motion and final finite-size effects.
  • Ergodicity: The system must be ergodic, meaning that the ensemble average is equivalent to the time average.
  • Finite-Size Effects: The simulated supercell must be large enough to minimize artificial correlation effects. For highly accurate results, simulations should be performed with progressively larger supercells with extrapolation to the "infinite supercell" limit [4].

Experimental Protocol

System Preparation and Equilibration

Objective: Prepare a stable, equilibrated system for production MD simulation.

  • Initial Structure Generation:

    • Import crystal structure from CIF file or use pre-equilibrated structures [4].
    • For complex systems like lithiated sulfur cathodes (Li(_{0.4})S), insert lithium atoms into the sulfur matrix using builder functionality or Grand Canonical Monte Carlo (GCMC) methods [4].
    • Perform geometry optimization with lattice relaxation using an appropriate ReaxFF force field (e.g., LiS.ff for Li-S systems).

  • System Equilibration:

    • Conduct simulated annealing for amorphous systems if needed [4]:
      • Heat from 300 K to target temperature (e.g., 1600 K) over 20000 steps
      • Rapidly cool back to 300 K over 5000 steps
      • Use Berendsen thermostat with damping constant of 100 fs
    • Perform final geometry optimization with lattice relaxation on the annealed structure.
    • Equilibrate the system at the target production temperature (e.g., 1600 K) for at least 10000 steps in the NVT ensemble using a Nosé-Hoover chain thermostat [4] [21].

Production Molecular Dynamics Simulation

Objective: Generate trajectory data for MSD analysis.

  • Simulation Parameters:

    • Task: Molecular Dynamics [4]
    • Ensemble: NVT (constant number of particles, volume, and temperature)
    • Thermostat: Berendsen or Nosé-Hoover chain [4] [21]
    • Temperature: Set to desired value (e.g., 1600 K for high-temperature studies)
    • Time step: 0.25 fs [21]
    • Total steps: Minimum 100,000-200,000 for reasonable statistics [4]
    • Sample frequency: 5-10 steps (writing atomic positions every 1.25-2.5 fs) [4]

  • Execution:

    • Run production MD simulation with specified parameters.
    • Monitor temperature, pressure, and energy stability throughout simulation.
    • Save trajectory file containing atomic positions and velocities for subsequent analysis.

MSD Analysis Procedure

Objective: Calculate diffusion coefficient from MD trajectory.

  • Trajectory Processing:

    • Load production trajectory into analysis software (e.g., AMSmovie, MDAnalysis) [4] [21].
    • Select appropriate atom type for analysis (e.g., Li atoms for lithium diffusion).
    • Exclude initial equilibration period from analysis (e.g., first 2000 steps).

  • MSD Calculation:

    • Set maximum MSD frame to appropriate value (e.g., 5000 frames, corresponding to 6250 fs with 1.25 fs between frames) [4].
    • Calculate MSD using multiple time origins for improved statistics.
    • Generate MSD versus time plot.

  • Linear Regression:

    • Identify linear region of MSD curve, excluding initial ballistic regime and final noisy region.
    • Perform linear fit on the MSD curve from the "Start Time Slope" to appropriate end point.
    • Extract slope of the linear fit.

  • Diffusion Coefficient Calculation:

    • Apply Einstein relation: (D = \frac{\text{slope}(MSD)}{6}) for 3D diffusion.
    • Report diffusion coefficient with appropriate units (typically m²/s or cm²/s).

Data Analysis and Interpretation

Quantitative Data Presentation

Table 1: Exemplary Lithium Diffusion Coefficients in Li(_{0.4})S at 1600K

Method Diffusion Coefficient (m²/s) Simulation Length Notes
MSD Analysis 3.09 × 10⁻⁸ 100,000 steps Linear region: 2000-22001 steps [4]
VACF Analysis 3.02 × 10⁻⁸ 100,000 steps Consistent with MSD approach [4]

Table 2: MSD Analysis Parameters for Different Systems

Parameter Li(_{0.4})S System [4] H in Ru System [21]
Time Step 0.25 fs 0.25 fs
Sample Frequency 5 steps 1000 steps
Production Steps 110,000 Varies by system
MSD Frame Limit 5000 Not specified
Thermostat Berendsen Nosé-Hoover Chain

Validation and Quality Control

  • Convergence Assessment:

    • Ensure MSD plot shows clear linear regime over significant time range.
    • Plot instantaneous diffusion coefficient (slope/6 calculated up to each time point); should converge to horizontal line [4].
    • If MSD curve is not linear, extend simulation time for better statistics.

  • Cross-Validation:

    • Compare with Velocity Autocorrelation Function (VACF) method when possible [4].
    • For Li(_{0.4})S at 1600K, MSD and VACF methods show excellent agreement (3.09 vs 3.02 × 10⁻⁸ m²/s) [4].

  • Error Analysis:

    • Calculate standard error from linear regression fit.
    • Perform block averaging to assess statistical uncertainty.
    • Consider running multiple independent simulations with different initial velocities.

Temperature Dependence and Extrapolation

For practical applications, diffusion coefficients at operating temperatures (e.g., 300K for batteries) can be estimated through Arrhenius extrapolation:

  • Multi-Temperature Simulations:

    • Perform MSD analysis at multiple temperatures (e.g., 600K, 800K, 1200K, 1600K) [4].
    • Calculate diffusion coefficient at each temperature.

  • Arrhenius Analysis:

    • Plot ln(D) versus 1/T.
    • Fit to Arrhenius equation: (D(T) = D0 \exp(-Ea / k_BT)).
    • Extract activation energy ((Ea)) and pre-exponential factor ((D0)).
    • Use fitted parameters to extrapolate D to lower temperatures [4].

G Start Start MD Simulation Prep System Preparation & Equilibration Start->Prep Prod Production MD Run Prep->Prod Traj Trajectory File Generation Prod->Traj MSDCalc MSD Calculation Traj->MSDCalc LinearFit Linear Regression on MSD Curve MSDCalc->LinearFit DCalc D = slope / 6 LinearFit->DCalc Validation Validation & Error Analysis DCalc->Validation Report Final Diffusion Coefficient Validation->Report

Figure 1: Workflow for calculating diffusion coefficients from Mean Squared Displacement in ReaxFF MD simulations.

The Scientist's Toolkit

Table 3: Essential Research Reagents and Computational Tools

Item Function/Description Example/Specification
ReaxFF Force Field Defines interatomic potentials for reactive MD simulations LiS.ff for Li-S systems [4]; Parameterized Ru/H force field for H diffusion in Ru [21]
MD Software Package Engine for performing molecular dynamics simulations AMS with ReaxFF module [4]; LAMMPS with ReaxFF implementation [2]
Trajectory Analysis Tools Software for analyzing MD trajectories and calculating MSD AMSmovie [4]; MDAnalysis Python package [21]
Visualization Software For monitoring simulation progress and structural analysis AMSmovie [4]; VMD; OVITO
Structure Builder Tools for creating initial molecular structures AMSinput Builder [4]; Grand Canonical Monte Carlo (GCMC)
SoretolideSoretolide, CAS:130403-08-6, MF:C13H14N2O2, MW:230.26 g/molChemical Reagent
1,3-Diolein1,3-Diolein, CAS:2465-32-9, MF:C39H72O5, MW:621.0 g/molChemical Reagent

Troubleshooting and Optimization

Common Issues and Solutions

  • Non-linear MSD:

    • Cause: Insufficient simulation time or poor equilibration.
    • Solution: Extend production simulation; verify proper equilibration through energy and temperature stability.

  • High Statistical Noise:

    • Cause: Inadequate sampling of diffusive species.
    • Solution: Increase number of diffusing atoms; extend simulation duration; use multiple time origins for averaging.

  • Finite-Size Effects:

    • Cause: Artificial correlation in small simulation cells.
    • Solution: Increase supercell size; perform simulations with progressively larger cells and extrapolate to infinite size [4].

Optimization Strategies

  • Computational Efficiency:

    • Adjust sample frequency based on analysis needs (higher values for MSD, lower for VACF) [4].
    • Use appropriate time step (0.25 fs for ReaxFF) [21].
    • Balance system size with simulation length based on research question.

  • Accuracy Improvements:

    • For absolute diffusion coefficients, perform finite-size extrapolation.
    • Use multiple independent trajectories with different initial conditions.
    • Validate against alternative methods (VACF) when possible [4].

Applications and Significance

The MSD method for calculating diffusion coefficients has broad applications in materials science and energy research:

  • Battery Materials Development:

    • Screening electrode materials for high ionic conductivity [4] [8].
    • Studying Li-ion transport through solid-electrolyte interphases (SEI) [8].

  • Hydrogen Storage and Permeation:

    • Investigating H diffusion through metal thin films and grain boundaries [21].

  • Catalysis and Combustion:

    • Analyzing species transport in catalytic systems and combustion processes [28].

The protocol described herein provides a standardized approach for obtaining reliable diffusion coefficients from ReaxFF MD simulations, enabling quantitative comparison of atomic mobility across different material systems and contributing to the accelerated design of advanced materials for energy applications.

Within the broader scope of ReaxFF molecular dynamics (MD) tutorials for determining diffusion coefficients, the Velocity Autocorrelation Function (VACF) method provides a powerful alternative to the more common Mean Squared Displacement (MSD) approach. The diffusion coefficient is a critical parameter for understanding mass transport in materials, influencing properties like ionic conductivity in battery electrodes [4] and water permeability in polymers [29]. This application note details the theoretical foundation, practical computational protocols, and analysis techniques for calculating diffusion coefficients via VACF using ReaxFF MD simulations, providing researchers with a robust framework for investigating dynamic processes in complex systems.

Theoretical Foundation

The Velocity Autocorrelation Function measures how a particle's velocity correlates with itself over time, offering fundamental insights into dynamical processes and local environment effects. The VACF is defined mathematically as:

[ \text{VACF}(t) = \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle ]

where (\textbf{v}(0)) and (\textbf{v}(t)) represent the velocity vectors of a particle at time zero and time (t), respectively, and the angle brackets denote an average over all particles and time origins [30].

The diffusion coefficient (D) is obtained from the time integral of the VACF through the Green-Kubo relation:

[ D = \frac{1}{3} \int{0}^{t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle dt ]

This integral represents the total area under the VACF curve, which directly relates to the particle's mobility [4]. Unlike the MSD method, which requires particle displacements to reach the diffusive regime, the VACF approach captures short-time dynamics and can provide insights into local interactions and confinement effects. The VACF typically decays rapidly from its initial value, often exhibiting negative regions that indicate "cage effects" where particles are temporarily trapped by their neighbors before the correlations ultimately vanish at longer times.

Computational Setup and Parameters

Proper MD simulation setup is crucial for obtaining reliable diffusion coefficients from VACF analysis. The following parameters have been optimized for ReaxFF simulations of various systems, including lithium-ion battery materials and organic plasticizers.

Table 1: Key Parameters for ReaxFF MD Simulations for VACF Analysis

Parameter Category Specific Parameters Recommended Values Purpose and Rationale
Force Field Selection ReaxFF Force Field System-specific (e.g., LiS.ff for Li-S systems [4], Water2017.ff for aqueous systems [30]) Provides reactive potential for bond formation/breaking during MD
MD Engine Settings Task Molecular Dynamics [4] Specifies molecular dynamics as the calculation type
Time Step 0.25-0.5 fs [4] [30] Balances computational efficiency with numerical stability
Number of Steps 100,000-200,000 [4] [30] Ensures sufficient trajectory length for statistical averaging
Trajectory Sampling Sampling Frequency 1-5 steps [4] Determines interval for saving atomic positions and velocities
Total Sampled Frames 20,000-40,000 [4] Provides adequate data points for VACF calculation
Thermostat Settings Thermostat Type Berendsen [4] Maintains constant temperature during production run
Temperature System-dependent (e.g., 1600K for Liâ‚€.â‚„S [4], 298K/338K for plasticizers [29]) Controls thermal energy of the system
Damping Constant 100 fs [4] Determines coupling strength to thermal bath

Step-by-Step Protocol

System Preparation and Equilibration

  • Initial Structure Generation: Begin with a properly equilibrated system. For battery materials like Liâ‚€.â‚„S, this may involve importing crystal structures from CIF files, inserting lithium atoms using builder tools or Grand Canonical Monte Carlo (GCMC), and performing geometry optimization with lattice relaxation [4].

  • Amorphous Structure Creation (if needed): For amorphous systems like Liâ‚€.â‚„S, employ simulated annealing through MD with a specific temperature profile: maintain at 300K for 5000 steps, heat from 300K to 1600K over 20000 steps, then rapidly cool to 300K over 5000 steps [4].

  • System Equilibration: Perform a final geometry optimization including lattice relaxation to ensure the system is at a local energy minimum before production MD [4].

Production MD Simulation

  • Parameter Configuration: Set up the MD calculation with the parameters outlined in Table 1. For VACF analysis, a higher sampling frequency (e.g., every 1-5 steps) is crucial as it captures the rapid velocity fluctuations [4].

  • Thermostat Setup: Configure the Berendsen thermostat with the target temperature for diffusion measurement and a damping constant of 100 fs. Clear any duration fields to maintain constant temperature throughout the simulation [4].

  • Simulation Execution: Run the production MD simulation with sufficient steps (typically 100,000-200,000) to gather adequate statistics. For the Liâ‚€.â‚„S system at 1600K, 110,000 total steps with 10,000 equilibration steps followed by 100,000 production steps has been used successfully [4].

VACF Calculation and Diffusion Coefficient Determination

  • Trajectory Processing: After completing the MD simulation, extract the velocity trajectory from the results. The time between velocity frames is determined by (\Delta t = \text{samplefrequency} \times \text{timestep}) (e.g., (5 \times 0.25 \text{ fs} = 1.25 \text{ fs})) [4].

  • VACF Computation: Calculate the velocity autocorrelation function using the get_velocity_acf function available in the AMSResults API [30]:

  • Diffusion Coefficient Calculation: Compute the diffusion coefficient by integrating the VACF using the get_diffusion_coefficient_from_velocity_acf function [30]:

  • Convergence Verification: Plot the integrated VACF (D(t) curve) and verify that it plateaus to a constant value at long times. A horizontal asymptote indicates proper convergence, while a non-converged curve suggests the need for a longer simulation [4].

The following diagram illustrates the complete workflow from MD simulation to diffusion coefficient calculation:

MDSetup Set up Production MD Simulation MDRun Run ReaxFF MD Simulation MDSetup->MDRun ExtractVel Extract Velocity Trajectory MDRun->ExtractVel ComputeVACF Compute VACF ExtractVel->ComputeVACF Integrate Integrate VACF for D ComputeVACF->Integrate CheckConv Check Convergence Integrate->CheckConv CheckConv->MDRun Not Converged Result Report Diffusion Coefficient CheckConv->Result Converged

Data Analysis and Interpretation

VACF and Diffusion Coefficient Curves

Proper analysis of VACF and its integral is essential for obtaining accurate diffusion coefficients. The following characteristics should be observed in well-converged calculations:

  • VACF Decay: The VACF should decay rapidly from its initial value, often exhibiting negative regions that reflect the "caging" of particles by their neighbors before eventually vanishing at long times due to loss of correlation [30].

  • D(t) Convergence: The integrated VACF (D(t) curve) should reach a clear plateau, forming a horizontal asymptote at long times. The value of this plateau is the diffusion coefficient. If the curve continues to increase or decrease without leveling off, the simulation length is insufficient [4].

Comparison with MSD Method

The VACF method provides an important validation approach when compared with the more commonly used MSD technique:

Table 2: Comparison of VACF and MSD Methods for Diffusion Coefficient Calculation

Aspect VACF Method MSD Method
Fundamental Relation ( D = \frac{1}{3} \int{0}^{t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle dt ) [4] ( D = \frac{\text{slope}(MSD)}{6} ), ( MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ) [4]
Sampling Requirements Requires higher sampling frequency (every 1-5 steps) to capture velocity correlations [4] Can use lower sampling frequency (saves disk space) [4]
Convergence Indicator Plateau in the time-dependent diffusion coefficient curve [4] Linear regime in MSD vs. time plot [4]
Computational Advantages More efficient for confined systems or complex local environments [29] More intuitive and directly related to particle displacements
Reported Values D = 3.02 × 10⁻⁸ m² s⁻¹ for Li in Li₀.₄S at 1600K [4] D = 3.09 × 10⁻⁸ m² s⁻¹ for Li in Li₀.₄S at 1600K [4]

As shown in Table 2, both methods should yield comparable diffusion coefficients when properly applied, as demonstrated in the Li₀.₄S system where VACF and MSD methods gave values of 3.02 × 10⁻⁸ m² s⁻¹ and 3.09 × 10⁻⁸ m² s⁻¹, respectively [4].

Research Reagent Solutions

The following table outlines essential computational tools and their functions for implementing VACF analysis in ReaxFF MD simulations:

Table 3: Essential Computational Tools for VACF Analysis

Tool Name Type/Function Specific Application in VACF Analysis
AMS Package MD Simulation Engine Performs ReaxFF molecular dynamics simulations with trajectory output [4] [30]
PLAMS Python Scripting Library Provides automation and analysis tools for high-throughput calculations [30]
AMSmovie Visualization & Analysis Generates VACF plots and calculates diffusion coefficients through GUI [4]
ReaxFF Force Fields Parameter Sets System-specific force fields (e.g., LiS.ff, Water2017.ff) for accurate dynamics [4] [30]
getvelocityacf() Analysis Function Calculates velocity autocorrelation function from MD trajectory [30]
getdiffusioncoefficientfromvelocity_acf() Analysis Function Computes diffusion coefficient via integration of VACF [30]

Troubleshooting and Optimization

Common Issues and Solutions

  • Non-Converged D(t) Curve: If the integrated VACF does not reach a clear plateau, extend the simulation length. For the Liâ‚€.â‚„S system, 100,000 production steps at 1600K was sufficient [4].

  • Poor Statistics: Increase the number of atoms in the simulation box or run multiple independent simulations with different initial velocities to improve averaging.

  • Finite-Size Effects: The diffusion coefficient depends on supercell size unless the supercell is very large. Perform simulations for progressively larger supercells and extrapolate to the "infinite supercell" limit [4].

Temperature Dependence and Extrapolation

Calculating diffusion coefficients at low temperatures (e.g., 300K) may require prohibitively long simulations to observe sufficient diffusion events. A practical solution involves:

  • Performing simulations at multiple elevated temperatures (e.g., 600K, 800K, 1200K, 1600K)
  • Fitting the results to the Arrhenius equation: ( D(T) = D0 \exp{(-Ea / k_{B}T)} )
  • Extrapolating to lower temperatures using the obtained activation energy (Ea) and pre-exponential factor (D0) [4]

This approach has been successfully applied in studies of water diffusion in plasticizers at both 298K and 338K [29], as well as in Liâ‚€.â‚„S battery materials [4].

Application Notes

The VACF method for diffusion coefficient calculation has been successfully applied across diverse research domains:

  • Battery Materials: Investigating lithium-ion diffusion in Liâ‚€.â‚„S cathode materials for understanding and improving battery performance [4].

  • Polymer Systems: Studying water diffusion in plasticizers like 2,4-DNEB and 2,4,6-TNEB, which is crucial for understanding stability of nitrocellulose-based propellants and binders [29].

  • Aqueous Solutions: Analyzing ion-water interactions and their effects on water dynamics in electrolyte solutions, providing insights into solvation structures and transport properties [31].

The VACF method is particularly valuable when studying systems with complex local environments or confined geometries where the MSD approach may be challenging to apply due to non-diffusive regimes in the available simulation time scales.

This application note provides a detailed protocol for calculating the lithium-ion diffusion coefficient in a Liâ‚€.â‚„S cathode material using ReaxFF molecular dynamics (MD) simulations. The content is framed within broader thesis research on ReaxFF molecular dynamics diffusion coefficient tutorials, offering a practical case study for researchers investigating lithium-sulfur battery systems. The methodology presented enables the determination of transport properties critical for evaluating cathode material performance, focusing specifically on the computation of diffusion coefficients through mean-squared displacement (MSD) and velocity autocorrelation function (VACF) analyses [4]. The protocols outlined are adapted from established computational workflows originally described in research on lithiated sulfur cathode materials [4], providing a robust framework for studying ionic diffusion in battery materials using reactive force fields.

Experimental Setup and Computational Methodology

Research Reagent Solutions and Essential Materials

The computational experiments require specific software tools and parameters as detailed in the table below.

Table 1: Research Reagent Solutions for ReaxFF MD Simulations

Item Name Function/Purpose Specifications/Details
ReaxFF Force Field Defines interatomic interactions for Li-S systems LiS.ff parameter file; specifically parameterized for Li-S interactions [4]
Initial Structure Provides starting atomic configuration Liâ‚€.â‚„S structure (e.g., Li04S_amorphous.xyz) [4]
MD Engine Performs molecular dynamics simulations AMS software with ReaxFF module [4] or QuantumATK with ATK-ForceField [32]
Structure Visualization Visualizes trajectories and analysis results AMSmovie tool [4]
Thermostat Algorithm Controls temperature during MD simulations Berendsen thermostat [4]

System Preparation and Equilibration Protocol

Initial Structure Generation

The Li₀.₄S system can be prepared through two primary approaches. For crystalline systems, begin by importing a sulfur (α) crystal structure from a CIF file. Using the builder functionality in AMSinput, randomly insert 51 lithium atoms into the sulfur matrix using the SMILES code [Li] to generate the Li₀.₄S composition [4]. Alternatively, for amorphous structures, use packing tools like PackMol to create an initial amorphous Li₀.₄S structure containing 2048 sulfur atoms and 819 lithium atoms (2048 × 0.4 = 819) [32].

Geometry Optimization and Simulated Annealing

Following structure generation, perform a geometry optimization including lattice relaxation to equilibrate the system. Use the following parameters: Task = Geometry Optimization; Force Field = LiS.ff; Optimize Lattice = Enabled; Force Tolerance = 0.5 eV/Ã…; Maximum Steps = 1000 [4] [32].

To generate amorphous structures via simulated annealing, implement the following temperature profile using molecular dynamics: (1) Equilibrate at 300 K for 5000 steps; (2) Heat from 300 K to 1600 K over 20000 steps; (3) Rapidly cool from 1600 K to 300 K over 5000 steps [4]. Use a Berendsen thermostat with a damping constant of 100 fs throughout this process. Finally, perform another geometry optimization with lattice relaxation to obtain the equilibrated amorphous Liâ‚€.â‚„S structure for production MD simulations.

Workflow Visualization

The following diagram illustrates the complete computational workflow for determining lithium diffusion coefficients in Liâ‚€.â‚„S cathode material:

workflow Start Start Import Import CIF Structure Start->Import End End Build Build Li₀.₄S System (Insert 51 Li atoms) Import->Build Opt1 Geometry Optimization with Lattice Relaxation Build->Opt1 Anneal Simulated Annealing MD (300K→1600K→300K) Opt1->Anneal Opt2 Final Geometry Optimization with Lattice Relaxation Anneal->Opt2 ProdMD Production MD at Target T (110,000 steps, 1600 K) Opt2->ProdMD MSD MSD Analysis ProdMD->MSD VACF VACF Analysis ProdMD->VACF Arrhenius Arrhenius Extrapolation (Multiple Temperatures) MSD->Arrhenius VACF->Arrhenius Arrhenius->End

Diagram 1: Complete workflow for calculating Li diffusion coefficients in Liâ‚€.â‚„S

Production MD Simulation and Diffusion Coefficient Calculation

Production Molecular Dynamics Parameters

For the production MD simulation to compute diffusion coefficients, use the following parameters: Task = Molecular Dynamics; Number of Steps = 110000; Sample Frequency = 5 (writes atomic positions and velocities every 5 steps); Thermostat = Berendsen; Temperature = 1600 K; Damping Constant = 100 fs [4]. The simulation should include 10000 steps for equilibration followed by 100000 production steps. With a typical time step of 0.25 fs, the time between trajectory outputs will be samplefrequency × timestep = 5 × 0.25 fs = 1.25 fs [4].

Diffusion Coefficient Calculation Methods

Mean Squared Displacement (MSD) Method

The diffusion coefficient can be calculated through the slope of the mean squared displacement using the following equations [4]:

[MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle]

[D = \textrm{slope(MSD)}/6]

In AMSmovie, set the following parameters for MSD analysis: Steps = 2000-22001; Atoms = Li; Max MSD Frame = 5000 (corresponding to 5000 × 1.25 fs = 6250 fs) [4]. Generate the MSD plot and ensure the MSD line is straight, indicating sufficient simulation time for adequate statistics. The diffusion coefficient D is obtained from the slope of the MSD curve divided by 6 (or 2 for two-dimensional systems).

Velocity Autocorrelation Function (VACF) Method

Alternatively, the diffusion coefficient can be determined by integrating the velocity autocorrelation function:

[D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t]

In AMSmovie, set these parameters for VACF analysis: Steps = 2000-22001; Property = Diffusion Coefficient (D); Atoms = Li; Max ACF Step = 5000 [4]. The bottom plot shows the integral of the VACF divided by 3, which should converge to a constant value for large enough times, providing the diffusion coefficient.

Analysis Methodology Visualization

The following diagram illustrates the two primary methods for calculating diffusion coefficients from MD trajectories:

analysis MDTrajectory MD Trajectory Data (Positions & Velocities) MSD MSD Analysis MDTrajectory->MSD VACF VACF Analysis MDTrajectory->VACF LinearFit Linear Regression on MSD(t) curve MSD->LinearFit Integration Integrate VACF over time VACF->Integration D_MSD D = slope(MSD)/6 LinearFit->D_MSD D_VACF D = ⅓∫VACF(t)dt Integration->D_VACF Comparison Compare Results (Should be similar) D_MSD->Comparison D_VACF->Comparison

Diagram 2: Two primary methods for calculating diffusion coefficients from MD

Data Analysis and Interpretation

Quantitative Results and Method Comparison

Table 2: Diffusion Coefficient Results for Liâ‚€.â‚„S at 1600 K

Analysis Method Diffusion Coefficient (m²/s) Key Parameters Convergence Criteria
MSD Analysis 3.09 × 10⁻⁸ [4] Max MSD Frame: 5000 (6250 fs) [4] Straight line in MSD plot [4]
VACF Analysis 3.02 × 10⁻⁸ [4] Max ACF Step: 5000 (6250 fs) [4] Horizontal plateau in D(t) plot [4]

Both methods should yield approximately equal values for the diffusion coefficient, as demonstrated in the table above. The MSD method is generally recommended due to its simpler implementation and more straightforward interpretation [4]. If the MSD line is not straight or the D(t) curve does not reach a horizontal plateau, longer simulations are needed to gather better statistics [4].

Extrapolation to Lower Temperatures

Calculating diffusion coefficients directly at room temperature (300 K) would require prohibitively long MD simulations. Instead, perform simulations at multiple elevated temperatures and extrapolate using the Arrhenius equation [4]:

[D(T) = D0 \exp{(-Ea / k_{B}T)}]

[\ln{D(T)} = \ln{D0} - \frac{Ea}{k_{B}}\cdot\frac{1}{T}]

where (D0) is the pre-exponential factor, (Ea) is the activation energy, (k_B) is the Boltzmann constant, and (T) is the temperature [4]. Calculate trajectories for at least four different temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K), then extract the activation energy and pre-exponential factor from an Arrhenius plot of (\ln{(D(T))}) against (1/T) [4]. This approach provides an upper bound for the lithium diffusion coefficient at room temperature.

Critical Considerations for Accurate Results

Several factors must be considered to ensure accurate diffusion coefficient calculations. Finite-size effects significantly influence results, as the diffusion coefficient depends on supercell size unless the cell is very large [4]. Typically, simulations should be performed for progressively larger supercells with extrapolation to the "infinite supercell" limit [4]. Additionally, the ReaxFF force field demonstrates strong sensitivity to the training set, making accurate parametrization crucial for reliable results [8]. Recent enhancements to ReaxFF for lithium-ion systems have shown two-order-of-magnitude improvements in predicting lithium diffusivity at room temperature when properly parameterized [8].

This application note provides a comprehensive protocol for calculating lithium diffusion coefficients in Li₀.₄S cathode materials using ReaxFF molecular dynamics simulations. The methodology encompasses system preparation through simulated annealing, production MD simulations at elevated temperatures, and diffusion coefficient calculation via MSD and VACF analyses. The computed diffusion coefficient of approximately 3.0 × 10⁻⁸ m²/s at 1600 K provides a baseline for evaluating lithium transport in sulfur cathode materials. For accurate room-temperature predictions, researchers should implement the Arrhenius extrapolation method using data from multiple temperatures. This protocol offers battery researchers a robust framework for computationally evaluating transport properties in lithium-sulfur battery cathode materials, contributing to the ongoing development of advanced energy storage systems.

Within the framework of ReaxFF molecular dynamics (MD), calculating the diffusion coefficient (D) of ions, such as lithium in battery materials, is a fundamental analysis for predicting material performance. Two primary methods exist for extracting this coefficient from an MD trajectory: the Mean Squared Displacement (MSD) approach and the Velocity Autocorrelation Function (VACF) method [4]. While setting up and running the simulation is a crucial first step, correctly interpreting the resulting data is paramount for obtaining physically meaningful and reliable values for the diffusion coefficient. This application note provides detailed protocols and analytical guidance for interpreting MSD slopes and assessing VACF convergence, critical steps in ReaxFF-based diffusion studies.

Theoretical Foundation of Diffusion in ReaxFF

The ReaxFF force field enables the simulation of chemical reactivity by using a bond-order-dependent potential function. Unlike simple harmonic force fields, ReaxFF calculates the bond order between atoms based on their interatomic distance at each step, allowing bonds to break and form dynamically [33]. The total energy of the system includes bond, over-coordination, valence angle, torsion, and non-bonded (van der Waals and Coulomb) terms, providing a comprehensive description of the system's reactivity and dynamics [33] [34].

Within this framework, the diffusion of an atom is governed by its interactions with the surrounding chemical environment. The two main methods for calculating the diffusion coefficient from an MD trajectory are:

  • Mean Squared Displacement (MSD): This method is based on the statistical displacement of particles over time. For three-dimensional diffusion, the diffusion coefficient is related to the slope of the MSD versus time plot [4]: ( MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ) ( D = \frac{\textrm{slope(MSD)}}{6} )

  • Velocity Autocorrelation Function (VACF): This method analyzes the correlation of a particle's velocity with its own velocity at a later time. The diffusion coefficient is obtained from the integral of the VACF [4]: ( D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t )

The ReaxFF method provides a powerful means to simulate these processes in complex, reactive systems, such as lithium-ion battery electrodes, where chemical environment significantly influences ion mobility [4] [8].

Analytical Protocol 1: Diffusion Coefficient via MSD Slope

The MSD method is generally recommended for its straightforward interpretation, relying on a linear fit to the MSD curve [4].

Step-by-Step Procedure

  • Production Simulation: Run a sufficiently long ReaxFF MD simulation at a constant target temperature (e.g., 1600 K). Ensure the trajectory is saved at a consistent sampling frequency (e.g., every 5 steps) [4].
  • Trajectory Analysis: Load the resulting trajectory file into an analysis tool like AMSmovie.
  • MSD Calculation:
    • Select the atom type of interest (e.g., Li).
    • Define the time range for analysis, excluding the initial equilibration steps (e.g., from step 2000 to 22001).
    • Set the Max MSD Frame to a value that provides a good statistical average (e.g., 5000 frames). The corresponding physical time is Max MSD Frame * sample_frequency * time_step [4].
  • Generate MSD Plot: The software will generate a plot of the MSD and a corresponding plot for D, which is the slope of the MSD divided by 6, calculated over an increasing time window.

Interpretation and Troubleshooting MSD Data

A successful MSD analysis requires the MSD curve to be a straight line over a significant time range, indicating normal, Fickian diffusion. The derived D curve should ideally be perfectly horizontal, signifying convergence.

Table 1: Troubleshooting MSD Analysis

Observation Potential Cause Solution
MSD curve is not linear Insufficient simulation time; anomalous diffusion. Run a longer MD simulation to improve statistics [4].
Derived D curve is not horizontal, showing a positive or negative drift. Statistics are insufficient, or the "Start Time Slope" is set too early, including non-diffusive regime data. Increase simulation length. Ensure the linear fit starts at a time (Start Time Slope) where ballistic motion has ceased and diffusive behavior dominates [4].
MSD values are too small or do not grow. The ion mobility is very low, or the system size is too small leading to finite-size effects. For low temperatures, calculate D at higher temperatures and extrapolate using the Arrhenius equation. Use a larger supercell and extrapolate to the infinite-cell limit [4].

Analytical Protocol 2: Diffusion Coefficient via VACF Convergence

The VACF method offers an alternative approach, which can be more sensitive to the local chemical environment and vibrational properties of the diffusing species.

Step-by-Step Procedure

  • Simulation Setup: The MD simulation setup is identical to the MSD approach, with a critical requirement to save atomic velocities to the trajectory by setting an appropriate Sample frequency [4].
  • VACF Calculation:
    • In the analysis software (e.g., AMSmovie), select the "Autocorrelation function" property.
    • Set the analysis steps, again excluding equilibration.
    • Select Property → Diffusion Coefficient (D) and set the Atoms to the relevant type (e.g., Li).
    • Define the Max ACF Step (e.g., 5000) [4].
  • Generate Plots: The analysis will typically generate three plots: the VACF itself, its Fourier transform (power spectrum), and the key result—the integral of the VACF divided by 3, which is the diffusion coefficient D as a function of the integration time上限 (t~max~).

Assessing VACF Convergence

The central challenge of the VACF method is to determine when the integral has converged. A perfectly converged D vs. t~max~ plot will become perfectly horizontal for large t~max~ [4].

Table 2: Troubleshooting VACF Convergence

Observation Interpretation Action
The D curve plateaus to a constant value. Successful Convergence. The value at the plateau is the computed diffusion coefficient. Record the value from the flat region of the curve.
The D curve continues to increase or decrease without forming a clear plateau. Lack of Convergence. The simulation time may be too short for the VACF to fully decay and for its integral to converge. The simulation trajectory must be extended to capture the full decay and integration of the VACF.
The D curve is noisy. Poor statistics. Increase the length of the production simulation to improve averaging.

Comparative Analysis and Data Presentation

For robust results, it is good practice to compute the diffusion coefficient using both MSD and VACF methods. The values obtained should be approximately equal, providing a cross-validation of the analysis [4]. For instance, in a tutorial for Li~0.4~S, the MSD method yielded D = 3.09 × 10⁻⁸ m² s⁻¹, while the VACF method gave D = 3.02 × 10⁻⁸ m² s⁻¹, demonstrating excellent agreement [4].

Table 3: Comparison of MSD and VACF Methods for Diffusion Coefficient Calculation

Feature MSD Method VACF Method
Fundamental Formula ( D = \frac{\textrm{slope(MSD)}}{6} ) ( D = \frac{1}{3} \int{0}^{t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t )
Key Diagnostic Linearity of the MSD plot. Plateau in the integrated VACF plot.
Computational Note Can use a lower sampling frequency (larger Sample frequency), resulting in smaller trajectory files [4]. Requires saving velocities at a high frequency (smaller Sample frequency), leading to larger files [4].
Primary Advantage Intuitive and straightforward to interpret. Provides insight into local dynamics and vibrational modes via the power spectrum.
Common Challenge Ensuring a linear regime is reached. Ensuring the integral converges within the simulation time.

The following workflow diagram summarizes the logical relationship between the simulation and the two analysis pathways:

Start ReaxFF MD Production Run Trajectory Trajectory Data (Positions & Velocities) Start->Trajectory MSD MSD Analysis Trajectory->MSD VACF VACF Analysis Trajectory->VACF CheckMSD Is MSD linear? MSD->CheckMSD CheckVACF Does D(t) plateau? VACF->CheckVACF CheckMSD->Start No Run longer simulation ResultMSD D = slope(MSD)/6 CheckMSD->ResultMSD Yes CheckVACF->Start No Run longer simulation ResultVACF D = ⅓ ∫ VACF dt CheckVACF->ResultVACF Yes Compare Compare D from both methods ResultMSD->Compare ResultVACF->Compare End Report Diffusion Coefficient D Compare->End

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 4: Key Computational "Reagents" for ReaxFF Diffusion Studies

Item Function / Description Example / Note
ReaxFF Force Field A parameter set defining reactive interactions between atoms. Must be tailored to the chemical system. e.g., LiS.ff for lithium-sulfur systems [4]. Multiple "branches" exist for different chemistries (e.g., aqueous, combustion) [34].
Initial Structure File The atomic-level starting configuration of the system. Can be imported from a Crystallographic Information File (.cif) or built manually [4].
MD Engine with ReaxFF Software that performs the numerical integration of the equations of motion using the ReaxFF potential. e.g., The AMS software package with the ReaxFF engine [4].
Thermostat Algorithm to control temperature during MD simulations. e.g., Berendsen thermostat used for simulated annealing and production runs [4].
Trajectory Analysis Tool Software for post-processing MD trajectories to compute properties like MSD and VACF. e.g., AMSmovie, which can generate MSD and VACF plots directly [4]. Other common tools include VMD with plugins, and MDAnalysis.
Methyl sorbateMethyl sorbate, CAS:689-89-4, MF:C7H10O2, MW:126.15 g/molChemical Reagent
Ethyl HeptanoateEthyl Heptanoate, CAS:106-30-9, MF:C9H18O2, MW:158.24 g/molChemical Reagent

Advanced Application: Extrapolation to Lower Temperatures

Directly calculating diffusion coefficients at low temperatures (e.g., 300 K) can be computationally prohibitive due to slow ion dynamics. A practical solution is to use the Arrhenius relationship to extrapolate from higher temperatures [4].

Protocol:

  • Calculate the diffusion coefficient D(T) at a minimum of four different elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) [4].
  • Plot the natural logarithm of D (ln D) against the inverse temperature (1/T).
  • Perform a linear fit. The slope of the line is -E~a~/k~B~, from which the activation energy E~a~ can be derived, and the intercept is ln D~0~, the pre-exponential factor [4]: ( \ln{D(T)} = \ln{D0} - \frac{Ea}{k_{B}}\cdot\frac{1}{T} )
  • Use the fitted parameters to calculate D(T) at the desired lower temperature.

This approach provides an efficient upper-bound estimate for low-temperature diffusion, making it invaluable for screening materials.

Overcoming Computational Challenges: Finite-Size Effects and Parameterization

In molecular dynamics (MD) simulations, the computed values of diffusion coefficients are strongly influenced by the size of the simulation box, a phenomenon known as the finite-size effect. For reactive force field (ReaxFF) MD simulations, which are computationally intensive, using small systems is often necessary, making it crucial to understand and correct for these artifacts. This application note provides a detailed protocol for addressing finite-size effects in ReaxFF MD simulations of diffusion coefficients, enabling researchers to obtain results representative of the thermodynamic limit.

Theoretical Foundation of Finite-Size Effects

Molecular dynamics simulations model a finite number of particles (N) in a periodic simulation box. A key finding from hydrodynamic theory is that the self-diffusion coefficient (D_self) computed from such simulations exhibits a systematic dependence on the system size, scaling linearly with the inverse of the box length (L) [35].

The primary origin of this finite-size effect lies in the hydrodynamic self-interactions of a particle in a periodic system. The Yeh and Hummer (YH) correction provides an analytical framework to compensate for this artifact, enabling the estimation of the diffusion coefficient at the thermodynamic limit (D_∞) from finite-size MD results [35]. For self-diffusion, the correction is:

Dself^∞ = Dself + (k_B T ξ)/(6 π η L)

where:

  • D_self is the finite-size self-diffusion coefficient obtained from MD
  • k_B is the Boltzmann constant
  • T is the temperature
  • η is the shear viscosity of the system
  • L is the side length of the (cubic) simulation box
  • ξ is a dimensionless constant (2.837297 for cubic boxes with periodic boundary conditions) [35]

For Maxwell-Stefan (MS) diffusion coefficients, which describe collective mass transport, the finite-size dependency is more complex and also involves the thermodynamic factor (Γ), a measure of the mixture's non-ideality. A correction term analogous to the YH correction has been proposed for MS diffusivities [35].

Table 1: Key Quantities in Finite-Size Correction for Diffusion Coefficients

Quantity Description Method of Calculation
D_self Self-diffusion coefficient from finite MD simulation Mean-squared displacement (MSD) analysis
D_MS Maxwell-Stefan diffusion coefficient from finite MD simulation Mean-squared displacement (MSD) analysis of collective motion
η Shear viscosity Green-Kubo relation (autocorrelation of stress tensor)
Γ Thermodynamic Factor Measures non-ideality from equation of state
L Simulation box length Directly from simulation box dimensions

Quantitative Finite-Size Effects Data

The magnitude of finite-size corrections can be significant. Studies on binary Lennard-Jones systems and various molecular mixtures have demonstrated that the discrepancy between finite-size and thermodynamic-limit diffusivities increases with system non-ideality [35].

Table 2: Magnitude of Finite-Size Effects in Different Scenarios

System Type Observed Finite-Size Effect Required Correction
Lennard-Jones Mixtures Strong dependency of MS diffusivities on number of molecules (N); values increase with N [35] Significant, especially near demixing
Mixtures close to demixing Finite-size correction can be larger than the simulated (finite-size) MS diffusivity [35] Essential for meaningful results
Systems with strong electrostatic interactions YH correction may require rescaling due to strong electrostatic interactions [35] Apply with caution; may need modification

Protocols for Addressing Finite-Size Effects

Protocol 1: System Size Extrapolation

This protocol involves running simulations at multiple system sizes and extrapolating to the thermodynamic limit.

  • System Preparation: Create multiple simulation cells of the same composition but different sizes (e.g., 2x2x2, 3x3x3, 4x4x4 supercell expansions). Ensure the smallest system is large enough to avoid other spurious finite-size effects related to the interaction cutoff.
  • Equilibration: For each system size, perform a full ReaxFF MD equilibration protocol (e.g., NPT ensemble) to relax the density at the target temperature and pressure.
  • Production MD: Run a well-equilibrated NVT simulation for each system size, saving the trajectory with sufficient frequency (e.g., every 1-5 steps for ReaxFF). The total simulation time must be long enough for reliable diffusivity calculation.
  • Diffusivity Calculation: For each system size (L), calculate the self-diffusion coefficient (Dself) from the slope of the mean-squared displacement (MSD) using the Einstein relation:
    • MSD(t) = ⟨[r(0) - r(t)]²⟩
    • Dself = slope(MSD) / (6 * d), where d=3 for 3D systems [4].
  • Extrapolation: Plot the calculated Dself values against 1/L. Perform a linear fit. The y-intercept (at 1/L = 0) corresponds to the diffusion coefficient at the thermodynamic limit, Dself^∞.

Protocol 2: Applying the Analytical Yeh-Hummer Correction

This protocol is more computationally efficient as it requires only a single system size, but relies on an accurate viscosity calculation.

  • Single System Simulation: Perform a production NVT ReaxFF MD simulation for a single, sufficiently large system.
  • Diffusivity Calculation: Calculate the finite-size self-diffusion coefficient (D_self) from the MSD as in Protocol 1, Step 4.
  • Viscosity Calculation: Compute the shear viscosity (η) from the same trajectory using the Green-Kubo formula, which integrates the autocorrelation function of the off-diagonal elements of the stress tensor (Pαβ) [35]:
    • η = (V / kB T) ∫₀^∞ ⟨Pαβ(0) Pαβ(t)⟩ dt
    • where V is the volume of the system. Averaging over the three independent off-diagonal components (xy, xz, yz) improves statistics.
  • Application of Correction: Apply the YH correction using the box length (L) and calculated viscosity (η) to obtain the corrected diffusivity: Dself^∞ = Dself + (k_B T ξ)/(6 Ï€ η L).

Protocol for Maxwell-Stefan Diffusivities

For mutual diffusion, follow a similar approach to Protocol 2, but use the appropriate correction for Maxwell-Stefan diffusivities, which incorporates the thermodynamic factor [35]. The thermodynamic factor must be determined from separate simulations or equations of state.

finite_size_workflow start Start: Define System strategy_choice Choose Protocol start->strategy_choice p1 Protocol 1: Multi-Size Extrapolation strategy_choice->p1  For MS diffusivities or high precision p2 Protocol 2: Analytical YH Correction strategy_choice->p2  For self-diffusion  More efficient sim_p1 Run MD at multiple system sizes (L1, L2, ...) p1->sim_p1 sim_p2 Run MD at a single system size (L) p2->sim_p2 calc_d_p1 Calculate D_self(L) for each size sim_p1->calc_d_p1 calc_d_p2 Calculate finite-size D_self from MSD sim_p2->calc_d_p2 extrapolate Plot D_self vs 1/L Extrapolate to 1/L -> 0 calc_d_p1->extrapolate calc_eta Calculate shear viscosity (η) calc_d_p2->calc_eta apply_corr Apply formula: D_∞ = D_self + kBTξ / 6πηL calc_eta->apply_corr result Result: D_self at Thermodynamic Limit extrapolate->result apply_corr->result

Workflow for Addressing Finite-Size Effects

The Scientist's Toolkit

Table 3: Essential Research Reagent Solutions for ReaxFF Diffusion Studies

Tool / Material Function / Description Application Notes
ReaxFF Force Field A reactive force field describing bond formation/breaking. Parameterized for specific elements (e.g., C-H-O-Li-F) [8]. Must be carefully selected and validated for the chemical system under study.
ReaxFF MD Software Software capable of performing ReaxFF MD simulations (e.g., AMS, LAMMPS). Should support calculation of MSD and stress tensor for viscosity.
Visualization & Analysis Suite Software for trajectory analysis (e.g., AMSmovie [4], VARMD [36], custom scripts). Critical for calculating MSD, VACF, and other properties from MD trajectories.
System Builder Tools Tools for creating initial structures (e.g., AMSinput builder [4], grand canonical Monte Carlo for insertion [4]). Used to generate supercells of varying sizes with correct composition.
Yeh-Hummer Correction Script Custom or published code for implementing the finite-size analytical correction. Automates the application of the correction formula using simulated L, T, η, and D.
Ethyl tridecanoateEthyl tridecanoate, CAS:28267-29-0, MF:C15H30O2, MW:242.40 g/molChemical Reagent
2-Thiophenemethanol2-Thiophenemethanol, CAS:636-72-6, MF:C5H6OS, MW:114.17 g/molChemical Reagent

In molecular dynamics (MD) simulations, statistical accuracy is paramount for deriving meaningful physical properties, such as diffusion coefficients, from generated trajectories. The reliability of these results is not a given; it is contingent upon simulation length, appropriate sampling, and the application of robust convergence criteria. Within the context of ReaxFF reactive force-field simulations, where computational cost is a significant consideration, strategically planning the simulation protocol to ensure results are both statistically sound and computationally feasible is a critical concern for researchers. This document provides detailed application notes and protocols for ensuring the statistical accuracy of diffusion coefficient calculations within ReaxFF MD simulations, framed specifically for a thesis on this topic.

Theoretical Foundation of Diffusion in ReaxFF MD

The ReaxFF reactive force-field provides a powerful platform for simulating reactive chemistry in complex materials, such as those in lithium-ion batteries. By employing a bond-order formalism, ReaxFF allows for dynamic bond formation and breaking during simulations, which is essential for studying evolving systems [2]. The force field calculates system energy as a sum of various contributions, including bond energy, angle strain, torsional energy, and non-bonded Coulomb and van der Waals interactions [2].

Within this framework, the self-diffusion coefficient (D) is a key dynamic property that quantifies the mean drift velocity of particles under a concentration gradient. In MD simulations, it is typically calculated through one of two primary methods:

  • Via the Mean Squared Displacement (MSD): This is the most common and recommended approach. The diffusion coefficient is derived from the slope of the MSD over time, as described by the Einstein relation [4]: ( MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ) ( D = \frac{\textrm{slope(MSD)}}{6} ) (for 3-dimensional diffusion)

  • Via the Velocity Autocorrelation Function (VACF): This method involves integrating the VACF over time [4]: ( D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t )

The MSD method is generally preferred for its straightforward implementation and interpretation [4].

Quantitative Parameters for Simulation Length and Analysis

Determining the appropriate simulation length and analysis parameters is crucial for statistical accuracy. The table below summarizes key quantitative parameters derived from a ReaxFF tutorial on calculating diffusion coefficients for Lithium ions in a Li~0.4~S cathode [4].

Table 1: Key Simulation Parameters for Diffusion Coefficient Calculation

Parameter Value / Range Purpose and Rationale
Total Production MD Steps 100,000 Provides sufficient trajectory data for analysis after equilibration.
Equilibration Steps 10,000 Allows the system to reach a steady state at the target temperature before production run.
Integration Time Step 0.25 fs Ensures numerical stability for the ReaxFF potential [4].
Sampling Frequency 5 steps Writes atomic positions/velocities every 1.25 fs (5 * 0.25 fs). A higher frequency can be used for MSD to reduce file size [4].
Temperature 1600 K Elevated temperature enhances ion mobility, making diffusion observable on shorter timescales [4].
MSD Slope Calculation Start Time 2000 steps Avoids the initial ballistic regime of particle motion where MSD is quadratic in time [4].
Max MSD/ACF Frame 5000 frames Corresponds to a maximum time of 6250 fs for the diffusion analysis [4].

Protocols for Calculating and Validating Diffusion Coefficients

Mean Squared Displacement (MSD) Protocol

This protocol outlines the steps for calculating the diffusion coefficient using the recommended MSD method within the AMS software environment [4].

Procedure:

  • Run Production MD: Execute a ReaxFF MD simulation following the parameters in Table 1, ensuring the trajectory (positions and velocities) is saved at the specified sampling frequency.
  • Open Trajectory in AMSmovie: Load the resulting trajectory file (.rkf) in the AMSmovie analysis tool.
  • Generate MSD Plot:
    • Navigate to MD Properties → MSD.
    • Set the Steps range for analysis (e.g., 2000 - 22001) to exclude the equilibration period.
    • Set the Atoms selector to the diffusing species of interest (e.g., Li).
    • Set the Max MSD Frame to 5000 (or a value corresponding to a time where the MSD remains linear).
    • Click Generate MSD.
  • Analyze Results and Extract D:
    • The software will generate an MSD vs. time plot and a second curve showing the instantaneous diffusion coefficient (slope/6).
    • A statistically accurate result is indicated by a straight, linear MSD plot. The diffusion coefficient D is the converged value of the instantaneous D curve. For example, a value converging to ~3.09 × 10⁻⁸ m² s⁻¹ is reported [4].
    • Convergence Criterion: If the MSD plot is not straight or the instantaneous D curve has not plateaued, the simulation must be extended to gather more statistics [4].

Velocity Autocorrelation Function (VACF) Protocol

This protocol provides an alternative method for calculating the diffusion coefficient, which requires a higher sampling frequency (smaller Sample frequency value) [4].

Procedure:

  • Run Production MD with High Sampling: Ensure the MD simulation was run with a sufficiently high sampling frequency to capture velocity correlations.
  • Open Trajectory in AMSmovie: Load the trajectory in AMSmovie.
  • Generate Autocorrelation Function:
    • Navigate to MD Properties → Autocorrelation function.
    • Set the Steps range (e.g., 2000 - 22001).
    • Select Property → Diffusion Coefficient (D).
    • Set the Atoms to the diffusing species (e.g., Li).
    • Set the Max ACF Step to 5000.
    • Click Generate ACF.
  • Analyze Results and Extract D:
    • The tool will generate three plots. The bottom plot shows the integral of the VACF divided by 3, which is the diffusion coefficient D.
    • Convergence Criterion: The D curve must become perfectly horizontal (converge) for large enough times. The reported value (e.g., 3.02 × 10⁻⁸ m² s⁻¹) should be approximately equal to the MSD-derived value [4].

Workflow for Statistical Accuracy

The following diagram illustrates the integrated workflow for running a simulation and applying both analysis protocols to ensure a statistically robust result.

G Start Start: Define System and Objectives MD_Setup MD Simulation Setup (Task: Molecular Dynamics) Start->MD_Setup Param_Table Apply Parameters from Table 1 MD_Setup->Param_Table Run_Sim Run Production MD Simulation Param_Table->Run_Sim Analyze_MSD Analyze via MSD Protocol Run_Sim->Analyze_MSD Analyze_VACF Analyze via VACF Protocol Run_Sim->Analyze_VACF Check_Conv_MSD MSD linear and D curve flat? Analyze_MSD->Check_Conv_MSD Check_Conv_VACF D curve converged? Analyze_VACF->Check_Conv_VACF Result Report Diffusion Coefficient D Check_Conv_MSD->Result Yes Extend_Sim Extend Simulation Length Check_Conv_MSD->Extend_Sim No Check_Conv_VACF->Result Yes Check_Conv_VACF->Extend_Sim No Extend_Sim->Analyze_MSD Extend_Sim->Analyze_VACF

Diagram 1: Workflow for MD Simulation and Convergence Analysis

Advanced Considerations and Extrapolation

Addressing Finite-Size Effects

A critical consideration for statistical accuracy is the system size. A simulation's diffusion coefficient can be influenced by the finite size of the simulation box, an effect known as finite-size effects. The ReaxFF tutorial highlights that "because of finite-size effects, the diffusion coefficient depends on the size of the supercell (unless the supercell is very large)." [4]. The recommended practice to mitigate this is to perform simulations for progressively larger supercells and extrapolate the calculated diffusion coefficients to the "infinite supercell" limit [4].

Extrapolation to Lower Temperatures

Calculating diffusion coefficients at experimentally relevant temperatures (e.g., 300 K) can be prohibitively expensive due to the long simulation times required to observe sufficient diffusion events. A practical solution is to use an Arrhenius extrapolation from higher temperatures [4].

Protocol for Arrhenius Extrapolation:

  • Calculate D at Multiple Temperatures: Perform MD simulations and calculate the diffusion coefficient D for at least four different elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) [4].
  • Create an Arrhenius Plot: Plot the natural logarithm of D against the inverse temperature, 1/T.
  • Perform Linear Fit: Fit the data points to the Arrhenius equation: ( \ln{D(T)} = \ln{D0} - \frac{Ea}{k_{B}}\cdot\frac{1}{T} ) where D~0~ is the pre-exponential factor and E~a~ is the activation energy.
  • Extrapolate: Use the linear fit to extrapolate the value of D to the lower temperature of interest.

Parameterization and Limitations

The accuracy of any ReaxFF simulation is fundamentally tied to the quality of its parameter set. Force fields are parameterized against training data from quantum mechanical (QM) calculations and experiments [37]. Recent studies emphasize that ReaxFF can be highly sensitive to its training set, making its ability to interpolate the potential energy surface challenging [8]. Therefore, it is crucial to use a parameter set that has been validated for the specific chemical system under investigation. Interactive reparameterization protocols, which focus on matching key properties like crystal structure and mass transport, are emerging to enhance accuracy for specific applications like lithium-ion battery components [8].

The Scientist's Toolkit: Research Reagent Solutions

Table 2: Essential Computational Tools for ReaxFF Diffusion Studies

Tool / Resource Function / Purpose
AMS Software Suite An integrated platform containing the engine for running ReaxFF MD simulations and the AMSmovie tool for trajectory analysis [4].
ReaxFF Force Field File (.ff) A parameter file defining the interatomic potential for the specific set of elements in the system (e.g., LiS.ff, CHONSMgPNaFBLi-e.ff) [4] [38].
Initial Structure File The atomic coordinates of the system to be simulated, typically in .xyz or .cif format [4].
Python & PLAMS Library Scripting environment for automating simulation setup, analysis, and post-processing, including calculating time-averaged properties [4] [8].
Validation Dataset (QM/Experimental) Reference data (e.g., from DFT, CCSD(T), or experiments) used to validate the force field's predictions and for Arrhenius plot anchoring [4] [37] [8].

Optimizing Sampling Frequency for MSD vs. VACF Calculations

In molecular dynamics (MD) simulations, accurately calculating transport properties like the diffusion coefficient (D) is fundamental to understanding material behavior. The Mean Squared Displacement (MSD) and Velocity Autocorrelation Function (VACF) are two primary methods for this calculation [4]. However, these methods have divergent requirements for sampling frequency—the rate at which atomic coordinates and velocities are recorded from the simulation trajectory. Optimizing this frequency is critical to balancing computational resources, disk space, and statistical accuracy. This application note, framed within ReaxFF MD tutorial research, provides a detailed protocol for selecting the appropriate sampling strategy for MSD and VACF analyses, complete with quantitative guidelines and step-by-step methodologies [4].

Theoretical Background: MSD and VACF

The diffusion coefficient describes the rate at which particles diffuse through a material. In MD simulations, it can be derived from particle trajectories using two core approaches:

  • The Mean Squared Displacement (MSD) is defined as ( MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ), where (\textbf{r}(0)) and (\textbf{r}(t)) are the particle's position at time zero and time (t), respectively. The diffusion coefficient is obtained from the slope of the MSD versus time plot: ( D = \frac{\textrm{slope(MSD)}}{6} ) for 3-dimensional diffusion [4]. The MSD is a spatial method that tracks the net displacement of particles over time.

  • The Velocity Autocorrelation Function (VACF) is defined as ( \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle ), the dot product of a particle's velocity vector at time zero and time (t), averaged over all particles in the ensemble [39]. The diffusion coefficient is calculated by integrating the VACF over time: ( D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t ) [4]. In contrast to MSD, the VACF is a dynamic method that probes the nature of atomic motions and memory effects in the system.

The fundamental difference in what these functions measure—cumulative displacement versus the correlation of instantaneous velocities—directly informs their differing sensitivities to sampling frequency.

Sampling Frequency: A Comparative Analysis

Table 1: Key Differences in Sampling Frequency Requirements for MSD and VACF

Feature Mean Squared Displacement (MSD) Velocity Autocorrelation Function (VACF)
Core Requirement Sufficient points to accurately define the linear slope over time. High-frequency data to capture rapid velocity decorrelation.
Recommended Sampling Lower frequency is acceptable (e.g., every 10-50 steps) [4]. Higher frequency is required (e.g., every 1-5 steps) [4].
Trajectory File Size Smaller files due to less frequent coordinate writing. Larger files due to more frequent velocity writing.
Key Consideration The time between saved frames must be short enough to prevent aliasing and to establish a reliable linear fit, but can be relatively coarse. The time interval must be shorter than the fastest physical process causing velocity decorrelation (e.g., bond vibrations) to avoid signal aliasing [40].
Computational Tip "If you use the MSD to calculate the diffusion coefficient, you can set Sample frequency to a higher number (giving a smaller trajectory file)." [4] "This requires setting sampling frequency to a small number" to capture the high-frequency components of the motion [4].

Practical Considerations and Protocols

Workflow for Diffusion Coefficient Calculation

The following diagram illustrates the general workflow for calculating diffusion coefficients, highlighting the decision point between MSD and VACF analysis and their respective sampling needs.

G Start Start: ReaxFF MD Simulation Setup Define Sampling Frequency Start->Setup Decision Primary Analysis Method? Setup->Decision MSDpath MSD Analysis Path Decision->MSDpath  MSD VACFpath VACF Analysis Path Decision->VACFpath  VACF LowFreq Set Lower Sampling Frequency MSDpath->LowFreq HighFreq Set Higher Sampling Frequency VACFpath->HighFreq Run Run Production MD LowFreq->Run HighFreq->Run AnalyzeMSD Calculate MSD and Linear Fit for D Run->AnalyzeMSD AnalyzeVACF Calculate VACF and Integrate for D Run->AnalyzeVACF Compare Compare D Values AnalyzeMSD->Compare AnalyzeVACF->Compare End Report Diffusion Coefficient Compare->End

Step-by-Step Protocol for a ReaxFF MD Simulation

This protocol is adapted from a tutorial on computing Li-ion diffusion coefficients in a Li(_{0.4})S cathode system using ReaxFF [4].

Part A: System Setup and Equilibration
  • Import and Build System: Import the crystal structure (e.g., from a CIF file). Use the builder tool or Grand Canonical Monte Carlo (GCMC) to insert diffusing species (e.g., Li atoms) [4].
  • Geometry Optimization: Perform a full geometry optimization, including lattice parameters, to relax the system. Use the Optimize lattice checkbox in the AMS software [4].
  • Equilibration MD: Run an NVT or NPT MD simulation to equilibrate the system density and energy at the target temperature. A Berendsen thermostat is often suitable for this step [4].
Part B: Production MD for Diffusion Analysis
  • Set MD Parameters:
    • Task: Molecular Dynamics.
    • Number of Steps: Typically 100,000+ steps for adequate statistics.
    • Time Step: 0.25 fs (for ReaxFF with light atoms like Li) [4].
    • Thermostat: Berendsen or Nose-Hoover, set to the target temperature (e.g., 1600 K for high-temperature estimation) [4].
  • Configure Sampling Frequency (Sample frequency):
    • For MSD-focused analysis: Set to a higher value (e.g., 10-50 steps). This means writing data every 2.5-12.5 fs, resulting in smaller trajectory files [4].
    • For VACF-focused analysis: Set to a lower value (e.g., 1-5 steps). This means writing data every 0.25-1.25 fs, which is critical to capture the fast velocity decorrelation [4].
    • For combined analysis: Favor the VACF requirement. Set Sample frequency to a low value (e.g., 5) to ensure both analyses are viable, accepting the larger file size [4].
  • Run the Simulation.
Part C: Post-Processing and Analysis
  • MSD Analysis:
    • In a tool like AMSmovie, select the diffusing species (e.g., Li).
    • Generate the MSD plot. Set a Max MSD Frame to ensure analysis is done in the linear diffusion regime.
    • The software will perform a linear fit. The diffusion coefficient is ( D = \textrm{slope(MSD)}/6 ) [4].
    • Visually inspect the MSD curve; a straight line indicates normal diffusion and sufficient sampling.
  • VACF Analysis:
    • In AMSmovie, select the 'Autocorrelation function' and set Property to 'Diffusion Coefficient (D)'.
    • Set Atoms to the diffusing species.
    • The tool will compute the VACF, its power spectrum, and the integral. The plateau of the integral divided by 3 gives the diffusion coefficient D [4].
    • The VACF curve should decay smoothly, and its integral should converge to a stable value at long times.

The Scientist's Toolkit: Essential Research Reagents and Computational Tools

Table 2: Key Software and Analysis Tools for Diffusion Coefficient Calculations

Tool / Reagent Function / Purpose Example Use Case
ReaxFF Force Field A reactive force field for atomistic-scale simulations of chemical reactions, capable of modeling bond formation and breaking [41]. Describing interatomic interactions in complex materials like lithiated sulfur cathodes [4].
MD Engine (AMS/LAMMPS) The core software that performs the numerical integration of the equations of motion for the MD simulation. Running the production MD trajectory with specific thermostats and sampling frequencies [4].
Trajectory Analysis Tool (AMSmovie) A specialized tool for post-processing MD trajectories to compute properties like MSD and VACF. Generating MSD plots and performing linear fits to extract the diffusion coefficient slope [4].
Berendsen Thermostat An algorithm to control the simulation temperature by weakly coupling the system to a heat bath. Maintaining the system at a target temperature (e.g., 1600 K) during the production MD run [4].

Selecting an optimal sampling frequency in MD simulations is not a one-size-fits-all parameter but a deliberate choice based on the intended analysis method. For MSD, a lower sampling frequency is sufficient and saves storage, while for VACF, a high sampling frequency is non-negotiable to accurately capture the fast dynamics of velocity decorrelation. By following the detailed protocols and guidelines presented here, researchers can reliably compute diffusion coefficients using the ReaxFF framework, ensuring their conclusions are built upon a solid computational foundation.

Within the framework of ReaxFF molecular dynamics (MD) simulations, precise temperature control is not merely a technical detail but a foundational aspect for obtaining physically meaningful results, particularly in the calculation of material properties such as diffusion coefficients. The thermostat, an algorithmic mechanism applied to regulate the kinetic energy of the system, and its associated damping parameter, which determines the strength of this coupling, are critical choices that can significantly influence the outcome of a simulation. An inappropriate selection can lead to unrealistic dynamics, artificially accelerated or suppressed reaction rates, and ultimately, inaccurate data. This application note, contextualized within a broader thesis on ReaxFF MD tutorials for diffusion coefficient research, provides a detailed protocol for the selection and application of thermostats, with a specific focus on studies investigating lithium-ion transport in battery materials [4] [8]. We will summarize the available methods, provide step-by-step application protocols, and visualize the decision-making workflow to empower researchers in making informed choices.

Thermostat Theory and Available Methods in ReaxFF

In molecular dynamics, thermostats maintain the average temperature of a system by adjusting atom velocities. The damping parameter (Ï„), typically expressed in units of time (e.g., femtoseconds), dictates the relaxation time of the thermostat. A small Ï„ value indicates strong coupling and rapid temperature correction, while a large Ï„ value indicates weak coupling and a more gradual adjustment, approximating the NVE (microcanonical) ensemble more closely. The choice of damping parameter is a balance between the need for effective temperature control and the desire to minimize perturbation of the natural dynamics of the system.

ReaxFF provides several thermostatting algorithms, suitable for different simulation goals. The following table summarizes the key thermostats and their typical applications based on the surveyed documentation and literature.

Table 1: Thermostat Methods in ReaxFF for MD Simulations

Thermostat Method Control Parameter (imdmet) Key Characteristics Primary Application Context
Berendsen [4] 1 Weak coupling; exponentially scales velocities to drive system towards target T. Efficient but does not generate a true canonical ensemble. General purpose equilibration and production runs; commonly used in diffusion studies [4].
Nose-Hoover Chain (NHC) 2 Uses extended Lagrangian to generate a correct canonical (NVT) ensemble. More rigorous but computationally slightly more expensive. Production runs where strict adherence to the canonical ensemble is required.
NVE Ensemble 3 No thermostat; total energy is conserved. Baseline simulations or as the conduction zone in Non-Equilibrium MD (NEMD) for thermal conductivity [42].
Simple Heat Pump 8 Adds/subtracts a fixed amount of kinetic energy to/from predefined zones; used for NEMD. Non-equilibrium methods for calculating thermal conductivity [42].
HEX (Ikeshoji & Hafskjold) 9 A variant of the heat pump that conserves the center-of-mass velocity of the zone. NEMD for thermal conductivity with reduced artifacts [42].

Application Protocols for Diffusion Coefficient Studies

The following protocols outline the specific procedures for applying temperature control in simulations aimed at calculating diffusion coefficients, as demonstrated in studies of lithiated sulfur cathodes [4].

Protocol: Simulated Annealing for Amorphous System Generation

Objective: To generate an amorphous structure of a material (e.g., Li~0.4~S) from a crystalline starting point through a controlled heating and cooling cycle [4].

  • Initialization: In the AMSinput panel, set the Task to Molecular Dynamics.
  • Simulation Length: In the MD details, set the total number of steps to, for example, 30000 with a time step of 0.25 fs.
  • Thermostat Configuration:
    • Navigate to the Thermostat details.
    • Add a new Berendsen thermostat (imdmet=1).
    • In the Temperature(s) field, define the profile: 300 300 1600 300 (in Kelvin). This corresponds to initial constant temperature, heating, and cooling phases.
    • In the Duration(s) field, define the number of MD steps for each segment: 5000 20000 5000.
    • Set the damping constant to 100 fs. This value is large enough to avoid overly aggressive temperature control during the phase transitions.
  • Execution: Run the calculation and monitor the temperature profile in AMSmovie to confirm the system follows the defined regime.

Protocol: Production MD for Mean Squared Displacement (MSD) Analysis

Objective: To run a production MD simulation at a constant, elevated temperature to collect trajectory data for calculating the diffusion coefficient via MSD [4].

  • Initialization: Set the Task to Molecular Dynamics.
  • Simulation Length: Set the number of steps to, for example, 110000, comprising an initial equilibration phase (e.g., 10000 steps) and a production phase (e.g., 100000 steps).
  • Trajectory Sampling: Set the Sample frequency to 5 (or higher). This ensures atomic positions are recorded frequently enough for accurate MSD calculation.
  • Thermostat Configuration:
    • Set the thermostat type to Berendsen (imdmet=1).
    • Set the Temperature to the target production temperature (e.g., 1600 K).
    • Ensure the Duration field is empty for a single, constant-temperature regime.
    • Set the damping constant to 100 fs [4]. This is a commonly used value that provides stable temperature control without severely disrupting ionic diffusion.
  • Execution: Run the calculation. After completion, the trajectory can be analyzed in AMSmovie to compute the MSD and extract the diffusion coefficient using the relation D = slope(MSD)/6.

Protocol: Non-Equilibrium MD for Thermal Conductivity

Objective: To calculate the thermal conductivity of a material by establishing a heat flux and measuring the resulting temperature gradient [42].

  • System Preparation: The simulation cell must be divided into at least three zones: a heat source, a heat sink, and a central conduction zone.
  • Ensemble Selection: Set the imdmet parameter to 3 (NVE ensemble) for the entire system.
  • Method Selection: Choose the NEMD method by setting the itdmet parameter to 2 (default), 8, or 9.
  • Zone Definition via File: Create a tregime.in file to define the zones and their properties. For the itdmet=8/9 "heat pump" methods, the file specifies the amount of kinetic energy (dQ) added/removed per step [42].

  • Analysis: After the simulation reaches a steady state, the temperature gradient is obtained from the tprofile.out file or the KF result file. The heat flow rate is calculated from the fort.75 file (itdmet=2) or from the dQ value and time step (itdmet=8/9). Thermal conductivity is then computed as k = W / (S â‹… grad(T)).

Thermostat Selection Workflow

The following diagram illustrates the decision-making process for selecting and configuring a thermostat in a ReaxFF MD simulation, guiding the researcher through the key questions and resulting protocols.

Start Start: Define Simulation Objective Q1 Is the goal to measure thermal conductivity? Start->Q1 Q2 Is the simulation for system equilibration or property calculation? Q1->Q2 No P1 Protocol: NEMD Use itdmet=8/9 with tregime.in file to define heat zones. Q1->P1 Yes Q3 Does the protocol require a specific temperature profile? Q2->Q3 Equilibration P3 Protocol: Production MD Use Berendsen or Nose-Hoover with constant temperature. Damping: ~100 fs. Q2->P3 Property Calculation P2 Protocol: Simulated Annealing Use Berendsen with multiple Temperature and Duration periods. Damping: ~100 fs. Q3->P2 Yes (e.g., annealing) Q3->P3 No (constant T)

The Scientist's Toolkit: Research Reagent Solutions

This table details the essential computational "reagents" and their functions for setting up and executing ReaxFF MD simulations with proper temperature control.

Table 2: Essential Computational Materials for ReaxFF Thermostat Simulations

Item Name Function / Role in Simulation
Berendsen Thermostat A weak-coupling algorithm that efficiently scales velocities to maintain the system temperature, ideal for equilibration and many production runs [4].
Nose-Hoover Chain (NHC) Thermostat A deterministic algorithm that generates a correct canonical ensemble (NVT), preferred for rigorous sampling of equilibrium properties [42].
tregime.in File An input file that defines spatial zones and their respective thermostat properties, mandatory for NEMD simulations of thermal conductivity [42].
Damping Constant (Ï„) A key parameter (in fs) controlling the relaxation time of the thermostat; it determines how aggressively the thermostat corrects deviations from the target temperature [4].
AMSinput GUI The graphical user interface for the Amsterdam Modeling Suite (AMS) used to set up ReaxFF calculations, including task, force field, and thermostat parameters [4].
AMSmovie A visualization and analysis tool within AMS used to monitor simulation progress, plot properties like temperature and MSD, and analyze trajectories post-simulation [4].

Reparameterization Protocols for Accurate Solid-Phase Transport

The accurate simulation of solid-phase ion transport is a cornerstone in the development of next-generation energy storage and materials science. Reactive force field (ReaxFF) molecular dynamics (MD) has emerged as a powerful technique to model complex chemical environments where reactivity and transport phenomena are intricately linked. However, the standard parameterizations of ReaxFF often fail to correctly capture key properties of solid phases, particularly inorganic components of functional materials like those found in lithium-ion batteries (LIBs). This necessitates specialized reparameterization protocols to enhance the force field's accuracy for predicting solid-phase properties, especially ion diffusivity [8].

The solid-electrolyte interphase (SEI), a critical component in LIBs, exemplifies this challenge. Its correct operation, performance, and safety are heavily influenced by inorganic salts such as Lithium Fluoride (LiF). Standard ReaxFF parameterizations, trained primarily on dissociation energies and reaction kinetics, often inadequately describe the aggregation and solid-phase transitions of these salts, leading to inaccurate predictions of their transport properties [8]. This application note details a robust, interactive reparameterization protocol to address these limitations, thereby enabling more reliable MD simulations of solid-phase transport in functional materials.

Core Reparameterization Protocol

Protocol Workflow

The following diagram illustrates the comprehensive, iterative workflow for the interactive reparameterization of ReaxFF parameters, designed to enhance the description of solid-phase materials.

G Start Start: Identify Solid-Phase Target (e.g., LiF) QM_Data Generate QM Training Set Start->QM_Data Initial_FF Select Initial ReaxFF Parameter Set QM_Data->Initial_FF MD_Sim Perform MD Simulations Initial_FF->MD_Sim Property_Calc Calculate Key Properties (Diffusivity, Lattice Params) MD_Sim->Property_Calc Compare Compare with Reference Data Property_Calc->Compare Convergence Convergence Achieved? Compare->Convergence No / Insufficient Fit Update Update Parameters via Optimization Algorithm Convergence->Update No Final_FF Final Optimized Force Field Convergence->Final_FF Yes Update->MD_Sim Iterative Loop Validation Independent Validation Final_FF->Validation

Detailed Methodological Steps

Step 1: Target Identification and Training Set Curation The protocol begins by identifying the specific solid-phase material and property requiring improvement. For instance, to enhance the description of LiF in the SEI, the training set must be augmented with data that captures its solid-state nature. This includes [8]:

  • Crystal structure properties (lattice parameters, equations of state).
  • Elastic constants and surface energies.
  • Energy barriers for ion migration within the solid lattice. The training set should be constructed using high-fidelity quantum mechanical (QM) calculations, such as Density Functional Theory (DFT). Relying solely on data from isolated molecules or reaction dissociation energies is insufficient for capturing solid-phase behavior.

Step 2: Selection of an Optimization Algorithm The core of reparameterization is minimizing the error between ReaxFF-predicted and QM/experimental reference values. This is a challenging global optimization problem. While the sequential one-parameter parabolic extrapolation (SOPPE) method is common, it is prone to becoming trapped in local minima [43]. Recommended advanced algorithms include:

  • Improved Meta-heuristic Algorithms (IMHA): Combines Particle Swarm Optimization (PSO) with Latin Hypercube Design (LHD) for initial swarm generation and backtracking search strategies to escape local optima [43].
  • Automated Protocols: Leveraging Python libraries (e.g., ASE, PyMatgen, ParAMS) to orchestrate and automate the parameter optimization workflow, ensuring reproducibility and robustness [8].

Step 3: Iterative Validation and Force Field Assessment The optimized force field must be rigorously validated against a set of properties not included in the training set. Key validation tasks for solid-phase transport include [8]:

  • Equilibration MD Simulations: Ensuring the force field maintains the correct crystal structure at operational temperatures.
  • Diffusion Coefficient Calculation: Using Mean Squared Displacement (MSD) analysis on production MD trajectories to evaluate lithium ion diffusivity.
  • The optimized ReaxFF should recover the solid nature of the material and demonstrate a marked improvement in transport property prediction, such as a two-order-of-magnitude better prediction of Li⁺ diffusivity in LiF at room temperature [8].

Experimental Validation and Data Presentation

Key Validation Metrics

The success of the reparameterization protocol is quantitatively assessed by comparing key material properties before and after optimization. The table below summarizes typical validation metrics for an inorganic salt like LiF.

Table 1: Key Validation Metrics for Reparameterized ReaxFF (Example: LiF System)

Property Category Specific Metric Standard ReaxFF Reparameterized ReaxFF Target (QM/Experiment)
Crystal Structure Lattice Constant (Ã…) Incorrect / Unstable ~4.02 Ã… ~4.02 Ã… [8]
Density (g/cm³) Drifts from stable solid Stable solid density Matches reference
Mass Transport Li⁺ Diffusivity at 300 K (cm²/s) Overestimated by ~10² ~10⁻¹⁵ cm²/s ~10⁻¹⁵ cm²/s [8]
Mechanical Properties Elastic Constants (C₁₁, C₁₂, C₄₄) Incorrect relationship Matches experimental relationship Matches experiment [43]
Surface Properties Surface Energy (J/m²) Often underestimated Within 10% of DFT values DFT/Experimental values [43]
Protocol for Calculating Diffusion Coefficients

A critical step in validating the reparameterized force field is the accurate calculation of ion diffusion coefficients from MD trajectories. The following workflow is recommended for this purpose.

G A Input: Optimized Structure B Equilibration MD (NVT/NPT Ensemble) A->B C Production MD Run (High-Temperature possible) B->C D C->D E MSD Calculation D->E F VACF Calculation D->F G Linear Fit to MSD (D = slope/6) E->G H Integrate VACF (D = ∫VACF dt / 3) F->H I Output: Diffusion Coefficient (D) G->I H->I

Detailed Methodology [4]:

  • System Preparation and Equilibration:

    • Begin with an optimized geometry of the solid structure (e.g., Liâ‚€.â‚„S, LiF).
    • Perform an equilibration MD simulation in the NVT or NPT ensemble at the target temperature to stabilize the system's temperature and density.

  • Production MD Simulation:

    • Run a sufficiently long MD simulation (e.g., 100,000+ steps) to collect statistical data.
    • Use a time step of 0.25 fs and a thermostat (e.g., Berendsen) to maintain temperature.
    • Save the atomic positions and velocities frequently (e.g., every 5-10 steps) to generate a trajectory file.

  • Diffusion Coefficient Analysis via Mean Squared Displacement (MSD):

    • From the trajectory, calculate the MSD for the diffusing species (e.g., Li ions) using the formula: ( MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle )
    • Perform a linear regression on the MSD curve over a time region where it exhibits linear behavior. The diffusion coefficient ( D ) is obtained from the slope: ( D = \frac{\text{slope}(MSD)}{6} ) (for 3-dimensional diffusion).
    • Note: For solids with very low diffusivity at room temperature, calculating ( D ) directly may require impractically long simulations. In such cases, simulations are run at elevated temperatures, and the results are extrapolated to room temperature using the Arrhenius equation [4] [19].

  • Alternative Method: Velocity Autocorrelation Function (VACF):

    • As an alternative, the diffusion coefficient can be determined by integrating the Velocity Autocorrelation Function: ( D = \frac{1}{3} \int{0}^{t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \, dt )
    • This method requires a higher sampling frequency (smaller interval between saved velocities) in the trajectory.

Successful implementation of reparameterization protocols and subsequent MD simulations requires a suite of software tools and computational models.

Table 2: Essential Research Reagents and Computational Tools

Tool Name / Type Primary Function Key Features / Relevance
ReaxFF Reactive Force Field Engine Bond-order dependent potential for modeling chemical reactions; the core engine for MD simulations [8].
Python Ecosystem (ASE, PyMatgen, ParAMS) Reparameterization Automation Libraries for orchestrating atomistic simulations, managing parameter optimization, and automating workflows [8].
DFT Software (e.g., VASP, Quantum ESPRESSO) Training Data Generation Provides high-fidelity reference data (energies, structures, barriers) for the parameterization training set [8] [44].
AMS-ReaxFF Integrated MD Simulation Platform GUI and engine for setting up and running ReaxFF simulations, including diffusion coefficient calculations [4] [19].
Meta-heuristic Optimization Algorithms (e.g., IMHA, PSO) Force Field Parameter Optimization Advanced algorithms for navigating complex, high-dimensional parameter spaces to find global minima [43].

The interactive reparameterization protocol outlined herein provides a robust framework for enhancing the capability of ReaxFF to model solid-phase transport with high accuracy. By focusing on a targeted training set that includes solid-state properties and employing advanced global optimization algorithms, researchers can overcome the limitations of standard force fields. This approach, validated through rigorous calculation of properties like ion diffusivity, is indispensable for advancing computational studies in fields ranging from battery technology to material science, enabling more predictive and reliable molecular dynamics simulations.

Identifying and Resolving Non-Linear MSD Behavior

In molecular dynamics (MD) simulations, the mean squared displacement (MSD) is a fundamental metric for quantifying atomic diffusion. The diffusion coefficient (D) is directly derived from the slope of the MSD over time via the relationship ( D = \frac{\text{slope(MSD)}}{6} ) for 3-dimensional diffusion [4]. A linear MSD profile indicates normal, unconstrained diffusion, while non-linear behavior often signals underlying issues with the simulation setup, system properties, or analysis methodology. For researchers using reactive force fields (ReaxFF) to study diffusion in complex systems like lithium-ion batteries [4] [8], identifying and resolving the root causes of non-linear MSD is crucial for obtaining accurate and physically meaningful diffusion coefficients. This Application Note provides a structured framework for diagnosing and correcting non-linear MSD behavior within the context of ReaxFF MD simulations.

Understanding MSD and Its Significance

The MSD calculates the average square of the distance an atom travels over time, providing a direct window into dynamic behavior. In a typical MSD analysis, the trajectory is divided into multiple time origins, and the displacement is calculated for various time intervals from each origin. This averaging is essential for obtaining good statistics. The key quantitative relationship is:

[ MSD(t) = \langle [\textbf{r}(0) - \textbf{r}(t)]^2 \rangle ]

[ D = \frac{\text{slope(MSD)}}{6} ]

Where (\textbf{r}(0)) and (\textbf{r}(t)) are the atomic positions at time zero and time t, respectively, and the angle brackets represent the ensemble average [4]. In an ideal diffusive system, the MSD plot should be a straight line, confirming that the particles are undergoing random Brownian motion. The slope of this line, divided by the dimensionality factor (6 for 3D diffusion), yields the diffusion coefficient. Non-linearity in the MSD plot indicates a deviation from this ideal behavior, requiring systematic investigation.

A Diagnostic Framework for Non-Linear MSD

Non-linear MSD profiles can manifest in different forms, each suggesting distinct underlying causes. The following table categorizes common patterns, their interpretations, and recommended diagnostic actions.

Table 1: Patterns of Non-Linear MSD Behavior and Initial Diagnostics

MSD Pattern Physical Interpretation Diagnostic Checks
Initial Curvature (Sub-diffusion) Restricted motion, confinement, or incomplete equilibration. Check equilibration phase (e.g., volume stability). Analyze system density and potential energy time series. Inspect the simulation box for artificial constraints.
Plateauing or Saturation Limited volume for diffusion, indicative of finite-size effects or trapping. Verify system size (use larger supercells for bulk diffusion) [4]. Check for frozen atoms or rigid parts of the system. Calculate MSD for different atomic subsets.
Erratic Oscillations Poor statistics, trajectory too short, or insufficient sampling. Extend the simulation time to improve averaging. Check if the MSD time (t) is less than ~1/5 of total trajectory length. Verify sampling frequency is appropriate.
Upward Curvature (Super-diffusion) Directed flow, unphysical forces, or system drift. Check for momentum conservation (remove center-of-mass motion). Analyze temperature and pressure stability throughout the trajectory. Inspect for unphysical interactions in the force field.
The Diagnostic Workflow

The following diagram outlines a systematic workflow for diagnosing the root cause of non-linear MSD behavior, integrating the checks outlined in Table 1.

Start Observe Non-Linear MSD P1 Check Equilibration Status Start->P1 P2 Verify Simulation Length and Sampling P1->P2 Equilibration OK? P3 Assess System Size for Finite-Size Effects P2->P3 Statistics OK? P4 Inspect Force Field and System Composition P3->P4 Size OK? P5 Identify Root Cause P4->P5

Figure 1: A systematic diagnostic workflow for non-linear MSD behavior.

Protocols for Resolving Non-Linear MSD

Ensuring Proper System Equilibration

Inadequate equilibration is a primary cause of initial MSD curvature. The system must reach a state of thermodynamic equilibrium before the production MD run used for diffusion analysis.

Protocol: Simulated Annealing for Amorphous Systems For complex systems like lithiated sulfur cathodes, a simulated annealing protocol can generate well-equilibrated amorphous structures [4].

  • Initial Optimization: Start with a geometry-optimized structure, including lattice relaxation [4].
  • Annealing MD: Perform an MD simulation with a tailored temperature profile:
    • Step 1 (0-5,000 steps): Hold at 300 K.
    • Step 2 (5,000-25,000 steps): Linearly heat from 300 K to 1600 K.
    • Step 3 (25,000-30,000 steps): Rapidly cool from 1600 K back to 300 K [4].
  • Re-equilibration: Conduct a final geometry optimization (with lattice relaxation) on the annealed structure to obtain a stable starting configuration for production MD.
Optimizing Production MD Settings

The parameters of the production MD run critically impact the quality of the diffusion data.

Protocol: Setting up a Robust Production MD Simulation [4]

  • Simulation Length: Run a minimum of 100,000-200,000 steps for production. The MSD analysis time (t) should not exceed ~20% of the total trajectory length to maintain good statistics.
  • Thermostat: Use a thermostat like Berendsen with a damping constant of 100 fs to maintain a stable temperature (e.g., 1600 K for high-temperature studies).
  • Sampling Frequency: Set the Sample frequency to write atomic positions and velocities every 5-10 steps. A higher frequency is needed for VACF analysis, while a lower frequency is sufficient for MSD analysis and results in smaller trajectory files [4].
  • Time Step: A time step of 0.25 fs is typical for ReaxFF. Therefore, a Sample frequency of 5 results in coordinates saved every 1.25 fs.
Addressing Finite-Size Effects and Force Field Limitations

The calculated diffusion coefficient can be artificially low if the simulation cell is too small, as atoms quickly feel the periodic images of themselves.

Resolution: To mitigate finite-size effects, perform simulations for progressively larger supercells and extrapolate the calculated diffusion coefficients to the "infinite supercell" limit [4].

Furthermore, the force field itself may be a source of inaccuracy. Standard ReaxFF parameterizations may not accurately capture the solid nature of certain components, such as lithium fluoride (LiF) in battery anodes, leading to erroneous lithium diffusivity. In such cases, a specialized reparameterization protocol, leveraging Python libraries (ASE, PyMatgen, ParAMS) to refine parameters against ab initio data, can dramatically improve accuracy, as demonstrated by a two-order-of-magnitude improvement in LiF diffusivity prediction at room temperature [8].

Practical Implementation and Analysis in AMS

The Amsterdam Modeling Suite (AMS) provides integrated tools for running ReaxFF MD and analyzing the results. This section details the hands-on steps.

The Scientist's Toolkit: Essential Research Reagents

Table 2: Key Software Tools and Their Functions in ReaxFF MD Workflows

Tool Name Type Primary Function in Diffusion Studies
AMSinput GUI Software Module Setting up MD simulations (task, force field, thermostat details) [4].
ReaxFF Force Field Engine Performing reactive MD simulations with optimized parameters for specific elements [5] [8].
AMSmovie GUI Analysis Tool Visualizing trajectories and calculating key properties like MSD and VACF [4].
ParAMS Parameterization Tool Building and refining new ReaxFF parameter sets to improve accuracy for specific materials [8].
ASE (Atomic Simulation Environment) Python Library Scripting, automating, and orchestrating atomistic simulations [8].
PyMatgen (Python Materials Genomics) Python Library Manipulating crystal structures, analyzing materials, and handling data [8].
Step-by-Step MSD Analysis Protocol in AMSmovie

After running the production MD, follow these steps to analyze the MSD:

  • Open the trajectory in AMSmovie.
  • Navigate to MD Properties → MSD.
  • Set the Steps range to exclude the equilibration period (e.g., 2000 - 22001).
  • Set Atoms to the diffusing species of interest (e.g., Li).
  • Set Max MSD Frame to an appropriate value (e.g., 5000, which corresponds to 5000 * 1.25 fs = 6250 fs).
  • Click Generate MSD [4].

The tool will plot the MSD and a derived D(t) curve. A reliable diffusion coefficient is the value where the D(t) curve plateaus. If it does not plateau, the simulation likely requires more time.

An Alternative Method: Velocity Autocorrelation Function (VACF)

The VACF provides an independent method to calculate the diffusion coefficient, defined as: [ D = \frac{1}{3} \int{t=0}^{t=t{max}} \langle \textbf{v}(0) \cdot \textbf{v}(t) \rangle \rm{d}t ] Protocol for VACF analysis in AMSmovie [4]:

  • In AMSmovie, go to MD Properties → Autocorrelation function.
  • Set Steps, Atoms, and Max ACF Step as for the MSD analysis.
  • Select Property → Diffusion Coefficient (D).
  • Click Generate ACF. The bottom plot shows the diffusion coefficient from VACF; it should converge to a horizontal line for a valid result. Agreement between MSD and VACF results increases confidence in the calculated D.

Advanced Strategy: Extrapolation from High Temperatures

At lower temperatures (e.g., 300 K), diffusion is slow, and obtaining a linear MSD requires impractically long simulation times. A solution is to use an Arrhenius extrapolation from higher temperatures.

Protocol: Arrhenius Extrapolation for Diffusion Coefficients [4]

  • Calculate D at High T: Perform production MD simulations and calculate D for at least four different elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K).
  • Create an Arrhenius Plot: Plot the natural logarithm of the diffusion coefficient, (\ln{D(T)}), against the inverse temperature, (1/T).
  • Linear Fit: Fit the data points to the Arrhenius equation: [ \ln{D(T)} = \ln{D0} - \frac{Ea}{k{B}}\cdot\frac{1}{T} ] where (D0) is the pre-exponential factor and (E_a) is the activation energy.
  • Extrapolate: Use the fitted line to extrapolate the value of (D(T)) at the desired lower temperature (e.g., 300 K). This provides an upper-bound estimate for the diffusion coefficient.

The workflow for this advanced approach, which integrates multiple simulations and analysis steps, is summarized below.

Start Run MD at Multiple High T A Calculate D at each T (via MSD or VACF) Start->A B Plot ln(D) vs. 1/T (Arrhenius Plot) A->B C Perform Linear Fit B->C D Extrapolate D to Lower T C->D

Figure 2: Workflow for extrapolating diffusion coefficients to lower temperatures using the Arrhenius relation.

Non-linear MSD behavior in ReaxFF MD simulations is a common challenge but can be systematically diagnosed and resolved. Key strategies include ensuring thorough system equilibration, conducting sufficiently long production runs, validating results against the VACF method, and understanding the limitations imposed by system size and force field parameterization. For slow diffusion systems, Arrhenius extrapolation from high-temperature simulations provides a practical solution for estimating room-temperature diffusivity. By adhering to these detailed protocols, researchers can enhance the reliability of their diffusion coefficient calculations, thereby contributing to more accurate computational studies of material transport properties.

Validating Results and Extending Applications Across Temperature Ranges

Within the framework of ReaxFF molecular dynamics, calculating the self-diffusion coefficient ((D)) is fundamental for understanding atomic and molecular transport in materials, from battery electrodes to catalysts. Two principal experimental protocols exist for extracting this property from an MD trajectory: the Mean Squared Displacement (MSD) method and the Velocity Autocorrelation Function (VACF) method. While theoretically equivalent in the long-time limit, their practical application involves distinct computational procedures and potential pitfalls. This Application Note provides a detailed protocol for performing these analyses and, crucially, cross-validating the results to ensure computational reliability and accuracy. Cross-validation acts as a critical internal consistency check, bolstering confidence in the reported diffusion coefficients [4].

Theoretical Foundation

The self-diffusion coefficient describes the rate at which a particle randomly travels through a material. The two methods to compute it are derived from statistical mechanics.

2.1 The Mean Squared Displacement (MSD) Method The MSD approach relies on the Einstein relation, which connects the diffusion coefficient to the slope of the mean squared displacement of particles over time. For 3-dimensional diffusion, the relationship is given by:

[D = \frac{1}{6} \lim_{t \to \infty} \frac{d}{dt} \text{MSD}(t)]

where the MSD is defined as: [\text{MSD}(t) = \left\langle \left| \vec{r}i(t) - \vec{r}i(0) \right|^2 \right\rangle] Here, (\vec{r}_i(t)) is the position of particle (i) at time (t), and the angle brackets (\langle \cdots \rangle) represent an ensemble average over all particles of the same type and over multiple time origins [4] [45]. The factor of 6 accounts for the 3 dimensions of space (2 dimensions would require a factor of 4). In practice, (D) is obtained by performing a linear regression on the linear portion of the MSD(t) versus time curve.

2.2 The Velocity Autocorrelation Function (VACF) Method The Green-Kubo formalism provides an alternative route to the diffusion coefficient via the integration of the Velocity Autocorrelation Function:

[D = \frac{1}{3} \int{0}^{\infty} \langle \vec{v}i(0) \cdot \vec{v}_i(t) \rangle \, dt]

Here, (\langle \vec{v}i(0) \cdot \vec{v}i(t) \rangle) is the VACF, which measures how a particle's velocity at one time is correlated with its velocity at a later time [4] [46]. The VACF typically decays from a positive value at (t=0) and may oscillate into negative values, indicating back-scattering events. The diffusion coefficient is proportional to the total area under the VACF curve.

Experimental Protocols

Prerequisites and Simulation Setup

3.1.1 ReaxFF Force Field Selection and System Preparation Begin by selecting an appropriate ReaxFF force field parameterized for the elements and interactions in your system (e.g., LiS.ff for lithium-sulfur systems [4]). Construct the initial atomic structure, which may involve importing a crystal structure, energy minimization, and equilibration via molecular dynamics in the NVT or NPT ensemble to stabilize temperature and density.

3.1.2 Production MD Run for Diffusion Analysis

  • Task: Molecular Dynamics.
  • Force Field: Your selected ReaxFF force field.
  • Ensemble: NVT for strict temperature control.
  • Thermostat: Berendsen or Nose-Hoover with a damping constant of 100 fs.
  • Temperature: Set to the target temperature (e.g., 1600 K for high-temperature studies [4]).
  • Number of Steps: A sufficiently long production run (e.g., >100,000 steps) is critical for gathering adequate statistics.
  • Time Step: 0.25-1.0 fs, as dictated by ReaxFF requirements.
  • Sample Frequency: A key parameter. For MSD analysis, a frequency of 5-10 steps is often sufficient. For VACF analysis, a higher sampling frequency (e.g., every step) is recommended to accurately capture velocity correlations [4].
  • Trajectory Output: Ensure atomic positions and velocities are written to the trajectory file. The velocities are essential for the VACF calculation.
  • Critical Consideration - Unwrapped Coordinates: The trajectory must be saved in unwrapped coordinates or have periodic boundary corrections applied during analysis. Using wrapped coordinates, where atoms are artificially moved back into the primary simulation cell, will severely corrupt the MSD calculation [45]. Tools like gmx trjconv in GROMACS with the -pbc nojump flag can be used for this purpose.

Protocol A: Calculating D via Mean Squared Displacement

This protocol outlines the steps for calculating the diffusion coefficient using the MSD method, which is generally more straightforward and is the recommended initial approach [4].

Step 1: Compute the MSD Load the production trajectory into an analysis tool (e.g., AMSmovie [4], MDAnalysis [45], GROMACS gmx msd [47]).

  • Atom Selection: Specify the atom type for analysis (e.g., Li for lithium ions).
  • Averaging: The analysis software should automatically perform an ensemble average over all selected atoms and a time average over multiple time origins to improve statistics.
  • MSD Type: Select a 3-dimensional MSD (xyz).

Step 2: Identify the Linear Diffusion Regime Plot the MSD as a function of time. The plot is often divided into three regions:

  • A ballistic regime at short times, where MSD (\propto t^2).
  • A linear diffusion regime at intermediate times, where MSD (\propto t).
  • A plateau or noisy regime at long times due to finite-size effects and poor averaging. Visually inspect the plot or use a log-log plot (where the linear regime has a slope of 1) to identify the start and end of the linear regime [45].

Step 3: Perform Linear Regression On the identified linear segment of the MSD plot (e.g., from (t{\text{start}}) to (t{\text{end}})), perform a least-squares linear fit of the form: [ \text{MSD}(t) = m \cdot t + c ] where (m) is the slope.

Step 4: Calculate the Diffusion Coefficient The diffusion coefficient is calculated from the slope: [ D_{\text{MSD}} = \frac{m}{6} ] The factor of 6 is for 3D diffusion. For 2D and 1D, use factors of 4 and 2, respectively.

Protocol B: Calculating D via Velocity Autocorrelation Function

This protocol is used to calculate the diffusion coefficient via the VACF, serving as a complementary method for validation.

Step 1: Compute the VACF Load the production trajectory (with velocity information) into an analysis tool (e.g., AMSmovie [4], LAMMPS compute vacf [46]).

  • Atom Selection: Specify the atom type (e.g., Li).
  • The tool will compute the normalized VACF, (\langle \vec{v}i(0) \cdot \vec{v}i(t) \rangle / \langle \vec{v}i(0) \cdot \vec{v}i(0) \rangle).

Step 2: Integrate the VACF The analysis tool will numerically integrate the VACF over time to produce a running integral: [ I(t) = \frac{1}{3} \int{0}^{t} \langle \vec{v}i(0) \cdot \vec{v}_i(t') \rangle \, dt' ] This integral (I(t)) is an estimate of (D(t)).

Step 3: Identify the Converged Value Plot the running integral (I(t)) as a function of time. For a valid calculation, this curve will plateau to a constant value at long times. The value at which this curve converges is the diffusion coefficient, (D_{\text{VACF}}) [4].

Results and Data Analysis

Data Presentation and Cross-Validation

The core of cross-method validation is the direct comparison of (D{\text{MSD}}) and (D{\text{VACF}}). The results from both analyses should be compiled into a summary table for evaluation.

Table 1: Sample Comparison of Diffusion Coefficients from MSD and VACF Methods for Li Ions in a Model System at 1600 K

Method Principle Calculated D (10⁻⁸ m²/s) Linearity/Convergence Quality
MSD Slope of (\langle \Delta r^2 \rangle) vs (t) 3.09 [4] Good linear fit from 2-6 ps
VACF Integral of (\langle \vec{v}(0)\cdot\vec{v}(t) \rangle) 3.02 [4] Clear plateau after ~5 ps

4.1.1 Interpretation of Comparative Data As shown in Table 1, the diffusion coefficients calculated from MSD and VACF are in excellent agreement (3.09 vs. 3.02 ×10⁻⁸ m²/s), providing strong cross-validation for the simulation and analysis. A difference of less than 5% is typically considered excellent agreement. Significant discrepancies (e.g., >20%) indicate a problem in the simulation or analysis setup.

Troubleshooting Guide

Table 2: Troubleshooting Common Discrepancies Between MSD and VACF Results

Observation Potential Cause Solution
DMSD >> DVACF Trajectory uses wrapped coordinates for MSD calculation. Re-analyze using unwrapped coordinates [45].
DVACF >> DMSD Poor VACF statistics; integration not converged. Run a longer simulation to improve sampling.
Both D values are low/noisy Simulation time is too short, not reaching diffusive regime. Increase the number of production MD steps.
MSD curve is non-linear System is not at equilibrium or is a non-diffusive solid. Check equilibration and ensure the simulation temperature is correct.
VACF integral fails to plateau Insufficient sampling or correlation time too long. Use a longer trajectory or check for system anomalies.

The Scientist's Toolkit

Table 3: Essential Research Reagent Solutions for ReaxFF Diffusion Studies

Tool / Reagent Function in Protocol
ReaxFF Force Field (e.g., LiS.ff) Provides the potential energy function describing atomic interactions. The quality of the force field is the primary determinant of simulation accuracy [4].
Equilibrated Molecular System The starting configuration of atoms (e.g., Li0.4S) after energy minimization and NVT/NPT equilibration, representing a stable, thermalized system [4].
Unwrapped Trajectory File The output of the production MD run, containing atomic positions and velocities without periodic boundary jumps. This is the fundamental "reagent" for all diffusion analysis [45].
MD Analysis Software (AMS, MDAnalysis, GROMACS, LAMMPS) Software packages used to compute ensemble averages, MSD, VACF, and perform linear regression or integration to extract the final diffusion coefficient [4] [45] [46].

Visual Guide to Workflow and Cross-Validation

The following diagram illustrates the overall workflow for calculating and cross-validating diffusion coefficients, integrating both the MSD and VACF protocols.

Figure 1: Integrated workflow for MSD/VACF cross-validation.

The logical relationship between the two methods and the critical cross-validation step is further detailed in the following diagram.

Figure 2: Logical relationship and validation checkpoint between the two theoretical methods.

This Application Note provides a rigorous protocol for computing diffusion coefficients in ReaxFF molecular dynamics simulations using the complementary MSD and VACF methods. The presented workflows, troubleshooting guide, and data comparison tables offer researchers a clear pathway to obtain reliable results. The practice of cross-validating results between these two independent methods is not merely a best practice but a necessity for generating robust, publication-quality data. It effectively mitigates the risk of errors stemming from trajectory handling, statistical sampling, or analysis parameters, thereby strengthening the scientific conclusions drawn from the simulations.

The Arrhenius plot is a powerful tool for extrapolating reaction rates or diffusion coefficients from experimentally accessible conditions to target, often lower-temperature, operational conditions. Within the context of ReaxFF molecular dynamics (MD) simulations, this methodology is essential for predicting long-term material behavior, such as ion diffusion in battery materials, from short-term, high-temperature simulations. This protocol details the application of Arrhenius methodology to extrapolate diffusion coefficients, providing a bridge between atomic-scale simulations and macroscale experimental predictions. The core principle relies on the Arrhenius equation, which describes the temperature dependence of the rate constant, k (or diffusion coefficient, D), and allows for reliable extrapolation provided the underlying mechanism remains unchanged [48] [49] [50].

Theoretical Foundation

The methodology is grounded in the Arrhenius equation, which can be expressed in two primary forms.

The Arrhenius Equation

The fundamental Arrhenius equation is: [ k = A \exp\left(\frac{-E_a}{RT}\right) ] where:

  • ( k ) is the rate constant (or the diffusion coefficient, ( D ))
  • ( A ) is the pre-exponential factor (or frequency factor)
  • ( E_a ) is the activation energy (in J/mol)
  • ( R ) is the universal gas constant (8.314 J/mol·K)
  • ( T ) is the absolute temperature (in K) [48] [49]

For diffusion coefficients, the equation is written analogously as: [ D(T) = D0 \exp\left(\frac{-Ea}{kB T}\right) ] where ( kB ) is the Boltzmann constant, used when activation energy is expressed per molecule [4].

Linearized Form for Plotting

To create an Arrhenius plot, the equation is transformed into a linear form: [ \ln(k) = \ln(A) - \frac{E_a}{R} \left(\frac{1}{T}\right) ] This has the form of a straight line, ( y = mx + c ), where:

  • ( y = \ln(k) )
  • ( x = 1/T )
  • Slope ( m = -E_a/R )
  • Y-intercept ( c = \ln(A) ) [48] [49]

This linear relationship is the foundation of the extrapolation methodology.

Experimental Protocol: Diffusion Coefficient from ReaxFF MD

This protocol outlines the calculation of diffusion coefficients for ionic species (e.g., Li⁺) in a material like Li₀.₄S at multiple temperatures, as required for constructing an Arrhenius plot [4].

System Preparation and Equilibration

  • Import/Generate the Structure: Begin with a crystal structure (e.g., a CIF file). For a system like Liâ‚€.â‚„S, insert lithium atoms randomly into the sulfur matrix or use Grand Canonical Monte Carlo (GCMC) for a more accurate structure [4].
  • Geometry Optimization: Perform a geometry optimization calculation, including lattice relaxation, using the ReaxFF force field to obtain a stable, low-energy starting structure [4].
  • Simulated Annealing (for Amorphous Systems): To generate an amorphous structure:
    • Run a molecular dynamics simulation with a specific temperature profile.
    • Step 1: Hold at 300 K for 5,000 steps.
    • Step 2: Heat from 300 K to 1600 K over 20,000 steps.
    • Step 3: Cool down from 1600 K to 300 K over 5,000 steps.
    • This process helps in creating a realistic amorphous material structure [4].
  • Final Optimization: Relax the geometry of the resulting annealed structure with another geometry optimization, including lattice relaxation [4].

Production MD and Diffusion Coefficient Calculation

  • Set Up MD Simulation: Configure a production MD simulation at a specific temperature (e.g., 1600 K).
    • Task: Molecular Dynamics.
    • Number of Steps: Typically 100,000-110,000 steps (including an initial equilibration phase).
    • Sample Frequency: Set to 5-10 to record atomic positions and velocities periodically. The time between trajectory points is sample_frequency * time_step [4].
  • Run at Multiple Temperatures: Repeat the production MD simulation for at least four different temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) to obtain sufficient data for a reliable Arrhenius plot [4].
  • Calculate Diffusion Coefficient (D): After the simulation, analyze the trajectory to compute D using one of two primary methods:
    • A. Mean Squared Displacement (MSD) - Recommended:
      • Calculate the MSD: ( MSD(t) = \langle [\mathbf{r}(0) - \mathbf{r}(t)]^2 \rangle )
      • The diffusion coefficient is derived from the slope of the MSD vs. time plot: ( D = \frac{\text{slope(MSD)}}{6} ) for 3-dimensional diffusion [4].
      • Ensure the MSD plot is linear; a non-linear plot indicates the need for a longer simulation to gather better statistics.
    • B. Velocity Autocorrelation Function (VACF):
      • Calculate the VACF and integrate it: ( D = \frac{1}{3} \int{0}^{t{\text{max}}} \langle \mathbf{v}(0) \cdot \mathbf{v}(t) \rangle dt ) [4].
      • The resulting plot of the integral should converge to a horizontal line for large enough times, indicating the value of D.

Workflow Visualization

The following diagram illustrates the complete workflow from system preparation to diffusion coefficient extrapolation.

start Start: System Preparation opt Geometry Optimization with Lattice Relaxation start->opt anneal Simulated Annealing (Heating & Cooling) opt->anneal md Production MD Run at Temperature T anneal->md calc Calculate Diffusion Coefficient D(T) md->calc repeat Repeat for Multiple Temperatures calc->repeat arrhenius Construct Arrhenius Plot ln(D) vs. 1/T repeat->arrhenius fit Linear Fit to Determine Slope arrhenius->fit extr Extrapolate D to Target Temperature fit->extr

Constructing the Arrhenius Plot and Extrapolation

  • Tabulate Data: Compile the calculated diffusion coefficients and their corresponding temperatures into a table.
  • Transform Data: Calculate the natural logarithm of each diffusion coefficient, ln(D), and the inverse of each absolute temperature, 1/T.
  • Create the Arrhenius Plot:
    • Plot ln(D) on the y-axis against 1/T on the x-axis.
    • The data points should align in a roughly linear fashion if the diffusion mechanism is consistent across the temperature range [48] [49].
  • Perform Linear Regression: Fit a straight line to the data points. The equation of the line will be: ( \ln(D) = \ln(D0) - \frac{Ea}{R} \cdot \frac{1}{T} ) [4] [49].
  • Extract Parameters:
    • Activation Energy ((Ea)): Calculate from the slope: ( Ea = - \text{slope} \times R ).
    • Pre-exponential Factor ((D0)): Calculate from the y-intercept: ( D0 = \exp(\text{intercept}) ).
  • Extrapolate: Use the fitted linear equation to calculate the diffusion coefficient ((D{\text{target}})) at your target temperature ((T{\text{target}})) by plugging ( 1/T_{\text{target}} ) into the equation.

Quantitative Data Presentation

Table 1: Example Data Structure for Arrhenius Plot Construction

Temperature (T) [K] 1/T [K⁻¹] Diffusion Coefficient (D) [m²/s] ln(D) Method
1600 0.000625 3.09 × 10⁻⁸ -17.29 MSD
1600 0.000625 3.02 × 10⁻⁸ -17.32 VACF
1200 0.000833 [Value] [Value] MSD
800 0.001250 [Value] [Value] MSD
600 0.001667 [Value] [Value] MSD

Table 2: Key Parameters Derived from Arrhenius Plot Linear Fit

Parameter Symbol Value from Example Unit
Slope ( m ) -12,667 K
Activation Energy ( E_a ) 105.3 kJ/mol
Pre-exponential Factor ( D_0 ) 1.08 × 10¹⁰ m²/s
Correlation Coefficient ( R^2 ) >0.99 -

The Scientist's Toolkit: Research Reagent Solutions

Table 3: Essential Materials and Computational Tools

Item / Software Function / Description Application Note
ReaxFF Force Field A reactive force field enabling MD simulations of chemical reactions and bond formation/breaking. Critical for simulating diffusion in complex, reacting materials like lithiated sulfur cathodes [4].
AMS Software Package A comprehensive computational chemistry suite that includes the ReaxFF MD engine. Used for running geometry optimizations, simulated annealing, and production MD simulations [4].
Thermogravimetric Analysis (TGA) An experimental method to validate simulation results by measuring mass loss of volatile components. Can be used to determine an "average" diffusion coefficient of volatiles in polymer melts for comparison [51].
Pressure Decay Apparatus (PDA) An indirect experimental method to determine diffusion coefficients by measuring pressure drop in a closed cell. Serves as a validation method for diffusion coefficients obtained from other techniques like TGA or simulation [51].
Yttrium-Doped Zirconia A model ionic conducting oxide. Used in experimental validation of electrochemical methods for determining diffusion coefficients of mobile species [52].

Critical Assumptions and Limitations

  • Constant Mechanism: The core assumption is that the diffusion (or degradation) mechanism remains identical across the entire temperature range studied and extrapolated to. A change in mechanism, such as from vacancy migration to complex defect migration, will manifest as a break in the linearity of the Arrhenius plot, invalidating the extrapolation [52] [50].
  • Finite-Size Effects: The diffusion coefficient calculated from MD simulations can depend on the size of the simulation supercell. To mitigate this, simulations should be performed for progressively larger supercells, with the results extrapolated to the "infinite supercell" limit [4].
  • Statistical Reliability: The linear fit to the Arrhenius plot requires data from multiple temperatures (at least four are recommended). Short MD trajectories resulting in non-linear MSD plots will lead to poor estimates of D and unreliable extrapolation [4].

Benchmarking Against Ab Initio and Experimental Data

The Reactive Force Field (ReaxFF) molecular dynamics method serves as a crucial bridge between highly accurate but computationally expensive quantum mechanical (ab initio) methods and efficiently scalable but non-reactive classical molecular dynamics simulations [2]. By employing a bond-order formalism, ReaxFF enables the simulation of chemical reactions, including bond breaking and formation, in complex systems across extended timescales and larger sizes than are typically feasible with ab initio methods alone [2]. However, the reliability of ReaxFF predictions hinges entirely on rigorous validation against benchmark data. This application note provides detailed protocols and quantitative assessments for benchmarking ReaxFF molecular dynamics simulations, with a specific focus on calculating diffusion coefficients, ensuring their accuracy against ab initio and experimental reference data.

ReaxFF Methodology and Benchmarking Principle

Foundations of the ReaxFF Method

ReaxFF employs a bond-order formalism to describe reactive interactions, allowing for the dynamic formation and breaking of bonds during a simulation [2]. The total system energy is partitioned into several contributions [2]: ( E{system} = E{bond} + E{over} + E{angle} + E{tors} + E{vdWaals} + E{Coulomb} + E{Specific} )

Unlike traditional force fields with fixed connectivity, ReaxFF calculates bond order (( BO{ij} )) directly from interatomic distances (( r{ij} )) using an empirical formula that smoothly transitions between single, double, and triple bond character [2]: ( BO{ij} = BO{ij}^\sigma + BO{ij}^\pi + BO{ij}^{\pi\pi} = \exp \left[p{bo1}\left(\frac{r{ij}}{r0^\sigma}\right)^{p{bo2}}\right] + \exp \left[p{bo3}\left(\frac{r{ij}}{r0^\pi}\right)^{p{bo4}}\right] + \exp \left[p{bo5}\left(\frac{r{ij}}{r0^{\pi\pi}}\right)^{p{bo6}}\right] )

This approach, coupled with a charge equilibration method (e.g., EEM - Electronegativity Equalization Method) to handle atomic charges dynamically, allows ReaxFF to simulate complex chemical reactivity in multi-phase systems [53] [2].

The Benchmarking Workflow

The following diagram illustrates the iterative protocol for developing and validating a ReaxFF force field parameter set, which is critical for obtaining accurate diffusion properties.

G Start Start: Define System and Target Properties TS Create/Compile Training Set Start->TS Param Force Field Parameterization TS->Param MD Perform ReaxFF MD Simulation Param->MD Calc Calculate Diffusion Coefficient MD->Calc Benchmark Benchmark against Ab Initio & Exp. Data Calc->Benchmark Decision Agreement Adequate? Benchmark->Decision Decision->TS No End Validated Force Field Decision->End Yes

Quantitative Benchmarking Data

Benchmarking requires comparing ReaxFF output against reliable reference data. The following tables summarize key quantitative comparisons for diffusion coefficients and related properties from documented studies.

Table 1: Benchmarking ReaxFF for Geofluid (NaAlSi3O8-H2O) Systems [53]

Property System Condition ReaxFF Result Reference Data/Validation
Si Coordination 1000–3000 K, ~2 GPa Primarily 4-coordinated Consistent with ab initio and spectroscopic data
Al Coordination 1000–3000 K, ~2 GPa 3 to 6 coordinate Consistent with ab initio and spectroscopic data
Speciation Trend Increasing H2O content Q4/Q5 decrease, Q0 increases; Dominant: Q4→Q3→Q2→Q1→Q0 Matches ab initio (FPMD) trends [53]
Diffusivity/Viscosity 1000-3000 K, ~2 GPa Quantitative models as a function of water content and temperature Used to predict transport properties of hydrous silicate melts/fluids

Table 2: Benchmarking ReaxFF for Hydrogen Diffusion in Ruthenium [21]

System Structure Temperature Range Activation Energy (Ea) Diffusion Coefficient Pre-factor (D0) Validation Method
Pristine Ru crystal 600 - 1500 K 0.23 eV - ReaxFF MD vs. DFT barriers
Σ7 Tilt Grain Boundary 600 - 1500 K - - DFT training set
Σ7 Twist Grain Boundary 600 - 1500 K - - DFT training set

Table 3: Performance and Limitations of ReaxFF in Benchmarking Studies

Application Area Reported Strength Reported Challenge/Limitation Impact on Diffusion Prediction
Hydrogen Combustion [54] Capable of large-scale simulation of combustion systems Can fail quantitatively and qualitatively for specific reactive events Directly affects reaction rates and species transport
Li-ion Batteries (LiF) [55] Can be reparameterized to recover solid nature and improve mass transport properties Strong sensitivity to training set; challenges in interpolating potential energy surface Improved LiF ReaxFF increased Li+ diffusivity prediction accuracy by two orders of magnitude [55]
General ReaxFF Methodology [2] Good transferability across periodic table; bridges scale between QM and classical MD Trade-off of accuracy for computational expense; parameterization is system-specific Diffusion properties are highly sensitive to the quality and breadth of the training set

Detailed Experimental Protocols

Protocol 1: Benchmarking Diffusion in Supercritical Geofluids

This protocol outlines the procedure for simulating and validating the diffusion of species in a supercritical NaAlSi3O8-H2O fluid, as performed in a recent ReaxFF study [53].

  • 1. System Setup and Force Field Selection:

    • Model Construction: Construct a simulation cell containing the relevant number of Na, Al, Si, O, and H atoms to represent the desired composition (e.g., 5–80 wt% water).
    • Force Field: Employ a ReaxFF parameter set specifically developed and validated for earth materials (e.g., containing Si/Al/O/H/Na). The force field must be capable of handling silicate-water interactions and polarization effects [53] [2].

  • 2. Molecular Dynamics Simulation:

    • Equilibration: Run an initial simulation in the NpT (isothermal-isobaric) ensemble at the target pressure (e.g., ~2 GPa) and temperature (1000–3000 K) until the system density and energy stabilize. Use a thermostat (e.g., Nosé-Hoover) and barostat (e.g., Berendsen) with appropriate damping constants.
    • Production Run: Switch to an NVT (canonical) ensemble for the production run. Use a time step of 0.25–1.0 fs. The total simulation time must be long enough to observe sufficient particle displacement for a reliable diffusion calculation (typically hundreds of picoseconds to nanoseconds).

  • 3. Trajectory Analysis and Diffusion Calculation:

    • Mean-Squared Displacement (MSD): From the production trajectory, calculate the MSD for the atomic species of interest (e.g., Na, Si, O in H2O).
    • Einstein-Smoluchowski Relation: Calculate the diffusion coefficient (D) using the relation [21]: ( D = \frac{1}{2d} \lim_{t \to \infty} \frac{\partial \langle |r(t) - r(0)|^2 \rangle}{\partial t} ) where ( d ) is the dimensionality (3 for 3D diffusion), ( r(t) ) is the position at time ( t ), and the angle brackets denote an average over all atoms of the same type and time origins.

  • 4. Benchmarking and Validation:

    • Against Ab Initio: Compare the calculated diffusion coefficients, coordination numbers (e.g., Si being primarily 4-coordinated), and structural speciation (Qn species) with results from First-Principles Molecular Dynamics (FPMD) simulations under identical conditions [53].
    • Against Experimental Data: If available, compare results with experimental data inferred from spectroscopic studies or kinetic models. Acknowledge that direct experimental measurement of diffusion in supercritical fluids at high P-T conditions is challenging.
Protocol 2: Benchmarking Hydrogen Diffusion in Metals with Defects

This protocol is based on a study investigating H diffusion in ruthenium with grain boundaries, highlighting the importance of defects [21].

  • 1. System Setup with Defects:

    • Structure Generation: Create atomic structures that include the defects of interest.
      • Pristine Crystal: Create a perfect Ru crystal lattice as a control.
      • Grain Boundaries (GBs): Use crystallographic tools to construct specific GBs (e.g., Σ7 tilt and Σ7 twist GBs) within the simulation cell [21].
    • Hydrogen Insertion: Randomly insert H atoms into interstitial sites (e.g., octahedral/tetrahedral) of the metal lattice.

  • 2. Force Field Parameterization and Training:

    • Training Set: Compile a training set from ab initio (DFT) calculations, including:
      • Equations of state for different metal crystal structures.
      • Surface energies.
      • Adsorption energies of the diffusant (H) on surfaces.
      • Hydride formation energies.
      • Bond length scans and cluster calculations [21].
    • Optimization: Use a global optimization algorithm (e.g., Monte Carlo) to fit ReaxFF parameters to the ab initio training set, minimizing an objective function that weighs the differences between ReaxFF and reference values [21].

  • 3. Molecular Dynamics Simulation for Diffusion:

    • Simulation Settings: Perform MD simulations in the NVT ensemble across a range of temperatures (e.g., 600–1500 K). Use a small time step (e.g., 0.25 fs) due to the light mass of hydrogen and the high fidelity required for bond-order updates.
    • Trajectory Output: Save atomic positions frequently (e.g., every 1000 steps) for subsequent analysis.

  • 4. Analysis of Diffusion Pathways and Coefficients:

    • MSD and D: Calculate the MSD of H atoms and derive the diffusion coefficient as in Protocol 1.
    • Pathway Analysis: Visualize simulation trajectories to qualitatively observe H atom trapping at GBs and preferred diffusion pathways (along or across GB planes).
    • Arrhenius Analysis: Fit the temperature-dependent diffusion coefficients to the Arrhenius equation, ( D = D0 \exp(-Ea / kB T) ), to extract the activation energy (( Ea )) and pre-exponential factor (( D_0 )).

  • 5. Validation:

    • Against DFT: Compare the ReaxFF-predicted H solution energies, diffusion barriers in the pristine lattice, and GB structures with the original DFT data.
    • Against Experiment: Compare the calculated diffusion coefficients and activation energies with experimental measurements, if available.

Table 4: Key Computational Tools for ReaxFF Benchmarking

Tool Name Type / Category Primary Function in Benchmarking Example Use Case
ReaxFF Force Field [2] Reactive Potential Provides the core interatomic potential for MD simulations, enabling bond breaking/forming. Simulating chemical reactions in geofluids or SEI formation.
DFT/VASP [21] Ab Initio Electronic Structure Generates high-quality reference data for the force field training set and validation. Calculating adsorption energies, reaction barriers, and equations of state.
LAMMPS/PuReMD [2] Molecular Dynamics Engine Performs the actual ReaxFF MD simulations, calculating forces and integrating equations of motion. Running the NVT/NpT production simulations for diffusion.
MDAnalysis [55] [21] Trajectory Analysis Analyzes MD trajectories to compute properties like MSD, RDF, and coordination numbers. Calculating the diffusion coefficient from the saved trajectory file.
ASE (Atomic Simulation Environment) [55] Python Library A versatile framework for setting up, running, visualizing, and analyzing atomistic simulations. Managing simulation workflows and interfacing between different codes.
PyMatgen [55] Python Library Assists in materials analysis, handling structural manipulations, and accessing crystallographic databases. Generating and analyzing grain boundary structures in metals.
AiiDA [55] Workflow Management Platform Manages, automates, and tracks complex simulation workflows, ensuring reproducibility. Orchestrating the entire parameterization-validation loop.

Workflow Visualization of a ReaxFF Simulation for Diffusion

The following diagram details the specific workflow for running a ReaxFF simulation to compute a diffusion coefficient, from initial configuration to final result.

G Config Initial System Configuration Equil Equilibration (NpT) Stabilize P, T, Density Config->Equil ReaxFF ReaxFF Force Field ReaxFF->Equil Prod Production Run (NVT) Save Trajectory ReaxFF->Prod Equil->Prod Analysis Trajectory Analysis Calculate MSD Prod->Analysis Result Diffusion Coefficient (D) via Einstein Relation Analysis->Result

Comparative Analysis of Different ReaxFF Parameter Sets

The Reactive Force Field (ReaxFF) is a powerful computational tool designed to bridge the gap between highly accurate but computationally expensive quantum mechanical (QM) methods and efficient but non-reactive classical force fields [2]. By employing a bond-order formalism, ReaxFF can simulate chemical reactions, including bond breaking and formation, without the need for predefined connectivity, making it uniquely suited for studying complex reactive processes in materials science, catalysis, and battery research [2]. The interatomic potential in ReaxFF calculates the total system energy as a sum of various contributions, including bond energy (E_bond), angle strain (E_angle), torsion energy (E_tors), and non-bonded interactions (van der Waals and Coulombic) [2]. A key feature is its use of a continuous bond-order function calculated from interatomic distances, which allows for a smooth and differentiable potential energy surface necessary for molecular dynamics (MD) simulations [2].

The accuracy and transferability of a ReaxFF simulation are critically dependent on the parameter set used. These parameters, which can number in the hundreds, are typically optimized against a training set of QM data to describe the potential energy surface for a specific set of elements and chemical environments [2] [56]. Presently, there are two major, intra-transferable branches of ReaxFF parameterizations: the combustion branch, which focuses on accurately describing gas-phase species like O2 and H2O, and the aqueous branch, which is targeted at condensed-phase aqueous chemistry [12]. Selecting an appropriate parameter set from the correct branch is therefore a foundational step for any reliable ReaxFF study. This application note provides a comparative analysis of available parameter sets and detailed protocols for their application, with a specific focus on calculating diffusion coefficients—a key property in energy storage materials research.

Comparative Analysis of ReaxFF Parameter Sets

The performance of a ReaxFF simulation is intrinsically linked to the chosen parameter set. Researchers must select a parameterization that is not only trained for the correct elements but is also part of a consistent branch (aqueous or combustion) to ensure internal transferability. The table below summarizes key available force fields and their characteristics.

Table 1: Overview of Selected ReaxFF Parameter Sets

Force Field Name Elements Covered Training Focus & Application Examples ReaxFF Branch
CHO.ff [12] C, H, O Hydrocarbon oxidation; combustion dynamics [12]. Combustion
HCONSB.ff [12] H, C, O, N, S, B Coal char combustion; soot formation; extends CHO.ff [12]. Combustion
HE.ff [12] C, H, O, N High explosives (e.g., RDX); thermal decomposition [12]. Combustion
CuCl-Hâ‚‚O.ff [12] Cu, Cl, H, O Aqueous chloride and copper chloride chemistry [12]. Aqueous
FeOCHCl.ff [12] Fe, O, C, H, Cl Iron-oxyhydroxide systems; corrosion; mineralogy [12]. Aqueous
AuCSOH.ff [12] Au, C, S, O, H Gold surfaces and nanoparticles; cold welding of oxidized surfaces [12]. Aqueous
AB.ff [12] H, O, N, B Ammonia borane dehydrogenation and combustion [12]. Combustion

It is strongly advised against mixing parameters from different branches or sets without rigorous reparameterization and validation. Using a force field for systems outside its training set can produce unrealistic results [12]. For instance, a force field like CHO.ff is excellent for gas-phase combustion but would be inappropriate for simulating aqueous transition metal ions. Furthermore, later parameterizations often extend and improve upon earlier ones; the 2008-C/H/O description fully contains and extends the 2001 hydrocarbon description, and the 2010/2011 Si/O/H parameterizations were validated against the full 2003-Si/O/H training set [2].

Parameter Set Selection and Reparameterization Challenges

When an existing parameter set is insufficient, a common approach is to refit a subset of parameters relevant to the new system of interest. This reparameterization is typically done by minimizing the difference between ReaxFF results and reference QM data, often using energies or atomic forces. Force-matching, which aims to replicate QM-derived atomic force vectors, is an alternative to the more common energy-based fitting [56]. This procedure is complex, as the objective function must compare vectors across multiple atoms and configurations. Research has evaluated several metrics for this purpose, including Euclidean distance, cosine similarity, and Spearman's footrule, with findings indicating that the footrule method can yield superior parameters for certain systems like transition metal oxides [56].

Recent work on lithium-ion battery (LIB) materials highlights both the necessity and difficulty of reparameterization. Available ReaxFF force fields for LIBs successfully reproduced dissociation energies but failed to accurately describe the solid-phase properties of key inorganic salts like Lithium Fluoride (LiF) [8]. A dedicated reparameterization of Li-F interactions was required to correct for unrealistic lithium diffusivity in the solid lattice, improving its prediction by two orders of magnitude [8]. This underscores a critical point: the training set dictates the force field's capabilities. A set trained only on dissociation energies will not automatically extrapolate to correctly model crystal properties or mass transport. Consequently, ReaxFF is best employed for well-defined phenomena, and its application to new properties often necessitates an interactive reparameterization protocol to build a representative training dataset [8].

Experimental Protocols for Diffusion Coefficient Calculations

Calculating diffusion coefficients using ReaxFF Molecular Dynamics (MD) is a common method for studying mass transport in materials, such as lithium ions in battery electrodes. The following section outlines a standardized workflow and a detailed protocol based on a study of a lithiated sulfur cathode [4].

The process, from system preparation to data analysis, can be visualized in the following workflow diagram.

G Start Start: System Setup A Import Crystal Structure (CIF file) Start->A B Insert Li Ions (Builder/GCMC) A->B C Geometry Optimization + Lattice Relaxation B->C D Simulated Annealing (Amorphization) C->D E Equilibration MD D->E F Production MD E->F G Trajectory Analysis F->G H Calculate MSD G->H I Calculate VACF G->I J Fit D from MSD slope H->J K Integrate D from VACF I->K End Final Diffusion Coefficient (D) J->End K->End

Detailed Step-by-Step Protocol

This protocol details the calculation of lithium ion diffusion coefficients in a Li0.4S cathode material [4].

Part 1: System Generation and Equilibration

  • Import Structure and Insert Ions:

    • In the AMSinput graphical interface, import the crystalline sulfur (Sα) structure from a CIF file.
    • Use the Edit → Builder menu to insert lithium atoms. Enter the SMILES code [Li] and specify the number of molecules (e.g., 51 Li atoms for Li0.4S). Click Generate Molecules to randomly place the ions within the simulation box [4].
    • Alternative Method: For a more thermodynamically representative structure, use Grand Canonical Monte Carlo (GCMC) insertion instead of the builder.

  • Geometry Optimization with Lattice Relaxation:

    • Set the Task to Geometry Optimization.
    • Select the appropriate force field file (e.g., LiS.ff).
    • In the Details → Geometry Optimization panel, tick the Optimize lattice checkbox.
    • Run the calculation and update the AMSinput structure upon completion. The unit cell volume should increase significantly after relaxation [4].

  • Create Amorphous System via Simulated Annealing:

    • Change the Task to Molecular Dynamics.
    • Set the number of steps to 30,000 (or more for better statistics).
    • Configure the temperature profile for annealing using a Berendsen thermostat:
      • Step 1: 300 K for 5,000 steps (equilibration).
      • Step 2: Ramp from 300 K to 1600 K over 20,000 steps (heating).
      • Step 3: Ramp from 1600 K to 300 K over 5,000 steps (rapid cooling).
    • Run the MD simulation and subsequently perform a final geometry optimization (with lattice relaxation) on the resulting amorphous structure [4].

Part 2: Production MD and Data Analysis

  • Set Up Production MD Run:

    • Set the Task to Molecular Dynamics.
    • In the MD details, set the total number of steps (e.g., 110,000: 10,000 equilibration + 100,000 production).
    • Set the Sample frequency to 5 (writes trajectory every 5 steps). With a typical time step of 0.25 fs, this yields a trajectory with coordinates saved every 1.25 fs [4].
    • Set the thermostat to a constant temperature (e.g., 1600 K for high diffusivity).

  • Calculate Diffusion Coefficient via Mean Squared Displacement (MSD - Recommended):

    • After the calculation, open the trajectory in AMSmovie.
    • Navigate to MD Properties → MSD.
    • Set the Atoms to Li to analyze only lithium ions.
    • Adjust the Steps and Max MSD Frame to select a stable, linear region of the MSD plot.
    • The diffusion coefficient ( D ) is calculated from the slope of the MSD versus time plot using the equation: [ D = \frac{\text{slope}(MSD)}{6} ] where the slope is obtained from a linear fit. The resulting ( D ) value will be displayed [4].

  • Calculate Diffusion Coefficient via Velocity Autocorrelation Function (VACF):

    • In AMSmovie, select MD Properties → Autocorrelation function.
    • Set Property to Diffusion Coefficient (D) and Atoms to Li.
    • The diffusion coefficient is computed by integrating the VACF over time: [ D = \frac{1}{3} \int{0}^{t{\text{max}}} \langle \mathbf{v}(0) \cdot \mathbf{v}(t) \rangle dt ] The value of ( D ) is read from the plateau of the integral curve at long times [4].

  • Extrapolation to Lower Temperatures:

    • To estimate ( D ) at room temperature, run production MD simulations at multiple elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K).
    • Create an Arrhenius plot of ( \ln(D(T)) ) versus ( 1/T ).
    • Perform a linear fit to determine the activation energy ( Ea ) and pre-exponential factor ( D0 ) from the equation: [ \ln D(T) = \ln D0 - \frac{Ea}{k_B} \cdot \frac{1}{T} ]
    • Use these parameters to extrapolate the diffusion coefficient to 300 K [4].

This section lists key software tools and computational "reagents" essential for conducting ReaxFF simulations and analyses.

Table 2: Essential Computational Tools for ReaxFF Research

Tool / Resource Type Primary Function in ReaxFF Research
LAMMPS [2] Software Package A highly popular open-source MD code that integrates the ReaxFF potential, enabling large-scale parallel simulations.
AMS/ReaxFF [4] Software Package A commercial software suite (SCM) with a user-friendly GUI (AMSinput) for setting up and analyzing ReaxFF simulations, including tutorials for properties like diffusion.
PuReMD [2] Software Package The Purdue Reactive Molecular Dynamics code, optimized for efficient ReaxFF simulations.
GULP [56] Software Package A code for performing energy calculations and force-fitting, often used in the parameter optimization loop.
ASE [8] Python Library The Atomic Simulation Environment; used for scripting, manipulating atoms, and interfacing with various MD/DFT codes, facilitating workflow automation.
PyMatgen [8] Python Library The Python Materials Genomics library; useful for structure analysis and generating input files for materials simulations.
Force Field File (.ff) [57] Data File A text file following a specific format that contains all parameters (general, atomic, bonds, angles, etc.) defining the ReaxFF potential for a set of elements.
Training Set Data Set A curated collection of QM reference data (energies, forces, charges) used to parameterize and validate a ReaxFF force field.

The ReaxFF reactive force field is an indispensable tool for simulating reactive processes across a wide range of scientific fields. Its utility, however, is governed by the careful selection and application of appropriate parameter sets. Researchers must be cognizant of the distinctions between the aqueous and combustion branches and the limitations of existing parameterizations. As demonstrated in battery and transition metal oxide research, moving beyond the capabilities of an existing force field requires a meticulous and often system-specific reparameterization process. The protocols outlined herein, from force field selection and modification to the calculation of key properties like diffusion coefficients, provide a framework for conducting robust and reliable ReaxFF molecular dynamics simulations. Future developments will likely focus on creating more versatile parameter sets and integrating machine learning approaches to enhance the accuracy and transferability of this powerful simulation method.

In the field of computational materials science, particularly in the study of lithium-ion batteries using molecular dynamics, the accuracy of force fields is paramount. Claims of improvement, especially those as substantial as "two orders of magnitude," represent significant breakthroughs in methodology. This application note examines concrete examples of such improvements within the context of ReaxFF molecular dynamics simulations, with a specific focus on the calculation of diffusion coefficients. We detail the experimental protocols that validate these advancements and provide the framework for researchers to assess such claims in their own work. The ability to accurately quantify and verify substantial improvements in predictive accuracy is fundamental to advancing battery material design and simulation reliability.

A Case Study in ReaxFF Reparameterization

Context and Improvement

A seminal example of a two-order-of-magnitude improvement comes from a recent reparameterization of the ReaxFF force field for simulating components of the solid-electrolyte interphase (SEI) in lithium-ion batteries. The study specifically targeted the inorganic salt Lithium Fluoride (LiF), a critical SEI component known for its beneficial passivation properties [8].

The key achievement was that the optimized ReaxFF surpassed the previously available force field by accurately adjusting the diffusivity of lithium in the solid lattice, resulting in a two-order-of-magnitude improvement in its prediction at room temperature [8]. This enhancement addressed a critical flaw in earlier force fields, which failed to correctly describe the solid nature of LiF and its mass transport properties.

Quantitative Significance

An order of magnitude represents a ten-fold (10x) difference on a logarithmic scale [58]. Consequently, a two-order-of-magnitude improvement corresponds to a 100-fold (100x) increase in accuracy in the prediction of the lithium diffusivity. In practical terms, this means that the newly parameterized force field produces diffusion coefficients that are one hundred times closer to the expected experimental or ab initio values than the previous model. This is not a minor adjustment but a qualitative leap in the force field's predictive capability for a crucial material property.

Table 1: Interpretation of Order-of-Magnitude Improvements

Improvement Claim Numerical Factor Impact on Predictive Accuracy
One Order of Magnitude 10x Substantial improvement, often a minimum for a paradigm shift
Two Orders of Magnitude 100x Radical improvement, correcting a fundamental model failure
Three Orders of Magnitude 1000x Transformative improvement, enabling entirely new capabilities

Experimental Protocols for Validating Diffusion Coefficient Improvements

The validation of a claimed improvement in diffusion coefficients requires rigorous methodology. The following protocols, standard in ReaxFF molecular dynamics tutorials and research, outline the process for calculating diffusion coefficients and, by extension, verifying enhancements [4].

Protocol 1: Diffusion Coefficient via Mean Squared Displacement (MSD)

The Mean Squared Displacement method is the recommended approach for calculating diffusion coefficients from MD trajectories [4].

Detailed Methodology:

  • Production MD Simulation: Run a sufficiently long molecular dynamics simulation under the desired thermodynamic conditions (e.g., NVT ensemble at a specific temperature).
  • Trajectory Sampling: Save the atomic positions (trajectory) at a regular frequency (e.g., every 5 steps). The time between saved frames is Δt = sample_frequency × time_step [4].
  • MSD Calculation: For the species of interest (e.g., Li atoms), calculate the MSD from the trajectory. The MSD is defined as: MSD(t) = ⟨[r(0) - r(t)]²⟩ where r(t) is the position at time t, and the angle brackets denote an average over all atoms and time origins [4].
  • Linear Regression: The diffusion coefficient D is obtained from the slope of the linear region of the MSD versus time plot using the Einstein relation: D = slope(MSD) / (6) (The divisor is 6 for 3-dimensional diffusion).
  • Convergence Check: Ensure the MSD plot is a straight line. A non-linear MSD indicates insufficient simulation time or that the system has not reached a diffusive regime. The calculated D should be stable over different time segments of the trajectory [4].

Protocol 2: Diffusion Coefficient via Velocity Autocorrelation Function (VACF)

The Velocity Autocorrelation Function provides an alternative method, though it requires higher-frequency sampling of velocities [4].

Detailed Methodology:

  • Production MD Simulation with Velocity Output: Run an MD simulation as in Protocol 1, but ensure that atomic velocities are saved at a high frequency (a small sample_frequency).
  • VACF Calculation: Calculate the velocity autocorrelation function for the atoms: VACF(t) = ⟨v(0) · v(t)⟩
  • Integration: The diffusion coefficient is obtained by integrating the VACF over time: D = (1/3) ∫ VACF(t) dt The integral is evaluated from t=0 to t=t_max [4].
  • Validation: The result should be compared with the MSD method. The value of D from the VACF integral should converge to a horizontal line for large enough times [4].

Protocol 3: Extrapolation to Lower Temperatures via Arrhenius Behavior

Direct MD simulation at low temperatures (e.g., room temperature) can be prohibitively long due to slow dynamics. The Arrhenius equation allows for extrapolation from higher-temperature simulations [4].

Detailed Methodology:

  • Multi-Temperature Simulations: Perform production MD simulations (using Protocol 1 or 2) at a minimum of four different elevated temperatures (e.g., 600 K, 800 K, 1200 K, 1600 K) [4].
  • Calculate D(T): Obtain the diffusion coefficient D at each temperature T.
  • Arrhenius Plot: Plot the natural logarithm of the diffusion coefficient, ln D(T), against the inverse temperature, 1/T.
  • Linear Fit and Extraction of Parameters: Fit the data points to the Arrhenius equation: ln D(T) = ln Dâ‚€ - (Eₐ / k_B) * (1/T) The slope of the linear fit is -Eₐ / k_B, from which the activation energy Eₐ can be calculated. The y-intercept is ln Dâ‚€, the pre-exponential factor [4].
  • Extrapolation: Use the fitted parameters to calculate D at lower, experimentally relevant temperatures.

Table 2: Key Experimental Protocols for Diffusion Coefficient Analysis

Protocol Name Core Equation Key Requirement Primary Application
Mean Squared Displacement (MSD) D = slope(MSD)/6 Long trajectory for linear MSD Recommended method for most cases [4]
Velocity Autocorrelation (VACF) D = (1/3) ∫ VACF(t) dt High-frequency velocity sampling Alternative method; good for validation
Arrhenius Extrapolation D(T) = D₀ exp(-Eₐ / k_B T) Simulations at multiple temperatures Estimating low-T diffusivity from high-T MD

Workflow Visualization

The following diagram illustrates the logical workflow for assessing a two-order-of-magnitude improvement, integrating the protocols described above.

G Start Start: Force Field Reparameterization MD1 Run MD Simulations with Original Force Field Start->MD1 Protocol 1, 2, or 3 MD2 Run MD Simulations with Enhanced Force Field Start->MD2 Protocol 1, 2, or 3 Calc1 Calculate Diffusion Coefficient (D_old) MD1->Calc1 Calc2 Calculate Diffusion Coefficient (D_new) MD2->Calc2 Compare Compare D_new vs. D_old Calc1->Compare Calc2->Compare Result Verify Two-Order-of-Magnitude Improvement (100x) Compare->Result

Diagram 1: Workflow for assessing a two-order-of-magnitude improvement in diffusion coefficients.

The Scientist's Toolkit: Essential Research Reagents and Materials

The following table details key computational "reagents" and resources essential for conducting the experiments described in this application note.

Table 3: Research Reagent Solutions for ReaxFF MD Studies

Item Name Function / Purpose Example / Specification
ReaxFF Force Field Defines interatomic potentials for reactive MD simulations. LiS.ff; Parameter sets for C-H-O-Li-Si-Li-F [4] [8]
MD Simulation Engine Software to perform the molecular dynamics calculations. AMS with ReaxFF engine [4]
Structure Visualization & Analysis Visualize trajectories, monitor simulations, and calculate properties. AMSmovie, AMSinput [4]
Python Libraries (ASE, PyMatgen) Automate simulation workflows, manage atomistic systems, and analyze data. Used for robust automation of reparameterization steps [8]
Reference Diffusion Data Experimental or ab initio values for benchmark comparisons. e.g., Li+ in water: 1.030 × 10⁻⁹ m²/s (from PhreeqC database) [59]
Initial Structure Files Define the atomic starting configuration of the system. CIF files for crystals; pre-relaxed .xyz files [4]

The reactive force-field (ReaxFF) method has established itself as a powerful computational tool for exploring, developing, and optimizing material properties by enabling the simulation of chemical reactions at scales inaccessible to quantum mechanical (QM) methods [2]. By employing a bond-order formalism, ReaxFF implicitly describes chemical bonding without expensive QM calculations, thus allowing simulations to consider the full dynamic evolution of a system involving bond formation and breakage [2]. However, traditional ReaxFF, like other classical force fields, does not explicitly treat electrons as independent entities, limiting its direct application to redox processes where electron transfer is fundamental.

The novel eReaxFF method addresses this limitation by extending the standard ReaxFF framework to allow for the simulation of explicit electrons treated in a pseudoclassical manner [38] [60]. This approach is orders of magnitude faster than quantum chemical methods while retaining ReaxFF's transferability [38]. eReaxFF integrates the Atom condensed Kohn-Sham DFT approximated to second order (ACKS2) charge calculation scheme, enabling the force field to capture electron affinities of various species with good qualitative agreement to experimental data [60]. This advancement opens new avenues for studying large-scale chemical and physical systems involving electron transfer, such as those found in electrochemical energy storage, corrosion, and catalytic processes.

This application note details the protocols for employing eReaxFF to simulate electron transfer dynamics, using a hydrocarbon radical system as a foundational case study. The content is framed within broader thesis research on ReaxFF molecular dynamics, particularly focusing on methodologies for calculating diffusion coefficients, thereby providing researchers with a practical guide for implementing this technique in their investigations of redox-active systems.

Theoretical Foundation and System Setup

Fundamental Concepts of eReaxFF

The eReaxFF method is a pseudoclassical treatment of explicit electrons within the ReaxFF framework. Its fundamental innovation lies in representing electrons as independent, explicit particles that can be added to a molecular system. These electrons possess a negative charge and are treated similarly to other atomic species within the simulation, albeit with their own specific parameterization [60]. The force field is trained to capture electron affinities, ensuring that the behavior of these explicit electrons qualitatively matches expectations from experimental data and more computationally intensive Ehrenfest dynamics simulations [60].

A key aspect of the methodology is the integration of the ACKS2 (Atom condensed Kohn-Sham DFT approximated to second order) charge calculation scheme, which enables a more accurate description of charge distribution and polarization effects in the presence of explicit electrons [60]. Notably, standard ReaxFF parameters are largely transferable to the eReaxFF method, facilitating the application of existing parameter sets to new systems involving explicit electrons [60].

Model System: A Hydrocarbon Radical Anion

The prototypical system for demonstrating eReaxFF capabilities consists of a hydrocarbon radical, C₁₂H₁₉• [38]. This molecule is engineered to contain both a conjugated (polyacetylene-like) segment and an aliphatic segment, with a radical site located on the terminal aliphatic carbon (labeled CH₂).

  • Ground State: The system's ground state is a primary carbanion, where the explicit electron is localized at the radical site on the aliphatic chain.
  • Excited State Anion: The simulation begins with an "excited" anion state generated by inserting an explicit electron (El) into the conjugated part of the radical, approximately 5 pm away from a specific carbon atom (#3). From this non-equilibrium starting point, the electron diffuses through the molecular chain until it eventually localizes at the radical site, reaching the ground state [38].

This electron transfer process can be quantitatively monitored by observing the total energy of the system, which exhibits a noticeable drop once the electron settles at its stable, ground-state position [38].

Research Reagent Solutions

The table below catalogues the essential computational components and their functions required to set up and run an eReaxFF simulation.

Table 1: Key Research Reagents and Computational Materials

Item Name Function / Description Critical Specifications / Notes
Hydrocarbon Radical (C₁₂H₁₉•) Model system for studying electron transfer; consists of conjugated and aliphatic parts with a terminal radical site [38]. The radical site acts as the electron trap. The conjugated segment facilitates electron delocalization during transfer.
Explicit Electron Particle (El) A pseudoclassical particle representing an electron, added to the system to form the anion [38]. Treated as a distinct particle type with a charge of -1. Requires a specific charge constraint to maintain its identity.
ReaxFF Force Field Provides the interatomic potential describing reactive interactions. The CHONSMgPNaFBLi-e.ff parameter set is used [38]. The -e suffix indicates compatibility with the explicit electron model. Parameters are trained against QM data including electron affinities [60].
Charge Constraint A computational restraint applied to the region containing the electron particle to maintain its charge at -1 throughout the simulation [38]. Essential to prevent the charge equilibration scheme from distributing the electron's charge across the entire system.

Computational Protocol

This section provides a detailed, step-by-step methodology for simulating electron transfer in the hydrocarbon radical system using eReaxFF, as implemented in the AMS software suite.

Initial System Configuration

  • Import Structure: Begin by importing the initial geometry of the C₁₂H₁₉• radical (C12H19.xyz) into AMSinput via File → Import Coordinates [38].
  • Add Explicit Electron:
    • In the Element tool, select the electron (El) from the periodic table [38].
    • Initially, place the electron particle near the radical structure in the graphical viewer.
  • Define Electron Region:
    • Navigate to Model → Regions [38].
    • Select the electron particle and click Add to create a new region (e.g., named 'El'). This region will be used to apply a charge constraint.
  • Apply Charge Constraint:
    • Go to Model → Charge constraints [38].
    • Click Add, select the 'El' region, and set its Charge to -1. This ensures the electron particle retains its full negative charge.
  • Position the Electron:
    • Select the electron particle, then hold Shift and select carbon atom #3.
    • Using the distance slider or entry field, set the distance between them to 5 pm. This places the electron in its initial excited state position within the conjugated chain [38].

Simulation Parameters

  • Main Settings:
    • Set the Task to Molecular Dynamics.
    • Set the Total charge to -1 to account for the added electron.
    • In the ReaxFF panel, select the CHONSMgPNaFBLi-e.ff force field file [38].
  • Molecular Dynamics Details:
    • Set the Number of steps to 750,000.
    • Set the Time step to 0.1 fs.
    • Set the Sample frequency to 500 (writes trajectory data every 50 fs) [38].
  • Thermostat Configuration:
    • Select the Berendsen thermostat.
    • Set the Temperature to 600 K. Elevated temperatures can accelerate the electron transfer process for observation within feasible simulation times.
    • Set the Damping constant to 100 fs [38].
  • Execution: Save the input file and run the calculation. A warning about atoms being too close may appear due to the initial proximity of the electron and carbon atom #3 and can be ignored [38].

Workflow Visualization

The following diagram illustrates the logical workflow for setting up and running an eReaxFF simulation, from system preparation to analysis.

Start Start: System Setup A Import Hydrocarbon Radical (C₁₂H₁₉•) Geometry Start->A B Add Explicit Electron (El) from Periodic Table A->B C Define 'El' Region and Apply Charge Constraint (-1) B->C D Position Electron 5 pm from Carbon #3 C->D E Configure ReaxFF/MD Parameters: Forcefield, Thermostat, Steps D->E F Run Molecular Dynamics Simulation E->F G Analyze Results: Trajectory & Energy F->G End Interpret Electron Transfer Dynamics G->End

Diagram 1: eReaxFF simulation setup and execution workflow.

Analysis and Interpretation

Qualitative Trajectory Analysis

The simulation progress and outcome can be initially assessed by visually inspecting the trajectory in AMSmovie [38].

  • Open Trajectory: Upon completion, open the calculation in AMSmovie and start the playback.
  • Observe Electron Dynamics: You will observe the explicit electron diffusing through the hydrocarbon radical. The electron typically moves more freely through the conjugated segment, while the junction between the conjugated and aliphatic parts may act as a temporary stability trap [38].
  • Identify Ground State Formation: The key event is the electron's transfer to the terminal aliphatic radical site. This is often marked by a significant drop in the total energy of the system, indicating the formation of the more stable ground state carbanion [38]. The simulation's inherent randomness means transfer times will vary between runs; one example reported a transfer time of approximately 13.75 ps [38].

Quantitative Data Extraction

For a more rigorous analysis, two primary quantitative methods can be employed:

  • Electron Transfer Time: The time taken for the electron to transfer from its initial position to the radical site can be extracted directly from the trajectory by identifying the frame where the energy drop occurs [38].
  • Time-Averaged Electron Position: The average position of the electron along the molecular backbone can be computed using scripting tools like the PLAMS Python library available in the AMS package. This provides a statistical measure of electron localization and dynamics [38].

Table 2: Key Quantitative Outcomes from a Representative eReaxFF Simulation

Metric Observation / Value Significance
Electron Transfer Time ~13.75 ps (example, varies by run) [38] Indicates the timescale for electron migration through the molecular chain to the stable site.
Energy Change upon Localization Observable drop in total energy [38] Confirms the system has reached a lower energy ground state (primary carbanion).
Electron Diffusion Path Preferential diffusion through conjugated chain; trapping at chain intersection [38] Reveals the influence of molecular structure on electron transfer barriers and pathway.

The eReaxFF methodology represents a significant step forward in reactive molecular dynamics, bridging the gap between classical force fields and quantum mechanical accuracy for processes involving explicit electron transfer. By treating electrons as pseudoclassical particles, it enables the study of redox processes, electron transport in molecular systems, and radiation damage in materials at scales and timeframes that were previously prohibitive.

The protocol outlined herein for a hydrocarbon radical system serves as a foundational tutorial that can be adapted and extended to more complex, technologically relevant redox systems. Future applications of eReaxFF are vast and could include:

  • Battery Materials: Modeling the reduction and oxidation processes at electrode-electrolyte interfaces in Li-ion and Li-S batteries, complementing existing ReaxFF studies on Li-ion diffusion [4] [19].
  • Corrosion Science: Providing atomic-scale insights into the initial stages of metal and alloy oxidation, building upon ReaxFF MD studies of oxidation behavior in materials like Ni-Al alloys [61].
  • Biomolecular Redox Chemistry: Simulating electron transfer chains in proteins or the redox chemistry of drug molecules.
  • Radiation Chemistry: Investigating the behavior of solvated electrons and subsequent radical reactions in materials exposed to radiation.

As force field parameterizations continue to improve and computational resources grow, eReaxFF is poised to become an indispensable tool for exploring the dynamic role of electrons in complex chemical and material systems.

Conclusion

This tutorial demonstrates that ReaxFF molecular dynamics provides a powerful framework for calculating diffusion coefficients in complex reactive systems, successfully bridging the gap between quantum mechanical accuracy and computational feasibility for large-scale simulations. The methodologies outlined—from fundamental system preparation to advanced validation techniques—enable researchers to reliably model mass transport phenomena in applications ranging from battery materials to biomedical systems. Key takeaways include the critical importance of addressing finite-size effects, the value of multi-method validation through both MSD and VACF analysis, and the potential of temperature extrapolation techniques to access experimentally relevant conditions. Future directions should focus on enhanced parameterization protocols for specific material classes, integration with machine learning approaches for accelerated sampling, and application of emerging methods like eReaxFF for systems requiring explicit electron treatment. As ReaxFF continues to evolve, its capacity to illuminate diffusion-driven processes will prove increasingly valuable for designing next-generation energy storage materials and understanding molecular transport in biological environments.

References