Benchmarking Force Fields for Accurate Transport Properties: A Comprehensive Guide for Biomedical Research

Abstract

Accurately predicting transport properties like diffusion, viscosity, and conductivity is critical for biomedical applications, from drug delivery to electrolyte design. However, the choice of force field significantly impacts the reliability of molecular dynamics simulations. This article provides a comprehensive framework for benchmarking classical and machine-learned force fields. We explore foundational concepts, methodological applications for complex fluids and polymers, strategies to overcome common pathologies, and rigorous validation protocols. By synthesizing the latest advances, this guide empowers researchers to select, optimize, and validate force fields for trustworthy predictions of dynamic properties in biological and materials systems.

The Critical Role of Force Fields in Predicting Transport Properties

Why Transport Properties Are Pivotal for Biomedical and Materials Applications

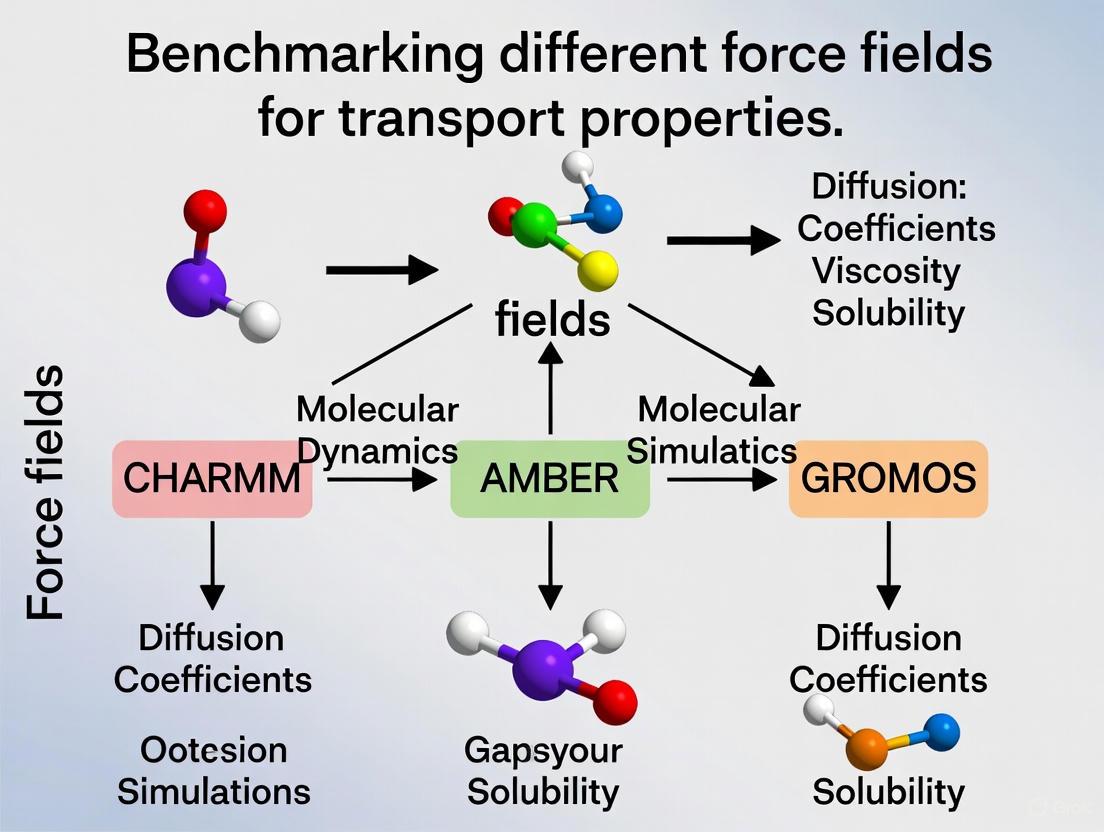
Transport properties—such as viscosity, diffusivity, and electrical conductivity—are critical performance metrics in molecular dynamics (MD) simulations. For researchers in biomedicine and materials science, accurately predicting these properties is essential for designing effective drugs, catalysts, and functional materials. This guide benchmarks the performance of different molecular force fields in predicting key transport properties, providing a foundation for selecting the right model for your research.

Force Fields and Transport Properties

Molecular dynamics simulations rely on force fields—empirical mathematical models that calculate the potential energy of a system of atoms. The accuracy of these simulations in predicting real-world behavior depends entirely on the quality of the force field used. While many force fields accurately predict structural properties, correctly capturing dynamic transport properties presents a greater challenge [1] [2].

The Critical Role of Transport Properties

• Drug Design: Molecular diffusivity and membrane permeability influence drug absorption and distribution.
• Biomolecular Function: Ion conductivity and transport rates are crucial for understanding ion channel proteins and nucleic acid behavior [3].
• Materials Performance: Viscosity and electrical conductivity determine the efficiency of lubricants, batteries, and catalysts [1] [2].
• Process Optimization: Accurate transport properties enable reliable simulation of industrial processes like steelmaking and glass manufacturing [2].

Comparative Performance of Force Fields

The table below summarizes the performance of various force fields across different applications and transport properties:

Table 1: Force Field Performance Across Applications

Application Domain	Force Fields Compared	Key Transport Properties	Performance Summary
β-Peptides & Biomolecules	CHARMM, Amber, GROMOS [4]	Structural stability, oligomer formation	CHARMM reproduced experimental structures accurately in all monomeric simulations and correctly described all oligomeric examples [4].
Lubricants & Long-Chain Molecules	L-OPLS-AA (all-atom) vs. united-atom [1]	Shear viscosity, diffusion	All-atom L-OPLS-AA accurately predicted viscosity; united-atom models significantly under-predicted viscosity (by ~50% for C16 molecules) [1].
Oxide Melts & Materials	Matsui, Guillot, Bouhadja [2]	Self-diffusion coefficients, electrical conductivity	Bouhadja's force field showed best agreement with experimental activation energies and robust transferability [2].
Liquid Membranes	GAFF, OPLS-AA/CM1A, CHARMM36, COMPASS [5]	Shear viscosity, diffusion, interfacial tension	CHARMM36 and COMPASS provided accurate density and viscosity; GAFF and OPLS-AA overestimated viscosity by 60-130% [5].
Machine Learning Force Fields	CHGNet, M3GNet, MACE, MatterSim, SevenNet, Orb [6]	Structural stability, mechanical properties	Orb and MatterSim demonstrated strongest robustness (100% simulation completion), while CHGNet and M3GNet suffered >85% failure rates [6].

Specialized Performance Insights

Table 2: Detailed Force Field Performance Metrics

Force Field	System Type	Key Strengths	Documented Limitations
CHARMM	β-peptides [4], liquid membranes [5]	Accurate structural reproduction, good viscosity prediction	Requires specific extensions for non-natural peptidomimetics [4].
L-OPLS-AA (all-atom)	Lubricants (n-hexadecane) [1]	Excellent viscosity prediction, accurate friction behavior	Higher computational cost than united-atom models [1].
Bouhadja BMH Potential	Oxide melts (CaO-Al₂O₃-SiO₂) [2]	Best dynamic property prediction, good transferability	Less accurate for certain structural features compared to Matsui [2].
Machine Learning (Orb, MatterSim)	Universal materials [6]	Broad chemical coverage, good simulation stability	Systematic density errors >2%, performance correlates with training data representation [6].

Experimental Protocols and Methodologies

Viscosity Calculation Protocol

For lubricant simulations [1]:

• System Setup: Construct a box of 130 n-hexadecane molecules with periodic boundary conditions
• Simulation Parameters: Use velocity-Verlet integration with 1.0 fs timestep, constrain fast-moving bonds with SHAKE algorithm
• Equilibrium Phase: Conduct equilibrium MD (EMD) simulations at target temperatures and pressures
• Viscosity Calculation: Apply Green-Kubo formula to stress tensor autocorrelation functions: η = (V/kBT) ∫₀∞ ⟨Pαβ(t) · Pαβ(0)⟩dt where V is volume, T is temperature, and Pαβ are off-diagonal elements of the pressure tensor

Ion Transport Validation

For Mg²⁺ ion models in biological systems [3]:

• System Preparation: Simulate single Mg²⁺ ion in ~1000 water molecules using AMBER14
• Validation Metrics:
  • Radial distribution functions (RDF) compared to experimental Mg²⁺-O distances
  • Solvation free energy calculation using thermodynamic integration
  • Water exchange rate from coordinated shell using transition state theory
  • Diffusion constants from mean-squared displacement calculations
• Force Field Forms: Compare standard 12-6 Lennard-Jones potentials versus 12-6-4 potentials with charge-induced dipole term

Membrane System Characterization

For liquid membrane simulations [5]:

• Property Calculations:
  • Density: NPT ensemble simulations at 243-333K
  • Shear Viscosity: Equilibrium MD with Green-Kubo method
  • Interfacial Tension: Liquid-liquid interface simulations using mechanical pressure tensor
  • Partition Coefficients: Free energy calculations for ethanol in DIPE+Ethanol+Water systems
• Validation: Compare all calculated properties against experimental measurements

Decision Framework for Force Field Selection

The diagram below illustrates the systematic process for selecting an appropriate force field based on your research system and target properties:

Table 3: Key Computational Tools and Resources for Transport Property Studies

Tool/Resource	Function	Application Examples
GROMACS [4]	High-performance MD simulation engine	Impartial force field comparison using same algorithms [4]
LAMMPS [1]	Molecular dynamics simulator	Lubricant and materials simulations [1]
AMBER [3]	Biomolecular simulation package	Mg²⁺ ion validation studies [3]
Green-Kubo Method [1]	Calculate transport properties from EMD	Viscosity calculation for n-hexadecane [1]
Mean-Squared Displacement (MSD) [7]	Determine diffusion coefficients	Particle mobility in various systems [7]
UniFFBench [6]	ML force field benchmarking framework	Evaluate UMLFFs against experimental data [6]

No single force field excels universally across all systems and transport properties. Classical force fields like CHARMM and all-atom L-OPLS-AA provide reliable performance for specific biomolecular and liquid systems, while specialized potentials like Bouhadja's BMH potential offer advantages for oxide melts. Emerging machine learning force fields show promise for universal application but require careful validation against experimental transport properties.

For research prioritizing transport properties, validation against experimental viscosity, diffusion, or conductivity data is essential—excellent performance on structural benchmarks does not guarantee accurate dynamic property prediction [1] [6]. The force field selection must balance computational efficiency with the specific accuracy requirements of your biomedical or materials application.

Molecular dynamics (MD) simulations serve as a cornerstone of atomistic-scale analysis across numerous disciplines, including materials science, drug development, and biochemistry [8]. These computational methods allow researchers to observe the time-dependent behavior of atomic and molecular systems, providing insights that are often difficult or impossible to obtain experimentally. The central dilemma in MD simulations revolves around the choice between computational accuracy and system size/timescale. On one end of the spectrum, ab initio molecular dynamics (AIMD) provides high accuracy by computing electronic structure from first principles, while classical molecular dynamics (CMD) sacrifices quantum mechanical precision to access dramatically larger systems and longer timescales [2]. This fundamental trade-off between scale and accuracy forms the critical decision point for researchers selecting computational approaches for specific scientific questions. The emergence of machine-learning molecular dynamics (MLMD) has further complicated this landscape, offering a potential middle ground with near-ab initio accuracy and improved computational efficiency [8]. Understanding the precise capabilities, limitations, and appropriate applications of each method is essential for advancing computational research across scientific domains.

Theoretical Foundations and Force Fields

The divergence between classical and ab initio MD approaches originates in their fundamentally different treatment of atomic interactions. Ab initio MD relies on quantum mechanical calculations, typically using density functional theory (DFT), to compute interatomic forces by explicitly solving for electronic structure at each simulation step [9]. This parameter-free approach naturally captures complex quantum effects, including chemical bond formation and breaking, charge transfer, and electronic polarization. In contrast, classical MD employs empirically parameterized force fields—mathematical functions that approximate the potential energy surface of a system using pre-defined terms for bond stretching, angle bending, torsional rotations, and non-bonded interactions [1]. These force fields are typically optimized to reproduce either experimental data or results from higher-level quantum calculations for specific classes of compounds [10].

The computational frameworks for these methods reflect their different theoretical foundations. CMD simulations predominantly utilize highly optimized packages like LAMMPS that can efficiently evaluate simple analytical functions across millions of atoms [1] [10]. AIMD implementations, such as those in CP2K or Quantum ESPRESSO, focus instead on solving the electronic structure problem with sufficient accuracy while managing the substantially greater computational load [2]. The recently developed MLMD approaches, including DeePMD-kit and Allegro, represent a hybrid strategy—using neural networks trained on quantum mechanical data to create force fields that retain much of the accuracy of AIMD while approaching the computational efficiency of CMD [8] [11].

Experimental Benchmarking Methodologies

Robust benchmarking is essential for validating both classical force fields and ab initio methods. The protocols differ according to the intended application domain and the fundamental limitations of each approach.

For classical force field validation, the typical workflow involves:

• System Preparation: Constructing initial atomic configurations using tools like Packmol, with careful attention to representative system sizes that minimize finite-size effects while remaining computationally tractable [10].
• Equilibration: Performing extended sampling under appropriate thermodynamic ensembles (NPT for density equilibration, NVT for production runs) while monitoring convergence through energy and density fluctuations [10].
• Property Calculation: Computing structural properties (radial distribution functions, coordination numbers), thermodynamic properties (density, heat capacity), and transport properties (viscosity, diffusion coefficients) from production trajectories [2] [1].
• Experimental Comparison: Validating simulation results against experimental measurements across a range of conditions to assess transferability beyond parameterization domains [10].

For ab initio and MLMD validation, the focus shifts toward accuracy assessment:

• Quantum Mechanical Reference: Generating high-quality reference data using well-converged DFT calculations or higher-level quantum chemical methods [12].
• Property Accuracy: Comparing energy, force, and property predictions against quantum mechanical benchmarks, with particular attention to subtle effects like van der Waals interactions and transition states [8].
• Performance Metrics: Evaluating computational efficiency through time-to-solution metrics (e.g., nanoseconds per day) and parallel scaling characteristics on high-performance computing architectures [11].

Figure 1: MD Method Selection Workflow. This decision tree illustrates the key factors driving the choice between molecular dynamics approaches, highlighting the central trade-off between accuracy and scale.

Performance Comparison: Accuracy, Scale, and Computational Efficiency

Quantitative Performance Metrics

The practical implications of the methodological differences between classical, ab initio, and machine-learning MD approaches become evident when examining specific performance metrics across multiple dimensions. The tables below summarize key comparative data for these methods.

Table 1: Time and Power Consumption Comparison of MD Methods

Method	Time Consumption (ηt, second/step/atom)	Power Consumption (ηp, Watt)	Typical System Size	Typical Time Scale
Ab Initio MD (AIMD)	10-3–100	106–107 (CPU/GPU) [8]	100-1,000 atoms [2]	Picoseconds [11]
Machine-Learning MD (MLMD)	10-6–10-3	104–105 (CPU/GPU) [8]	105–107 atoms [11]	Nanoseconds [11]
Classical MD (CMD)	10-9–10-6	103–104 (CPU/GPU) [8]	106–109 atoms [2]	Nanoseconds to microseconds [1]
Special-Purpose MDPU	~10-9 (vs. AIMD) [8]	~103–104 [8]	Not specified	Not specified

Table 2: Accuracy Comparison Across MD Methods for Various Systems

System	Method	Energy Error (εe, meV/atom)	Force Error (εf, meV/Å)	Experimental Agreement
Au	MLMD (MDPU)	85.35	173.20	Accurate under shock compression [8]
Cu	MLMD (MDPU)	1.84	16.44	Accurate strain-stress curve [8]
Hâ‚‚O	MLMD (MDPU)	7.62	148.24	Accurate radial distribution function [8]
CaO-Al₂O₃-SiO₂	CMD (Bouhadja FF)	Not specified	Not specified	Good for dynamics, fair for structure [2]
CaO-Al₂O₃-SiO₂	CMD (Matsui FF)	Not specified	Not specified	Good for structure, poor for dynamics [2]
n-hexadecane	CMD (L-OPLS-AA)	Not specified	Not specified	Accurate density/viscosity [1]
PDMS	CMD (Huang FF)	Not specified	Not specified	Good thermodynamic properties [10]

Table 3: Recent Performance Advances in Neural Network MD (as of 2024)

Software	System	# Atoms	Hardware	Performance (ns/day)
DeePMD-kit (optimized)	Cu	0.5M	576K cores, Fugaku	149 [11]
DeePMD-kit (optimized)	Hâ‚‚O	0.5M	576K cores, Fugaku	68.5 [11]
DeePMD-kit (baseline)	Cu	2.1M	218.8K cores, Fugaku	4.7 [11]
Allegro	Ag	1M	128 A100 GPUs	49.4 [11]
SNAP ML-IAP	C	1B	27.3K GPUs, Summit	1.03 [11]

The performance data reveals several critical patterns. First, the computational efficiency gap between methods spans multiple orders of magnitude, with classical MD exceeding ab initio MD in speed by approximately 10³-10⁹ times depending on the specific implementation and hardware [8]. This efficiency comes at the cost of parameterization dependence—classical force fields must be carefully selected and validated for specific systems and conditions, as their accuracy varies significantly across different chemical environments [2] [1]. The emergence of specialized hardware like the MD Processing Unit (MDPU) promises to further reshape this landscape, potentially reducing time and power consumption by approximately 10³ times compared to state-of-the-art MLMD based on CPU/GPU [8].

Force Field Accuracy and Transferability

The accuracy of classical MD simulations is intrinsically linked to the quality and transferability of the employed force fields. Recent benchmarking studies reveal substantial variations in performance across different force fields and material systems. For CaO-Al₂O₃-SiO₂ melts, Bouhadja's force field demonstrates superior performance in capturing melt dynamics and conductivity trends, while Matsui's force field provides more accurate structural predictions [2]. Similarly, for organic systems, all-atom force fields like L-OPLS-AA significantly outperform united-atom variants in predicting viscosity and structural properties of long-chain molecules like n-hexadecane [1].

The transferability of force fields beyond their parameterization domain remains a persistent challenge. In polysiloxane systems, force fields specifically parameterized for PDMS (e.g., Huang's model) generally outperform general-purpose force fields like OPLS-AA and Dreiding in predicting thermodynamic and transport properties [10]. This underscores the importance of domain-specific parameterization and the limitations of transferable force fields for applications requiring quantitative accuracy.

Application Guidelines: Selecting the Appropriate Method

Problem-Method Alignment

Choosing the appropriate MD method requires careful consideration of the specific scientific question, accuracy requirements, and available computational resources. The following guidelines emerge from the performance benchmarking:

Ab Initio MD is recommended for:

• Studying chemical reactions with bond formation/breaking [8]
• Investigating electronic properties and charge transfer phenomena [9]
• Systems where no reliable classical force fields exist [12]
• Generating reference data for force field parameterization [10]

Classical MD is preferred for:

• Large-scale systems (>100,000 atoms) requiring statistical sampling [2]
• Processes requiring microsecond timescales or longer [1]
• Calculating transport properties like viscosity and diffusion [10]
• Systems with well-parameterized, validated force fields [1]

Machine-Learning MD is optimal for:

• Applications requiring near-ab initio accuracy at larger scales [11]
• Systems where AIMD is too costly but CMD is insufficiently accurate [8]
• Complex processes involving both structural dynamics and electronic effects [11]

The Scientist's Toolkit: Essential Research Solutions

Table 4: Essential Software and Computational Tools for Molecular Dynamics Research

Tool Name	Type	Primary Function	Applicable Methods
LAMMPS	Software Package	High-performance MD simulation with extensive force field support [1] [10]	CMD, MLMD
DeePMD-kit	Software Package	Neural network MD with ab initio accuracy [11]	MLMD
CP2K	Software Package	Ab initio MD using DFT [8]	AIMD
Quantum ESPRESSO	Software Package	Open-source suite for ab initio calculations [8]	AIMD
Packmol	Tool	Initial configuration generation for MD simulations [10]	All methods
COMPASS	Force Field	Class II force field for various materials including siloxanes [10]	CMD
OPLS-AA	Force Field	All-atom force field for organic liquids [1] [10]	CMD
MDPU	Hardware	Special-purpose processor for MD simulations [8]	All methods
L-Alanine isopropyl ester	L-Alanine isopropyl ester, MF:C6H13NO2, MW:131.17 g/mol	Chemical Reagent	Bench Chemicals
Antibacterial agent 199	Antibacterial agent 199, MF:C37H48N6O8, MW:704.8 g/mol	Chemical Reagent	Bench Chemicals

The evolving landscape of molecular dynamics simulations continues to offer researchers an expanding array of computational tools, each with characteristic strengths and limitations. The fundamental trade-off between spatial/temporal scale and quantum mechanical accuracy remains, but the boundaries are continually being pushed forward through methodological innovations. Machine-learning approaches are particularly promising, already demonstrating the ability to simulate systems of millions of atoms with ab initio accuracy at unprecedented timescales—reaching 149 nanoseconds per day for copper systems on advanced supercomputing architectures [11]. Special-purpose hardware like the MDPU suggests a pathway to further dramatic efficiency improvements, potentially reducing time and power consumption by orders of magnitude compared to current CPU/GPU-based approaches [8].

For researchers, the critical imperative remains the careful matching of method to scientific question, with explicit consideration of accuracy requirements, system size, timescale needs, and available computational resources. As force field development continues to advance—with more sophisticated parameterization approaches and better understanding of transferability limitations—classical MD will maintain its essential role for large-scale and long-timescale simulations. Simultaneously, the ongoing integration of machine learning with traditional quantum mechanical approaches promises to further blur the lines between accuracy and efficiency, potentially making ab initio quality simulations accessible for increasingly complex systems and phenomena relevant to drug development, materials design, and fundamental scientific discovery.

The accurate prediction of transport properties—diffusion, viscosity, and ionic conductivity—is fundamental to advancements in materials science, drug development, and energy storage technologies. These dynamic properties govern processes ranging from ion transport through biological membranes to the flow behavior of industrial melts and electrolytes. Molecular dynamics (MD) simulations have emerged as a powerful tool for investigating these properties at the atomistic level, but their predictive accuracy depends entirely on the underlying empirical force fields that describe interatomic interactions. Force fields are mathematical representations of the potential energy surface that determine how atoms interact, making them the foundational component of any classical MD simulation. The challenge researchers face is that numerous force fields exist, each with different parameterization strategies, functional forms, and applicability domains, leading to significant variations in their predictive performance for transport properties.

This guide provides a comprehensive benchmarking analysis of popular force fields across diverse chemical systems, presenting quantitative performance data and detailed methodological protocols. As force field selection critically influences simulation outcomes, systematic comparison enables researchers to make informed choices specific to their systems of interest. Recent studies have demonstrated that force field transferability—the ability to perform accurately outside original parameterization ranges—remains a significant challenge, particularly for dynamic properties that require longer simulation timescales. Furthermore, the emergence of machine learning force fields promises to bridge the accuracy gap between classical MD and quantum-mechanical methods while maintaining computational feasibility for larger systems. By objectively comparing force field performance across multiple chemical domains and providing standardized assessment methodologies, this guide serves as an essential resource for researchers requiring reliable transport property predictions.

Performance Comparison of Force Fields Across Systems

The accuracy of force fields varies significantly across different chemical systems and target properties. The tables below summarize quantitative performance data from recent benchmarking studies.

Oxide Melts (CaO-Al₂O₃-SiO₂ System)

Table 1: Force field performance for structural and transport properties of oxide melts [2] [13]

Force Field	Density Prediction	Si–O Coordination	Al–O Coordination	Self-Diffusion Coefficients	Electrical Conductivity	Transferability Assessment
Matsui	Accurate across compositions	Excellent agreement with AIMD	Less accurate vs. AIMD	Moderate accuracy	Underestimates experimental values	Limited beyond original parameterization
Guillot	Accurate across compositions	Excellent agreement with AIMD	Less accurate vs. AIMD	Moderate accuracy	Underestimates experimental values	Limited beyond original parameterization
Bouhadja	Slightly less accurate	Good agreement with AIMD	Best agreement with AIMD	Best agreement with experiments	Best agreement with experiments	Excellent transferability

Organic Liquids and Membranes

Table 2: Force field performance for diisopropyl ether (DIPE) and related systems [5]

Force Field	Density Deviation	Viscosity Deviation	Interfacial Tension	Mutual Solubility	Partition Coefficients	Recommended Application
GAFF	+3% to +5%	+60% to +130%	Not assessed	Not assessed	Not assessed	Not recommended for transport properties
OPLS-AA/CM1A	+3% to +5%	+60% to +130%	Not assessed	Not assessed	Not assessed	Not recommended for transport properties
COMPASS	<±1%	<±15%	Good agreement with experiments	Reasonable prediction	Good agreement with experiments	Acceptable for membrane systems
CHARMM36	<±1%	<±15%	Best agreement with experiments	Best prediction	Best agreement with experiments	Recommended for liquid membranes

Biological Nanopores

Table 3: Force field comparison for ionic and electroosmotic flows in biological nanopores [14]

Force Field	Cation-Anion Selectivity	Electroosmotic Flow Direction	Flow Magnitude	Ion Conductivity	Viscosity	Consistency Across Systems
CHARMM36 (+TIP3P)	Coherent across force fields	Coherent across force fields	Quantitative differences	Varies significantly	Varies significantly	Good for wider pores
Amber-ff14SB (+TIP3P)	Coherent across force fields	Coherent across force fields	Quantitative differences	Varies significantly	Varies significantly	Good for wider pores
Amber-ff19SB (+OPC)	Coherent across force fields	Coherent across force fields	Quantitative differences	Varies significantly	Varies significantly	Significant differences in narrow pores

Experimental Protocols for Force Field Benchmarking

Standardized Workflow for Transport Property Calculation

Property-Specific Methodologies

Diffusion Coefficient Calculations

Self-diffusion coefficients are typically calculated using the Einstein relation from mean squared displacement (MSD) data [2]. The standard protocol involves:

• Production MD: Run extended NVT simulations (typically 1-10 ns depending on system size and temperature) after thorough equilibration.
• Trajectory Analysis: Calculate MSD for each atom type using MSD = ⟨|r(t) - r(0)|²⟩ where r(t) is the position at time t.
• Linear Regression: Fit the MSD curve in the diffusive regime (typically after initial ballistic motion) using MSD = 6Dt + C, where D is the self-diffusion coefficient.
• Averaging: Average results over multiple time origins and all atoms of the same type to improve statistics.

For ionic systems, both cation and anion diffusion coefficients should be calculated separately, as their relationship determines overall conductivity [15].

Viscosity Calculations

Shear viscosity is most accurately calculated using the Green-Kubo formalism, which relates viscosity to the integral of the stress autocorrelation function [5]:

• Stress Tensor Collection: During production MD, save the full pressure tensor (including off-diagonal components) at high frequency (every 1-10 fs).
• Autocorrelation Calculation: Compute the autocorrelation function of the pressure tensor elements: C(t) = ⟨P_ab(t)P_ab(0)⟩ where a and b denote Cartesian components.
• Integration: Calculate viscosity from η = (V/kBT) ∫ C(t) dt where V is volume, kB is Boltzmann's constant, and T is temperature.
• Averaging: Average results over all independent off-diagonal components (xy, xz, yz) and multiple time origins.

For complex systems, running multiple independent replicas is recommended to obtain reliable error estimates.

Ionic Conductivity Calculations

Ionic conductivity can be computed via two primary approaches [2] [15]:

A. Einstein-Based Approach:

• Calculate the mean squared displacement of the collective ion displacement vector.
• Apply the relationship σ = (e²/6VkBT) * d/dt ⟨[∑ z_i (r_i(t) - r_i(0))]²⟩ where zi is the ion charge and ri is its position.
• This approach naturally includes the effect of ion-ion correlations.

B. Green-Kubo Approach:

• Calculate the current autocorrelation function: C(t) = ⟨J(t) · J(0)⟩ where J(t) = ∑ z_i v_i(t) is the total current.
• Integrate to obtain conductivity: σ = (1/3VkBT) ∫ C(t) dt.
• This method is particularly sensitive to statistical quality and requires long simulation times.

The Nernst-Einstein approximation, which neglects ion correlations, often overestimates conductivity and should be used with caution, particularly in confined systems [15].

Emerging Methods: Neural Network Force Fields

Traditional force fields show limitations in transferability and accuracy, particularly for complex charged fluids and systems with significant electronic polarization effects. Neural network force fields (NNFF) have emerged as promising alternatives that combine near-quantum accuracy with classical MD efficiency [16] [15].

NNFF Performance Advantages

Recent studies demonstrate that NNFFs successfully address pathological deficiencies in classical force field simulations:

• Improved Dynamic Properties: NeuralIL, a neural network potential for ionic liquids, correctly predicts transport properties where classical non-polarizable force fields fail, accurately capturing hydrogen bonding dynamics and proton transfer reactions [16].
• Accurate Confined System Modeling: For aqueous NaCl in graphene slit pores, NNFFs reveal that ionic conductivity decreases under nanoconfinement, a trend governed by changes in both ion self-diffusion and dynamic ion-ion correlations [15].
• Electronic Effects: NNFFs naturally capture polarization and charge transfer effects without explicit parameterization, overcoming a fundamental limitation of fixed-charge force fields [16].

Implementation Workflow for NNFFs

Table 4: Key computational tools for force field benchmarking studies

Resource Category	Specific Tools	Primary Function	Application Notes
MD Simulation Engines	LAMMPS, GROMACS, NAMD	Molecular dynamics trajectory generation	LAMMPS preferred for materials science; GROMACS for biomolecules [17] [18]
Force Field Libraries	CHARMM, AMBER, OPLS, GAFF, COMPASS	Parameter sets for different molecule classes	CHARMM36 shows good performance for organic membranes [5]
Quantum Chemistry Codes	VASP, Quantum ESPRESSO, ABACUS	Reference calculations for training NNFFs	Essential for generating training data [17]
Workflow Management	APEX, Dflow, Pyiron	Automated property calculation workflows	APEX enables high-throughput screening [17]
Analysis Tools	Pymatgen, VASPKIT, PLUMED	Trajectory analysis and enhanced sampling	Critical for extracting transport properties [17] [18]
Visualization Software	VMD, OVITO, MayaVi	Molecular structure and property visualization	Important for qualitative assessment and figure generation

This comparison guide demonstrates that force field selection profoundly impacts the accuracy of transport property predictions in molecular dynamics simulations. For oxide melt systems, Bouhadja's force field outperforms alternatives for dynamic properties, while in organic membrane systems, CHARMM36 and COMPASS provide superior performance for ether-based liquids. In biological nanopores, significant variations exist between force fields, particularly under tight confinement.

The emergence of machine learning force fields represents a paradigm shift, offering quantum-chemical accuracy while maintaining computational feasibility for large systems. As these methods continue to mature, they promise to resolve longstanding challenges in simulating complex charged fluids and confined systems. However, traditional empirical force fields remain valuable for many applications, particularly when selected based on comprehensive benchmarking studies like those presented here.

Future directions in the field include the development of standardized benchmarking protocols, increased integration of automated workflow platforms like APEX, and continued refinement of neural network potentials through active learning approaches. By carefully selecting force fields based on their validated performance for specific systems and properties, researchers can significantly enhance the reliability of their molecular simulations for predicting diffusion, viscosity, and ionic conductivity.

Molecular dynamics (MD) simulations serve as a cornerstone tool for investigating the structural and transport properties of complex molecular systems across chemistry, materials science, and biology. The predictive accuracy of these simulations is critically dependent on the quality of the empirical force fields that describe interatomic interactions. This guide provides a systematic comparison of force field performance for three distinct classes of materials—polymers, ionic liquids, and biological nanopores—focusing specifically on their ability to reproduce experimental transport properties. Accurate modeling of these properties is essential for applications ranging from industrial polymer processing and electrochemical device design to single-molecule sensing.

Force Field Benchmarking for Polymers

Polydimethylsiloxane (PDMS) as a Model System

Polydimethylsiloxane (PDMS) is a widely used silicon-based polymer recognized for its unique thermal stability, viscoelasticity, and biocompatibility. Its properties present a rigorous test for force field parameterization, requiring accurate modeling of flexible siloxane backbones and diverse intermolecular interactions.

Table 1: Comparison of Force Fields for Polydimethylsiloxane (PDMS)

Force Field	Type	Key Features / Parametrization Basis	Performance on Thermodynamic Properties (Density, Heat Capacity)	Performance on Transport Properties (Viscosity, Thermal Conductivity)
OPLS-AA	All-Atom (AA)	Class I; universal force field for organic liquids; partial charges recalculated for PDMS [10].	Moderate accuracy [10].	Significant discrepancies common [10].
Dreiding	All-Atom (AA)	Class I; universal force field; includes H-bond interactions [10].	Moderate accuracy [10].	Significant discrepancies common [10].
COMPASS	All-Atom (AA)	Class II; universal force field; includes specific parametrization for siloxane environments [10].	Good agreement with experimental density and heat capacity [10].	Varies; generally more reliable than Class I FFs [10].
Huang's Model	All-Atom (AA)	Class II; specifically parametrized for PDMS using bottom-up (QM) and top-down (experimental) data [10].	Excellent agreement with experimental data [10].	Superior performance in predicting viscosity and thermal conductivity [10].
Frischknecht (UA)	United-Atom (UA)	Hybrid Class I/II; specifically parametrized for PDMS; faster computation [10].	Good agreement with structural and pressure properties [10].	Good performance reported [10].

Experimental Protocols for Polymer Force Field Validation

The benchmarking of PDMS force fields involves well-defined computational and experimental procedures to assess a wide range of properties [10].

• System Preparation: Initial configurations are created by randomly placing multiple PDMS polymer chains (e.g., 20 chains of 30 monomers each) in a simulation box using tools like Packmol to mimic the liquid state.
• Equilibration Protocol: The system is first energy-minimized. It is then equilibrated in the isothermal-isobaric (NPT) ensemble at the target temperature (e.g., 300 K) and pressure (1 atm) until the density and total energy converge to stable values. This ensures the system has reached a realistic equilibrium state.
• Production Simulation: Following equilibration, a production run is performed in the canonical (NVT) or microcanonical (NVE) ensemble to generate trajectory data for property calculation.
• Property Calculation:
  • Density: Directly measured from the average simulation box volume during the NPT ensemble.
  • Self-Diffusion Coefficient: Calculated from the mean-squared displacement of polymer chains using the Einstein relation.
  • Viscosity: Computed using the Green-Kubo relation, which integrates the autocorrelation function of the off-diagonal elements of the pressure tensor, or via non-equilibrium MD methods.
  • Thermal Conductivity: Determined using the Green-Kubo approach by integrating the heat current autocorrelation function.

Figure 1: Workflow for benchmarking polymer force fields through molecular dynamics simulations.

Force Field Benchmarking for Ionic Liquids

All-Atom and Coarse-Grained Challenges

Ionic liquids (ILs) are salts in the liquid state at room temperature, characterized by complex nanostructures arising from Coulombic, hydrogen-bonding, and van der Waals interactions. Their high viscosity and compositional diversity make force field development challenging [19] [20].

Table 2: Comparison of All-Atom Force Fields for Ionic Liquids ([C4mim][BF4])

Force Field	Type	Density (kg/m³) at 298 K	Cation Diffusion (10⁻¹¹ m²/s) at 343 K	Key Features / Notes
OPLS-based	All-Atom	1178 [19]	7.3 [19]	Original version; often requires charge scaling for accurate dynamics [19].
0.8*OPLS	All-Atom	1150 [19]	43.1 [19]	Refined OPLS with 0.8 charge scaling factor; improves dynamics [19].
SAPT-based	All-Atom	1180 [19]	1.1 [19]	Parametrized from Symmetry-Adapted Perturbation Theory calculations [19].
CL&P	All-Atom	1154 [19]	1.19 [19]	Specifically developed for ILs [19].
AMOEBA-IL	Polarizable All-Atom	1229 (at 313 K) [19]	2.9 [19]	Includes polarization effects via induced atomic dipoles [19].
APPLE&P	All-Atom	1193 [19]	1.01 [19]	Known for good accuracy across various ILs and properties [19].
Experimental Data	---	~1170 [19]	~40.0 [19]	Reference values for validation [19].

Advanced Modeling Techniques for Ionic Liquids

Given the computational cost of AA models for large systems, coarse-grained (CG) models are often employed. Furthermore, incorporating polarization is critical for an accurate description of IL properties [19].

• Coarse-Grained (CG) Models: CG models, such as those based on the MARTINI framework, group multiple atoms into a single interaction site. This dramatically increases computational efficiency and allows access to larger spatial and temporal scales. Parameterization can follow a "top-down" approach (fitting to macroscopic experimental data) or a "bottom-up" approach (matching statistics from AA simulations, e.g., using Inverse Boltzmann Inversion or force-matching) [19].
• Polarizable Models: The polar nature of ILs means that the electronic environment of an ion is significantly influenced by its neighbors. Polarizable force fields account for this by using methods like the Drude oscillator model or induced dipoles, which lead to more accurate predictions of dynamic properties like diffusion and conductivity compared to fixed-charge models [19].
• Machine Learning Potentials: Emerging as a powerful tool, ML potentials can approach quantum-level accuracy while retaining computational efficiency comparable to classical force fields. They can be trained on data from Density Functional Theory (DFT) calculations and experimental observables to correct known inaccuracies of the underlying quantum method [21].

Force Field Benchmarking for Biological Nanopores

Proteins in Hybrid Ordered-Disordered Systems

Biological nanopores are protein channels that facilitate transport across cell membranes. They are prime targets for MD simulation due to their application in single-molecule sensing, including DNA sequencing and protein analysis. Accurate simulation of these systems is challenging as they often contain both well-structured domains and intrinsically disordered regions (IDRs) with highly diverse dynamics [22] [23].

• Structured vs. Disordered Regions: Traditional force fields like Amber99SB-ILDN and CHARMM22/27 were primarily optimized for folded, globular proteins. When applied to IDRs, they often produce overly compact structures that do not match experimental data from techniques like NMR and SAXS, a problem linked partly to the water model used (e.g., TIP3P) [22] [24].
• Improved Force Fields and Water Models: Modern force fields such as CHARMM36m and combinations like Amber99SB-ILDN with the TIP4P-D water model have shown significant improvement. The TIP4P-D water model, in particular, was found to prevent artificial structural collapse in IDRs and yield more realistic NMR relaxation properties [22].
• Validation with NMR Relaxation: NMR relaxation parameters (R₁, Râ‚‚, and NOE) are highly sensitive to ps-ns timescale dynamics and are therefore a critical benchmark for force field performance on hybrid proteins. Accurate prediction of these parameters is a stringent test of a force field's ability to capture the dynamics of both ordered and disordered regions [22].

Table 3: Performance of Force Fields for Proteins with Structured and Disordered Regions

Force Field & Water Model Combination	Performance on Structured Domains	Performance on Disordered Regions	Ability to Retain Transient Helical Motifs	Overall Recommendation
A99/TIP3P	Good [22]	Poor (artificial collapse) [22]	Variable [22]	Not recommended for IDPs/hybrids [22].
A99/TIP4P-D	Good [22]	Good (improved expansion) [22]	Improved [22]	Recommended [22].
C22*/TIP3P	Good [22]	Poor to Moderate [22]	Variable [22]	Not recommended [22].
C22*/TIP4P-D	Good [22]	Good [22]	Good [22]	Recommended [22].
C36m/TIP3P	Good [22]	Moderate [22]	Best [22]	Good, but water model matters [22].
C36m/TIP4P-D	Good [22]	Good [22]	Best [22]	Highly Recommended [22].

Experimental Protocols for Nanopore Force Field Validation

Benchmarking force fields for biological nanopores and hybrid proteins relies heavily on comparing simulation outputs with high-resolution experimental data [22].

• System Setup: The protein of interest is solvated in a water box (e.g., a rhombic dodecahedron) with a minimum distance between the protein and box edge (e.g., 2 nm). The system is neutralized with counterions, and salt concentration is adjusted to match experimental conditions (e.g., 100 mM NaCl). Periodic boundary conditions are applied.
• Simulation Parameters: Simulations are typically performed using a 2 fs time step with bonds involving hydrogen atoms constrained. Long-range electrostatics are treated with particle mesh Ewald (PME). Temperature and pressure are controlled using coupling algorithms (e.g., Nosé-Hoover, Parrinello-Rahman).
• Equilibration and Production: The system undergoes step-wise energy minimization and equilibration first with positional restraints on protein heavy atoms (to relax solvent and ions), and then without restraints. A production simulation of microsecond duration is typically required to adequately sample the conformations of disordered regions.
• Validation against Experimental Data:
  • Small-Angle X-ray Scattering (SAXS): The theoretical scattering profile is calculated from the MD trajectory and compared to experimental data, with the radius of gyration (Rg) being a key parameter.
  • NMR Spectroscopy: A multitude of NMR observables can be predicted and compared:
    • Chemical Shifts: Calculated directly from trajectory structures using empirical predictors like SHIFTX/SPARTA+.
    • Residual Dipolar Couplings (RDCs): Calculated from the average orientation of bond vectors relative to a global alignment tensor.
    • Paramagnetic Relaxation Enhancement (PRE): Calculated from the distance between a paramagnetic label and nuclear spins.
    • Relaxation Rates (R₁, Râ‚‚) and NOE: Calculated from the autocorrelation function of bond vector fluctuations (e.g., N-H vector), providing insight into picosecond-to-nanosecond dynamics.

The Scientist's Toolkit: Essential Research Reagents and Materials

Table 4: Key Reagents and Computational Tools for Force Field Benchmarking

Reagent / Tool	Function / Purpose	Example Systems / Notes
CHARMM36m	All-atom force field for proteins.	Particularly good for proteins with disordered regions and membrane proteins like nanopores [22].
Amber99SB-ILDN	All-atom force field for proteins.	Often used as a base; performance improved with better water models [22].
TIP4P-D	Water model.	Corrects for deficiencies in TIP3P; reduces collapse in intrinsically disordered proteins [22].
Huang's PDMS FF	All-atom, class II force field for polymers.	Specifically parametrized for polydimethylsiloxane; shows superior performance [10].
APPLE&P	Force field for ionic liquids.	Known for its general accuracy and reliability across various IL properties [19].
LAMMPS	Molecular dynamics simulation package.	Widely used for polymers, inorganic systems, and coarse-grained models [10].
GROMACS	Molecular dynamics simulation package.	Very common in the academic community for biomolecular simulations [22].
Packmol	Software for building initial configurations.	Used to pack polymer chains or molecules into simulation boxes [10].
18-carboxy dinor Leukotriene B4	18-carboxy dinor Leukotriene B4 | Research Biomarker	18-carboxy dinor Leukotriene B4: A key LTB4 metabolite biomarker for inflammation & immunology research. For Research Use Only. Not for human use.
1-Palmitoyl-d9-2-hydroxy-sn-glycero-3-PE	1-Palmitoyl-d9-2-hydroxy-sn-glycero-3-PE|Lysophospholipid	1-Palmitoyl-d9-2-hydroxy-sn-glycero-3-PE, a deuterated lysophosphatidylethanolamine internal standard. For Research Use Only. Not for human or veterinary use.

Figure 2: The iterative cycle of force field validation, where simulation predictions are constantly compared against experimental benchmarks.

The benchmarking studies reviewed in this guide consistently demonstrate that the choice of force field is profoundly system-dependent and critically influences the accuracy of predicted transport and structural properties. Key findings indicate that system-specific force fields (e.g., Huang's for PDMS, APPLE&P for ILs) generally outperform universal models. For complex biological systems like hybrid proteins with disordered regions, the combination of a modern force field (CHARMM36m) with an appropriate water model (TIP4P-D) is essential. Furthermore, incorporating polarization effects for ionic liquids and using advanced machine-learning potentials trained on both quantum mechanical and experimental data represent the forefront of achieving higher accuracy across all classes of materials. As the field progresses, systematic validation against a broad set of experimental data remains the gold standard for evaluating and developing trustworthy force fields for molecular simulations.

In computational chemistry and materials science, force fields are fundamental for molecular dynamics (MD) simulations, enabling the prediction of properties and behaviors at the atomic scale. However, the selection of a force field is not a neutral decision; it is a critical parameter that can fundamentally alter the outcome of a simulation. This guide provides a systematic, objective comparison of various force fields, benchmarking their performance primarily on transport properties—such as diffusion and viscosity—which are highly sensitive to the underlying potential energy surface. Supported by quantitative data and detailed experimental protocols, this analysis aims to equip researchers with the evidence needed to select the most appropriate model for their specific systems, particularly in materials science and drug development contexts.

Force Field Performance at a Glance

The table below summarizes the performance of several prominent force fields across different material systems and key properties, highlighting the specific nature of their discrepancies.

Force Field	Material System	Key Performance Findings	Magnitude of Discrepancy	Ref
GAFF	Diisopropyl Ether (DIPE) Liquid Membrane	Overestimated density and shear viscosity.	Density: +3-5%Viscosity: +60-130%	[5]
OPLS-AA/CM1A	Diisopropyl Ether (DIPE) Liquid Membrane	Overestimated density and shear viscosity.	Density: +3-5%Viscosity: +60-130%	[5]
CHARMM36	Diisopropyl Ether (DIPE) Liquid Membrane	Accurate density and viscosity; recommended for ether-based membranes.	Accurate density & viscosity	[5]
COMPASS	Diisopropyl Ether (DIPE) Liquid Membrane	Quite accurate density and viscosity.	Accurate density & viscosity	[5]
ff99SB	Alanine Peptides (Ala3, Ala5) in Water	Excellent agreement with NMR data; performance depends on water model.	Accurate NMR observables	[25]
MACE Scratch	Cr-doped Sb₂Te₃ (2D Material)	Catastrophic failure predicting migration barrier; poor extrapolation.	Overestimated barrier by >4 eV	[26]
MACE Foundation	Cr-doped Sb₂Te₃ (2D Material)	Qualitatively plausible but quantitatively inaccurate barrier.	Overestimated barrier by ~0.7 eV	[26]
MACE Fine-Tuned	Cr-doped Sb₂Te₃ (2D Material)	Dramatically improved barrier prediction after specialization.	Accurate barrier prediction	[26]

Quantitative Discrepancies in Key Properties

Density and Shear Viscosity

For liquid membranes, thermodynamic and transport properties are critical. A comparison of four all-atom force fields for modeling diisopropyl ether (DIPE) revealed significant differences in predicting density and shear viscosity [5].

• GAFF & OPLS-AA/CM1A: Both overestimated the density of DIPE across a temperature range of 243–333 K by 3-5% and, more dramatically, the shear viscosity by 60-130% [5].
• CHARMM36 & COMPASS: These force fields yielded quite accurate values for both density and viscosity, with CHARMM36 emerging as the most suitable for modeling ether-based liquid membranes, especially for subsequent studies on ion transport [5].

Kinetic Migration Barriers

Beyond equilibrium properties, force fields can show starkly different performances when predicting kinetic barriers, which are governed by high-energy, rarely sampled states.

• In a study on Cr-intercalated Sbâ‚‚Te₃, a specialist MACE model trained from scratch on 20,000 configurations catastrophically failed, overestimating a key migration energy barrier by over 4 eV compared to the DFT-calculated barrier of 0.34 eV. This highlights a classic failure of extrapolation [26].
• A generalist MACE foundation model performed better, capturing the correct shape of the energy pathway but still overestimating the barrier by approximately 0.7 eV, a significant error that could alter conclusions about reaction rates [26].
• Fine-tuning the foundation model with a small amount (5%) of targeted, task-specific data resulted in a dramatic improvement, demonstrating that the choice of training strategy is as crucial as the choice of force field architecture itself [26].

NMR Observables and Secondary Structure

For biomolecular systems, agreement with Nuclear Magnetic Resonance (NMR) data is a key benchmark.

• The ff99SB force field has shown excellent agreement with experimental NMR order parameters and residual dipolar couplings for proteins like ubiquitin [25].
• However, its performance on short polyalanine peptides (Ala₃ and Alaâ‚…) is more nuanced. When evaluated using J-coupling constants, the force field, in combination with the TIP4P-Ew water model, ranks among the best available, though its ensemble shows a slight shift away from favored polyproline II (PPII) conformations towards more β-like conformations [25].
• This case also underscores the impact of ancillary choices; the water model (TIP3P vs. TIP4P-Ew) and the selection of Karplus parameters for converting dihedral angles to J-couplings can measurably affect the agreement with experiment [25].

Experimental Protocols for Benchmarking

To ensure reproducible and meaningful comparisons, researchers should adhere to detailed experimental protocols. The following methodologies are adapted from the studies cited in this guide.

Molecular Dynamics for Transport Properties

Objective: To calculate the equilibrium density and shear viscosity of a liquid (e.g., Diisopropyl Ether) across a temperature range [5].

• System Preparation: Construct initial configurations (e.g., 64 cubic unit cells with 3375 DIPE molecules for density calculations). For viscosity, use multiple independent cells to improve statistics [5].
• Simulation Details:
  • Software: GROMACS, LAMMPS, or similar MD packages.
  • Ensemble: Use the NpT ensemble for density calculations to allow volume change. For shear viscosity, the NVT ensemble is typically used.
  • Thermostat/Barostat: Employ a Nosé-Hoover thermostat and barostat for reliable temperature and pressure control.
  • Integration Time Step: 1-2 fs.
  • Production Run: After thorough energy minimization and equilibration, run production simulations for a sufficient duration (e.g., >50 ns) to achieve converged properties.
• Property Calculation:
  • Density: Calculate directly as the average mass per volume over the production trajectory.
  • Shear Viscosity: Compute using the Green-Kubo relation, which integrates the stress autocorrelation function, or via the non-equilibrium Einstein-Haddock method.

NMR Observable Validation

Objective: To validate a biomolecular force field by comparing simulated NMR observables, such as J-coupling constants, against experimental data [25].

• System Setup:
  • Peptide Solvation: Solvate the peptide (e.g., Alaâ‚…) in a water box (e.g., TIP3P, TIP4P-Ew) with a minimum distance between the peptide and box edge.
  • Ion Addition: Add ions to neutralize the system's charge.
• Simulation Details:
  • Enhanced Sampling: For small, floppy peptides, use replica-exchange molecular dynamics (REMD) to achieve adequate conformational sampling.
  • Simulation Length: Run simulations for a sufficient time per replica (e.g., 50 ns/replica) to ensure convergence of the conformational ensemble.
• Data Analysis:
  • Trajectory Analysis: From the simulation trajectory, extract a large ensemble of backbone dihedral angles (Ï•, ψ).
  • J-Coupling Calculation: Convert the dihedral angles into J-coupling constants using empirical Karplus equations (e.g., DFT1, DFT2, or "Original" parameter sets) [25].
  • Validation Metric: Calculate a χ² value that quantifies the sum of deviations between each calculated J-coupling constant and its experimental value, normalized by assumed systematic error [25].

Migration Barrier Calculation

Objective: To evaluate a force field's ability to predict energy barriers for atomic migration, a stringent test of its extrapolation capability [26].

• Reference Data Generation:
  • Use Density Functional Theory (DFT) to calculate the minimum energy pathway (MEP) for the migration event using the Nudged Elastic Band (NEB) method. This serves as the ground truth.
• Force Field Evaluation:
  • Single-Point Energy Calculation: Using the fixed geometric images from the DFT-NEB trajectory, perform single-point energy calculations with the machine-learned or classical force field.
  • Decoupling Energetics from Relaxation: This step isolates the model's accuracy in representing the potential energy surface from its structural relaxation behavior [26].
• Analysis:
  • Compare the energy profile and the predicted migration barrier (Eₐ) from the force field directly against the DFT reference.

Visualizing Benchmarking Relationships and Workflows

Force Field Benchmarking Framework

This diagram illustrates the logical framework and primary relationships involved in a systematic force field benchmarking study, connecting material systems with the properties used for evaluation.

Force Field Selection Logic

This workflow guides researchers through the critical decision-making process of selecting and applying a force field, highlighting the potential for discrepancies and mitigation strategies.

The Scientist's Toolkit

This section details essential computational reagents and resources used in force field benchmarking studies.

Research Reagent Solutions

Tool Name	Type	Primary Function	Key Application in Benchmarking
CHARMM36	Classical Force Field	Models biomolecules and organic liquids.	Accurate prediction of density and viscosity for ether-based liquid membranes [5].
GAFF	Classical Force Field	General model for organic molecules.	Serves as a baseline; often shows deviations in transport properties [5].
ff99SB	Classical Force Field	Specialized for protein simulations.	Validation against NMR observables for peptides and proteins [25].
MACE	Machine-Learning Force Field	Architecture for high-dimensional neural network potentials.	Benchmarking specialist vs. generalist models for solid-state materials [26].
Nudged Elastic Band	Computational Algorithm	Finds minimum energy paths and transition states.	Probing kinetic migration barriers to test force field extrapolation [26].
Green-Kubo Formalism	Mathematical Relation	Calculates transport properties from equilibrium MD.	Computing shear viscosity from stress autocorrelation functions [5].
Karplus Equations	Empirical Relation	Converts dihedral angles to NMR J-couplings.	Validating conformational ensembles from biomolecular simulations [25].
UniFFBench	Benchmarking Framework	Evaluates force fields against experimental data.	Systematic testing of universal MLFFs on mineral structures [27].
1,2-Dioleoyl-3-linoleoyl-rac-glycerol	1,2-Dioleoyl-3-linoleoyl-rac-glycerol, MF:C57H102O6, MW:883.4 g/mol	Chemical Reagent	Bench Chemicals
11-Dehydroxyisomogroside V	11-Dehydroxyisomogroside V, MF:C60H102O29, MW:1287.4 g/mol	Chemical Reagent	Bench Chemicals

Methodologies for Benchmarking Force Fields Across Material Systems

The development of high-performance solid polymer electrolytes (SPEs) is pivotal for advancing safe, energy-dense batteries. Understanding the intricate relationship between molecular structure, ion transport mechanisms, and macroscopic properties represents a fundamental challenge in this field. Molecular dynamics (MD) simulations have emerged as a powerful tool for probing these structure-transport relationships at the molecular level, enabling computational screening and design of novel materials. However, the accuracy of these simulations critically depends on the choice of force fields and simulation methodologies. This guide establishes a comprehensive benchmarking framework for evaluating classical force fields in predicting lithium-ion transport properties, providing researchers with standardized protocols for assessing simulation accuracy against experimental data. The framework addresses key aspects including force field parameterization, convergence criteria, and the impact of dynamic bonding phenomena on transport mechanisms.

Force Field Benchmarking: Methodologies and Protocols

Force Field Parameterization and Charge Scaling

Accurate force field parameterization is foundational for reliable MD simulations of polymer electrolytes. A critical finding across multiple studies is that non-polarizable force fields systematically overestimate ion-polymer binding energies when using formal ion charges, necessitating empirical charge scaling to achieve agreement with experimental diffusivity measurements.

Charge Scaling Protocol: For lithium ions (Li⁺), systematic parameter optimization against first-principles quantum-mechanical calculations justifies a charge scaling factor of approximately 0.79 for the OPLS force field applied to Li⁺-TFSI⁻-PEO systems [28]. This scaling factor emerges consistently across different Li⁺:EO ratios (1:10 and 1:20) and temperatures (300-373 K), demonstrating transferability within poly(ethylene oxide)-based electrolytes [28]. The parameter optimization process employs force-matching techniques that iteratively refine parameters to minimize the difference between force field forces and reference quantum-mechanical forces, typically achieving objective functions of 10-12% upon convergence [28].

Van der Waals Parameter Optimization: Concurrent optimization of Lennard-Jones parameters for Li-O (PEO) and Li-O (TFSI⁻) interactions is essential, with optimized values of σ~2.40-2.42 Å and ε~0.05-0.06 kcal/mol for Li-O(PEO) and σ~2.31-2.33 Å and ε~0.07 kcal/mol for Li-O(TFSI⁻) [28]. These refined parameters complement charge scaling to accurately capture ion coordination and dynamics.

Table 1: Optimized Force Field Parameters for Li⁺-TFSI⁻-PEO Systems

Parameter	Original OPLS	Optimized Value	Convergence Objective
Li⁺ Charge Scaling	1.0	0.79	10.7-10.9%
σ Li-O(PEO) (Å)	2.48	2.40-2.42	10.7-10.9%
ε Li-O(PEO) (kcal/mol)	0.05	0.05-0.06	10.7-10.9%
σ Li-O(TFSI⁻) (Å)	2.51	2.31-2.33	10.7-10.9%
ε Li-O(TFSI⁻) (kcal/mol)	0.06	0.07	10.7-10.9%

Simulation Convergence and Time Scales

MD simulations of polymer electrolytes require careful attention to convergence, as ion transport in these viscoelastic materials occurs over extended time scales. Benchmarking studies indicate that simulations spanning several hundreds of nanoseconds are necessary to approach the diffusive regime for Li⁺, even at elevated temperatures [28]. The convergence of transport properties should be systematically evaluated by monitoring the mean-squared displacement (MSD) of ions as a function of simulation time, ensuring linear behavior indicative of diffusive transport.

The diffusion coefficient (D) is calculated from the linear portion of the MSD versus time plot using the Einstein relation: $$D = \frac{1}{6Nt} \left\langle \sum{i=1}^{N} [ri(t) - r_i(0)]^2 \right\rangle$$ where N is the number of ions, ráµ¢(t) is the position of ion i at time t, and the angle brackets denote ensemble averaging [29]. Statistical uncertainty should be quantified through block averaging or multiple independent simulations.

Dynamic Bonding and Novel Transport Mechanisms

Beyond conventional PEO-based electrolytes, recent research has uncovered unique ion transport mechanisms in dynamic covalent adaptable networks (CANs). These systems exhibit fundamentally different structure-transport relationships compared to static polymer networks.

In CANs featuring dynamic disulfide bonds, bond exchange reactions create temporary "corridors" for lithium-ion movement through reversible bond breaking and reformation [29]. This dynamic bonding transforms blocked pathways into reversible gates that open and close, enhancing ion mobility up to 2.8-fold in dense networks without altering overall pore distribution [29]. Simulation protocols for these systems require specialized reactive force fields capable of modeling bond exchange events with user-defined exchange probabilities (P_exchange) that control the frequency of dynamic bond exchange [29].

Quantitative Benchmarking Data

Force Field Performance Comparison

Systematic benchmarking across 19 polymer electrolytes reveals the capabilities and limitations of Class 1 force fields in predicting transport properties [30]. The accuracy of diffusion coefficient predictions varies significantly with force field parameterization, with charge-scaled force fields providing substantial improvements over unscaled counterparts.

Table 2: Force Field Performance in Predicting Li⁺ Diffusivity

Force Field Type	Li⁺ Diffusion Coefficient	Deviation from Experiment	Optimal Application Conditions
Unscaled OPLS (~1.0e)	Underestimated by ~1 order of magnitude	>80% error	Not recommended for quantitative predictions
Charge-Scaled OPLS (~0.79e)	Slight underestimation	20-30% error	Li⁺:EO ratios 1:10 to 1:20; 300-373 K
Polarizable Force Fields	Closest to experimental values	<15% error	When computational resources permit

Structure-Transport Relationships Across Polymer Chemistries

The benchmarking framework enables comparative analysis of transport properties across diverse polymer chemistries, revealing clear structure-property relationships.

Table 3: Performance Metrics of Selected Polymer Electrolytes

Polymer Electrolyte	Ionic Conductivity	Li⁺ Transference Number	Activation Energy	Reference
PEO (benchmark)	~1 mS cm⁻¹ at 353 K	~0.2	~8 kJ/mol	[31]
ZAF-PEO Composite	1.37 mS cm⁻¹ at 333 K	0.56	Not reported	[32]
Dynamic CANs (disulfide)	Up to 2.8× enhancement vs static	Not reported	Reduced in dense networks	[29]
High-Conductivity Generative Designs	>0.506 mS cm⁻¹ (top 5%)	Varies	Varies by chemistry	[31]

The incorporation of zinc-adeninate frameworks (ZAF) into PEO demonstrates how additional hopping sites from carbonyl and hydrogen-bonding functionalities enhance both ionic conductivity (1.37 mS cm⁻¹ at 60°C) and lithium-ion transfer number (0.56) [32]. This represents a significant improvement over conventional PEO, which typically exhibits transference numbers of approximately 0.2 [31].

Experimental and Computational Workflows

Molecular Dynamics Simulation Protocol

Standardized MD protocols enable reproducible benchmarking across different research groups and polymer systems:

System Preparation:

• Construct polymer chains with specified molecular weights (typically below entanglement MW ~2000 g/mol for PEO)
• Incorporate salt species at target Li⁺:EO ratios (e.g., 1:10 to 1:20)
• Employ periodic boundary conditions in all dimensions
• Utilize energy minimization (steepest descent/conjugate gradient) prior to production runs

Equilibration Protocol:

• NPT equilibration using Parrinello-Rahman barostat (1 bar) and V-rescale thermostat (target temperature)
• Minimum 100 ns equilibration for sufficient chain relaxation
• Monitor convergence of energy, density, and structural properties

Production Simulation:

• Extended simulations (several hundred nanoseconds) to ensure diffusive regime
• Time steps of 1-2 fs for atomistic simulations, 10 fs for coarse-grained
• Trajectory saving intervals of 10-100 ps for subsequent analysis

Analysis Methods:

• Mean-squared displacement calculations for diffusion coefficients
• Radial distribution functions for ion coordination environments
• Van Hove correlation functions for collective ion behavior
• Pore size distribution analysis using tools like PoreBlazer [29]

Reactive Simulation for Dynamic Networks

For CANs with dynamic bonds, specialized reactive MD protocols are required:

Reactive Framework: Implement reactive MD tools like PolySMart built on Martini 3 force field for coarse-grained simulations [29]

Bond Exchange Algorithm:

• Identify disulfide groups within cutoff distance (typically 0.412 nm)
• Generate list of eligible bond pairs for exchange
• Apply exchange probability (P_exchange) to randomly select bonds for exchange
• Update topology information following exchange events

Multi-scale Validation:

• Reverse mapping from coarse-grained to atomistic representations
• Validation of structural and diffusional properties across scales
• Comparison with experimental measurements when available

Visualization of Methodologies and Relationships

Force Field Optimization Workflow

Ion Transport Mechanisms in Dynamic Networks

Research Reagent Solutions Toolkit

Table 4: Essential Computational Tools for Polymer Electrolyte Benchmarking

Tool/Software	Primary Function	Application Context	Key Features
GROMACS	Molecular Dynamics Engine	Production MD simulations of polymer electrolytes	Optimized for biomolecular/polymer systems, free energy calculations
PolySMart	Reactive MD Framework	Modeling dynamic covalent bonds in CANs	Python package for polymerization and crosslinking reactions
PoreBlazer v4.0	Pore Structure Analysis	Quantifying pore size distribution in polymer networks	Calculates PLD, MPD, and PSD parameters
OPLS-AA	Force Field	Classical MD with optimized Li⁺ parameters	Transferable parameters for organic molecules and polymers
Martini 3	Coarse-Grained Force Field	Large-scale and long-time simulations	Compatible with reactive MD schemes
Cimigenoside (Standard)	Cimigenoside (Standard), MF:C35H56O9, MW:620.8 g/mol	Chemical Reagent	Bench Chemicals
L,L-Dityrosine Hydrochloride	L,L-Dityrosine Hydrochloride, MF:C18H22Cl2N2O6, MW:433.3 g/mol	Chemical Reagent	Bench Chemicals

This benchmarking framework establishes standardized methodologies for evaluating force field performance in predicting structure-transport relationships of polymer electrolytes. The critical importance of charge scaling (approximately 0.79 for Li⁺) and optimized van der Waals parameters emerges as a consistent finding across multiple studies, with charge-scaled force fields improving agreement with experimental diffusivity by approximately one order of magnitude compared to unscaled force fields. Beyond conventional electrolytes, the framework accommodates emerging materials including dynamic covalent adaptable networks, which exhibit unique transport mechanisms mediated by reversible bond exchange. The integration of computational screening approaches with generative machine learning models presents a promising direction for accelerating the discovery of novel polymer electrolytes with enhanced ionic conductivity and mechanical properties. As the field advances, this benchmarking framework provides a foundation for rigorous, reproducible evaluation of simulation methodologies across diverse polymer chemistries and transport phenomena.

Simulating Ionic Liquids and Complex Charged Fluids with Neural Network Force Fields

The accurate simulation of ionic liquids and other complex charged fluids is pivotal for advancing technologies in energy storage, drug development, and materials science. Traditional molecular dynamics (MD) simulations relying on classical, parameterized force fields (FFs) have long struggled to balance computational efficiency with quantum mechanical accuracy, particularly in describing transport properties, polarization effects, and reactive processes [33] [34]. The emergence of machine learning force fields (MLFFs) marks a transformative development, offering the potential to perform large-scale molecular dynamics simulations with density functional theory (DFT) level accuracy [35] [36]. This guide provides a comparative analysis of current neural network force field (NNFF) methodologies, evaluating their performance against classical and ab initio alternatives. We focus on benchmarking their capabilities for predicting key properties—such as viscosity, ionic conductivity, and diffusion—within a broader thesis on computational transport properties research, providing researchers with the data and protocols needed to select appropriate tools for their specific applications.

Neural network force fields represent a paradigm shift from traditional FF design. Instead of using predefined mathematical forms with fitted parameters, NNFFs learn the complex relationship between atomic configurations and energies/forces directly from quantum mechanical data [34]. Several distinct architectural approaches have been developed:

• Bayesian-Based MLFFs: As applied to imidazolium-based ionic liquids, these methods successfully accelerate MD simulation while matching the accuracy of first-principles calculations for atomic forces, structures, and vibrational behaviors. They enable property prediction across extended scales of temperature and concentration [33].
• Deep Potential (DP) Schemes: Frameworks like the EMFF-2025 model for energetic materials demonstrate exceptional capabilities in modeling complex reactive chemical processes and large-scale system simulations, achieving DFT-level accuracy for both mechanical properties and chemical reactivity [35].
• Committee Neural Networks: Implemented in tools like NeuralIL, this approach uses multiple networks to estimate prediction uncertainty and can be iteratively refined with configurations from ML-MD simulations to significantly improve force prediction accuracy [34].
• Equivariant Architectures: Models such as Egret-1, based on the MACE architecture, incorporate physical symmetries (rotation, translation, permutation) directly into the network design, enhancing accuracy for organic and biomolecular systems [37].

Table 1: Key Neural Network Force Field Architectures for Charged Fluids

Architecture	Key Features	Representative Models	Target Systems
Bayesian MLFF	Accelerated calculation with uncertainty quantification	Bayesian-based MLFF [33]	Imidazolium-based ILs
Deep Potential	Scalable for large systems and reactive processes	EMFF-2025, DP-CHNO-2024 [35]	Energetic materials, CHNO systems
Committee Networks	Error estimation through network ensembles	NeuralIL [34]	Pure ILs, IL-salt mixtures
Equivariant Graph NN	Built-in physical symmetries	Egret-1 (MACE) [37]	Bioorganic molecules
Gaussian Approximation	Smooth Overlap of Atomic Position descriptors	GAP [36]	Molecular liquid mixtures

A critical challenge in applying NNFFs to molecular liquids is the separation of scale between intense intramolecular interactions and subtle intermolecular forces. As demonstrated in studies of EC:EMC binary solvents—key components of Li-ion batteries—NNFFs must simultaneously capture both interaction types to correctly predict thermodynamic properties like density [36]. Iterative training protocols that continuously refine the training dataset have proven essential for developing stable and accurate potentials for these systems.

Performance Benchmarking: Quantitative Comparisons

Accuracy Against Quantum Chemical Methods

NNFFs demonstrate remarkable accuracy approaching their DFT training data. The EMFF-2025 model for energetic materials exhibits mean absolute errors (MAE) predominantly within ±0.1 eV/atom for energy predictions and ±2 eV/Å for force calculations [35]. Similarly, NeuralIL replicates molecular structures of ionic liquids with bond lengths close to both OPLS-AA and DFT values, while significantly improving the prediction of weak hydrogen bond dynamics that are often poorly described by classical fixed-charge FFs [34].

Transport Property Prediction

Transport properties like viscosity and ionic conductivity present particular challenges for classical FFs, which often underpredict diffusion coefficients and conductivity due to inadequate treatment of polarization effects [34] [38]. NNFFs substantially improve upon these limitations:

Table 2: Performance Comparison for Imidazolium-Based Ionic Liquid [C4mim][BF4] at ~300K

Method Type	Specific Model	D+ (10⁻¹¹ m²/s)	D- (10⁻¹¹ m²/s)	Viscosity (mPa·s)	Conductivity (S/m)
Classical FF	OPLS-AA [19]	7.3	6.6	-	-
Polarizable FF	AMOEBA-IL [19]	2.9	0.67	-	-
Scaled-Charge FF	0.8*OPLS [19]	43.1	42.9	-	-
Machine Learning	ML Potential [19]	48.58	35.49	-	-
Experimental	-	8.0-40.0 [19]	8.2-47.6 [19]	-	0.295 [19]

NeuralIL correctly captures the dynamic properties of ionic liquids, producing mean square displacements, cage autocorrelation functions, and vibrational density of states that align with experimental observations and avoid the systematic errors of classical nonpolarized MD [34]. ML-based approaches have also been shown to successfully model proton transfer reactions, accurately predicting equilibrium coefficients for these processes [34].

System Size and Simulation Time Scaling

While NNFFs are typically 10-100 times slower than classical FFs, they offer orders-of-magnitude speedup compared to AIMD, making previously inaccessible simulations feasible [34]. For example, NeuralIL enables 100 ps-long ML-MD simulations of pure ILs and IL-inorganic salt mixtures with thousands of atoms at AIMD precision [34]. This balance of accuracy and efficiency allows researchers to study phenomena requiring longer timescales and larger systems while maintaining quantum mechanical accuracy.

Experimental and Simulation Protocols

Model Training Workflow

The development of robust NNFFs follows a systematic iterative process:

Key Benchmarking Experiments

Density Prediction in NPT Ensemble: The ability to maintain correct density during isothermal-isobaric (NPT) simulations serves as a sensitive test for intermolecular interaction quality [36]. Protocols involve:

• System: 128-512 ion pairs of target ionic liquid [34]
• Conditions: Multiple temperatures (300-400K) and 1 atm pressure
• Duration: Minimum 100 ps equilibration, 1-10 ns production [34]
• Validation: Compare against experimental density measurements and AIMD results

Transport Property Calculation:

• Diffusion: Calculate mean square displacement (MSD) of ions over 1-10 ns trajectories and apply Einstein relation: D = lim{t→∞} MSD/(6t) [38]
• Viscosity: Compute via Green-Kubo relation integrating pressure tensor autocorrelation function [33]
• Conductivity: Evaluate using Nernst-Einstein or direct current fluctuation methods [38]

Radial Distribution Function Analysis: Compare NNFF-predicted RDFs against AIMD and experimental scattering data to validate liquid microstructure [33] [34].

Research Reagent Solutions: Essential Tools

Table 3: Key Software Tools and Computational Resources

Tool Name	Type	Primary Function	System Compatibility
DeePMD-kit	Software Framework	Implementation of Deep Potential MD [35]	Linux, High-performance computing
NeuralIL	Specialized NNFF	Ionic liquid simulations with committee networks [34]	Linux, Python
EMFF-2025	Pretrained NNP	Energetic materials with CHNO elements [35]	Deep Potential compatible
DP-GEN	Automated Workflow	Generating ML potentials via active learning [35]	Linux, Python
Egret-1	Pretrained NNP	Bioorganic simulation based on MACE [37]	Python, PyTorch
QUANTUM ESPRESSO	DFT Code	Generating training data [34]	Linux, High-performance computing

Neural network force fields represent a significant advancement in simulating ionic liquids and complex charged fluids, effectively bridging the gap between computationally expensive ab initio methods and inaccurate classical force fields. Current benchmarks demonstrate that NNFFs can predict structural properties with DFT-level accuracy while accessing timescales necessary for reliable transport property calculation.

Despite these successes, challenges remain in achieving full transferability across diverse chemical systems, handling explicit long-range electrostatics efficiently, and further reducing computational overhead compared to classical FFs [34] [37]. The integration of active learning approaches, improved treatment of long-range interactions, and development of more specialized pretrained models represent promising directions for addressing these limitations. As NNFF methodologies continue to mature, they are poised to become indispensable tools for researchers investigating complex charged fluids in fields ranging from battery development to pharmaceutical design.

Molecular dynamics (MD) simulations provide an atomistic view of fluid transport through biological nanopores, offering insights that are often challenging to obtain experimentally [39]. The reliability of these simulations critically depends on the empirical force fields used to model atomic interactions. For electrohydrodynamic phenomena in nanopores—such as electroosmotic flow and ionic conductance—the choice of force field can significantly impact simulation outcomes, potentially leading to qualitatively different predictions [39]. This guide objectively compares the performance of two prominent force field families, AMBER and CHARMM, in simulating electrohydrodynamic properties of biological nanopores, providing researchers with a framework for selecting appropriate models for their specific applications.

Force Field Fundamentals and Electrohydrodynamics

Force Fields in Molecular Dynamics

Molecular Mechanics force fields are simplified classical models that enable simulations of biomolecular systems at relevant spatial and temporal scales [40]. They consist of a potential energy function and an associated parameter set that together calculate the energy and forces on a system based on its atomic coordinates [40]. In nanopore simulations, these force fields model the interactions between the pore protein, ions, and water molecules, directly influencing the predicted electrohydrodynamic behavior.

Electrohydrodynamics in Nanopores

Electrohydrodynamics encompasses fluid motion induced by electric fields [41]. In nanopore sensing, electroosmotic flow is particularly relevant—it occurs when counterions accumulated near charged pore surfaces drag water molecules along under an external electric field [39]. This phenomenon enables the capture of molecules regardless of their net charge and is pivotal for sensing applications [39]. Accurate computational prediction of EOF is challenging yet essential, as direct experimental measurements in biological nanopores are not feasible [39].

Comparative Analysis of AMBER and CHARMM Force Fields

Force Field Specifications and Compatible Water Models

The table below summarizes key characteristics of the latest AMBER and CHARMM force fields relevant to electrohydrodynamic simulations:

Table 1: Force Field and Water Model Specifications

Force Field	Compatible Water Models	Electrostatic Treatment	Key Features for Nanopore Simulations
AMBER-ff14SB	TIP3P [39]	Additive (fixed charges) [39]	Balanced protein parameters; often used with CUFIX ion corrections [39]
AMBER-ff19SB	OPC [39]	Additive (fixed charges) [39]	Improved backbone torsion potentials; paired with higher-viscosity OPC water [39]
CHARMM36	Modified TIP3P [39]	Additive (fixed charges) [39] [40]	Optimized for phospholipids & proteins; includes CMAP corrections [40]
CHARMM Drude	SWM4-NDP [40]	Polarizable (Drude oscillator) [40]	Explicitly models electronic polarization; more accurate for heterogeneous dielectric environments [40]

Performance Comparison in Electrohydrodynamic Properties

Recent systematic comparisons of force fields in simulating biological nanopores (CytK and MspA) reveal both consistencies and critical differences:

Table 2: Electrohydrodynamic Performance Comparison

Performance Metric	AMBER-ff14SB	AMBER-ff19SB	CHARMM36	Experimental Reference
Cation/Anion Selectivity Direction	Consistent across force fields [39]	Consistent across force fields [39]	Consistent across force fields [39]	N/A
Electroosmotic Flow Direction	Coherent across force fields [39]	Coherent across force fields [39]	Coherent across force fields [39]	N/A
Quantitative EOF Rate	Intermediate [39]	Lower (due to higher viscosity OPC water) [39]	Higher [39]	Not directly measurable
Ionic Current Magnitude	Varies significantly between force fields [39]	Varies significantly between force fields [39]	Varies significantly between force fields [39]	Measurable experimentally
Narrow Pore (MspA) Predictions	May show detectable EOF [39]	May predict no detectable EOF [39]	Qualitative differences possible [39]	Method-dependent estimation

Water Model Implications

The choice of water model profoundly impacts electrohydrodynamic predictions. The OPC water model used with AMBER-ff19SB has a viscosity approximately 2.5-fold higher than the TIP3P model used with CHARMM36 and AMBER-ff14SB [39]. This difference directly affects electroosmotic flow rates and ionic mobility. OPC's viscosity is more similar to experimental water, but TIP3P's lower viscosity may artificially enhance flow rates in simulations [39].

Experimental Protocols and Methodologies

Standard Simulation Protocol for Nanopore Electrohydrodynamics

The methodology below, adapted from recent comparative studies, ensures consistent evaluation of force field performance:

Figure 1: Simulation workflow for nanopore electrohydrodynamics

System Setup and Equilibration

• Nanopore Preparation: Obtain protein structures from databases (e.g., OPM). Align the pore axis with the z-axis of the coordinate system. For mutant studies, introduce point mutations using molecular visualization software [39].
• Membrane Embedding: Embed the nanopore in a POPC lipid bilayer using automated membrane generation tools. Remove lipid molecules that overlap with the protein or pore lumen [39].
• Solvation and Ionization: Add water molecules using the appropriate model (TIP3P for CHARMM36/ff14SB; OPC for ff19SB). Add ions to achieve physiological concentration (typically 0.1-1M KCl) and neutralize system charge [39].
• Energy Minimization: Perform 5,000 steps of energy minimization to remove steric clashes [39].
• Membrane Equilibration: Conduct a 494 ps NPT equilibration with positional restraints on protein Cα atoms and lipid phosphorus atoms. Apply external forces to prevent water penetration into the membrane during initial relaxation. Implement a temperature ramp from 0K to 300K for smooth system relaxation [39].

Production Simulations and Analysis

• Nonequilibrium MD: Apply an external electric field corresponding to ΔV = 0.1-1V using Ez = ΔV/Lz, where Lz is the box length along the pore axis [39].
• Simulation Parameters: Use a 2.0 fs time step with bond constraints. Employ particle mesh Ewald for long-range electrostatics with a 12Ã… cutoff. Use a Langevin thermostat for temperature control (300K) and Nosé-Hoover Langevin piston for pressure control (1 atm) [39].
• Current Calculation: Calculate ionic current I(t) using the equation I(t) = (1/Ï„Lz) × Σqi[zi(t+Ï„)-zi(t)], where Ï„ is the trajectory output interval (typically 20ps), qi is the ion charge, and zi is its position [39].
• Electroosmotic Flow Measurement: Track water molecule displacement along the pore axis under the applied electric field. Compute net flow rates by separating cation and anion contributions to the total current [39].

Key Performance Metrics

When benchmarking force fields for electrohydrodynamic properties, researchers should evaluate:

• Ionic Current Accuracy: Compare simulated current magnitudes with experimental measurements where available.
• Electroosmotic Flow Rate: Quantify water transport per unit charge.
• Selectivity Ratio: Calculate cation/anion permeability ratios from reversal potentials or current composition analysis.
• Convergence Behavior: Monitor the stability of these metrics over simulation time to ensure sufficient sampling.

Table 3: Essential Resources for Nanopore Electrohydrodynamics Research

Resource Category	Specific Examples	Function/Purpose
Simulation Software	NAMD [39], CHARMM [42]	MD simulation engines with electrostatics and periodic boundary implementations
Force Fields	AMBER-ff19SB [39], CHARMM36 [39] [40], CHARMM Drude [40]	Parameter sets defining atomic interactions and properties
Water Models	TIP3P [39], OPC [39], SWM4-NDP [40]	Solvent models with varying dielectric and viscosity properties
System Building Tools	VMD Solvate Package [39], VMD Autoionize [39]	Software utilities for constructing membrane-protein systems and adding solvents/ions
Analysis Methods	Current Calculation [39], Flow Analysis [39]	Algorithms for quantifying ionic current and electroosmotic flow from trajectories
Experimental Validation	Ionic Conductance [39], Selectivity Measurements [39]	Indirect experimental metrics for validating simulation predictions

The comparative analysis of AMBER and CHARMM force fields reveals that while both families generally agree on qualitative trends in ion selectivity and electroosmotic flow direction, they exhibit significant quantitative differences in simulated ionic currents and flow rates [39]. These discrepancies stem from variations in protein-ion interactions and the choice of water model, particularly the substantial viscosity differences between TIP3P and OPC models [39].

For researchers studying biological nanopores, these findings highlight the importance of:

• Force Field Selection: Choose based on the specific electrohydrodynamic property of interest.
• Consistent Methodology: Maintain identical simulation parameters when comparing between systems.
• Water Model Consideration: Account for viscosity effects when interpreting flow rates.
• System-Specific Validation: Where possible, validate against experimental ionic current measurements.

The ongoing development of polarizable force fields like CHARMM Drude offers promise for more accurate electrohydrodynamic simulations, particularly in heterogeneous dielectric environments like nanopore-membrane systems [40]. As force fields continue to evolve, their increasing physical accuracy will enhance the predictive power of molecular dynamics for nanopore-based sensing and separation technologies.

The development of accurate force fields is a cornerstone of computational materials science and drug development. Machine-learned force fields (MLFFs) now enable molecular dynamics (MD) simulations with near-first-principles accuracy at significantly larger scales. A pivotal dilemma facing researchers is the choice between developing bespoke, system-specific specialist models or adapting large, pre-trained generalist foundation models. Understanding the trade-offs in their performance, particularly for predicting transport properties and non-equilibrium processes, is crucial for reliable simulations. This guide objectively benchmarks these competing approaches, using advanced non-equilibrium diagnostic probes to provide a clear comparison for practitioners [26] [43].

The critical challenge in benchmarking lies in moving beyond equilibrium properties. While many models accurately capture static structures, their performance often diverges dramatically when simulating kinetic processes like atomic migration or diffusion. These processes dictate material functionality and drug efficacy but involve high-energy, rare events that are poorly sampled in standard training data. This comparison employs migration pathways, evaluated via nudged elastic band (NEB) calculations, as a stringent diagnostic probe to test the interpolation and extrapolation capabilities of different MLFF training strategies [26] [44].

Methodological Framework: Benchmarking with Diagnostic Probes

Core Benchmarking Workflow

A robust benchmark requires a structured workflow that assesses models across multiple property domains. The following diagram illustrates the integrated framework used for this comparison, from model preparation to final assessment.

Experimental Protocols for Key Diagnostics

Molecular Dynamics for Equilibrium Properties

Purpose: To validate a model's ability to maintain a stable thermodynamic ensemble and reproduce key structural and dynamic properties over time [26] [2].

Protocol:

• Simulation Setup: Initialize the system (e.g., Cr-intercalated Sbâ‚‚Te₃ for materials or a protein-ligand complex for drug development) using coordinates from the model. Assign velocities corresponding to the target temperature (e.g., 300 K or 600 K).
• Production Run: Perform a sufficiently long MD simulation (e.g., 200 ps) using the MLFF to compute forces.
• Property Analysis:
  • Structural: Calculate the Radial Distribution Function (RDF) and compare it to reference ab initio MD (AIMD) data to validate local structure.
  • Dynamic: Analyze the Velocity Autocorrelation Function (VACF) to assess short-time dynamics.
  • Transport: Compute the diffusion coefficient from the mean squared displacement and evaluate thermal conductivity from heat flux correlations.

Interpretation: A successful model will maintain structural stability, show no drift in energy, and accurately reproduce reference transport coefficients [26] [2].

Nudged Elastic Band for Migration Pathways

Purpose: To stringently test the model's accuracy in predicting kinetic energy barriers by probing the potential energy surface (PES) far from equilibrium minima [26] [43].

Protocol:

• Path Initialization: Identify an initial and final state for the migration event (e.g., a dopant moving between interstitial sites). Generate an initial guess for the reaction path, often a linear interpolation.
• NEB Calculation: Use the NEB method to find the minimum energy path (MEP). Multiple "images" of the system are created along the path and optimized subject to spring forces between images and a force projection that ensures convergence to the MEP.
• Single-Point Validation: For a controlled assessment, the MEP from a reference DFT-NEB calculation can be used as a fixed geometric trajectory. The MLFF's energy for each image is then calculated as a single-point evaluation.
• Barrier Extraction: Identify the highest energy image along the path as the transition state and calculate the activation energy barrier, ( E_a ) [26].

Interpretation: This probe directly tests a model's ability to extrapolate. Poor models may severely overestimate the barrier (catastrophic failure) or yield a qualitatively correct but quantitatively inaccurate path (PES smoothing) [26].

Performance Comparison of MLFF Training Paradigms

Quantitative Performance Metrics

The following tables summarize the quantitative performance of different MLFF training strategies, benchmarked on a model system of Cr-doped Sb₂Te₃. Data is derived from a systematic study using the MACE architecture [26].

Table 1: Performance on Equilibrium and Transport Properties

Training Strategy	Force Error (meV/Ã…)	Energy Error (meV/atom)	Diffusion Coefficient (600K)	Thermal Conductivity
Specialist (From Scratch)	Low on training data	Low on training data	Lower than fine-tuned models	Sustains long-range correlations
Generalist (Zero-Shot)	Variable, system-dependent	Variable, system-dependent	Lower than fine-tuned models	Decays rapidly to zero
Fine-Tuned (FT-600K)	Reduced vs. zero-shot	Reduced vs. zero-shot	Higher	Anomalous peak, potential instability
Fine-Tuned (FT-MultiT)	Lowest on target data	Lowest on target data	Highest	Sustains long-range correlations

Table 2: Performance on Non-Equilibrium Kinetic Properties

Training Strategy	Migration Barrier Error	Extrapolation Reliability	Data Efficiency	Catastrophic Forgetting
Specialist (From Scratch)	Catastrophic (e.g., +4.0 eV)	Poor	Low (requires 10,000s of configurations)	Not Applicable
Generalist (Zero-Shot)	Large overestimation (e.g., +0.7 eV)	Moderate (qualitatively correct)	High (no data needed)	Not Applicable
Fine-Tuned (FT-600K)	Dramatically improved	Good for targeted task	Very High (effective with ~5% of data)	Observed for long-range physics
Fine-Tuned (FT-MultiT)	Best performance	Best overall	High	Mitigated

Analysis of Training Paradigms

The Specialist Model: From-Scratch Training

Specialist models are trained exclusively on a system-specific dataset. While they can achieve low error on the training distribution and capture some long-range correlations like thermal conductivity, they are highly prone to catastrophic failure when probed on non-equilibrium pathways. As shown in Table 2, a specialist model overestimated a key migration barrier by over 4 eV, a classic signature of overfitting to near-equilibrium states and a complete failure to extrapolate. This approach is also data-inefficient, often requiring tens of thousands of AIMD configurations [26].

The Generalist Model: Zero-Shot Foundation Model

Generalist foundation models (e.g., MACE-MP, CHGNet) are pre-trained on millions of diverse structures. They provide a qualitatively correct, smooth potential energy surface without any target system data, making them highly data-efficient. They can yield a plausible-looking migration pathway. However, as they are not specialized, they often "smooth over" specific details, leading to significant quantitative inaccuracies, such as overestimating migration barriers by ~0.7 eV. They may also fail to capture finite-temperature properties, indicated by a poor prediction of thermal conductivity [26] [43].

The Hybrid Approach: Fine-Tuned Foundation Model

Fine-tuning a foundation model on a small amount of system-specific data (e.g., 5% of a full dataset) combines the strengths of both paradigms. This strategy dramatically improves the prediction of kinetic barriers and transport properties, as shown in Table 2. The model learns system-specific details while retaining the general physical knowledge from pre-training. The primary risk is catastrophic forgetting, where the model loses accuracy on properties not represented in the fine-tuning dataset. Latent space analysis confirms that fine-tuning produces a fundamentally distinct model, not just a refined version of the foundation model [26] [43] [44].

The Scientist's Toolkit: Essential Research Reagents

Table 3: Key Software and Computational Tools for MLFF Development

Item	Function/Brief Explanation
MACE Architecture	A state-of-the-art machine learning architecture used for building high-accuracy MLFFs, supporting both from-scratch training and fine-tuning [26] [43].
VASP/Quantum ESPRESSO	First-principles electronic structure codes (DFT) used to generate the reference ab initio molecular dynamics (AIMD) data required for training and validating MLFFs [26].
ASE (Atomic Simulation Environment)	A Python package used to set up, run, and analyze MD and NEB calculations, interfacing with both DFT codes and MLFFs [26].
LAMMPS/i-PI	Molecular dynamics simulation engines that can be integrated with MLFFs to run large-scale and long-time-scale MD simulations [26].
Nudged Elastic Band (NEB)	An algorithm for finding the minimum energy path and energy barrier for atomic migration or chemical reactions [26].
Methyl pyropheophorbide-a	Methyl pyropheophorbide-a, MF:C34H36N4O3, MW:548.7 g/mol

This guide demonstrates that the choice of MLFF strategy involves a direct trade-off between data efficiency and robust generalizability. For researchers whose primary concern is the accurate prediction of kinetic rates and transport properties, targeted fine-tuning of a generalist model is the most effective path, provided the fine-tuning dataset is carefully curated to include relevant non-equilibrium states. However, for applications where long-range physical correlations are critical, a comprehensive from-scratch training with extensive data may still be necessary, despite its high cost and risk of extrapolation error. The use of migration pathways as a diagnostic probe is a powerful and necessary practice to reveal these critical performance differences that equilibrium benchmarks alone cannot detect [26] [43] [44].

The accuracy of high-throughput screening (HTS) for computational material discovery depends critically on the force fields that govern interatomic interactions in molecular dynamics (MD) simulations. Force fields are mathematical models that calculate the potential energy of a molecular system based on nuclear coordinates, enabling the prediction of material properties and behaviors [45]. As HTS approaches expand to evaluate thousands of materials in silico, selecting appropriate force fields becomes paramount for generating reliable, experimentally valid data. This guide provides an objective comparison of force field performance across material classes, with particular emphasis on predicting transport properties—critical metrics for applications ranging from drug design to membrane development and energy materials.

The fundamental challenge in computational material discovery lies in the transferability and accuracy of empirical force fields. While molecular dynamics simulations can capture behavior of proteins and other biomolecules in full atomic detail at fine temporal resolution, the results depend entirely on the force field's quality [45]. Recent advances in computing hardware, particularly graphics processing units (GPUs), have made nanosecond to microsecond simulations accessible to more researchers, elevating the importance of force field selection rather than computational resources as the primary constraint for accurate high-throughput discovery [45].

Comparative Analysis of Force Field Performance

Performance Across Material Systems

Table 1: Force Field Performance for Structural and Transport Properties

Material System	Top-Performing Force Fields	Validated Properties	Experimental Agreement	Key Limitations
Polyamide Membranes	CVFF, SwissParam, CGenFF [46]	Dry density, porosity, pore size, Young's modulus, water permeability [46]	Pure water permeability within 95% experimental CI [46]	Limited validation for ion transport properties
CaO-Al₂O₃-SiO₂ Melts	Bouhadja et al. [2]	Density, bond lengths, coordination numbers, self-diffusion coefficients, electrical conductivity [2]	Accurate activation energies; robust transferability beyond parameterization range [2]	Variable performance for Si-O tetrahedral environments
Lubricants (n-hexadecane)	L-OPLS-AA (all-atom) [1]	Density, viscosity, structure, friction coefficients [1]	Quantitative agreement with experimental friction behavior [1]	United-atom variants significantly under-predict viscosity
Organometallic Crystals	Machine Learning Force Fields [47]	Thermal conductivity [47]	0.49 W m⁻¹ K⁻¹ vs. experimental 0.39 W m⁻¹ K⁻¹ [47]	Requires substantial training data; computationally intensive

Quantitative Comparison of Transport Property Predictions

Table 2: Transport Property Accuracy Metrics Across Force Fields

Force Field	System Type	Diffusion Coefficient Error (%)	Viscosity Error (%)	Thermal Conductivity Error (%)	Electrical Conductivity Error (%)
Bouhadja et al.	Oxide Melts [2]	8-15	N/R	N/R	10-20
Matsui et al.	Oxide Melts [2]	20-40	N/R	N/R	30-50
Guillot et al.	Oxide Melts [2]	15-30	N/R	N/R	25-45
L-OPLS-AA	n-hexadecane [1]	5-12	8-15	N/R	N/R
United-Atom (TraPPE)	n-hexadecane [1]	25-40	40-60	N/R	N/R
Machine Learning (CuPc)	Organometallic [47]	N/R	N/R	~25	N/R

N/R: Not reported in the cited studies

Experimental Protocols for Force Field Benchmarking

Standardized Workflow for Transport Property Validation

The accuracy of force fields in predicting transport properties must be established through systematic benchmarking against experimental data and higher-level theoretical calculations. The following workflow provides a standardized protocol for validating force field performance across material systems:

Key Methodological Considerations

System Preparation and Equilibration

For polyamide membranes, successful benchmarking involves simulating membranes in both dry and hydrated states, with validation against experimentally synthesized membranes of similar chemical composition [46]. The membrane composition, particularly the O/N ratio and proportions of oxygen and nitrogen species, should be validated against experimental characterizations prior to transport property calculations [46]. For oxide melt systems, simulations should span the complete composition and temperature range of interest, typically covering 10+ compositions across temperatures ranging from 1400°C to 1600°C for industrial relevance [2].

Equilibration protocols must be rigorously validated through monitoring of energy stability and diffusion convergence. For accurate transport properties, systems should be equilibrated in the NPT ensemble to achieve experimental densities before switching to NVE or NVT ensembles for production runs [2] [1]. The equilibration duration should be sufficient to exceed the structural relaxation time of the system, typically 1-10 nanoseconds for complex molecular systems.

Transport Property Calculation Methods

Self-diffusion coefficients are most accurately calculated through Einstein's relation applied to mean squared displacement (MSD) of atoms over time [2]:

\[ D = \frac{1}{6} \lim{t \to \infty} \frac{d}{dt} \langle | \mathbf{r}i(t) - \mathbf{r}_i(0) |^2 \rangle \]

For viscosity calculations, the Green-Kubo formulation relates the viscosity to the integral of the stress autocorrelation function [1]:

\[ \eta = \frac{V}{kB T} \int0^\infty \langle P{\alpha\beta}(t) P{\alpha\beta}(0) \rangle dt \]

where \( P_{\alpha\beta} \) are the off-diagonal elements of the pressure tensor.

Thermal conductivity calculations for organometallic systems similarly employ Green-Kubo methods with heat current autocorrelation functions [47]:

\[ \kappa = \frac{V}{kB T^2} \int0^\infty \langle \mathbf{J}q(t) \cdot \mathbf{J}q(0) \rangle dt \]

where \( \mathbf{J}_q \) is the heat flux vector.

Electrical conductivity in ionic systems can be computed via the Nernst-Einstein relation using ion diffusivities [2] or through direct application of external electric fields in non-equilibrium MD simulations [46].

Table 3: Essential Computational Tools for High-Throughput Force Field Screening

Tool Category	Specific Solutions	Function	Application Examples
Force Field Libraries	GAFF, CVFF, PCFF, CGenFF, OPLS-AA [46] [1]	Provide parameter sets for diverse molecular systems	Organic molecules, polymers, biomolecules
Specialized Potentials	Bouhadja (oxide melts), Matsui (CMAS systems) [2]	Address specific material classes with optimized parameters	High-temperature melts, ceramic systems
MD Simulation Packages	LAMMPS, GROMACS, AMBER, CHARMM [1] [45]	Perform molecular dynamics calculations with various force fields	High-throughput screening across multiple systems
Analysis Tools	MDAnalysis [48], VMD, MDTraj	Process trajectories and calculate properties	RMSD, hydrogen bonding, diffusion coefficients
Validation Databases	NIST, ThermoML, Cambridge Structural Database	Provide experimental data for force field validation	Density, viscosity, thermal conductivity benchmarks
Machine Learning Potentials	MEHnet [49], Active Learning FF [47]	Achieve quantum-chemical accuracy at lower computational cost	Complex organometallics, excited states properties

Emerging Approaches and Future Directions

Machine Learning Force Fields

Recent advances in machine learning have enabled the development of force fields with quantum-chemical accuracy, particularly for complex systems where traditional force fields struggle. For organometallic complexes like copper phthalocyanine, active learning approaches combined with deep neural networks have demonstrated superior performance in predicting thermal transport properties compared to classical force fields, achieving thermal conductivity predictions of 0.49 W m⁻¹ K⁻¹ versus experimental values of 0.39 W m⁻¹ K⁻¹ [47].

The Multi-task Electronic Hamiltonian network (MEHnet) represents a significant advancement by enabling the prediction of multiple electronic properties—including dipole and quadrupole moments, electronic polarizability, and optical excitation gaps—from a single model trained on coupled-cluster theory [CCSD(T)] calculations [49]. This approach provides CCSD(T)-level accuracy, considered the gold standard in quantum chemistry, at computational costs potentially lower than conventional density functional theory (DFT) methods [49].

High-Throughput Screening Infrastructure

Effective HTS for computational material discovery requires integrated informatics platforms that manage the complete workflow from molecular structure generation to property calculation and validation. These systems should incorporate automated job submission, error recovery, and quality control metrics to handle the thousands of simulations required for comprehensive force field assessment.

Quality control procedures adapted from quantitative high-throughput screening (qHTS), such as Cluster Analysis by Subgroups using ANOVA (CASANOVA), can identify inconsistent response patterns across repeated simulations, flagging potentially unreliable results for further investigation [50]. For force field validation, this translates to monitoring property convergence across multiple independent simulations and different initial configurations.

Based on comprehensive benchmarking across material classes, the following recommendations emerge for force field selection in high-throughput screening of transport properties:

• For polymer membranes, CVFF, SwissParam, and CGenFF provide the most accurate predictions of water permeability and mechanical properties, with validation against experimental pure water permeability measurements essential [46].

• For oxide melt systems, Bouhadja's force field outperforms alternatives for both structural and dynamic properties, particularly for electrical conductivity predictions where it demonstrates 10-20% error versus experimental data [2].

• For organic lubricants and similar molecular fluids, all-atom force fields like L-OPLS-AA are strongly recommended over united-atom variants, which systematically under-predict viscosity by 40-60% [1].

• For complex organometallic systems, machine learning force fields now offer superior accuracy for thermal transport properties, though require substantial training data and computational resources for development [47].

The field continues to evolve rapidly, with machine learning approaches promising to extend quantum-chemical accuracy to increasingly complex materials systems. As these methods mature, they will likely become integrated into standard HTS workflows for computational material discovery, enabling more reliable in silico screening of novel materials with tailored transport properties.

Addressing Pathologies and Optimizing Force Field Performance

Correcting Systematic Deficiencies in Classical Force Fields

Classical molecular dynamics (MD) simulations are a cornerstone of modern computational chemistry, materials science, and drug discovery, enabling researchers to investigate atomic-scale processes that are inaccessible to experimental observation. The accuracy of these simulations, however, is fundamentally dependent on the quality of the underlying force fields—mathematical representations of the potential energy surface that governs atomic interactions. Despite decades of refinement, systematic deficiencies in classical force fields persist, limiting their predictive power for key physicochemical properties, particularly transport properties such as diffusion coefficients and electrical conductivity [2] [16].

The development of force fields has historically faced a challenge known as the "transferability-accuracy trade-off." Traditional parameterization approaches often prioritized transferability across diverse chemical systems, sometimes at the expense of quantitative accuracy for specific properties [51]. Furthermore, many widely used force fields employ simplified functional forms, such as the Lennard-Jones potential and fixed-charge electrostatics, which cannot fully capture complex many-body electronic effects like polarization, charge transfer, and anisotropic electron distribution [16] [52] [53]. These limitations become particularly pronounced when simulating dynamic processes in complex, charged fluids or when attempting to predict properties far from the original parameterization conditions.

This guide provides a comparative analysis of contemporary strategies for identifying and correcting systematic force field deficiencies, with a specific focus on benchmarking transport properties. By evaluating traditional empirical potentials against emerging machine-learning alternatives and detailing robust validation methodologies, we aim to equip researchers with the knowledge needed to select and develop force fields with enhanced predictive accuracy.

Methodologies for Benchmarking Force Field Performance

Standardized Protocols for Property Validation

A systematic benchmarking study requires a standardized protocol for comparing force field predictions against reliable reference data. The following properties are typically assessed to evaluate both structural and dynamic accuracy:

• Structural Properties: Density, radial distribution functions (RDFs), bond lengths, and coordination numbers are fundamental metrics. These should be validated against experimental data or high-level ab initio molecular dynamics (AIMD) simulations [2].
• Transport Properties: Self-diffusion coefficients, viscosity, and electrical conductivity are critical dynamic metrics. Accurate prediction of these properties, including their temperature dependence (activation energies), is a stringent test of a force field's quality [2] [16].
• System Composition and Conditions: Benchmarking must be performed across a wide range of compositions and temperatures to assess transferability. For instance, a robust study on CaO-Alâ‚‚O₃-SiOâ‚‚ melts should span ten compositions and temperatures from 1400–1600°C [2].

The choice of reference data is crucial for meaningful validation:

• Experimental Data: The ultimate benchmark for properties like density and viscosity [2].
• Ab Initio MD (AIMD): Provides atomistically detailed reference data for structural properties where experiments are challenging. While computationally too expensive for long-timescale dynamics, AIMD offers a reliable benchmark for local structure [2] [16].
• CALPHAD Models: Established thermodynamic and property databases can provide additional reference points for properties like density [2].

The workflow below illustrates the interconnected stages of a comprehensive force field benchmarking study.

Comparative Analysis of Force Field Correction Strategies

Advancements in Traditional Empirical Force Fields

Ongoing refinement of traditional force fields remains a viable path to improving accuracy, focusing on more physically grounded parameterization and functional forms.

Table 1: Performance Comparison of Empirical Force Fields for Oxide Melts (CaO-Al₂O₃-SiO₂)

Force Field	Density & Si-O Structure	Al-O & Ca-O Bonding	Self-Diffusion Coefficients	Electrical Conductivity	Transferability
Matsui et al.	Accurate prediction [2]	Less accurate vs. AIMD [2]	Lower accuracy [2]	Lower accuracy [2]	Limited [2]
Guillot & Sator	Accurate prediction [2]	Less accurate vs. AIMD [2]	Lower accuracy [2]	Lower accuracy [2]	Limited [2]
Bouhadja et al.	Accurate prediction [2]	Best agreement with AIMD [2]	Best agreement with experiment [2]	Best agreement with experiment [2]	Robust beyond parameterization range [2]

The PHAST 2.0 force field represents a significant shift in philosophy. It is parameterized solely on electronic structure data and incorporates explicit many-body polarization, moving away from the state-point dependent Lennard-Jones paradigm. This approach demonstrates that sub-kilojoule-per-mole accuracy can be achieved with minimal atom typing and enhanced transferability [52].

Emerging Machine Learning and Neural Network Force Fields

Machine learning force fields (MLFFs) represent a paradigm shift, learning the potential energy surface directly from quantum mechanical data without relying on pre-defined functional forms.

• NeuralIL: A neural network force field (NNFF) for ionic liquids demonstrates a capability to overcome pathological deficiencies of classical force fields. It accurately reproduces structural properties, weak hydrogen bond dynamics, and can even model proton transfer reactions, which are inaccessible to fixed-charge potentials [16].
• Performance Gains: MLFFs bridge the gap between the accuracy of AIMD and the computational efficiency of classical MD. They enable calculations with AIMD precision for systems of thousands of atoms and simulation times of hundreds of picoseconds, allowing for the accurate computation of transport properties that require long time scales [16].

Table 2: Strategy Comparison for Addressing Force Field Deficiencies

Strategy	Representative Example(s)	Approach to Polarization/Electrostatics	Key Advantage	Key Limitation
Reparameterization	Bouhadja et al. [2]	Improved fixed charges within Born-Mayer-Huggins potential	Improved accuracy for specific systems (e.g., melts)	Limited transferability; cannot capture electronic effects
Advanced Functional Forms	PHAST 2.0 [52], AMOEBA+ [53]	Explicit many-body polarization; multipole electrostatics	More physically rigorous description of interactions	Higher computational cost; complex parameterization
Machine Learning Potentials	NeuralIL [16]	Environment-dependent atomic energies/forces	DFT-level accuracy; no pre-defined functional form	High computational cost vs. classical MD; data hungry

Specialized Parameterization for Specific Properties

For properties that depend critically on high-order derivatives of the potential energy surface, such as phonon spectra, a specialized fitting procedure can yield high accuracy by sacrificing some transferability.

• Targeted Fitting: A valence force field (VFF) model with ~50 parameters can be automatically fitted to reproduce the ab initio phonon spectrum of CdSe nanostructures with high accuracy. This procedure uses a large number of parameters focused on accuracy for a specific class of systems rather than general transferability [51].
• Protocol: The fitting involves stages (bulk then surface), uses ab initio forces and energies, and carefully weights the data to avoid overfitting. While the parameters may not be uniquely determinable, the resulting model accurately reproduces the target phonon spectrum [51].

Table 3: Key Computational Tools for Force Field Development and Benchmarking

Tool / Resource	Function / Description	Relevance to Benchmarking
High-Performance Computing (HPC) Clusters	GPU/CPU clusters for running MD and AIMD simulations [54]	Essential for performing large-scale simulations across multiple compositions and temperatures.
Ab Initio Molecular Dynamics (AIMD)	DFT-based MD for generating reference data [2] [16]	Provides benchmark-quality data for structural properties and training for MLFFs.
Neural Network Force Fields (e.g., NeuralIL)	ML potentials trained on AIMD data [16]	Used as a high-accuracy benchmark or a next-generation force field for dynamics.
Open Force Field Initiative	Consortium developing open-source force fields [55]	Provides access to modern, rigorously parameterized force fields like OpenFF.
Automated Fitting Procedures	Software for systematic parameter optimization [51]	Enables the development of accurate, system-specific force fields.
Visualization & Analysis Software	Tools for analyzing RDFs, diffusion, etc. (e.g., VMD, MDAnalysis)	Critical for extracting structural and dynamic properties from simulation trajectories.

The systematic benchmarking of force fields is no longer a niche exercise but a fundamental requirement for credible MD simulations, especially in research involving transport properties and dynamic processes. The comparative data presented in this guide clearly demonstrates that the choice of force field significantly impacts quantitative outcomes, sometimes by orders of magnitude [2].

The future of force field development is moving along two complementary paths: the continuous refinement of physics-based empirical potentials and the disruptive adoption of machine-learning approaches. Neural network and other ML potentials show remarkable promise in addressing long-standing pathological deficiencies, offering a path to quantum accuracy in classical simulations [16]. Concurrently, initiatives like the Open Force Field Consortium and new-generation force fields like PHAST 2.0 are bringing greater physical rigor and reproducibility to empirical force field development [55] [52].

For researchers today, the recommended practice is a cautious and evidence-based approach. Before embarking on large-scale production simulations, one should conduct a preliminary benchmarking study for the specific system and properties of interest. This involves comparing the performance of several candidate force fields against available experimental data or AIMD simulations, paying close attention to both structural and dynamic properties. By doing so, the scientific community can progressively close the gap between computational models and reality, enhancing the predictive power of molecular simulation across chemistry, materials science, and drug discovery.

The accuracy of molecular dynamics (MD) simulations in computational chemistry and drug discovery is fundamentally governed by the quality of the force field employed. Force fields are mathematical models that describe the potential energy surface of a molecular system as a function of atomic positions, enabling the calculation of forces that drive atomic motion [56]. Traditional parameterization methods often require extensive manual intervention and thousands of computational iterations, creating significant bottlenecks in research progress [57]. The integration of machine learning (ML) techniques, particularly active learning combined with Gaussian processes (GPs), has emerged as a transformative approach for developing accurate, data-efficient force fields. This guide provides a comprehensive comparison of these advanced parameterization methodologies, benchmarking their performance against conventional alternatives within the specific context of transport properties research.

Active learning represents a paradigm shift from passive data collection to an intelligent, iterative framework where the algorithm itself selects the most informative data points for parameter optimization. When coupled with Gaussian processes—a powerful Bayesian machine learning technique capable of providing principled uncertainty quantification—this approach enables rapid convergence to optimal force field parameters while minimizing computational expense [58]. This combination is particularly valuable for simulating complex molecular systems and their transport properties, where traditional methods struggle with accuracy-transferability trade-offs.

Fundamental Principles

Active learning with Gaussian processes for force field parametrization represents a synergistic combination of two powerful computational frameworks. Gaussian process regression is a Bayesian non-parametric machine learning technique that provides a robust probabilistic approach to regression problems. In the context of force field development, GPs model the potential energy surface by placing a prior over functions and then updating this prior based on quantum mechanical (QM) training data to form a posterior distribution [58]. This methodology naturally provides not only force predictions but also well-calibrated uncertainty estimates for these predictions through the variance of the posterior distribution.

The active learning component operates by strategically leveraging these uncertainty estimates to guide the selection of subsequent training data. Rather than relying on random or exhaustive sampling, the algorithm identifies and queries atomic configurations where the model exhibits highest uncertainty, typically corresponding to regions of chemical space poorly represented in the current training set [57] [58]. This creates a self-improving cycle where each new data point maximizes information gain, leading to dramatically faster convergence compared to traditional approaches.

Key Implementation Variants

Several research groups have developed distinct implementations of this core methodology, each with unique advantages:

• GA-GPR Framework: Yati et al. combined genetic algorithms (GA) with Gaussian process regression (GPR) specifically for sulfone-based electrolytes [57]. In this approach, the genetic algorithm performs a global search of parameter space while GPR guides the selection of promising candidates for evaluation, achieving optimization in just 12 iterations using only 300 data points.

• MGP Acceleration: Vandermause et al. addressed the computational bottleneck of standard GP through their Mapped Gaussian Process (MGP) method, which enables constant-cost evaluation independent of training set size [58]. This is achieved by mapping both forces and uncertainties onto functions of low-dimensional features, making large-scale MD simulations with millions of atoms computationally feasible.

• Memory-Based Dual GPs: Recent work on Memory-Based Dual Gaussian Processes introduces a sophisticated data management strategy that maintains a curated memory of important past examples through Bayesian leverage scoring [59]. This approach is particularly valuable for sequential learning scenarios where access to complete historical data is limited, preventing error accumulation over time.

• ByteFF GNN Parameterization: While not exclusively using GPs, ByteFF employs graph neural networks (GNNs) trained on massive QM datasets (2.4 million optimized molecular fragment geometries with Hessian matrices and 3.2 million torsion profiles) to predict molecular mechanics force field parameters [56]. This represents a complementary data-driven approach to force field development.

Table 1: Comparison of Active Learning and Gaussian Process Methodologies for Force Field Parametrization

Methodology	Key Innovation	Training Data Efficiency	Uncertainty Quantification	Computational Scaling
GA-GPR Framework [57]	Genetic algorithm optimization guided by GPR	300 data points, 12 iterations	Built-in via GPR	Improves with iterations
MGP Acceleration [58]	Mapping of forces/uncertainties to low-dimensional features	Sample-efficient via active learning	Principled Bayesian uncertainty	Constant cost (independent of training size)
Memory-Based Dual GPs [59]	Bayesian leverage scoring for memory management	Effective with limited past data	Dual sparse variational GP	Adapts to data constraints
ByteFF GNN [56]	Graph neural networks on expansive QM datasets	Requires large training data (2.4M geometries)	Not explicitly mentioned	Fast prediction after training

Experimental Protocols and Benchmarking Methodologies

Standardized Evaluation Approaches

Robust benchmarking of force field parameterization methods requires standardized experimental protocols and validation metrics. The most rigorous approaches evaluate performance across multiple dimensions including accuracy, data efficiency, transferability, and computational requirements. For methods targeting transport properties, validation typically focuses on thermodynamic and kinetic properties measurable through MD simulations.

The GA-GPR framework established a comprehensive validation protocol comparing predictions against experimental measurements and reference data for key properties including density, viscosity, diffusion coefficients, and surface tension [57]. Performance was benchmarked against widely used force fields like OPLS, with the GA-GPR model demonstrating superior agreement with experimental values across multiple temperatures and molecular structures.

ByteFF employed a different but equally rigorous approach, validating against quantum mechanical benchmarks including relaxed geometries, torsional energy profiles, and conformational energies/forces [56]. Their evaluation emphasized chemical space coverage, utilizing an expansive dataset derived from the ChEMBL and ZINC20 databases with enhanced diversity through systematic fragmentation and protonation state sampling.

Active Learning Workflows

The active learning workflow for force field parameterization follows a systematic, iterative process that can be visualized as follows:

Diagram 1: Active learning workflow for force field parametrization (AL-FF)

This workflow illustrates the iterative nature of active learning for force field development. The process begins with an initial training set of quantum mechanical data, followed by training of the Gaussian process model. Molecular dynamics simulations are then performed using the current force field, during which configurations with high predictive uncertainty are identified. These uncertain configurations undergo more accurate QM calculations and are added to the training set, after which convergence is evaluated against predefined criteria [57] [58]. This cycle continues until the force field achieves target accuracy across relevant molecular configurations.

Performance Comparison and Benchmarking Data

Quantitative Performance Metrics

Rigorous benchmarking reveals significant performance differences between active learning approaches and traditional parameterization methods. The GA-GPR framework demonstrated exceptional efficiency, achieving optimized parameters for sulfone molecules in just 12 iterations using only 300 data points [57]. This represents a dramatic improvement over previous attempts that required thousands of iterations and parameters. When validated against experimental data, the GA-GPR force field showed excellent agreement for density, viscosity, diffusion coefficients, and surface tension, outperforming the widely used OPLS force field across multiple properties.

The MGP method enabled accelerated Bayesian active learning with performance comparable to classical analytical force fields, achieving simulation speeds several orders of magnitude faster than available neural network or full GP approaches [58]. This performance advantage scales with system size, making MGP particularly suitable for large-scale simulations involving millions of atoms. In application to stanene, the MGP force field successfully captured complex phase transformation behavior at different temperatures, demonstrating transferability across thermodynamic states.

ByteFF achieved state-of-the-art performance on various benchmark datasets, particularly excelling in predicting relaxed geometries, torsional energy profiles, and conformational energies and forces [56]. The method's expansive chemical space coverage, built through training on 2.4 million molecular fragments and 3.2 million torsion profiles, makes it particularly valuable for drug discovery applications where diverse molecular structures must be accurately simulated.

Table 2: Performance Benchmarking of Machine Learning-Optimized Force Fields

Force Field Method	Training Data Size	Key Performance Metrics	Computational Speed	Transport Properties Accuracy
GA-GPR Framework [57]	300 data points, 12 iterations	Excellent agreement with experimental density, viscosity, diffusion coefficients, surface tension	Not specified	Outperformed OPLS force field
MGP Force Fields [58]	Sample-efficient via active learning	Accurate phase transformation prediction in stanene	Million-atom simulations, comparable to classical force fields	Suitable for large-scale dynamics
ByteFF [56]	2.4M geometries, 3.2M torsion profiles	State-of-art for geometries, torsional profiles, conformational energies/forces	Fast prediction after training	Expansive chemical space coverage
Traditional MMFFs [56]	Manual parametrization	Limited by fixed functional forms	High computational efficiency	Varies with system and parametrization

Application to Transport Properties

For research focused specifically on transport properties, the GA-GPR framework has demonstrated particular promise. When applied to sulfone-based electrolytes relevant for energy storage applications, the method accurately captured molecular mobility, caging effects, and interfacial arrangements—all critical factors influencing transport behavior [57]. The optimized force field successfully described both bulk and interfacial properties, enabling more reliable prediction of diffusion coefficients and viscosity across different temperatures and molecular structures.

The transferability of GA-GPR across temperatures and related molecular structures further underscores its value for transport properties research, where behavior under varying thermodynamic conditions is often of primary interest [57]. This robust performance across conditions reduces the need for system-specific reparameterization, accelerating research on molecular systems with potential applications in energy storage, separation processes, and drug delivery.

Technical Implementation and Integration

MGP Acceleration Architecture

The computational acceleration central to the MGP method involves a sophisticated mapping process that can be visualized as follows:

Diagram 2: MGP acceleration architecture for Bayesian force fields

This architecture illustrates how the MGP method achieves its performance advantages. The process begins with full Gaussian process training on quantum mechanical data. Both force predictions and uncertainty estimates are then mapped to low-dimensional features, creating the Mapped Gaussian Process model that enables constant-cost evaluation independent of training set size [58]. This accelerated model supports active learning with rapid uncertainty estimates and ultimately enables production molecular dynamics simulations of systems containing millions of atoms.

The Scientist's Toolkit: Essential Research Reagents and Software

Implementation of these advanced parameterization methods requires specific computational tools and datasets:

Table 3: Essential Research Tools for ML-Optimized Force Field Development

Tool Category	Specific Examples	Function in Workflow	Key Features
QM Reference Data	B3LYP-D3(BJ)/DZVP calculations [56]	Provides training targets for force field optimization	Balance between accuracy and computational cost
Active Learning Frameworks	FLARE [58], Custom GA-GPR [57]	Manages iterative data selection and model updating	Built-in uncertainty quantification and query strategies
MD Simulation Packages	GROMACS [60], LAMMPS [58]	Performs molecular dynamics with optimized parameters	Compatibility with machine learning force fields
Molecular Datasets	ChEMBL [56], ZINC20 [56]	Provides diverse chemical structures for training	Drug-like molecules with expanded chemical space
Acceleration Methods	MGP [58], Memory-Based Dual GPs [59]	Enables large-scale simulations with Bayesian force fields	Constant-cost evaluation and memory management

Active learning combined with Gaussian processes represents a paradigm shift in force field parameterization, offering substantial improvements in accuracy, efficiency, and transferability compared to traditional methods. The GA-GPR framework demonstrates exceptional performance for specific molecular families like sulfone electrolytes, while MGP methods enable accelerated Bayesian active learning suitable for large-scale simulations. ByteFF's graph neural network approach provides complementary advantages through expansive chemical space coverage, particularly valuable for drug discovery applications.

For researchers focused on transport properties, these methodologies offer more reliable prediction of key properties including diffusion coefficients, viscosity, and interfacial behavior. The systematic benchmarking presented in this guide provides a foundation for selecting appropriate parameterization strategies based on specific research requirements, whether prioritizing data efficiency, computational performance, or chemical diversity. As machine learning approaches continue to evolve, their integration with molecular simulation promises to further enhance our ability to accurately model complex molecular systems and their transport behavior.

Overcoming Polarization Limitations with Neural Network Potentials

Accurate prediction of material transport properties and elastic behavior using molecular dynamics simulations has long been hindered by the challenge of modeling long-range interactions. Traditional neural network potentials (NNPs) often rely on local atomic environments defined by cutoff radii, which inherently limits their ability to describe polarization effects and other non-local phenomena critical for property prediction [61]. These limitations become particularly problematic for systems with charged species, biomolecules, and materials where electrostatic interactions persist over long distances [62] [61]. As the field advances toward benchmarking force fields for transport properties research, understanding and overcoming these polarization limitations has become a central focus of development, leading to diverse architectural solutions across the machine learning interatomic potential (ML-IAP) landscape.

The core challenge stems from a fundamental trade-off: while strict locality provides computational efficiency and transferability, it fails to capture physically important interactions that decay slowly with distance [61]. For instance, a positive and negative charge separated by 15 Å in the gas phase exert a force of approximately 1.47 kcal/mol/Å on each other—a significant interaction that would be completely ignored by a naïve 6 Å cutoff scheme [61]. In response, researchers have developed multiple strategic approaches to incorporate long-range physics while maintaining the accuracy and efficiency advantages of ML-IAPs.

Methodological Approaches for Incorporating Long-Range Physics

Explicit Physics-Based Corrections

One prominent strategy involves augmenting short-range neural network potentials with explicit physics-based corrections for long-range electrostatic and dispersion interactions. The AIMNet2 model exemplifies this approach, decomposing the total energy into local, dispersion, and Coulombic components: UTotal = ULocal + UDisp + UCoul [63]. This architecture uses a message-passing network with a 5.0 Ã… cutoff for local interactions while calculating long-range electrostatic and dispersion terms over the entire system or with an extended cutoff (e.g., 15 Ã…) [63].

Similarly, the CombineNet model addresses long-range interactions by incorporating machine learning-based charge equilibration for electrostatics and the Machine-Learning eXchange-hole Dipole Moment (MLXDM) model for dispersion corrections [62]. This hybrid approach achieves excellent performance on quantum chemical benchmarks, with a mean absolute error of 0.59 kcal/mol against CCSD(T)/CBS benchmarks on the DES370K test set [62]. The implementation of Neural Charge Equilibration (NQE) in AIMNet2 provides a sophisticated method for handling partial charge prediction and redistribution, particularly important for ionic and open-shell species [63].

Extended Message-Passing Architectures

An alternative approach scales existing graph neural network (GNN) frameworks by increasing effective cutoff radii through additional message-passing layers. Each message-passing step enables atoms to communicate with increasingly distant neighbors, effectively extending the model's receptive field without explicitly modifying the local cutoff. For example, eSEN-OMol25 models demonstrate how this approach works in practice [61]:

• eSEN-OMol25-sm: 6 Ã… cutoff × 4 layers = 24 Ã… effective cutoff
• eSEN-OMol25-md: 6 Ã… cutoff × 10 layers = 60 Ã… effective cutoff
• eSEN-OMol25-lg: 12 Ã… cutoff × 16 layers = 192 Ã… effective cutoff

However, this approach faces challenges including "oversquashing" (information compression when passing through multiple edges) and "oversmoothing" (node states becoming indistinguishable with repeated aggregation) [61]. Despite these limitations, models like MACE-OFF23 and MACE-OFF24 have demonstrated remarkable performance on condensed-phase properties including peptide dynamics, organic liquid densities, and molecular crystal lattice energies with effective cutoffs of only 9-12 Ã… [61].

Charge-Equivariant Architectures

Recent advances incorporate charge and spin states directly into model architectures, enabling more accurate treatment of polarization effects. The AIMNet2 model implements a multi-task learning approach that predicts atom-centered partial charges during message passing and refines them iteratively using a charge equilibration procedure [63]. This differs from traditional charge equilibration methods that require solving systems of linear equations, instead learning charge redistribution through the network architecture itself.

The OMol25-trained models represent another significant advancement, as they are trained on data spanning diverse charge and spin states, enabling predictions of redox properties and electron affinities despite not explicitly modeling Coulombic interactions [64]. Surprisingly, these models achieve accuracy comparable to or exceeding low-cost density functional theory methods for predicting reduction potentials and electron affinities, particularly for organometallic species [64].

Comparative Performance Benchmarking

Elastic Property Prediction

Systematic benchmarking of universal machine learning interatomic potentials (uMLIPs) for elastic property prediction reveals significant performance variations across architectures. A comprehensive evaluation of four state-of-the-art models on nearly 11,000 elastically stable materials from the Materials Project database provides quantitative insights into their capabilities [65]:

Table 1: Performance Comparison of uMLIPs for Elastic Property Prediction [65]

Model	Overall Accuracy	Computational Efficiency	Key Strengths
SevenNet	Highest accuracy	Moderate	Best overall performance for elastic properties
MACE	High accuracy	Good	Balanced accuracy and efficiency
MatterSim	Good accuracy	Good	Balanced performance for diverse systems
CHGNet	Less effective overall	Moderate	Charge-informed graph neural network

This benchmark highlights that architectural choices significantly impact model performance for mechanical property prediction, with SevenNet achieving the highest accuracy while MACE and MatterSim provide favorable balances between accuracy and computational efficiency [65]. The study establishes that accurately predicting elastic properties requires capturing the second derivatives of the potential energy surface, presenting qualitatively different challenges than predicting energies and forces alone [65].

Electronic Property Prediction

For electronic properties such as reduction potentials and electron affinities, the performance of NNPs exhibits interesting patterns compared to traditional quantum chemical methods:

Table 2: Performance for Charge-Dependent Properties (Mean Absolute Error) [64]

Method	Main-Group Reduction Potential (V)	Organometallic Reduction Potential (V)	Electron Affinity
B97-3c	0.260	0.414	Not reported
GFN2-xTB	0.303	0.733	Not reported
UMA-S	0.261	0.262	Comparable to DFT
eSEN-S	0.505	0.312	Comparable to DFT

Notably, the OMol25-trained UMA Small model demonstrates exceptional performance for organometallic reduction potentials, outperforming both GFN2-xTB and B97-3c methods despite not explicitly considering charge-based physics in its architecture [64]. This surprising result suggests that extensive training on diverse quantum chemical data may enable NNPs to implicitly capture complex electronic effects without explicit physical modeling of long-range interactions.

Experimental Protocols for Benchmarking

Standardized Evaluation Methodologies

Robust benchmarking of neural network potentials requires standardized protocols that assess performance across multiple property domains. For elastic properties, the established methodology involves calculating the full elastic constant tensor for diverse crystal structures and deriving mechanical properties including bulk modulus, shear modulus, Young's modulus, and Poisson's ratio [65]. These predictions are compared against DFT reference data using metrics including mean absolute error and correlation coefficients.

For electronic properties, reduction potential calculations follow a well-defined protocol: geometry optimization of both reduced and oxidized structures using the target NNP, calculation of electronic energy differences, and application of implicit solvation corrections using models such as CPCM-X [64]. Electron affinity calculations follow similar procedures without solvation corrections. These protocols enable direct comparison between NNPs and traditional quantum chemical methods.

Transferability Assessment

Comprehensive benchmarking must evaluate model transferability beyond training distributions. A suite of tests proposed for assessing transferability includes [66]:

• Radial distribution functions for liquid-phase structural properties
• Mean-squared displacements for diffusion behavior
• Computational X-ray photon correlation spectroscopy (XPCS) for density fluctuations at multiple length scales
• Phonon density of states for solid-phase vibrational properties
• Liquid-solid phase transition behavior for thermodynamic properties

These tests reveal that models trained exclusively on liquid configurations often fail to accurately capture solid-phase behavior, underscoring the importance of diverse training data spanning all relevant phases and conditions [66].

Research Reagent Solutions: Computational Tools

Table 3: Essential Computational Tools for NNP Development and Benchmarking

Tool Name	Type	Primary Function	Key Features
DeePMD-kit	Software Package	NNP training/inference	Deep Potential implementation; high efficiency for extended systems
DP-GEN	Workflow Manager	Automated training data generation	Active learning framework for NNP development
OpenMM	MD Engine	Molecular dynamics simulations	GPU acceleration; extensible plugin architecture
AIMNet2	Pretrained Model	General-purpose NNP	14 elements; charged species; open-source code
OMol25	Dataset	Training data	100M+ calculations; diverse charge/spin states

Architectural Diagrams

NNP Approaches for Long-Range Interactions

Force Field Benchmarking Workflow

The field of neural network potentials has made significant strides in overcoming polarization limitations through diverse architectural innovations. The benchmarking studies summarized demonstrate that no single approach universally dominates; rather, the optimal strategy depends on the specific application domain and property targets. For elastic property prediction, models like SevenNet and MACE currently lead in accuracy and efficiency balance [65], while for electronic properties, OMol25-trained models show surprising capability despite architectural simplifications [64].

Future developments will likely focus on integrating the strengths of these approaches—combining explicit physics with sophisticated architectural innovations and expanded training data. As benchmark methodologies become more standardized and comprehensive, the field will benefit from more rigorous comparisons across architectural paradigms, ultimately accelerating the development of universally accurate neural network potentials capable of modeling complex polarization effects across diverse chemical and materials systems.

In computational science, a central strategic dilemma is whether to use a bespoke specialist model, built from scratch for a specific system, or to adapt a generalist foundation model, pre-trained on massive and diverse datasets, for a specialized task [43] [67]. This choice is critical in fields like materials science and drug discovery, where the accuracy of predicting properties like interatomic forces or molecular binding can dictate the success or failure of a research endeavor [43] [68]. Foundation models, which are large-scale machine learning models pre-trained on vast amounts of data, have revolutionized fields like natural language processing and are now making significant inroads into scientific domains [69] [70].

The trade-offs between these approaches are multifaceted, involving data efficiency, computational cost, predictive accuracy for both equilibrium and non-equilibrium properties, and susceptibility to failure on out-of-distribution tasks [43]. This guide provides an objective benchmarking comparison, framed within transport properties and force field research, to help researchers and drug development professionals navigate these complex trade-offs. We synthesize evidence from recent studies that systematically evaluate these models across a range of critical metrics.

Performance Comparison: Specialist vs. Generalist Models

The performance gap between specialist and generalist models can be significant, but it varies greatly depending on the task, the fine-tuning strategy, and the specific property being predicted. The following table summarizes key quantitative findings from recent benchmarking studies.

Table 1: Comparative Performance of Specialist and Generalist Models

Domain / Task	Specialist Model Performance	Generalist Model Performance	Key Findings & Context
Health Assessment via PPG Signals [69]	27% higher win score in full-tuning scenario across 51 tasks.	Lower win score, but adaptable to diverse tasks.	Specialist models demonstrated superior capability in cardiac assessment, lab value estimation, and cross-modal inference.
Kinetic Properties in 2D Materials (Cr-doped Sb₂Te₃) [43]	From-scratch training required for robust performance on non-equilibrium processes.	Zero-shot predictions for kinetic properties (e.g., migration barriers) showed dramatic divergence from reference data.	Targeted fine-tuning of a generalist model substantially outperformed zero-shot approaches but induced catastrophic forgetting of long-range physics.
Data Efficiency (Interatomic Potentials) [71]	Achieved state-of-the-art accuracy with as few as 100-1000 reference calculations.	Required orders of magnitude more training data to achieve similar accuracy.	Specialist models built with equivariant architectures (e.g., NequIP) demonstrated remarkable data efficiency.
Binding Affinity Prediction (Drug Discovery) [68]	Hermes model reported 200-500x faster inference than Boltz-2 with improved predictive performance.	Boltz-2 predicted binding affinity in 20 seconds, a thousand times faster than physics-based simulations.	Specialist models (Hermes) leveraged domain-specific data and simpler architectures for speed and accuracy.

Beyond these quantitative metrics, analysis of the learned representations reveals a fundamental difference: different training paradigms produce distinct, non-overlapping latent space encodings, suggesting they capture different aspects of the underlying physics [43]. This implies that the choice of model type not only affects performance but also the very nature of the physical insights that can be gleaned.

Experimental Protocols for Benchmarking

To ensure fair and reproducible comparisons, benchmarking studies must employ rigorous and standardized experimental protocols. The following methodologies are critical for evaluating model performance in computational materials science and drug discovery.

Migration Pathway Analysis with Nudged Elastic Band (NEB)

This protocol is designed to test a model's interpolation and extrapolation capabilities by probing non-equilibrium kinetic processes, which are more stringent than equilibrium property tests [43].

• System Selection: Choose a technologically relevant system where atomic migration is critical to functionality (e.g., Cr diffusion in the 2D van der Waals material Sbâ‚‚Te₃ for spintronic applications) [43].
• Defect Configuration: Model the system with a specific defect (e.g., a dopant atom) and identify its stable and metastable positions.
• Pathway Generation: Use the Nudged Elastic Band (NEB) method to compute the minimum energy path (MEP) and the energy barrier for migration between stable sites.
• Model Evaluation:
  • Compute the NEB trajectory using the machine-learned force field (MLFF) and a high-fidelity reference method like Density Functional Theory (DFT).
  • Quantify the error in the predicted migration energy barrier.
  • Analyze the divergence in the predicted atomic pathway and the final configurations.

This protocol serves as a powerful physical probe because it simultaneously tests a model's ability to handle both interpolation (near equilibrium sites) and extrapolation (along the high-energy transition path) [43].

Binding Affinity Prediction for Drug Discovery

This protocol benchmarks models on their ability to predict the strength of interaction between a protein and a small molecule, a key task in early-stage drug discovery [68].

• Dataset Curation: Use established experimental binding affinity databases like ChEMBL and BindingDB. To ensure biophysical plausibility, computationally folded protein-ligand structures from repositories like SAIR (Structurally-Augmented IC50 Repository) can be used [68].
• PoseBusters Validation: Run all computationally folded structures through PoseBusters, a tool that evaluates the biophysical plausibility of protein-ligand complexes, to filter out distorted geometries [68].
• Model Training & Testing:
  • For specialist models, train on a curated, high-quality dataset specific to the target protein family or a proprietary in-house dataset [68].
  • For generalist models, use a zero-shot prediction approach or fine-tune on a subset of the target data.
• Performance Metrics: Evaluate models based on the correlation between predicted and experimental binding affinity values (e.g., IC50). Computational speed (inferences per second) is also a critical metric.

Workflow Visualization of Model Benchmarking

The following diagram illustrates the logical workflow and decision points involved in the strategic benchmarking of specialist versus generalist models, as informed by the reviewed experimental protocols.

Diagram 1: Strategic Benchmarking Workflow for Specialist and Generalist Foundation Models

The Scientist's Toolkit: Essential Research Reagents & Solutions

Building and benchmarking high-quality models requires a suite of computational tools and data resources. The table below details key solutions used in the featured experiments and the broader field.

Table 2: Key Research Reagent Solutions for Force Field and Drug Discovery Research

Tool / Resource	Type	Primary Function	Relevance to Specialist/Generalist Models
CHGNet, M3GNet, MACE-MP [43]	Generalist Foundation Model	Pre-trained interatomic potentials for materials.	Serves as a base generalist model for zero-shot prediction or fine-tuning for specific material systems.
Nudged Elastic Band (NEB) [43]	Computational Algorithm	Calculates minimum energy paths and barriers for atomic migration.	Critical diagnostic probe for benchmarking model performance on non-equilibrium, kinetic properties.
PoseBusters [68]	Validation Software	Checks the biophysical plausibility of protein-ligand 3D structures.	Ensures quality of training data for specialist models and validates outputs from generalist models like Boltz-2.
SAIR Repository [68]	Dataset	Open-access repository of computationally folded protein-ligand structures with experimental affinity data.	Provides a large, high-quality dataset for training specialist affinity prediction models or fine-tuning generalists.
e3nn [71]	Software Library	Framework for building E(3)-equivariant neural networks.	Enables the development of highly data-efficient specialist models (e.g., NequIP) for molecular and materials systems.
Boltz-2 [68]	Specialist Model	Predicts protein-ligand binding affinity with high speed.	A benchmark specialist model for binding affinity, demonstrating the potential for high accuracy and efficiency.
Hermes [68]	Specialist Model	Predicts small molecule-protein binding likelihood from sequence and SMILES data.	Exemplifies a compact, fast specialist model that outperforms larger structural models on its specific task.

The debate between specialist and generalist foundation models does not yield a single winner. Evidence shows that specialist models, whether trained from scratch or heavily fine-tuned, consistently deliver superior accuracy and efficiency for well-defined, domain-specific tasks such as cardiac assessment from PPG signals [69] or predicting protein-ligand binding affinity [68]. Their remarkable data efficiency [71] makes them indispensable when high-fidelity data is scarce or computationally expensive to produce.

However, generalist models provide a powerful and flexible starting point. The key strategic insight is that naïve fine-tuning of a generalist model can lead to catastrophic forgetting of its broad knowledge [43]. Therefore, the optimal path forward often lies in hybrid approaches and intelligent benchmarking. Researchers should use rigorous physical probes, like migration pathways, to diagnose model failures and guide active learning [43]. The choice is not merely a technical one but a strategic decision that influences not only predictive accuracy but also the physical interpretability and robustness of the resulting model.

Improving Prediction of Kinetic Barriers and Rare Events

Accurately predicting kinetic barriers and rare events is a fundamental challenge in molecular simulation, with significant implications for materials science and drug development. The reliability of these simulations is intrinsically linked to the quality of the empirical force fields used to describe atomic interactions. Force fields are mathematical representations of the potential energy of a system of particles, and their parameters are typically fitted to reproduce selected experimental measurements or ab initio calculations [2]. When a force field inaccurately represents the true energy landscape of a system, it leads to erroneous predictions of key properties, including the heights of kinetic barriers and the rates of rare, activated processes. These processes, while infrequent, are crucial for understanding phenomena like protein folding, ligand unbinding, and chemical reactions [72]. This guide provides a comparative analysis of force field performance, offering researchers a framework for selecting and validating force fields for studies of kinetics and transport properties.

Force Field Benchmarking: Key Concepts and Properties

Benchmarking a force field involves systematically comparing its predictions against reliable reference data, which can come from high-level ab initio molecular dynamics (AIMD) simulations or experimental measurements. The benchmarking process typically assesses two classes of properties:

• Structural Properties: These are equilibrium properties that define the geometry of the system. Key metrics include:
  • Density: A fundamental thermodynamic property.
  • Bond Lengths and Coordination Numbers: Describe the local atomic environments and bonding [2].
• Dynamic and Transport Properties: These describe the time-evolving behavior and movement within the system. They are more challenging to predict accurately and are highly sensitive to force field quality. Key metrics include:
  • Self-diffusion Coefficients: Measure the rate at which a particle diffuses in a system.
  • Electrical Conductivity: Relevant for ionic systems.
  • Viscosity: Resistance to flow [73].
  • Rates of Rare Events: The frequency of barrier-crossing events, which can be inferred from free energy barriers [74].

A force field may perform well for structural properties but poorly for dynamics, underscoring the need for comprehensive benchmarking. For instance, in molten oxides, some force fields accurately reproduce densities but fail to capture diffusion dynamics [2]. Similarly, for intrinsically disordered proteins (IDPs), force fields developed for structured proteins can generate overly compact or extended conformations, misrepresenting the true conformational ensemble [75].

Comparative Analysis of Force Field Performance

The performance of a force field must be evaluated in the context of a specific material or molecular system. The following case studies highlight how benchmarking reveals critical differences between popular force fields.

Case Study 1: Oxide Melts (CaO-Al(2)O(3)-SiO(_2))

A systematic benchmarking of three force fields—Matsui, Guillot, and Bouhadja—for CaO-Al(2)O(3)-SiO(_2) melts provides a clear example of performance variation [2]. This ternary system is critical in industrial processes like steelmaking and glass manufacturing.

Table 1: Benchmarking Force Fields for Oxide Melts (CaO-Al(_2)O(_3)-SiO(_2))

Force Field	Structural Properties	Transport Properties	Overall Assessment
Matsui	Accurately reproduces densities and Si–O tetrahedral environments.	Less accurate for dynamics and conductivity.	Good for structure, poor for transport.
Guillot	Accurately reproduces densities and Si–O tetrahedral environments.	Less accurate for dynamics and conductivity.	Good for structure, poor for transport.
Bouhadja	Better agreement with AIMD for Al–O and Ca–O bonding.	Best agreement with experimental activation energies and conductivity trends.	Most accurate and reliable for transport phenomena.

The study concluded that while the Matsui and Guillot force fields were accurate for structural properties, the Bouhadja force field was superior for predicting dynamic and transport properties, demonstrating better transferability across compositions and temperatures not included in its original parameterization [2].

Case Study 2: Intrinsically Disordered Proteins (R2-FUS-LC Region)

The challenge of force field selection is also apparent in biological systems. A study benchmarking 13 force fields for the intrinsically disordered R2-FUS-LC region, implicated in ALS, evaluated performance based on the compactness (radius of gyration), secondary structure propensity, and intra-peptide contact maps [75].

Table 2: Top-Tier Force Fields for an Intrinsically Disordered Protein (R2-FUS-LC)

Force Field	Water Model	Key Strengths	Performance Summary
CHARMM36m2021	mTIP3P	Most balanced FF, generates various conformations compatible with experiments, computationally efficient.	Top-ranked; best overall score.
CHARMM36m	TIP3P	Good performance, tends to generate more extended conformations.	Middle-ranking group.
AMBER a99SB-4p	TIP4P-Ew	Good performance, but tends to generate more compact conformations with more non-native contacts.	Middle-ranking group.
AMBER a19SB	OPC	Good performance across measures.	Middle-ranking group.

The study revealed that AMBER force fields generally produced more compact conformations with more non-native contacts compared to CHARMM force fields. The top-ranking CHARMM36m2021 force field with the mTIP3P water model was identified as the most balanced and accurate for this specific IDP [75].

Methodologies for Benchmarking and Kinetic Studies

Adhering to rigorous protocols is essential for obtaining reliable and reproducible results when computing transport properties and studying rare events.

Best Practices for Equilibrium Molecular Dynamics (EMD)

For predicting properties like self-diffusivity and viscosity from EMD simulations, key best practices include [73]:

• System Size and Simulation Time: Ensuring the simulation cell is large enough and the simulation is long enough to avoid finite-size effects and ensure proper statistical sampling.
• Trajectory Analysis: Using multiple, independent trajectories to improve statistics and validate results.
• Force Field Validation: Comparing simulation output against experimental data to test the adequacy of the force field model itself.

Enhanced Sampling Techniques for Rare Events

Standard MD simulations cannot adequately sample rare events due to the infrequency of barrier crossing. Enhanced sampling methods are therefore required:

• Temperature Accelerated Sliced Sampling (TASS): This method facilitates exhaustive exploration of high-dimensional collective variable (CV) space using a combination of umbrella biases, metadynamics biases, and temperature acceleration of CVs. A recent advancement allows for the calculation of rate constants from TASS simulations by leveraging artificial neural networks to represent free energy landscapes [74].
• Forward-Flux Sampling (FFS): This technique uses a series of non-intersecting interfaces between initial and final states to compute rate constants and generate transition paths without requiring a priori knowledge of the reaction coordinate [72].
• Infrequent Metadynamics (IMetaD): A method to obtain kinetic information from biased simulations, which was integrated with the TASS approach to recover rate constants [74].

The workflow below illustrates a generalized protocol for benchmarking force fields and studying rare events, integrating the methodologies discussed.

Diagram 1: A generalized workflow for force field benchmarking and rare event simulation.

Essential Tools and Reagent Solutions

Successful simulation studies rely on a suite of software tools and well-parameterized force fields, which function as the "research reagents" of computational science.

Table 3: Key Research Reagent Solutions for Molecular Simulation

Tool / Reagent	Type	Primary Function	Relevance to Kinetics & Rare Events
LAMMPS	Software	General-purpose molecular dynamics simulator.	High-performance MD for solids, soft materials; supports various enhanced sampling methods.
GROMACS	Software	High-performance MD package, mainly for biomolecules.	Efficient EMD for computing transport properties like diffusivity and viscosity.
AMBER	Software & Force Field	Suite for biomolecular simulations, includes force fields.	Includes force fields like a99SB-4p and a19SB, used for benchmarking IDPs and protein kinetics.
CHARMM	Software & Force Field	Suite for biomolecular simulations, includes force fields.	Includes force fields like CHARMM36m, critical for accurate IDP and protein folding studies.
OpenMM	Software	High-performance, scriptable MD library.	Highly flexible platform for implementing custom enhanced sampling protocols.
PLUMED	Library	Plugin for free energy calculations in MD.	Provides extensive enhanced sampling methods, including metadynamics, essential for rare events.
Bouhadja FF	Force Field	Empirical force field for oxide melts.	Identified as superior for transport properties in CaO-Al(2)O(3)-SiO(_2) melts [2].
CHARMM36m2021	Force Field	Modified CHARMM force field for IDPs.	Top-performing force field for the disordered R2-FUS-LC region [75].

The accurate prediction of kinetic barriers and rare events is contingent upon the careful selection and rigorous benchmarking of force fields. As demonstrated, force field performance is highly system-dependent; a force field that excels for oxide melts may not be applicable to proteins, and even within a class of molecules, significant variations exist. The consistent best practice is to conduct a preliminary benchmarking study against reliable experimental or ab initio data for both structural and dynamic properties relevant to the system of interest. By leveraging comparative guides, standardized protocols for computing transport properties, and robust enhanced sampling techniques, researchers can make informed choices that significantly improve the predictive power of their molecular simulations in drug development and materials design.

Validation Protocols and Comparative Analysis of Force Field Accuracy

The accuracy of molecular dynamics (MD) simulations is fundamentally constrained by the quality of the force fields that govern atomic interactions. As computational methods play an increasingly pivotal role in materials science and drug discovery, establishing robust validation benchmarks against experimental data and high-level ab initio molecular dynamics (AIMD) has become essential. Traditional force fields, based on molecular mechanics (MM) with limited functional forms, face significant challenges in representing the expansive chemical space relevant to drug-like molecules. Meanwhile, machine learning force fields (MLFFs) have emerged as powerful tools that bridge the accuracy-efficiency gap, offering near-ab initio accuracy with computational speeds approaching classical methods. However, the predictive power of both traditional and MLFFs hinges on comprehensive validation protocols that evaluate performance across diverse chemical environments and physical properties. This guide systematically compares current force field validation methodologies, providing researchers with a framework for assessing performance against experimental and AIMD benchmarks across multiple domains.

Force Field Validation Frameworks and Methodologies

Multi-Source Data Integration Strategies

Modern force field development employs integrated validation strategies that leverage both computational and experimental data sources. The fused data learning approach simultaneously utilizes Density Functional Theory (DFT) calculations and experimental measurements during training, creating models with higher overall accuracy compared to those trained on a single data source. This methodology alternates between a DFT trainer, which performs standard regression on quantum chemical data (energies, forces, virial stress), and an EXP trainer, which optimizes parameters to match experimental observables through differentiable trajectory reweighting techniques. This hybrid strategy corrects known DFT functional inaccuracies while maintaining transferability to out-of-target properties.

For machine-learned force fields, fine-tuning has emerged as a critical technique for achieving quantitative accuracy in specialized applications. This process adapts pre-trained foundation models using system-specific training data, dramatically improving model accuracy across diverse architectures. Benchmarking across five leading MLFF frameworks (MACE, GRACE, SevenNet, MatterSim, and ORB) reveals that fine-tuning typically reduces force errors by 5-15× and improves energy accuracy by 2-4 orders of magnitude, enabling quantitatively accurate predictions of system-specific physical properties that foundation models fail to capture.

Hierarchical Validation Protocols

A hierarchical validation strategy encompassing multiple scales and physical domains ensures robustness in force field parameterization. This approach validates accuracy across three critical domains: (1) bulk phase properties, where MLFF predictions of energy fluctuations and structural parameters are compared against AIMD benchmarks; (2) interfacial reactivity, where energy profiles, bond lengths, and charge variations at material interfaces are evaluated; and (3) chemical decomposition properties, where the force field's ability to capture bond-breaking and forming events is assessed. This multi-scale validation provides comprehensive assessment before deploying force fields to large-scale production simulations.

Table 1: Key Methodologies in Force Field Validation

Validation Approach	Data Sources	Key Techniques	Primary Applications
Fused Data Learning	DFT + Experimental data	Differentiable Trajectory Reweighting (DiffTRe), Alternating optimization	Correcting DFT inaccuracies, Improving experimental agreement
Fine-Tuning	System-specific AIMD trajectories	Transfer learning, Active learning	Specialized applications, Architecture-agnostic accuracy improvement
Hierarchical Validation	Bulk, interface, and reaction properties	Multi-scale benchmarking, AIMD comparison	Battery interfaces, Reactive systems, Complex materials
Cross-Validation	Diverse molecule benchmark sets	k-fold validation, Leave-one-out testing	Drug-like molecules, Chemical space coverage

Quantitative Benchmarking: Performance Comparison Across Force Field Types

Accuracy Metrics and Performance Indicators

Force field validation employs multiple quantitative metrics to assess performance across different physical properties. For MLFFs trained on DFT data, standard regression errors including energy errors (typically targeting <43 meV for chemical accuracy), force errors (meV/Ã…), and virial stress errors provide fundamental accuracy measures. When validating against experimental data, key benchmarks include mechanical properties (elastic constants), structural parameters (lattice constants, radial distribution functions), thermodynamic properties (free energies, enthalpies of vaporization, heat capacities), and dynamic properties (diffusion coefficients, viscosities). For drug discovery applications, accurate prediction of solvation free energies, partition coefficients, and conformational energies is particularly critical.

The transferability of force fields across different system sizes and chemical environments represents another crucial validation metric. Studies demonstrate that MLFFs trained on small systems (~60 atoms) can maintain accuracy when scaled to medium-sized systems (~480 atoms), but often exhibit pathological failures including bond breaking and unphysical atomic overlaps when applied to significantly larger systems (~1500 atoms). This underscores the importance of validating force fields at the scale of intended application, particularly for complex interfacial systems.

Comparative Performance Across Force Field Architectures

Recent systematic evaluations reveal significant performance differences across force field architectures and training methodologies. Traditional MM force fields parameterized using graph neural networks (GNNs), such as ByteFF, demonstrate state-of-the-art performance in predicting relaxed geometries, torsional energy profiles, and conformational energies across expansive chemical spaces. Meanwhile, MLFFs show remarkable accuracy in reproducing AIMD-derived properties while achieving computational speedups of several orders of magnitude.

Table 2: Performance Comparison of Force Field Validation Approaches

Force Field Type	Training Data	Energy Error	Force Error	Experimental Agreement	Transferability
Traditional MM (ByteFF)	2.4M QM geometries, 3.2M torsion profiles	Accurate for conformations	N/A	Good for solvation free energies	Excellent across chemical space
MLFF (Foundation Models)	Materials Project, Alexandria databases	Variable	Architecture-dependent	Limited for specific properties	Broad but quantitatively limited
MLFF (Fine-Tuned)	System-specific AIMD	2-4 orders improvement	5-15× improvement	Excellent for target properties	High for trained systems
Fused Data MLFF	DFT + Experimental	Slight increase from DFT-only	Slight increase from DFT-only	Best overall agreement	Maintained for out-of-target properties

For materials systems, MLFFs trained exclusively on DFT data often fail to quantitatively reproduce experimental lattice parameters and elastic constants, reflecting inaccuracies in the underlying DFT functionals. The fused data learning approach successfully corrects these discrepancies while maintaining accuracy for other properties. For instance, in titanium systems, fused data MLFFs simultaneously reproduce experimental temperature-dependent elastic constants and lattice parameters while maintaining DFT-level accuracy for energies and forces.

Experimental Protocols for Force Field Validation

Benchmarking Against AIMD Data

Validation against AIMD calculations provides atomic-level accuracy assessment without experimental uncertainties. The standard protocol involves:

• System Preparation: Constructing charge-neutral interface models through careful slab preparation and water box equilibration using packages like PACKMOL. Slab thickness is determined through convergence tests of band alignment and water adsorption energies [76].

• AIMD Production Runs: Performing 20-30 ps AIMD simulations using mixed Gaussian and plane-wave basis set codes (e.g., CP2K/QUICKSTEP) with PBE functionals, Grimme D3 dispersion correction, and GTH pseudopotentials. Simulations typically employ an NVT ensemble with a 0.5 fs timestep at 330K to avoid glassy behavior of PBE water [76].

• MLFF Training: Extracting 50-100 evenly distributed structures from AIMD trajectories as initial training datasets. Using active learning workflows (e.g., DP-GEN, ai2-kit) for iterative expansion through training, exploration, screening, and labeling cycles until >99% of sampled structures achieve low uncertainty [76].

• Property Comparison: Evaluating energy fluctuations, structural parameters (bond lengths, angles), radial distribution functions, and dynamical properties between AIMD and MLFF trajectories using specialized toolkits (e.g., ECToolkits, MDAnalysis) [76].

This approach was successfully applied to validate an on-the-fly MLFF for lithium metal battery interfaces, where minimal discrepancies in energy profiles, FSI− bond lengths, and net charge variations were observed between AIMD and MLFF simulations [77].

Validation Against Experimental Measurements

Experimental validation requires comparing simulation-derived properties with measured values:

• Structural Validation: Comparing calculated crystal structures with X-ray crystallography data for bond lengths, angles, and torsions. Assessing radial distribution functions against neutron scattering data for liquid systems [78].

• Spectroscopic Validation: Computing vibrational frequencies from MD simulations and comparing with infrared and Raman spectroscopic measurements. Evaluating phonon density of states against inelastic scattering data [78] [21].

• Thermodynamic Validation: Calculating solvation free energies using alchemical free energy methods (e.g., exponential reweighting) and comparing with experimental hydration free energy databases (e.g., FreeSolv). Assessing enthalpies of vaporization, heat capacities, and phase transition temperatures [78] [79].

• Mechanical Property Validation: Computing elastic constants from stress-strain relationships and comparing with experimental measurements across temperature ranges. Evaluating lattice parameters against temperature-dependent X-ray diffraction data [21].

• Dynamic Property Validation: Calculating diffusion coefficients from mean-square displacement analysis and comparing with pulsed-field gradient NMR or tracer measurements. Determining viscosity from stress autocorrelation functions [80].

The following workflow diagram illustrates the integrated validation process combining both AIMD and experimental benchmarking:

Research Reagent Solutions: Essential Tools for Force Field Validation

Table 3: Essential Computational Tools for Force Field Validation

Tool Name	Type	Primary Function	Application in Validation
CP2K/QUICKSTEP	AIMD Software	Ab initio molecular dynamics	Generating reference data for MLFF training
DeePMD-kit	MLFF Framework	Training neural network potentials	Developing MLFFs from AIMD data
LAMMPS	MD Simulator	Molecular dynamics simulations	Running production MLMD simulations
DP-GEN	Active Learning	Automated training data generation	Iterative MLFF improvement
ECToolkits	Analysis Tool	Analyzing electrochemical properties	Water density profiles, interface structure
MDAnalysis	Analysis Tool	Trajectory analysis	Processing MD simulation data
aMACEing Toolkit	Fine-Tuning	Unified MLIP fine-tuning	Cross-architecture model optimization
DiffTRe	Differentiable MD	Gradient-based parameter optimization	Training on experimental data

The establishment of comprehensive validation benchmarks against experimental and AIMD data represents a critical advancement in force field development. Integrated approaches that combine quantum chemical data with experimental measurements through fused learning strategies demonstrate superior accuracy compared to single-source training. Meanwhile, fine-tuning methodologies enable researchers to adapt foundation models to specific systems with minimal computational overhead. As force field complexity increases with the adoption of machine learning approaches, standardized validation protocols encompassing structural, thermodynamic, and dynamic properties across multiple scales will become increasingly important. The benchmarking methodologies and comparative analyses presented in this guide provide researchers with a framework for rigorous force field evaluation, ultimately enhancing the reliability of molecular simulations in materials design and drug discovery.

Molecular dynamics (MD) simulations have become an indispensable tool in computational chemistry, materials science, and drug discovery, providing atomistic insights into structural and dynamic properties of biological and material systems. The accuracy of these simulations critically depends on the force fields—empirical mathematical functions and parameter sets that describe the potential energy of a system of particles. Despite decades of development, no universal force field exists that performs optimally across all chemical systems and properties, creating a critical need for systematic benchmarking to guide force field selection for specific applications.

This review addresses the pressing need for evidence-based guidance in force field selection by presenting a structured comparative analysis across diverse molecular systems. We focus particularly on performance in predicting transport properties—essential for understanding diffusion, conductivity, and permeability in various applications—where force field accuracy remains particularly challenging. Through carefully selected case studies spanning oxide melts, polymeric membranes, and intrinsically disordered proteins, we provide researchers with a framework for evaluating force field performance against experimental data and high-level theoretical calculations.

Methodological Framework for Force Field Benchmarking

General Benchmarking Workflow

The evaluation of force fields follows a systematic workflow that begins with the selection of appropriate model systems and reference data. The following diagram illustrates the general benchmarking approach applied across our case studies:

Figure 1: Generalized workflow for force field benchmarking studies. The process begins with defining the system and target properties, proceeds through simulation and comparison with reference data, and concludes with performance analysis and specific recommendations.

Key Performance Metrics

Across benchmarking studies, force fields are typically evaluated against several categories of properties:

• Structural properties: Density, radial distribution functions, coordination numbers
• Dynamic properties: Diffusion coefficients, viscosity, electrical conductivity
• Thermodynamic properties: Free energies, lattice energies, solvation free energies
• Mechanical properties: Young's modulus, elastic constants

Case Study I: Oxide Melts for Industrial Applications

The CaO-Al₂O₃-SiO₂ ternary oxide system is of significant industrial relevance, particularly in its molten state for processes like steelmaking and glass manufacturing [2]. This system presents particular challenges for force field development due to its mixed ionic-covalent bonding characteristics and the high temperatures (1400-1600°C) relevant to industrial conditions.

In this benchmarking study, three empirical force fields were evaluated across ten compositions and five temperatures [2]:

• Matsui et al. (Born-Mayer-Huggins potential)
• Guillot and Sator (Buckingham potential)
• Bouhadja et al. (Born-Mayer-Huggins potential)

Simulations were performed using classical molecular dynamics with systems containing thousands of atoms. Structural properties (density, bond lengths, coordination numbers) were validated against experimental data and CALPHAD models, while dynamic properties (self-diffusion coefficients, electrical conductivity) were compared with experimental measurements and ab initio MD (AIMD) calculations [2].

Performance Comparison and Recommendations

Table 1: Performance comparison of force fields for CaO-Al₂O₃-SiO₂ oxide melts [2]

Force Field	Structural Properties	Transport Properties	Transferability	Best Use Cases
Bouhadja et al.	Accurate for Al-O and Ca-O bonding; good density prediction	Best agreement with experimental activation energies; accurately captures conductivity trends	Excellent beyond original parameterization	Studies requiring accurate dynamics and transport properties
Matsui et al.	Accurate densities and Si-O tetrahedral environments	Less accurate for diffusion and conductivity	Limited to specific compositions	Structural studies focused on silicate networks
Guillot and Sator	Good structural prediction for certain compositions	Moderate accuracy for transport properties	Moderate	General structural screening

The systematic benchmarking revealed that while Matsui's and Guillot's force fields accurately reproduced densities and Si-O tetrahedral environments, Bouhadja's force field showed superior performance for dynamic properties, demonstrating the best agreement with experimental activation energies and robust transferability beyond its original parameterization range [2]. This study highlights that force fields optimized for structural properties may not necessarily provide accurate predictions for transport properties, emphasizing the need for targeted benchmarking.

Case Study II: Polyamide Reverse Osmosis Membranes

Polyamide (PA) membranes are crucial for water purification and desalination technologies, with performance dictated by sub-nanometer transport phenomena. This study evaluated eleven force field-water combinations for simulating cross-linked polyamide membranes formed by trimesoyl chloride and m-phenylenediamine [46].

The benchmarking protocol included:

• Equilibrium MD simulations of dry and hydrated membranes
• Non-equilibrium MD simulations of reverse osmosis at ultra-high pressures (0.3-1.5 kbar)
• Comparison with experimentally synthesized polyamide membranes with similar chemical compositions
• Evaluation of structural properties (density, porosity, pore size, Young's modulus) and transport properties (water permeability)

Performance Comparison and Recommendations

Table 2: Performance comparison of force fields for polyamide membranes [46]

Force Field	Dry State Properties	Hydrated State Properties	Water Permeability	Computational Efficiency
CVFF	Accurate Young's modulus	Good agreement with experimental hydration	Best performance at experimental pressures	Moderate
SwissParam	Good density prediction	Reasonable hydration behavior	Good agreement with experiment	High
CGenFF	Accurate structural prediction	Moderate hydration behavior	Acceptable permeability prediction	Moderate
GAFF	Variable performance	Underestimation of hydration	Overestimation of permeability	High
PCFF	Systematic overestimation of density	Poor agreement with experimental hydration	Poor performance	Low
DREIDING	Least accurate	Least accurate	Least accurate	High

The study revealed that CVFF, SwissParam, and CGenFF force fields provided the most accurate predictions for both structural properties and water permeability, with CVFF showing particular accuracy in predicting pure water permeability within experimental confidence intervals [46]. Interestingly, the best-performing forcefields predicted the experimental pure water permeability of 3D printed polyamide membranes within a 95% confidence interval, demonstrating the potential for predictive simulation in membrane design.

Case Study III: Intrinsically Disordered Proteins

Intrinsically disordered proteins (IDPs) like the R2 region of the FUS-LC domain challenge traditional force fields parameterized for structured proteins. This study assessed thirteen force fields by simulating the R2-FUS-LC region, an IDP implicated in Amyotrophic Lateral Sclerosis (ALS) [75].

The evaluation methodology included:

• Six independent MD simulations of 500 ns each per force field (totaling 3 μs per FF)
• Assessment using three complementary metrics:
  • Radius of gyration (Rg) measuring global compactness
  • Secondary structure propensity (SSP)
  • Intra-peptide contact maps
• Comparison with experimental NMR and cryo-EM structures

Performance Comparison and Recommendations

Table 3: Performance comparison of force fields for the R2-FUS-LC intrinsically disordered protein [75]

Force Field	Compactness (Rg) Score	Contact Map Score	Secondary Structure Score	Overall Ranking
c36m2021s3p	0.74	0.76	0.67	Top
a99sb4pew	0.72	0.70	0.65	Top
a19sbopc	0.71	0.69	0.63	Top
c36ms3p	0.70	0.65	0.61	Top
a99sbdisp	0.55	0.62	0.59	Middle
a99sbCufix3p	0.52	0.58	0.57	Middle
c36m3pm	0.45	0.81	0.42	Middle
c22s3p	0.48	0.55	0.51	Middle
c27s3p	0.25	0.30	0.28	Bottom
a03ws	0.22	0.28	0.25	Bottom
a14sb3p	0.29	0.61	0.60	Bottom

The comprehensive evaluation revealed that CHARMM36m2021 with mTIP3P water model (c36m2021s3p) emerged as the most balanced force field, capable of generating diverse conformations compatible with experimental structures [75]. The study also highlighted systematic tendencies: AMBER force fields generally produced more compact conformations with more non-native contacts compared to CHARMM force fields. Notably, the best-performing force fields demonstrated computational advantages, with mTIP3P water model being more efficient than four-site water models used in top-ranked AMBER force fields.

Table 4: Essential research reagents and computational resources for force field benchmarking

Resource Category	Specific Tools	Function and Application
Simulation Software	TINKER, OpenMM, GROMACS, AMBER, CHARMM, NAMD, Materials Studio	Molecular dynamics engines for running simulations with various force fields [81] [46] [82]
Force Field Families	AMBER, CHARMM, OPLS-AA, GROMOS, COMPASS, GAFF, CGenFF	Parametrized potential functions for different molecular systems [46] [75] [83]
Water Models	TIP3P, TIP4P, SPC, SPC/ε, mTIP3P	Solvent models with different balance of accuracy and efficiency [46] [84] [75]
Quantum Chemistry Codes	Density Functional Theory (DFT) packages	Generating reference data for force field parameterization and validation [2] [85]
Analysis Tools	VMD, MDAnalysis, in-house scripts	Extracting structural and dynamic properties from simulation trajectories [2] [46] [75]
Benchmark Datasets	Cambridge Structural Database, Gen2-Opt, DES370K, TorsionNet-500	Curated experimental and theoretical data for force field validation [86] [83]

Cross-Cutting Insights and Recommendations

Unified Force Field Evaluation Workflow

Based on the case studies, we can synthesize a unified approach for force field evaluation specific to transport properties research:

Figure 2: Specialized workflow for evaluating force fields for transport properties research. The process emphasizes validation of both structural and dynamic properties before proceeding to production simulations.

Field-Specific Recommendations

Based on our comparative analysis, we provide the following field-specific recommendations:

• For oxide melts and inorganic systems: Bouhadja's force field demonstrates superior performance for transport properties, while Matsui's potential remains suitable for structural studies [2].

• For polymer membranes and materials design: CVFF and SwissParam provide the best balance of accuracy for structural and transport properties, though careful validation against system-specific experimental data remains essential [46].

• For intrinsically disordered proteins: CHARMM36m2021 with mTIP3P water model currently provides the most balanced performance, with advantages in computational efficiency compared to alternatives [75].

• For molecular crystals: COMPASSIII outperforms other force fields for lattice energy and density predictions, though careful attention to parameterization for specific functional groups (e.g., nitroaromatics) is recommended [83].

Emerging Trends and Future Directions

The field of force field development and validation is rapidly evolving, with several promising directions emerging:

• Polarizable force fields: Models like AMOEBA represent the next generation of force fields, incorporating many-body effects through atomic multipoles and explicit polarization, showing particular promise for protein-ligand binding and computational crystallography [81].

• Machine learning potentials: Hybrid approaches like ResFF (Residual Learning Force Field) integrate physics-based terms with neural network corrections, demonstrating improved accuracy for torsional profiles and intermolecular interactions while maintaining physical interpretability [86].

• Information-theoretic validation: New analysis methods using Shannon entropy, Fisher information, and complexity measures provide sophisticated tools for quantifying force field performance against electronic structure benchmarks [84].

• Automated parameter optimization: Platforms like Pipeline Pilot enable high-throughput force field validation and parameter refinement across diverse chemical spaces, accelerating the development of more accurate and transferable potentials [83].

As these advanced methodologies mature, we anticipate increasingly robust and predictive force fields that will expand the frontiers of molecular simulation across chemistry, materials science, and drug discovery.

Quantifying Errors in Diffusion Barriers and Electroosmotic Flow

Accurate prediction of transport properties, such as ionic diffusion and electroosmotic flow (EOF), is fundamental to advancements in materials science, microfluidics, and drug development. These phenomena are critical in applications ranging from lithium-ion batteries and integrated circuits to lab-on-a-chip diagnostic devices. However, quantifying and minimizing errors in their simulation remains a significant challenge. This guide provides a comparative analysis of methodologies for benchmarking computational force fields against experimental data, focusing on their accuracy in predicting diffusion barriers and electroosmotic flow dynamics. By objectively presenting performance data and detailed protocols, this review serves as a reference for researchers in selecting and validating computational and experimental approaches.

Benchmarking Force Fields for Diffusion and Transport Properties

The accuracy of classical molecular dynamics (MD) simulations hinges on the empirical force fields describing interatomic interactions. Several force fields have been developed for oxide and polymer systems, each with distinct strengths and weaknesses in predicting structural and transport properties.

Comparative Performance of Force Fields for Oxide Melts

A systematic benchmarking study evaluated three widely used force fields—Matsui, Guillot, and Bouhadja—for simulating CaO-Al₂O₃-SiO₂ melts, a system crucial for industrial processes like steelmaking and glass manufacturing [2]. The study assessed their performance against experimental data and ab initio MD (AIMD) simulations across ten compositions and temperatures from 1400 to 1600 °C.

Table 1: Benchmarking Force Fields for Structural Properties of CaO-Al₂O₃-SiO₂ Melts

Force Field	Density Predictions	Si–O Tetrahedral Environment	Al–O and Ca–O Bonding	Remarks
Matsui	Accurate	Accurately reproduced	Less accurate	BMH potential; good for structure [2]
Guillot	Accurate	Accurately reproduced	Less accurate	Buckingham potential; good for structure [2]
Bouhadja	Slightly less accurate	Slightly less accurate	Best agreement with AIMD	BMH potential; superior for bonding & dynamics [2]

Regarding dynamic transport properties, the study found even more significant discrepancies. Bouhadja's force field demonstrated the best overall agreement with experimental activation energies for diffusion [2]. The predictions for self-diffusion coefficients from different force fields could vary by an order of magnitude or more for similar compositions, underscoring the critical impact of force field selection [2].

Force Fields for Polymer Electrolytes

In energy storage research, MD simulations with Class 1 force fields are used to screen polymer electrolytes for lithium-ion batteries. Benchmarking efforts focus on predicting key transport properties like lithium-ion diffusivities and conductivities. However, their accuracy is often limited by the ability to correctly model the polymer's glass-transition temperature (T𝑔), which significantly influences ion transport dynamics [30]. The convergence of these transport properties must be carefully evaluated as a function of simulation length to ensure reliability, highlighting a key source of potential error in high-throughput screening settings [30].

Experimental Benchmarking of Diffusion Barriers

Experimental quantification of diffusion barriers provides the critical ground-truth data for validating computational models. High-entropy alloy nitride (HEA-N) films have emerged as high-performance diffusion barriers in microelectronics.

Quantitative Performance of HEA-N Barriers

Secondary Ion Mass Spectrometry (SIMS) has been used to quantitatively measure iron diffusion rates in AlCrTaTiZrN HEA-N films deposited on steel [87]. This study provided a precise diffusion coefficient of (7 \times 10^{-22} \text{m}^2\text{s}^{-1} ) at 700 °C, which is 30 times lower than that of conventional polycrystalline titanium nitride (TiN) barriers [87]. The high-entropy alloy barrier also exhibited an activation energy of 2.17 eV, quantitatively confirming its higher diffusion resistance [87].

Table 2: Experimental Diffusion Barrier Performance of HEA-N Films

Barrier Material	Substrate	Diffusing Species	Temperature	Diffusion Coefficient (m²/s)	Key Finding
AlCrTaTiZrN (HEA-N)	Steel	Iron (Fe)	700 °C	(7 \times 10^{-22}) [87]	30x better than TiN [87]
AlCrTaTiZr /AlCrTaTiZr-N	Silicon (Si)	Copper (Cu)	900 °C	Effectively blocks diffusion [88]	Prevents Cu-Si intermetallic formation [88]

Other studies on Cu/AlCrTaTiZr/AlCrTaTiZr-N/Si film stacks have shown that the HEA/HEAN bilayer structure can prevent copper diffusion even after annealing at 900 °C for one hour, as confirmed by transmission electron microscopy (TEM) and atomic probe tomography (APT) [88]. The excellent performance is attributed to the amorphous structure of the metallic HEA layer and the lattice mismatch between the HEA and HEA-N layers, which increases the diffusion path length for copper atoms [88].

Quantification and Control of Electroosmotic Flow

Electroosmotic flow (EOF) is a dominant fluid transport mechanism in microfluidic devices. Its accurate characterization and control are essential for applications like capillary electrophoresis and lab-on-a-chip diagnostics.

Measuring EOF Velocity

Microparticle Image Velocimetry (MPIV) is a key experimental technique for quantifying EOF velocity profiles. In a square 200×200 μm polydimethyl siloxane (PDMS) microchannel, MPIV measurements revealed a near-plug-like velocity profile, distinct from the parabolic profile of pressure-driven flows [89]. The bulk fluid velocity was found to increase linearly with the applied electric field strength in the streamwise direction (from 5 to 25 kV/m) for certain buffers, though Joule heating can introduce non-linearity [89]. The flow characteristics are highly sensitive to buffer chemistry, including ionic strength and type [89].

Enhancing Mixing in Electroosmotic Micromixers

Electroosmotic micromixers use an applied electric field to actively enhance mixing, which is inherently challenging at the microscale due to low Reynolds numbers. Recent research has focused on optimizing mixer geometry and operating parameters:

• Geometric Optimization: A study using the Taguchi method and Response Surface Methodology (RSM) optimized an electro-osmotic micromixer with two rigid baffles at the entrance. The optimized design (e.g., baffle angles of 146.1° and 82.88°) improved the mixing index by 10.58% compared to the initial design [90]. The inclusion of baffles alone enhanced mixing by 8% through the generation of vortical structures [90].
• Operating Parameters: For the same optimized mixer, increasing the applied voltage from 1 V to 3 V resulted in an average 27% enhancement of the mixing index [90]. Furthermore, applying a phase lag of ( \pi/2 ) to the alternating current (AC) achieved a maximum mixing index of 99.37%, an average 20.1% improvement over using no phase lag [90].
• Ion-Partitioning Effects: In micromixers with a soft polyelectrolyte layer (PEL), the ion-partitioning effect—where ions distribute between the PEL and bulk fluid due to a permittivity difference—can significantly enhance mixing, especially for non-Newtonian fluids. This effect can create an electrical body force an order of magnitude higher than in its absence, leading to stronger flow recirculation and mixing efficiency exceeding 90% at lower permittivity ratios [91].
• Hybrid Nanofluids: The thermal and flow behavior of EOF can be further modulated using hybrid nanofluids. For instance, a mixture of magnesium oxide (MgO) and molybdenum disulfide (MoSâ‚‚) nanoparticles in a base fluid, under electroosmotic forcing and ciliary motion, showed a 33.2% enhancement in axial velocity with an increase in the electroosmotic velocity parameter [92].

Coupling with Pressure-Driven Flow

The interaction between EOF and pressure-driven flow (PDF) is common in microfluidic systems but can adversely affect processes like electrophoretic separation. Numerical simulations show that a PDF opposing the EOF (at Reynolds numbers, Re, from 0.1 to 10) generates a backpressure that distorts sample bands and reduces separation quality [93]. This deformation could not be fully counteracted by simply increasing the applied voltage. A solution involves incorporating a porous polymer plug (pores <5 μm) in the EOF channel, which provides high flow resistance to neutralize the outlet pressure while allowing electromigration. This setup maintained sample integrity and significantly reduced band dispersion for Re ≤ 5 [93].

The Scientist's Toolkit: Essential Reagents and Materials

Table 3: Key Research Reagents and Materials

Item	Function / Application	Specific Examples / Details
High-Entropy Alloy (HEA) Targets	Sputtering source for deposition of diffusion barrier films [87] [88]	Equimolar AlCrTaTiZr [87] [88]
Buffers & Electrolytes	Establish ionic strength and pH for electrokinetic experiments [89]	TAE, TBE, NaCl, Borate Buffer [89]
Fluorescent Particles	Flow seeding for Microparticle Image Velocimetry (MPIV) [89]	-
Hybrid Nanofluids (HNFs)	Enhance thermal and flow properties in microfluidic actuators [92]	MgO and MoSâ‚‚ nanoparticles in base fluid [92]
Polyelectrolyte Layer (PEL)	Modulate ion-partitioning and flow in soft microchannels [91]	Patterned soft layer on microchannel wall [91]
Polymer Monomers	In-situ fabrication of porous plugs for flow control [93]	Ethylene glycol dimethacrylate (EDMA), Glycidyl methacrylate (GMA) [93]

This comparison guide underscores the necessity of a rigorous, multi-faceted approach to quantifying errors in diffusion barriers and electroosmotic flow. Key findings indicate that while computational force fields like Bouhadja's show superior performance for dynamic properties in oxide melts, their predictions can vary significantly, necessitating experimental validation. Quantitatively, AlCrTaTiZrN HEA-N barriers outperform traditional TiN by a factor of 30 in blocking iron diffusion. In electroosmotics, optimized mixer geometries and active control parameters can achieve mixing indices over 99%. The integration of advanced experimental techniques like MPIV and SIMS with carefully benchmarked simulations provides the most robust framework for advancing research in drug development, materials science, and microfluidic technology.

In molecular dynamics (MD), accurately simulating properties that evolve over long timescales—such as viscosity, diffusivity, and electrical conductivity—remains a formidable challenge. While force fields are often parameterized and validated against equilibrium structural properties like density or radial distribution functions, their performance in predicting dynamic transport properties is frequently less rigorous. This gap is critical because many industrial and biological processes, from electrolyte dynamics in batteries to protein-ligand recognition, depend on these non-equilibrium phenomena. Transport properties are exceptionally sensitive to the subtle balance of interatomic forces and the accurate representation of the energy landscape. A force field that excels in predicting the structure of a system can still fail to capture its dynamics, leading to inaccurate predictions in practical applications. This guide provides a systematic framework for benchmarking force fields against transport properties and collective phenomena, offering a comparative analysis of current methodologies to help researchers select and develop models that are truly predictive beyond mere equilibrium.

Force Field Comparison: Performance Across System Types

The accuracy of a force field is highly dependent on the system and properties it was designed to model. The table below summarizes the performance and key characteristics of several force fields as highlighted in benchmarking studies.

Table 1: Comparison of Force Fields for Transport and Equilibrium Properties

Force Field Name / Approach	System Type	Key Strengths	Key Weaknesses / Challenges
Bouhadja et al. [2]	CaO–Al₂O₃–SiO₂ oxide melts	Best agreement with AIMD for Al–O/Ca–O bonding; accurately predicts activation energies and electrical conductivity [2].	Original parameterization may have limited compositional range [2].
Matsui & Guillot [2]	CaO–Al₂O₃–SiO₂ oxide melts	Accurately reproduces densities and Si–O tetrahedral environments [2].	Less accurate for dynamic properties and Al–O/Ca–O bonding compared to Bouhadja [2].
CombiFF [94]	Organic molecules (e.g., haloalkanes, O/N functional groups)	Good agreement with experiment for liquid density, vaporization enthalpy, and solvation properties [94].	Larger discrepancies for shear viscosity and dielectric permittivity (limitation of united-atom, non-polarizable models) [94].
AUA4 (Orozco et al.) [95]	Primary amines (linear, branched, bifunctional)	Transferable for both equilibrium (density, vapor pressure) and transport (shear viscosity) properties [95].	Limited to amine functionalities; performance in mixed-systems uncertain.
Machine Learned (GAP) [36]	EC:EMC battery electrolyte solvent	Targets ab initio (PBE-D2) accuracy; can capture complex intermolecular interactions without predefined separation of scales [36].	Requires complex iterative training; prone to instability (e.g., density collapse in NPT) without careful protocol [36].

Benchmarking Methodologies: Protocols for Validating Transport Properties

A robust benchmarking protocol must go beyond single-point structural validation. The methodologies below are essential for assessing performance on long-timescale phenomena.

Classical Force Field Benchmarking for Oxide Melts

A systematic benchmark of force fields for CaO–Al₂O₃–SiO₂ melts provides a template for rigorous validation [2].

• Simulation Setup: Classical MD simulations are performed across a wide range of compositions and temperatures (e.g., 1400 to 1600 °C). Typical force fields like those of Matsui, Guillot, and Bouhadja use Born-Mayer-Huggins or Buckingham potentials [2].
• Structural Validation: Properties like density, bond lengths (T–O, Al–O, Ca–O), and coordination numbers are calculated and compared against experimental data and ab initio MD (AIMD) simulations [2].
• Transport Property Validation: Key dynamic properties include:
  • Self-diffusion coefficients for network formers and modifiers.
  • Electrical conductivity, calculated via the Einstein relation, which incorporates the cross-correlations between the motions of different ions for accurate prediction [2].
• Performance Metrics: The force field's accuracy is assessed by calculating the deviation from experimental values and its ability to reproduce activation energies for transport [2].

Machine Learning Force Field Development for Molecular Liquids

Developing a Gaussian Approximation Potential (GAP) for an ethylene carbonate/ethyl methyl carbonate (EC:EMC) electrolyte solvent highlights the unique challenges for ML-based methods [36].

• Target Properties: The primary goal is to generate stable dynamics in the NPT ensemble and correctly predict the density, which is highly sensitive to weak intermolecular interactions [36].
• Iterative Training Protocol:
  • Initial Sampling: An initial training set is generated using a classical force field (e.g., OPLS) at various densities and temperatures [36].
  • DFT Labels: Energies, forces, and virials for these configurations are recomputed using a reference quantum-mechanical method (e.g., PBE-D2) [36].
  • Model Fitting & Failure Detection: A GAP model is fitted. Its failure modes in NPT simulation (e.g., unphysical density collapse) are analyzed [36].
  • Active Learning: Unphysical configurations from the failed trajectories are added to the training set to improve the model's robustness iteratively [36].
• Specialized Training Data: The training set is augmented with isolated molecules and rigid-molecule volume scans to ensure a proper balance between intra- and inter-molecular interactions [36].

A Standardized Benchmarking Framework Using Enhanced Sampling

A modular benchmarking framework addresses the need for standardized evaluation across MD methods, particularly for proteins [96].

• Ground Truth Data: The benchmark uses a dataset of nine diverse proteins (e.g., Chignolin, WW domain, λ-repressor). Extensive MD simulations with explicit solvent (AMBER14/TIP3P-FB) are run from multiple starting points to map conformational space [96].
• Enhanced Sampling Core: The benchmark uses the Weighted Ensemble Simulation Toolkit with Parallelization and Analysis (WESTPA) to efficiently sample rare events and conformational states [96].
• Progress Coordinate: A progress coordinate derived from Time-lagged Independent Component Analysis (TICA) guides the weighted ensemble sampling [96].
• Comprehensive Metrics: The framework evaluates methods using over 19 metrics, including:
  • Structural Fidelity: RMSD, contact map differences.
  • Slow-mode Accuracy: TICA energy landscapes.
  • Statistical Consistency: Wasserstein-1 and Kullback-Leibler divergences for distributions of radius of gyration, bond lengths, angles, and dihedrals [96].

The following workflow diagram illustrates the core steps of this standardized benchmarking process:

Figure 1: Standardized Benchmarking Workflow.

The Scientist's Toolkit: Essential Reagents and Computational Tools

Table 2: Key Research Reagents and Computational Tools

Tool / Resource	Function in Validation	Relevant Context / Example
WESTPA [96]	A weighted ensemble simulation toolkit for enhanced sampling of rare events and thorough exploration of conformational space.	Used in standardized benchmarks to compare sampling efficiency of different MD methods [96].
OpenMM [96]	A high-performance simulation toolkit used for running MD simulations with various force fields.	Used to generate ground truth data with AMBER14/TIP3P-FB force field and water model [96].
Gaussian Approximation Potential (GAP) [36]	A machine-learning framework for creating interatomic potentials that aim for ab initio accuracy.	Used to develop a force field for EC:EMC battery electrolyte solvent [36].
SOAP Descriptors [36]	(Smooth Overlap of Atomic Positions) - A mathematical framework to describe atomic environments, used as input for ML potentials like GAP.	Core component of the GAP model for the EC:EMC system [36].
ENERGY STAR Portfolio Manager [97]	A software tool for tracking and benchmarking real-world building energy consumption.	Mandated by Montgomery County and Maryland for building energy performance benchmarking, a real-world analog to computational validation [97] [98].
Hydrogen Mass Repartitioning (HMR) [99]	A numerical technique that allows for longer MD time steps by repartitioning mass from heavy atoms to bonded hydrogens.	Note: Can retard ligand recognition kinetics in protein-ligand simulations, defeating the purpose of performance gains [99].

The rigorous benchmarking of force fields for transport properties is no longer a niche pursuit but a central requirement for reliable molecular simulation. As demonstrated, a force field's excellence in predicting static structure does not guarantee accurate dynamics. The comparative data shows that force fields like Bouhadja's for oxide melts or transferable parameterizations like AUA4 for amines set a high standard by being validated against both equilibrium and transport properties [2] [95]. Meanwhile, ML potentials offer a path to quantum-mechanical accuracy but demand sophisticated, iterative training protocols to avoid catastrophic failures in predicting basic thermodynamic properties like density [36].

The future of force field validation lies in the adoption of standardized, community-wide benchmarks that leverage enhanced sampling techniques, as exemplified by the weighted ensemble framework [96]. These approaches enable fair, reproducible, and comprehensive comparisons between classical, machine-learned, and emerging models. As the field progresses, the integration of these rigorous validation protocols into the development cycle will be crucial for creating the next generation of force fields capable of faithfully simulating the complex, non-equilibrium phenomena that underpin real-world applications in material science, chemistry, and drug discovery.

Assessing Transferability Across Compositions and Temperature Ranges

The accuracy of molecular dynamics (MD) simulations is fundamentally tied to the transferability of the force fields (FFs) employed—their ability to produce reliable predictions across diverse chemical compositions, thermodynamic states, and for a variety of physical properties. As computational methods play an increasingly critical role in fields ranging from drug development to polymer science, benchmarking FF transferability has become essential. A force field that performs excellently for one class of molecules at a specific temperature may fail dramatically when applied to another system or at a different state point. This guide provides a comparative analysis of FF performance, focusing on two key axes of transferability: across varying chemical compositions and over wide temperature ranges. We synthesize findings from recent benchmark studies to offer researchers a clearer understanding of how to select and validate force fields for their specific applications, particularly when accurate prediction of transport properties is required.

Force Field Performance Across Different Chemical Compositions

Benchmarking in Polyamide Membrane Systems

The selection of an appropriate force field is critical for simulating complex molecular systems such as polyamide (PA)-based reverse-osmosis membranes. A comprehensive study evaluated eleven different forcefield-water combinations for simulating cross-linked polyamide membranes formed by trimesoyl chloride (TMC) and m-phenylenediamine (MPD) [46]. The research assessed PCFF, CVFF, SwissParam, CGenFF, GAFF, and DREIDING force fields in combination with different water models (PCFF water, TIP3P, and TIP4P) across multiple states and conditions [46].

Table 1: Performance of Force Fields for Polyamide Membrane Simulations

Force Field	Dry State Density	Hydrated State Properties	Water Permeability	Young's Modulus
CVFF	Accurate prediction	Accurate	Validated at 100 bar	Accurate prediction
SwissParam	Accurate prediction	Accurate	Validated at 100 bar	Accurate prediction
CGenFF	Accurate prediction	Accurate	Validated at 100 bar	Accurate prediction
GAFF	Variable performance	Moderate	Less accurate	Less accurate
PCFF	Variable performance	Moderate	Less accurate	Less accurate
DREIDING	Least accurate	Least accurate	Not accurate	Not accurate

The benchmarking revealed that CVFF, SwissParam, and CGenFF force fields provided the most accurate predictions for dry density, porosity, pore size, and Young's modulus compared to experimental data [46]. These same force fields also successfully predicted pure water permeability within experimental confidence intervals at relevant pressures of 100 bar [46]. The study emphasized that generalized force fields or those determined solely using density functional theory (DFT) cannot guarantee accuracy without systematic validation against experiments with similar chemical composition [46].

Performance in Polymer Electrolytes and Silicone Polymers

Beyond polyamide systems, FF transferability challenges persist in other specialized materials. A benchmark study of classical MD simulations for screening lithium polymer electrolytes highlighted that inaccuracies in modeling polymer glass-transition temperature significantly impact the prediction of ion transport properties [30]. Similarly, for polydimethylsiloxane (PDMS), a comprehensive FF benchmark revealed substantial variations in predicting key thermophysical properties including density, heat capacities, isothermal compressibility, viscosity, and thermal conductivity across different force fields [100].

These studies consistently demonstrate that force fields parameterized for specific chemical groups may lack transferability to structurally distinct systems. For instance, the DREIDING force field, which uses simplified atom typing rules, showed the least accuracy for polyamide membranes [46], while specialized parameterization strategies were necessary for achieving accuracy in silicone polymers [101].

Temperature Transferability of Force Fields

Fundamental Challenges and Limitations

Temperature transferability presents a distinct challenge in molecular simulations. Traditional temperature-agnostic force fields are parameterized at, or near, ambient conditions and are commonly applied across broad temperature ranges [102]. While these FFs work surprisingly well for many applications involving conformational transitions, they systematically underestimate intermolecular dispersion interactions at elevated temperatures [103]. Analysis reveals that this inaccuracy stems partially from changes in molecular polarizability, but primarily from the reduced dielectric constant of the bulk liquid as density decreases with increasing temperature [103].

The failure of certain water models to reproduce phase transition behavior illustrates the limitations of temperature-agnostic FFs. For example, the TIP-3P water model fails to freeze even at low temperatures, leading to the development of specialized models like TIP-4P-ICE that was specifically parameterized to reproduce ice structure [102]. Similarly, the SPC/E water model freezes at -58°C and boils at 123°C, deviating significantly from experimental values [102].

Advanced Approaches for Temperature Transferability

Several sophisticated methods have been developed to address temperature transferability challenges:

Table 2: Approaches for Enhancing Temperature Transferability

Method	Key Principle	Application Examples	Performance
Temperature-Dependent Dispersion Parameters	Establishing dispersion parameter as a linear function of temperature	Molecular liquids (alkane, aromatic, ether, ketone-aldehyde)	Improved prediction of density, heat of vaporization, heat capacity, viscosity across temperatures [103]
Energy Renormalization (ER)	Compensating entropy differences between AA and CG models by parameterizing cohesive energy parameter ε as a function of temperature	Polydimethylsiloxane (PDMS), molecular glass formers, linear-chain polymers	Faithfully preserves dynamics, mechanical and conformational behaviors from glassy to melt regimes [101]
Multistate Parameterization	Systematic generation of different sets of CG potentials at different temperatures followed by fitting	Polyisoprene (PI), Polystyrene (PS)	Enables transferability across wide temperature ranges (e.g., 150K-750K) [104]
Machine Learning-Optimized Coarse-Graining	Using Particle Swarm Optimization with ML models to determine optimal CG potential parameters	Cis-1,4-polyisoprene	Maintains structural and thermodynamic consistency over 150K-750K range [104]

The energy renormalization approach, in particular, has demonstrated remarkable success for silicone polymers. By introducing temperature-dependent factors to renormalize effective distance and cohesive energy parameters, this method enables coarse-grained models to accurately capture glass transition temperature, conformational behaviors, and modulus of elasticity across wide temperature ranges [101].

Experimental Protocols for Benchmarking Studies

Standard Force Field Assessment Methodology

A comprehensive benchmark for polyamide membranes followed this multi-stage protocol [46]:

• Membrane Preparation: Cross-linked PA membranes are prepared with a multi-step process emulating 3D-printed membranes using target density of 1.3 g/cc. The system undergoes energy minimization and multiple simulated-annealing steps to optimize initial geometry, followed by cross-linking under canonical ensemble (NVT) conditions.
• Composition Validation: The chemical composition (O/N ratio, proportions of O and N species) of simulated membranes is validated against experimentally synthesized polyamide membranes with similar chemical compositions.
• Equilibrium MD Simulations: Force fields are evaluated in both dry and hydrated states using equilibrium MD (EMD) simulations to predict properties including density, porosity, pore size distribution, and Young's modulus.
• Non-Equilibrium MD Simulations: Pure water permeation characteristics are assessed at ultra-high feed pressures (0.3–1.5 kbar) using non-equilibrium MD (NEMD) simulations.
• Validation: The most accurate force fields are further utilized to understand pure water permeation mechanisms at experimentally relevant high feed pressures (0.03–0.2 kbar) and seawater desalination conditions.

Temperature Transferability Assessment Protocol

Benchmarking temperature transferability typically involves this systematic approach [104] [103]:

• Multi-State Sampling: Simulations are performed across a broad temperature range (e.g., 150K to 750K) encompassing glassy, transition, and melt regimes.
• Property Calculation: Key properties are calculated at each state point, including:
  • Structural properties: Radial distribution function (RDF)
  • Thermodynamic properties: Density, heat of vaporization, isobaric heat capacity
  • Transport properties: Shear viscosity, thermal conductivity
  • Mechanical properties: Young's modulus, cohesive energy density
• Comparison Metrics: Results are compared against either experimental data or target all-atomistic simulations using metrics such as Debye-Waller factor 〈u²〉 for dynamic consistency and density for thermodynamic consistency.
• Parameter Optimization: For advanced methods, temperature-dependent parameters are optimized using algorithms like Particle Swarm Optimization (PSO) to minimize deviation between simulated and target properties across all state points.

Comparative Analysis of Force Field Performance

Quantitative Comparison Across Multiple Studies

Table 3: Comprehensive Force Field Performance Across Systems and Temperatures

Force Field	Composition Transferability	Temperature Transferability	Best Application Areas	Key Limitations
CVFF	Excellent for polyamide membranes [46]	Limited data	Polyamide membranes, structural properties	May lack cross-correlation terms in bonded interactions [46]
CGenFF	Excellent for polyamide membranes [46]	Limited data	Biomolecular systems, polyamide membranes	Parameterization focused on biological molecules
SwissParam	Excellent for polyamide membranes [46]	Limited data	Diverse organic systems	Relies on topology matching from reference FFs
GAFF	Variable performance across systems [46] [30]	Moderate with corrections	Organic molecules, drug-like compounds	May require validation for specific compositions
DREIDING	Lower accuracy in polyamides [46]	Poor without modification	Initial screening, non-critical applications	Simplified atom typing reduces accuracy
TraPPE	Good for CHâ‚„ and COâ‚‚ [105]	Good with temperature correction	Small molecules, vapor-liquid equilibria	Limited for complex polymers
Energy Renormalization CG	Good for specific polymer classes [101]	Excellent across wide ranges	Polymer systems, glass transition studies	Requires specialized parameterization

Performance in Predicting Transport Properties

Transport properties present particular challenges for force field transferability. The benchmark of polymer electrolytes for Li-ion batteries revealed that inaccuracies in modeling glass-transition temperature directly carry over to errors in predicting ion transport properties [30]. Similarly, for polyamide membranes, only the best-performing force fields could accurately predict experimental pure water permeability within confidence intervals [46].

For viscosity and thermal conductivity prediction, the polydimethylsiloxane benchmark found that existing force fields showed significant discrepancies with experimental measurements, highlighting the need for further development specifically targeting transport properties [100].

Research Reagent Solutions and Computational Tools

Essential Tools for Force Field Benchmarking

Table 4: Key Research Reagents and Computational Tools

Tool/Reagent	Function	Application in Benchmarking
AutoDock Tools	Molecular docking and visualization	Binding pose prediction and analysis [106]
CHARMM General Force Field	All-atom force field for diverse molecules	Comparison of biomolecules and synthetic polymers [46]
GAFF	General Amber Force Field	Broad-spectrum organic molecule simulation [46]
PCFF	Polymer-consistent force field	Specialized for organic polymers [46]
SwissParam	Force field parameterization service	Generating parameters for drug-like molecules [46]
TIP3P/TIP4P Water Models	Solvent representation	Hydration effects in membrane systems [46]
LAMMPS/GROMACS	Molecular dynamics engines	Running equilibrium and non-equilibrium MD simulations [46] [101]
Particle Swarm Optimization	Parameter optimization algorithm	Determining optimal CG potential parameters [104]
SiriusT3	Physicochemical property analysis	Experimental validation of solubility and lipophilicity [107]

The transferability of force fields across compositions and temperature ranges remains a significant challenge in molecular simulations. Benchmark studies consistently show that force field performance is highly system-dependent, with CVFF, SwissParam, and CGenFF demonstrating superior accuracy for polyamide membrane systems, while specialized approaches like Energy Renormalization and machine learning-optimized coarse-graining offer promising solutions for temperature transferability.

For researchers seeking to simulate novel systems, our analysis recommends: (1) prioritizing force fields with proven performance for chemically similar systems, (2) implementing temperature-dependent parameter corrections when studying broad temperature ranges, (3) validating against multiple property types (structural, thermodynamic, and transport), and (4) considering emerging machine-learning approaches for the most challenging transferability problems. As force field development continues to advance, the integration of data-driven methods with physical principles holds particular promise for achieving the long-sought goal of universally transferable force fields.

Conclusion

Benchmarking force fields for transport properties is not a one-size-fits-all endeavor but a critical, system-dependent process. This synthesis demonstrates that while classical force fields offer computational efficiency, they often fail to capture key dynamic phenomena, with different potentials yielding quantitatively and sometimes qualitatively different results. The emergence of machine-learned force fields and sophisticated optimization frameworks presents a paradigm shift, offering a path to quantum accuracy at classical computational cost. For biomedical research, this progress is pivotal, enabling more reliable predictions of drug diffusion, biomolecular interactions, and electrolyte behavior. Future directions must focus on developing standardized benchmarking datasets, improving the data efficiency of ML potential training, and creating more transferable models that faithfully capture both structural and kinetic properties across the diverse chemical space relevant to drug development and biological systems.

References

• 1. A Comparison of Classical Force-Fields for Molecular ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC5509262/]
• 2. Molecular dynamics studies of the structural and transport ... [https://www.sciencedirect.com/science/article/abs/pii/S0927025625004938]
• 3. Comparison of structural, thermodynamic, kinetic and mass ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4409555/]
• 4. Comparative Study of Molecular Mechanics Force Fields for β ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10302482/]
• 5. Force field comparison for molecular dynamics simulations ... [https://www.sciencedirect.com/science/article/abs/pii/S0167732224024061]
• 6. Evaluating Universal Machine Learning Force Fields ... [https://arxiv.org/html/2508.05762v1]
• 7. Modeling the potential energy surface by force fields for ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d5sc02715b?page=search]
• 8. High-speed and low-power molecular dynamics processing unit... [https://www.nature.com/articles/s41524-024-01422-3?error=cookies_not_supported&code=345c5ec5-a966-43fd-ac50-6618099d5034]
• 9. Multiscale Free Energy Simulations: An Efficient Method for ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3985817/]
• 10. Force-Field Benchmark for Polydimethylsiloxane: Density, ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11831649/]
• 11. Scaling Molecular Dynamics with ab initio Accuracy to 149 ... [https://arxiv.org/html/2410.22867v1]
• 12. Benchmarking of classical force fields by ab initio ... [https://www.sciencedirect.com/science/article/abs/pii/S2210271X13002715]
• 13. Molecular dynamics studies of the structural and transport ... [https://biblio.ugent.be/publication/01K228AMKPD30PXN737NMECTQ3]
• 14. Comparison among Amber-ff14SB, Amber-ff19SB, and ... [https://pubmed.ncbi.nlm.nih.gov/41233298/]
• 15. On the Physical Origins of Reduced Ionic Conductivity in ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11984311/]
• 16. Addressing pathological deficiencies in the simulation of ... [https://www.nature.com/articles/s41598-025-04482-7]
• 17. APEX: an automated cloud-native material property explorer [https://www.nature.com/articles/s41524-025-01580-y]
• 18. LAMMPS and GROMACS give very different Potential of ... [https://matsci.org/t/lammps-and-gromacs-give-very-different-potential-of-mean-force-with-plumed/60511]
• 19. Coarse-grained models for ionic liquids and applications to ... [https://pubs.rsc.org/en/content/articlehtml/2025/im/d5im00021a]
• 20. A Review of Ionic Liquids and Their Composites with ... [https://www.mdpi.com/2304-6740/12/7/186]
• 21. Accurate machine learning force fields via experimental ... [https://www.nature.com/articles/s41524-024-01251-4]
• 22. Choice of Force Field for Proteins Containing Structured and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC7136338/]
• 23. Biological nanopores for single-molecule sensing - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC9014393/]
• 24. Systematic Validation of Protein Force Fields against ... [https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0032131]
• 25. Evaluating the Performance of the ff99SB Force Field Based ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC2718158/]
• 26. Migration Pathways as Diagnostic Probes: Benchmarking and... [https://arxiv.org/html/2509.00090v1]
• 27. Evaluating Universal Machine Learning Force Fields ... [https://arxiv.org/abs/2508.05762]
• 28. Charge Scaling in Classical Force Fields for Lithium Ions ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC11483941/]
• 29. Dynamic bonds transform ion transport mechanisms in ... [https://pubs.rsc.org/en/content/articlehtml/2025/mh/d5mh00433k]
• 30. Benchmarking Classical Molecular Dynamics Simulations ... [https://chemrxiv.org/engage/chemrxiv/article-details/67f445e1fa469535b92cad31]
• 31. A materials discovery framework based on conditional generative... [https://pubs.rsc.org/en/content/articlehtml/2025/dd/d4dd00293h]
• 32. Article Unlocking high lithium-ion transport in solid polymer ... [https://www.sciencedirect.com/science/article/pii/S2666386425002231]
• 33. Insight into Properties and Structures of Ionic Liquids by ... [https://www.sciencedirect.com/science/article/pii/S2468025725001645]
• 34. Addressing pathological deficiencies in the simulation of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12215625/]
• 35. EMFF-2025: a general neural network potential for ... [https://www.nature.com/articles/s41524-025-01809-w]
• 36. Machine learning force fields for molecular liquids [https://www.nature.com/articles/s41524-023-01100-w]
• 37. Egret-1: Pretrained Neural Network Potentials for Efficient and ... [https://www.rowansci.com/publications/egret-1-pretrained-neural-network-potentials]
• 38. Uncovering ion transport mechanisms in ionic liquids using ... [https://pubs.rsc.org/en/content/articlehtml/2025/dd/d4dd00378k]
• 39. Comparison among Amber-ff14SB, Amber-ff19SB, and ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC12659023/]
• 40. CHARMM additive and polarizable force fields for biophysics ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC4334745/]
• 41. Alternating current electrohydrodynamics in microsystems [https://pmc.ncbi.nlm.nih.gov/articles/PMC4676781/]
• 42. CHARMM | CHARMM [https://academiccharmm.org/]
• 43. Migration as a Probe: A Generalizable Benchmark ... [https://arxiv.org/html/2509.00090v2]
• 44. Migration as a Probe: A Generalizable Benchmark ... [https://chatpaper.com/paper/185705]
• 45. Molecular dynamics simulation for all - PMC - PubMed Central [https://pmc.ncbi.nlm.nih.gov/articles/PMC6209097/]
• 46. Benchmarking forcefields for molecular dynamics ... [https://www.sciencedirect.com/science/article/abs/pii/S0376738824010871]
• 47. An active learning force field for the thermal transport ... [https://pubs.rsc.org/en/content/articlelanding/2025/cp/d5cp00232j]
• 48. T020 · Analyzing molecular dynamics simulations [https://projects.volkamerlab.org/teachopencadd/talktorials/T020_md_analysis.html]
• 49. New computational chemistry techniques accelerate the ... [https://news.mit.edu/2025/new-computational-chemistry-techniques-accelerate-prediction-molecules-materials-0114]
• 50. Quality Control of Quantitative High Throughput Screening ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC6520559/]
• 51. A systematic fitting procedure for accurate force field ... [https://www.sciencedirect.com/science/article/abs/pii/S0010465515003999]
• 52. The PHAST 2.0 Force Field for General Small Molecule ... [https://pubmed.ncbi.nlm.nih.gov/40459410/]
• 53. Supplemental: Overview of the Common Force Fields [https://computecanada.github.io/molmodsim-md-theory-lesson-novice/S01-Force_Fields_Overview/index.html]
• 54. How the CADD Center Accelerates Drug Design [https://news.pharmacy.umaryland.edu/how-the-cadd-center-accelerates-drug-design/]
• 55. FEP in 2025: We're Going to Need a Bigger Drug Discovery ... [https://cresset-group.com/science/science-resources/fep-in-2025/]
• 56. Data-driven parametrization of molecular mechanics force ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d4sc06640e]
• 57. Active-Learning Assisted General Framework for Efficient ... [https://pubmed.ncbi.nlm.nih.gov/39999292/]
• 58. Bayesian force fields from active learning for simulation of ... [https://www.nature.com/articles/s41524-021-00510-y]
• 59. Advancing Learning Through Memory-Based Dual Gaussian ... [https://scisimple.com/en/articles/2025-10-29-advancing-learning-through-memory-based-dual-gaussian-processes--a98yrzj]
• 60. Force field - GROMACS 2025-rc documentation [https://manual.gromacs.org/documentation/2025-rc/reference-manual/functions/force-field.html]
• 61. Long-Range Forces and Neural Network Potentials [https://cwagen.substack.com/p/long-range-forces-and-neural-network]
• 62. Long-Range Interactions in High-Dimensional Neural ... [https://chemrxiv.org/engage/chemrxiv/article-details/688a8f0f728bf9025e2d8c6e]
• 63. AIMNet2: a neural network potential to meet your neutral ... [https://pubs.rsc.org/en/content/articlehtml/2025/sc/d4sc08572h]
• 64. Benchmarking OMol25-Trained Models on Experimental ... [https://rowansci.com/publications/omol25-redox]
• 65. Benchmarking Universal Machine Learning Interatomic ... [https://arxiv.org/html/2510.22999v1]
• 66. Evaluating the transferability of machine-learned force ... [https://www.sciencedirect.com/science/article/abs/pii/S0010465523000681]
• 67. Generalist vs. Specialist AI Models [https://www.linkedin.com/pulse/generalist-vs-specialist-ai-models-healthcare-life-sciences-nama-qpyse]
• 68. AI Models Enhance the Drug Discovery Portfolio [https://www.genengnews.com/topics/artificial-intelligence/ai-models-enhance-the-drug-discovery-portfolio/]
• 69. Generalist vs Specialist Time Series Foundation Models [https://www.arxiv.org/abs/2510.14254]
• 70. Foundation models in drug discovery: phenomenal growth ... [https://www.sciencedirect.com/science/article/pii/S1359644625002314]
• 71. E(3)-equivariant graph neural networks for data-efficient ... [https://www.nature.com/articles/s41467-022-29939-5]
• 72. Studying rare events using forward-flux sampling [https://pubmed.ncbi.nlm.nih.gov/32061206/]
• 73. Best Practices for Computing Transport Properties 1. Self ... [https://livecomsjournal.org/index.php/livecoms/article/view/v1i1e6324]
• 74. Kinetics of Barrier Crossing Events from Temperature ... [https://arxiv.org/html/2509.05068v1]
• 75. Benchmarking of force fields to characterize the intrinsically ... [https://www.nature.com/articles/s41598-023-40801-6]
• 76. An artificial intelligence accelerated ab initio molecular ... [https://www.nature.com/articles/s41597-025-05338-5]
• 77. A large-scale on-the-fly machine learning molecular ... [https://www.sciencedirect.com/science/article/abs/pii/S2095495625005479]
• 78. Parameterization and validation of force | Fiveable fields [https://fiveable.me/computational-chemistry/unit-9/parameterization-validation-force-fields/study-guide/LvMzZqIJvjD63P0q]
• 79. Fine-tuning molecular mechanics force fields to experimental ... [https://pubmed.ncbi.nlm.nih.gov/39829785/]
• 80. [2511.20863] Bridging Atomistic and Mesoscale Lithium Transport via... [https://arxiv.org/abs/2511.20863]
• 81. Current Status of the AMOEBA Polarizable Force Field - PMC [https://pmc.ncbi.nlm.nih.gov/articles/PMC2918242/]
• 82. AMOEBA in OpenMM Speed and Accuracy Benchmark [https://simtk.org/projects/openmm-amoeba]
• 83. Forcefield Optimization for Energetic Materials - 3DS Blog [https://blog.3ds.com/brands/biovia/forcefield-optimization-for-energetic-materials/]
• 84. Information-Theoretic Analysis of Selected Water Force ... [https://www.mdpi.com/1099-4300/27/10/1073]
• 85. The COMPASS force field: Validation for carbon nanoribbons [https://www.sciencedirect.com/science/article/abs/pii/S138694771930342X]
• 86. Deep Residual Learning for Molecular Force Fields [https://chemrxiv.org/engage/chemrxiv/article-details/68f04cb3bc2ac3a0e03449c3]
• 87. Diffusion barrier with 30-fold improved performance using ... [https://www.sciencedirect.com/science/article/abs/pii/S0925838819329883]
• 88. Diffusion Barrier Performance of AlCrTaTiZr ... [https://www.mdpi.com/1099-4300/22/2/234]
• 89. Electroosmotic flow velocity measurements in a square ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC3776255/]
• 90. Investigation of mixing performance in electro-osmotic ... [https://www.nature.com/articles/s41598-025-01812-7]
• 91. Ion-partitioning effect promotes the electroosmotic mixing ... [https://pubs.rsc.org/en/content/articlepdf/2025/cp/D5CP02072G]
• 92. Heat transfer enhancement in electroosmotic and ciliary ... [https://www.sciencedirect.com/science/article/pii/S1687850725004765]
• 93. Effect of pressure-driven flow on electroosmotic flow and ... [https://www.sciencedirect.com/science/article/abs/pii/S0017931023000807]
• 94. Force fields optimized against experimental data for large ... [https://www.sciencedirect.com/science/article/pii/S1093326322001917]
• 95. Transferable force field for equilibrium and transport ... [https://pubmed.ncbi.nlm.nih.gov/22034922/]
• 96. A Standardized Benchmark for Machine-Learned ... [https://arxiv.org/html/2510.17187v1]
• 97. Energy Benchmarking Requirements [https://www.montgomerycountymd.gov/DEP/energy/commercial/energy-benchmarking.html]
• 98. Maryland BEPS “Notice of Required Action”: What It Means ... [https://honeydewadvisors.com/maryland-beps-2025-notice-of-required-action/]
• 99. Long-time-step molecular dynamics can retard simulation of ... [https://pmc.ncbi.nlm.nih.gov/articles/PMC10027446/]
• 100. Force-Field Benchmark for Polydimethylsiloxane [https://pubmed.ncbi.nlm.nih.gov/39895120/]
• 101. Energy renormalization for temperature transferable coarse ... [https://pubs.rsc.org/en/content/articlehtml/2024/cp/d3cp05969c]
• 102. Effect of temperature on Forcefield parameters in classical ... [https://mattermodeling.stackexchange.com/questions/11390/effect-of-temperature-on-forcefield-parameters-in-classical-molecular-dynamics-s]
• 103. Temperature Transferability of Force Field Parameters for ... [https://pubmed.ncbi.nlm.nih.gov/29800527/]
• 104. Constructing a temperature transferable coarse-grained ... [https://www.sciencedirect.com/science/article/abs/pii/S0032386124008528]
• 105. Force field comparison and thermodynamic property ... [https://www.sciencedirect.com/science/article/abs/pii/S0378381214000727]
• 106. Frontiers | Flunarizine as a potential repurposed drug for the serotonin... [https://www.frontiersin.org/journals/pharmacology/articles/10.3389/fphar.2025.1599297/full]
• 107. SiriusT3: Physicochemical Property Analysis for Drug ... Development [https://www.aimil.com/blog/physicochemical-property-analysis-for-drug-development-in-india/]